空间站舱体水平旋转装备六点调平算法及同步控制方法

任明妍，谭 旭，曾 婷，王 荣，李海月

（北京卫星制造厂有限公司，北京 100094）

空间站舱体水平旋转装备是在空间站舱体总装过程中用于稳定支撑与调姿的装备，其可以完成空间站舱体在总装厂房内的运输，并可根据总装需要，使空间站舱体以其水平方向中心线为轴进行旋转，以达到理想位置，便于下一步装配。水平旋转装备的长度为10 m，宽度为5 m，负载为30 t。为了保证水平旋转装备的上平面水平，以确保空间站舱体放置在水平旋转装备上后质心稳定以及结构不发生变形，须对水平旋转装备进行调平。

四点调平是目前应用最为广泛的调平方式，其主要通过调节位于设备4个边角处4条螺旋升降支腿的高度来达到调平上平面的目的。Ream等[1]采用2个水平传感器分别感应调平装备水平面对角线方向相对地面的水平度，并通过追逐式调平法进行调平；Parlikar等[2]提出了一种适用于武器系统的四点调平方法，即利用1个倾角传感器将检测到的角度信号反馈至控制器，通过计算4条螺旋升降支腿的位置坐标来控制其升降；高天翔[3]对比了逐高法、逐低法和中心不动法这3种四点调平方法，通过分析发现中心不动法的调平时间最短，但由于4条螺旋升降支腿存在升、降两个方向的移动，调平精度较低，须采用逐高法及主从式控制策略进一步提升液压调平系统的同步控制性能；为了提高调平精度，徐嵩[4]提出了一种用于发射车的六点调平方法，即利用1个倾角传感器通过固定轴翻转法进行调平，该方法能够使发射车运行平稳，并实现快速调平。

但是，上述文献均针对调平装备上平面为刚性的情况。在实际调平实验中，由于空间站舱体较重，而水平旋转装备较长，当空间站舱体放置在水平旋转装备上后，水平旋转装备受到了较大的压力，其在长度方向上产生了轻微的变形。若空间站舱体长期放置在变形的水平旋转装备上，既会严重影响水平旋转装备的使用寿命，也会对空间站舱体结构造成一定的影响。

为解决上述问题，笔者基于现有的空间站舱体水平旋转装备，提出了一种针对非刚性结构的六点调平算法及同步控制方法，旨在实现水平旋转装备的六点自动调平，使其上平面的水平度达到0.001°以内，以确保空间站舱体的质心稳定及结构不发生变形。

1 空间站舱体水平旋转装备六点调平方案

原有的空间站舱体水平旋转装备依靠分布在4个边角处的螺旋升降支腿进行整体升降和稳定支撑。其调平原理为：利用放置在水平旋转装备上平面上的双轴倾角传感器来采集上平面与水平方向以及竖直方向的夹角，以确定最高的螺旋升降支腿，并采用“只升不降”的方法，使其余3条螺旋升降支腿上升，最终实现上平面水平[5-8]。

为解决空间站舱体水平旋转装备负载30 t后会在长度方向上产生变形的问题，在2条长边的中心位置处各增加1条螺旋升降支腿，并在增加的支腿与短边之间分别放置1个双轴倾角传感器S1与1个单轴倾角传感器S2，如图1所示。

图1 空间站舱体水平旋转装备六点调平原理Fig.1 Six-point leveling principle for horizontal rotating equipment of space station cabin

1.1 水平旋转装备控制系统组成

基于六点调平的空间站舱体水平旋转装备控制系统的硬件结构主要由上位机、主控制器、驱动器、电机、角度传感器、双轴倾角传感器以及单轴倾角传感器组成，如图2所示[9-11]。

图2 基于六点调平的空间站舱体水平旋转装备控制系统硬件组成Fig.2 Hardware composition of control system of horizontal rotating equipment of space station cabin based on sixpoint leveling

基于六点调平的空间站舱体水平旋转装备共包含2套翻转机构和6条螺旋升降支腿。其中，2套翻转机构分别放置于装备的左、右两侧，用于驱动空间站舱体翻转，角度传感器1和角度传感器2用于采集装备两侧的翻转角度，以确保翻转的同步性；6个支腿电机分别安装在6条螺旋升降支腿上，负责水平旋转装备的调平。双轴倾角传感器S1位于由螺旋升降支腿1，2，3，4所围成的矩形平面的几何中心处，以采集这4条支腿所围成的矩形平面与水平方向的夹角α1以及与竖直方向的夹角β1；单轴倾角传感器S2位于由螺旋升降支腿3，4，5，6所围成的矩形平面的几何中心处，以采集这4条支腿所围成的矩形平面与水平方向的夹角α2。当主控制器接收到α1、α2、β1这3个角度信号后，通过六点调平模块解算各支腿的升降速度及方向并输出至6个支腿电机驱动器，以驱动电机动作，从而达到调平目的。

定义双轴倾角传感器S1与单轴倾角传感器S2在水平方向上的正方向为从左到右，在竖直方向上的正方向为从前到后。当S1沿水平方向的正方向高于水平线时，α1＞0°，当S1沿水平方向的正方向低于水平线时，α1＜0°；当S2沿水平方向的正方向高于水平线时，α2＞0°，当S2沿水平方向的正方向低于水平线时，α2＜0°；当S1沿竖直方向的正方向高于竖直线时，β1＞0°，当S1沿竖直方向的正方向低于竖直线时，β1＜0°。

1.2 六点调平算法原理

本文所提出的六点调平算法是一种解析计算方法。在实际调平过程中，操作者在上位机中输入空间站舱体水平旋转装备的上升高度，而后上位机将高度参数传输至主控制器，主控制器通过逻辑控制模块将高度参数发送至六点调平模块，最后由六点调平模块控制支腿电机运动。当某一支腿到达给定高度后，进入调平阶段：六点调平模块根据接收到的由双轴倾角传感器S1采集的α1、β1以及单轴倾角传感器S2采集的α2，对6条支腿的当前高度进行排序，并采用“只升不降”方式，计算确定各支腿的上升高度；在给定调平时间T后，使6条支腿在同一时刻完成上升动作，实现六点同步调平[12-14]。

由于β1只对竖直方向的2条支腿的高度存在影响，且2条支腿的高度差为|L1sinβ1|，通过分析α1、α2的大小及方向即可得到因6条支腿高度不同而造成的空间站舱体水平旋转装备上平面的不同姿态：第1类为空间站舱体水平旋转装备支腿1，2，5，6为最高支腿的姿态，其中2种情况如图3(a)和图3(b)所示；第2类为空间站舱体水平旋转装备支腿3，4为最高支腿的姿态，其中支腿3最高的情况如图3(c)所示。

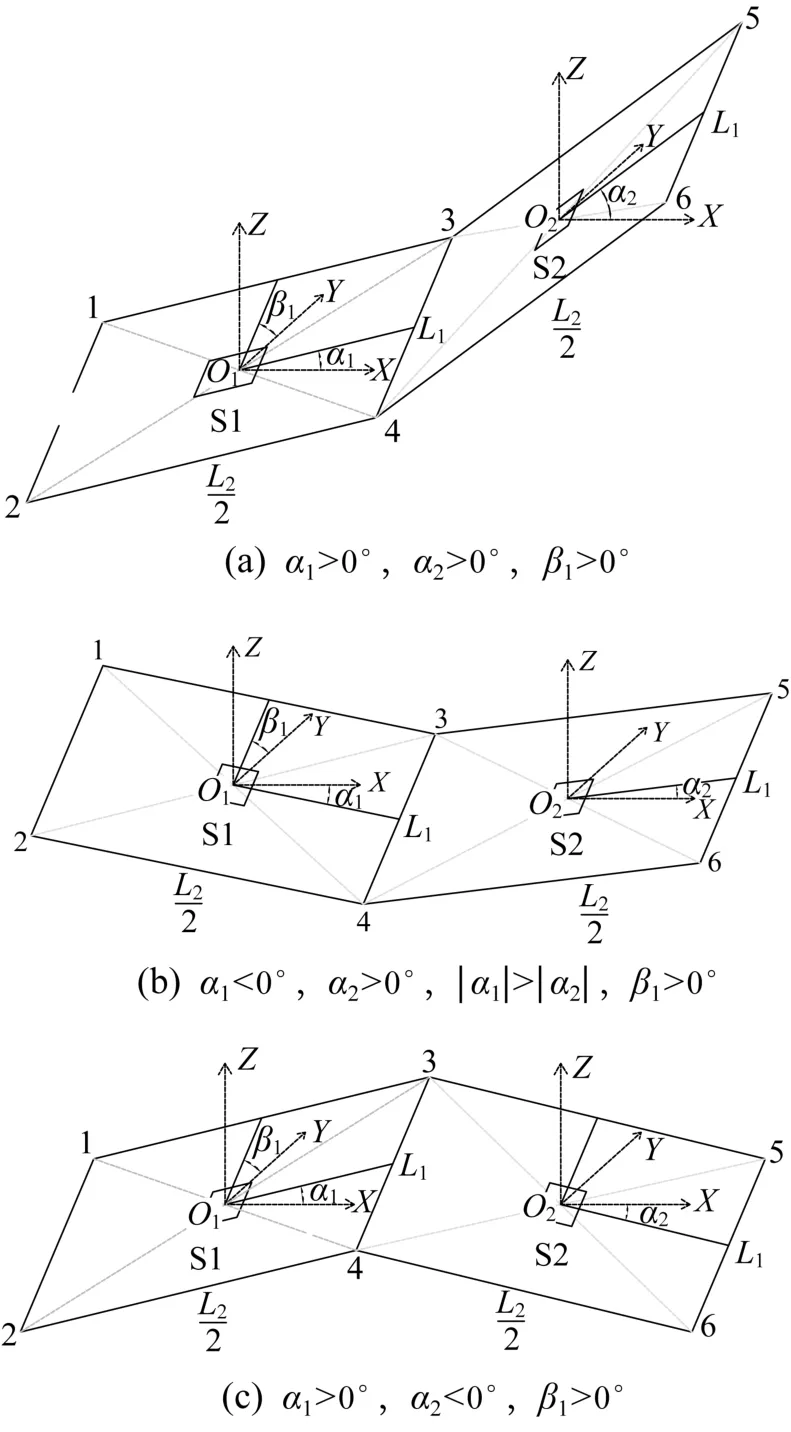
图3 空间站舱体水平旋转装备上平面姿态示意Fig.3 Schematic of upper plane attitude of horizontal rotating equipment of space station cabin

通过分析α1、α2、β1这3个角度的大小和方向，可确定在开始调平前空间站舱体水平旋转装备上平面的角度与最高支腿的关系，如表1所示。

表1 空间站舱体水平旋转装备上平面角度与最高支腿的关系Table 1 Relationship between upper plane angle of horizontal rotating equipment of space station cabin and the highest outrigger

假设空间站舱体水平旋转装备6条支腿的调平加速时间为t0，总调平时间为T；支腿1的加速度为a1，支腿2的加速度为a2，支腿3的加速度为a3，支腿4的加速度为a4，支腿5的加速度为a5，支腿6的加速度为a6；水平旋转装备上平面的长度为L2，宽度为L1。通过计算可得当任意1条支腿最高时，其余支腿的上升高度与对应加速时间的关系。以支腿1最高为例，其余各支腿的上升高度与对应加速时间的关系为：

由表1可知，在不同的空间站舱体水平旋转装备上平面姿态下，6条支腿的高低顺序有多种，但对于不同的最高支腿情况，其调平原理相同，故本文以图3(a)所示姿态（α1＞0°，α2＞0°，β1＞0°，支腿5最高）进行分析。在开始调平后的任意时刻t下，支腿2与支腿4的高度差为：

式中：α10为双轴倾角传感器S1所采集的未开始调平前支腿1，2，3，4所围成的矩形平面与水平方向的夹角。

根据式(2)可得任意时刻t下α1与α10的关系，为：

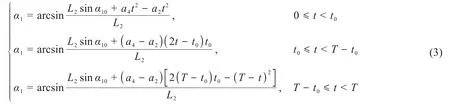
同理，在开始调平后的任意时刻t下，通过分析支腿4与支腿6的高度差即可得单轴倾角传感器S2所采集的α2与未开始调平前的α20的关系，为：

同理，在开始调平后的任意时刻t下，通过分析支腿1与支腿2的高度差即可得出双轴倾角传感器S1所采集的β1与未开始调平前的β10的关系，为：

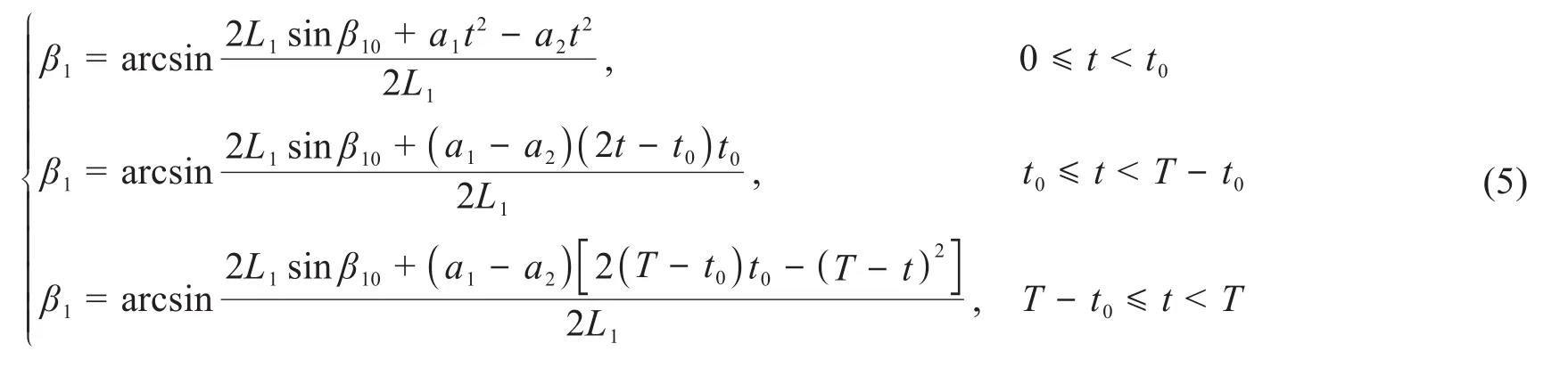
在得到不同时刻下α1与α10、α2与α20以及β1与β10的关系后，通过仿真分析α1、α2和β1随时间的变化趋势。

假设T=20 s，t0=3.1 s，L1=5 m，L2=10 m，α10=0.237°，α20=0.463°，β10=0.265°。通过仿真分析得到支腿5最高时α1、α2、β1这3个角度在开始调平后的变化趋势，结果如图4所示。

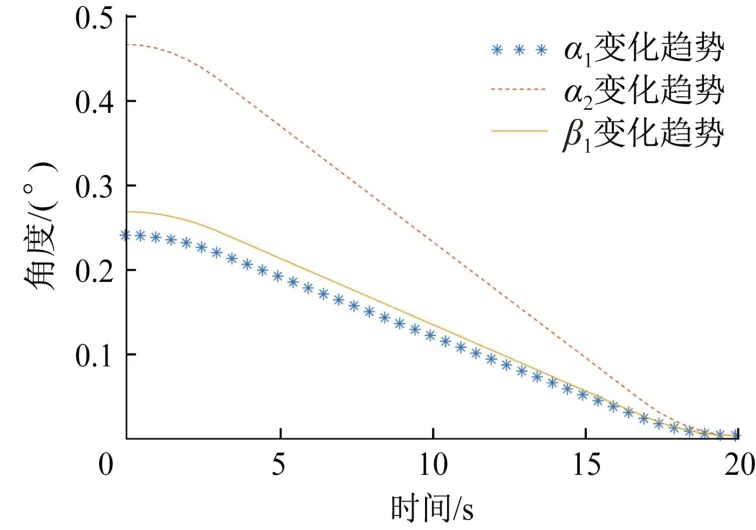
图4 第1类姿态下（支腿5最高）开始调平后α1、α2、β1的变化趋势Fig.4 Changing trend of α1,α2,β1after leveling under the first type of attitude(with the highest outrigger 5)

由图4可知，六点调平算法通过同步控制6条支腿的高度，可使α1、α2、β1这3个角度在调平结束后变为0°，即实现了空间站舱体水平旋转装备的调平。

为验证上述结果的正确性，以表1中第5种情况（α1＞0°，α2＜0°，β1＞0°，支腿3最高）为例，开展仿真分析。

在未开始调平前，空间站舱体水平旋转装备呈现图3(c)所示的第2类姿态，其最高支腿为支腿3。假设α10=0.327°，α20=-0.214°，β10=0.363°，保证总调平时间T和调平加速时间t0不变，通过仿真分析得到α1、α2、β1这3个角度在开始调平后随时间的变化趋势，结果如图5所示。

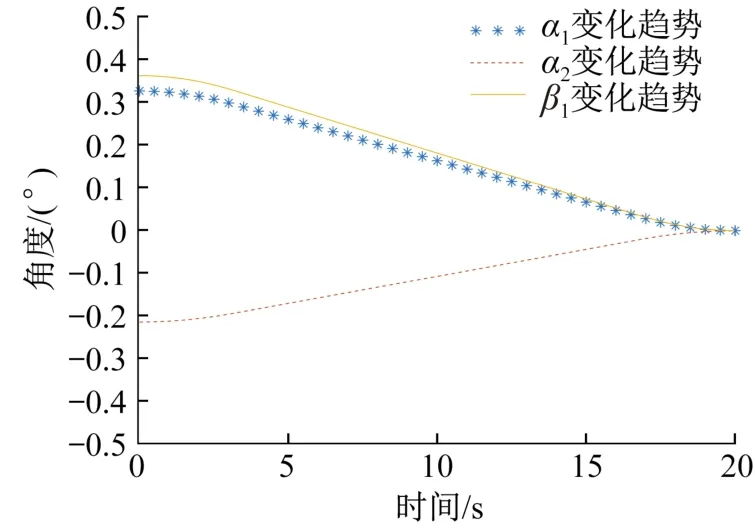
图5 第2类姿态下（支腿3最高）开始调平后α1、α2、β1的变化趋势Fig.5 Changing trend of α1,α2,β1after leveling under the second type of attitude(with the highest outrigger 3)

由图5可以看出，采用所提出的六点调平算法对空间站舱体水平旋转装备进行调平后，α1、α2、β1这3个角度在调平结束后均变为0°，即实现了水平旋转装备的六点同步调平，达到预期效果，验证了所提出算法的可行性。

2 空间站舱体水平旋转装备六点调平同步控制原理

在调平过程中，空间站舱体水平旋转装备各支腿的运动速度、位置相互影响，即存在耦合效应，须对其同步控制原理进行分析，以降低支腿电机同步运动的跟随误差。通过对多电机协同运动控制方法（包括相邻耦合控制、环形耦合控制以及交叉耦合控制等）进行分析后发现，交叉耦合控制方法的耦合关系较为全面，比其他耦合控制方法的运行精度高[15-16]。因此，本文参考交叉耦合同步控制方式，提出了一种基于交叉耦合的六点调平同步控制方法，以保证空间站舱体水平旋转装备上平面的调平精度达到0.001°以内。

基于交叉耦合的六点调平同步控制方法的原理（见图6）为：先通过采集6个支腿电机的转速信号并比较各支腿电机转速的跟随误差，得到同步误差耦合参数；再分别将得到的同步误差耦合参数与各支腿电机的增益系数相乘，得到误差补偿参数，并将其输入误差补偿器，形成误差调整信号，以对各支腿的运动状态作实时调整，从而提高支腿电机的同步性。

图6 基于交叉耦合的六点调平同步控制原理Fig.6 Principle of six-point leveling synchronous control based on cross coupling

以支腿1为例，其同步误差耦合模型如图7所示。

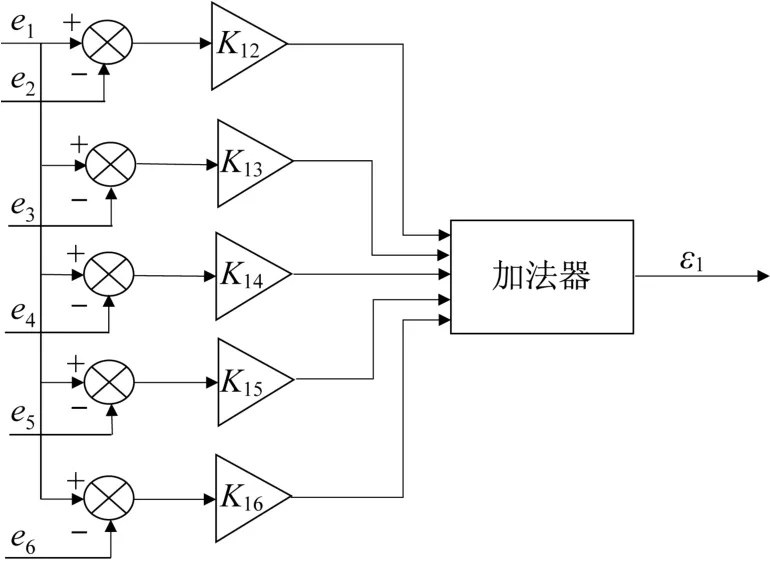
图7 支腿1的同步误差耦合模型Fig.7 Synchronous error coupling model of outrigger 1

由图6和图7可知，支腿i的跟踪误差可表示为：

式中：ni为支腿i电机的实际转速；ni*为支腿i电机在理想状态下的转速。

则支腿i的同步误差εi可表示为：

式中：Kij为支腿i电机与支腿j电机的耦合系数。

3 实验验证

为验证所提出的空间站舱体水平旋转装备的六点调平算法及同步控制方法的正确性，开展同步控制实验以及六点调平实验。实验中所用的空间站舱体水平旋转装备如图8所示。

图8 空间站舱体水平旋转装备实物Fig.8 Physical object of horizontal rotating equipment of space station cabin

3.1 同步控制实验

同步控制实验的目的是验证空间站舱体水平旋转装备的6个支腿电机在升降过程中的同步性。设定6个支腿电机的目标转速为1 000 r/min，分别在未采用/采用交叉耦合同步控制下令支腿电机加速至目标转速，通过采集加速过程中6个支腿电机的实时转速来检测其跟随误差。未采用/采用交叉耦合同步控制下支腿电机的转速曲线如图9所示。

图9结果表明，采用基于交叉耦合的同步控制方法后，6个支腿电机的转速跟随误差从57 ms缩短至8 ms，其同步性得到大幅提升，可为空间站舱体水平旋转装备的六点调平提供较好的同步控制基础。

3.2 六点调平实验

空间站舱体水平旋转装备所采用的双轴倾角传感器S1与单轴倾角传感器S2的分辨率为0.000 5°。将表1所示的10种情况所对应的调平控制方式写入主控制器的六点调平模块。其中，系统默认的总调平时间T=20 s，6条支腿的调平加速时间t0=3.1 s。在初始阶段，在上位机中输入水平旋转装备上平面的上升高度为100 mm后启动。在第1次调平实验中，支腿4先达到100 mm，而后6条支腿停止运动并进入自动调平模式，此时α10=0.186 5°，α20=-0.236 0°，β10=-0.115 0°，通过计算可得6条支腿的加速度 ：a1=0.000 564 m/s，a2=0.000 373 m/s，a3=0.000 192 m/s，a4=0 m/s，a5=0.000 663 m/s，a6=0.000 472 m/s。6条支腿按照设定的加速时间和加速度开始运动。在调平过程中，监测双轴倾角传感器S1与单轴倾角传感器S2所采集的α1、α2、β1这3个角度的变化趋势，结果如图10所示。

图10 第1次调平过程中α1、α2、β1的变化趋势Fig.10 Changing trend of α1, α2and β1during the first leveling process

从图10中可以看出，在第1次调平实验中，α1从0.186 5°变为0.000 7°，α2从-0.236 0°变为0.000 4°，β1从-0.115 0°变为0.000 8°，即水平度小于0.001°，实现了预期目标。经测量，空间站舱体水平旋转装备在长度方向上的最大变形量为0.065 mm，不会影响其使用寿命[17-18]。

在第1次调平完成后，将6条支腿下降至最低，然后进行第2次调平实验，设空间站舱体水平旋转装备上平面的上升高度为80 mm。在本次调平过程中，支腿2先达到80mm，而后6条支腿停止运动并进入自动调平模式，此时α10=-0.375 5°，α20=-0.219 0°，β10=-0.282 5°。在调平过程中，监测双轴倾角传感器S1与单轴倾角传感器S2所采集的α1、α2、β1这3个角度的变化趋势，结果如图11所示。

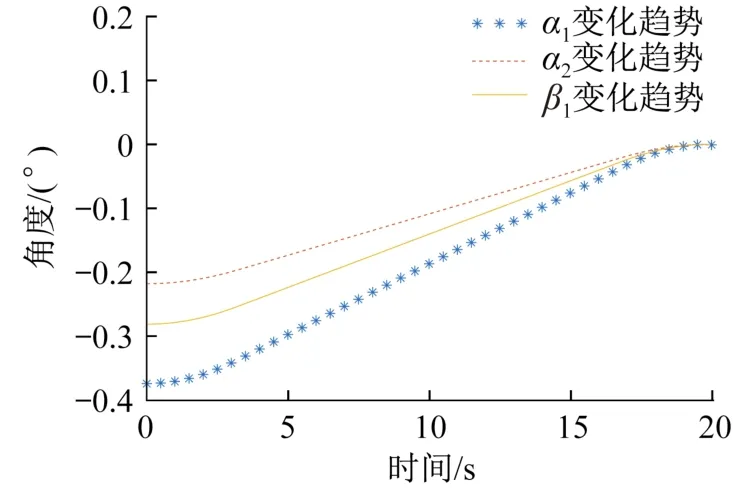
图11 第2次调平过程中α1、α2、β1的变化趋势Fig.11 Changing trend of α1,α2,and β1during the second leveling process

从图11中可以看出，α1从-0.375 5°变化到-0.000 5°，α2从-0.219 0°变化到 0.000 4°，β1从-0.282 5°变化到 0.000 3°，水平度小于0.001°，实现了预期目标。经测量，空间站舱体水平旋转装备在长度方向上的最大变形量为0.044 mm，不会影响其使用寿命。

按照上述实验方法，共开展10次调平实验，结果如表2所示。

表2 每次调平实验后α1、α2、β1的最终值Table 2 Final value of α1, α2,and β1after each leveling experiment

根据表2数据可知，在10次调平实验中，当完成自动调平后，α1、α2、β1这3个角度中的最大值为0.000 8°，小于0.001°，实现了预期目标。经测量，空间站舱体水平旋转装备在长度方向上的最大变形量为0.074 mm，不会影响其使用寿命。

4 结 论

本文针对空间站舱体水平旋转装备提出了六点调平算法及同步控制方法，有效地避免了该装备负载30 t后在长度方向上产生变形的问题，提高了其上平面的水平度，延长了其使用寿命，同时确保了空间站舱体放置在水平旋转装备上后的质心稳定及结构不发生变形，为后续总装过程提供了优质的保障。