基于接触应力优化的摆线轮修形设计
赵致勃,顾大强,李立新,张 靖
(1.浙江大学机械工程学院,浙江杭州 310000;2.浙江环动机器人关节科技有限公司,浙江台州 318000)
RV(rotary vector,旋转矢量)减速器是工业机器人中的关键零部件,具有结构紧凑、传动比大、振动小以及传动效率高的优点[1-2]。摆线轮齿廓修形技术是RV减速器加工制造中的核心技术[3-4],通过对摆线轮进行合理的修形,可以改善RV减速器的传动性能[5]。我国的RV减速器以进口为主,国产减速器与世界一流减速器相比有一定的差距。因此,对摆线轮修形技术展开深入研究具有重要意义[6]。
传统的摆线轮修形方式有移距修形、等距修形和转角修形等,在实际生产中多采用组合修形方式。陆龙生等[7]提出一种以摆线轮齿面啮合力为优化目标的组合修形方法。关天民等[8-11]对摆线轮的组合修形方式进行了进一步的研究,并提出了可以保证啮合力的“反弓”齿廓。张飞翔[12]提出了基于多项式的摆线轮分段修形方法,该方法将摆线轮齿廓分为齿根段、工作段和齿顶段:对于齿根段和齿顶段,为保证一定的径向间隙,将这2段的修形量设为多项式函数;对于工作段,为保证共轭啮合,该段采用标准摆线齿廓。丁国龙等[13]提出了一种基于接触应力均化的摆线轮修形方法,即以转角修形齿廓为目标齿廓,采用等距和移距组合修形逼近方法确定相应的修形量。邓纪辰[14]利用有限元分析软件ANSYS建立了摆线轮与针齿的接触模型,分析了摆线轮齿廓接触应力的分布情况。
上述方法在一定程度上可实现摆线轮齿廓接触应力的均化。为进一步降低摆线轮齿廓的接触应力,以改善其传动性能,笔者基于反弓齿廓提出了一种两段修形方法,即根据要求在摆线轮齿廓的不同位置处采用不同的修形量,使得齿廓接触应力的分布更加合理。同时,分别通过理论计算和有限元仿真分析来验证两段修形方法的可行性。
1 摆线轮齿面受力分析
1.1 摆线轮的齿廓方程
标准摆线轮经等距、移距组合修形后,其齿廓方程可表示为[15]:
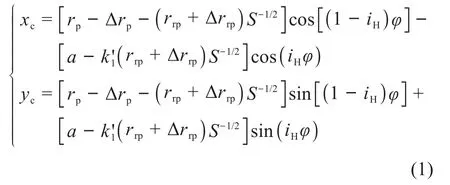
其中:
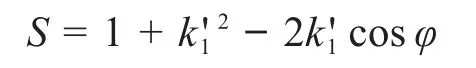
式中:rp为针齿中心圆半径;rrp为针齿半径;Δrp为移距修形量;Δrrp为等距修形量;iH为传动比,iH=zp/zc,其中zp为针齿数,zc为摆线轮齿数;φ为针齿中心相对于转臂的转角(下文简称针齿转角);a为偏心距;k1'为移距修形时的短幅系数,。
1.2 组合修形产生的几何回转角
摆线轮组合修形时产生的几何回转角β可表示为[8]:

结合摆线轮与针齿的径向间隙Δj=Δrp+Δrrp,可得临界等距/移距修形量Δrrp0、Δrp0,分别为:
临界等距/移距修形量Δrrp0、Δrp0是几何回转角β在φ=φ0=arccosk1'处取得极大值和极小值的分界点。当Δrrp<Δrrp0时,β在φ=φ0处取得极小值;当Δrrp>Δrrp0时,β在φ=φ0处取得极大值,且在φ0前后各有1个极小值(设这2处极小值位置分别为φa、φb)。通过计算可得:
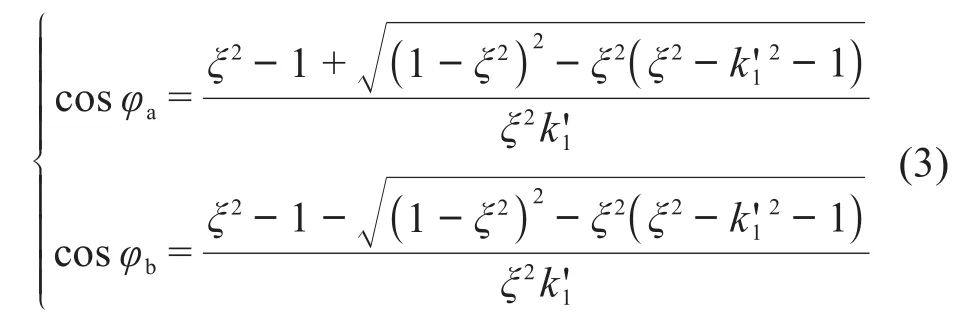
其中:

利用式(3)即可求得φa、φb。
1.3 组合修形后的啮合区间
在构建摆线轮齿面受力分析模型时,假设变形仅发生在摆线轮与针齿啮合的位置处,其余位置不发生变形[15]。
组合修形后的摆线轮在空载时,其各轮齿与针齿之间存在宽度不同的初始啮合间隙Δ()φj[8]:
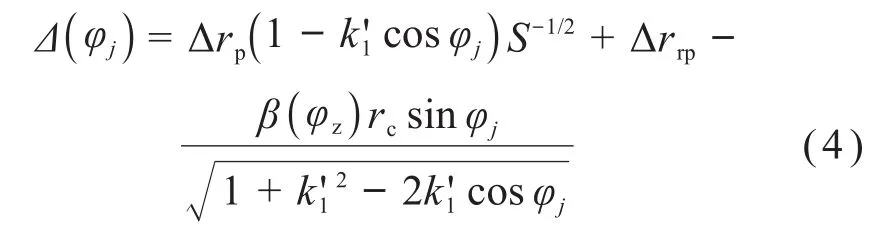
式中:rc为摆线轮节圆半径,rc=azc;φz为最先啮合点处的针齿转角;φj为第j颗摆线轮轮齿对应的针齿转角。
摆线轮与针齿最先啮合点处的总变形量δmax为:

其中:

式中:wmax为摆线轮与针齿的接触变形量;fmax为针齿的弯曲变形量,对于卧枕式针齿,其弯曲变形量可以忽略不计[15];μ为摆线轮与针齿材料的泊松比;E为摆线轮与针齿材料的弹性模量;b为摆线轮厚度;Fmax为最大啮合力;ρz为最先啮合点处的齿廓曲率半径;Fmax和ρz均参照文献[15]中的方法计算。
摆线轮与针齿的任意啮合点处的总变形量δj为:
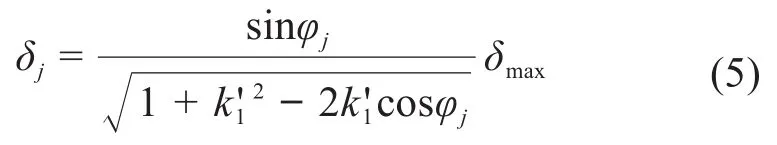
根据摆线轮与针齿的初始啮合间隙和啮合点处的总变形量,即可确定摆线轮的啮合区间。
1.4 啮合力与接触应力计算
组合修形后摆线轮的第j颗啮合轮齿的啮合力Fj可表示为[15]:

摆线轮第j颗啮合轮齿的接触应力σHj按赫兹公式进行计算[16]:

式中:ρj为第j个啮合点处的齿廓曲率半径;分子中取正号表示外接触,取负号表示内接触。
结合式(6)和式(7),可得组合修形下摆线轮齿廓的接触应力随修形量的变化情况。
2 摆线轮的两段修形方法
已知齿轮的承载能力与接触应力关系密切[17]。为了进一步降低摆线轮反弓齿廓的最大接触应力,以提高其承载能力,提出了一种两段修形方法。
对摆线轮反弓齿廓的啮合力与接触应力(见图1)进行分析可知,虽然反弓齿廓可以产生较好的齿面受力状态[8],保证最先啮合点有2个(φa和φb),且这2个点处的啮合力均最大,但从图1(b)所示的接触应力看,摆线轮齿廓已不再保留反弓形状,最大接触应力仅在φb附近取得。通过分析赫兹公式可以得出,2个最先啮合点的接触应力不同是因为这2个啮合位置处的齿廓曲率半径不同,与针齿的接触状态一个为外接触,另一个为内接触。故可以通过两段修形的方式来使摆线轮接触应力最大的位置在空载啮合时具有一定的初始间隙,即改变该啮合点处的齿廓曲率半径。综上,两段修形方法是在反弓齿廓的基础上,先将摆线轮的齿廓分为2段,再对不同工作段的齿廓采用不同的组合修形量,最终达到降低齿廓接触应力的目的。

图1 摆线轮反弓齿廓啮合力与接触应力分布示意Fig.1 Schematic diagram of meshing force and contact stress distribution of cycloidal gear inverse archshaped tooth profile
2.1 齿廓分段区间确定
摆线轮反弓齿廓啮合力最大的位置是在φa和φb附近,而接触应力最大的位置在φb附近。因此,以φ0为分界点,将摆线轮的齿廓分为两部分:第1段,0°~φ0;第2段,φ0~180°。
2.2 不同分段区间组合修形量确定
第1段齿廓的接触应力较小,无需改善,故该段仍采用原反弓齿廓的组合修形量。
第2段齿廓出现最大接触应力,需要进行改善,采用修形量变化的组合修形方法,即将等距修形量和移距修形量定义为关于针齿转角的多项式函数。为了保证啮合平稳,必须使2个工作段的连接处光滑[18],故将修形量设为关于针齿转角的二次多项式函数,其中等距修形量曲线如图2所示。结合摆线轮与针齿的径向间隙,可确定移距修形量曲线。

图2 基于两段修形的摆线轮齿廓的等距修形量曲线Fig.2 Isometric modification quantity curve of cycloidal gear tooth profile based on two-stage modification
2.3 两段修形产生的几何回转角
由上文分析可知,修形产生的几何回转角的大小由最先啮合点确定,故需要找出两段修形后摆线轮的最先啮合点。
采用两段修形方法后,摆线轮第2段齿廓的初始啮合间隙比反弓齿廓略大,故最先啮合点仅有1个,在φa位置处,产生的几何回转角与原反弓齿廓的相等,可根据式(2)确定。
修形对摆线轮传动精度的影响是由几何回转角决定的。采用两段修形后新齿廓的几何回转角与反弓齿廓相同,故新齿廓在能够保证传动精度相同的基础上,具有更好的承载能力。
3 实例分析
3.1 修形量确定
以RV-40E减速器为例[12],通过计算得到基于两段修形的摆线轮的组合修形量。RV-40E减速器的基本参数如表1所示。

表1 RV-40E减速器的基本参数Table 1 Basic parameters of RV-40E reducer
基于两段修形方法原理和表1参数,计算得到的RV-40E减速器摆线轮的组合修形量如下:
对于第1段齿廓(0°~36.122°),仍采用原反弓齿廓的组合修形量。借助MATLAB软件进行一维寻优,计算得到等距修形量Δrrp=0.6 mm,移距修形量Δrp=-0.375 mm。
对于第2段齿廓 (36.122°~180°),为保证其与第1段齿廓的连接光滑、平稳,在φ0=36.122°处的组合修形量仍取Δrrp=0.6 mm、Δrp=-0.375 mm。由上文分析可知,当径向间隙Δj固定时,等距修形量Δrrp越大,摆线轮整体的初始啮合间隙越大。为了改善齿廓的最大接触应力,应使第2段齿廓的初始啮合间隙比反弓齿廓的大。经过多次计算,最终确定φ=180°处的组合修形量为Δrrp=0.825 mm、Δrp=-0.6 mm时效果较为理想。
根据φ0=36.122°和φ=180°处的组合修形量,可以确定第2段齿廓的等距修形量:

结合径向间隙和式(8)即可确定相应的移距修形量。将摆线轮的2段齿廓的组合修形量代入式(1)即可得到新齿廓的方程。
3.2 新齿廓与反弓齿廓对比
利用MATLAB软件编写摆线轮受力分析程序,并将新齿廓与反弓齿廓的啮合力和接触应力进行对比,结果如图3所示。由图3可知,虽然新齿廓的最大啮合力比反弓齿廓大,啮合区间比反弓齿廓小,但最大接触应力比反弓齿廓低。新齿廓的最大接触应力为1 631.6 MPa,比反弓齿廓的最大接触应力1 780.1 MPa降低了8.34%。

图3 2种齿廓的啮合力和接触应力对比Fig.3 Comparison of meshing force and contact stress between two tooth profiles
4 摆线轮齿廓接触应力有限元分析
利用三维软件Creo建立摆线轮传动的参数化模型,并将其导入ANSYS Workbench软件,以对摆线轮齿廓的接触应力进行静力学分析。
4.1 前处理
结合RV-40E减速器的基本参数,考虑摆线轮的实际传动过程以及计算机资源的限制,以及摆线轮与针齿的接触分析可归类为平面应变问题,故接触模型采用平面模型。由于RV-40E减速器采用卧枕式针齿结构,则针齿与针齿槽之间的接触变形忽略不计,故将针齿壳与针齿作为整体考虑。在完成摆线轮传动的参数化模型的构建后,先设置材料属性:摆线轮与针齿的材料取GCr15SiMn,其密度为7 820 kg/m3,弹性模量为2.06×105MPa,泊松比为0.3,许用接触应力为3 800 MPa。然后,进行网格划分,网格单元类型为PLANE183,整体网格尺寸为1 mm,将摆线轮与针齿表面的网格细化并调整相关性,使网格纵横比尽可能接近1,以保证网格划分质量,从而保证有限元仿真结果的收敛性和准确性。
完成网格划分后,定义摆线轮与针齿的接触关系。考虑到摆线轮与针齿的接触变形对接触刚度的影响,以及摆线轮与针齿的材料相同,将两者均定义为柔性体;根据目标-接触凹凸面的选取规则,定义摆线轮齿面为接触面,针齿表面为目标面;接触设置为摩擦接触,摩擦系数为0.1;接触界面处理选择用户指定偏移数值,逐渐施加载荷,有利于提高收敛性;接触算法选择较容易收敛的增广拉格朗日法。考虑到摆线轮与针齿接触时,其齿面法向刚度会因接触区间的变化而不断变化,属状态非线性问题,故设置每次平衡迭代后自动更新接触刚度;时间步长控制设置为预测冲击,可自动预测接触行为突变的最小时间增量并分割子步。
最后,定义载荷和约束。将针齿壳外侧圆柱面定义为圆柱面约束,径向固定,释放切向自由度;同时,在针齿壳外侧圆柱面加载206 N·m工作扭矩(RV-40E减速器有2个摆线轮,故负载减半);对摆线轮的2个曲柄轴孔施加固定约束。
综上,构建的摆线轮与针齿接触的有限元模型如图4所示。

图4 摆线轮与针齿接触的有限元模型Fig.4 Finite element model of contact between cycloidal gear and needle tooth
4.2 求解及结果分析
为了能够反映摆线轮齿廓接触应力的真实分布情况,采用不同尺寸的网格对啮合位置处的齿面进行划分并分别进行求解。
表2所示为2种齿廓在不同网格尺寸下的最大接触应力。由表2可以看出,在不同网格尺寸下,新齿廓的最大接触应力均比反弓齿廓的小;最大接触应力在网格尺寸达到0.010 mm时已逐渐开始收敛,继续减小网格尺寸后结果差异并不明显,但计算量急剧增加。鉴于网格尺寸越小,仿真结果越能真实反映摆线轮齿面的受力情况,本文选择0.005 mm的网格尺寸。

表2 不同网格尺寸下2种齿廓的最大接触应力Table 2 Maximum contact stress of two tooth profiles under different mesh sizes
图5(a)所示为网格尺寸取0.005 mm时摆线轮新齿廓最先啮合点处的接触应力分布云图;图5(b)所示为网格尺寸取0.005 mm时新齿廓与反弓齿廓的接触应力对比。由图可知,新齿廓同时啮合的齿数为7对,反弓齿廓为8对;新齿廓的接触应力分布较反弓齿廓均匀,其最大接触应力为1 990.3 MPa,比反弓齿廓的最大接触应力2 081.6 MPa降低了4.39%。由此说明,啮合齿数越多并不能代表摆线轮齿廓的接触应力越低,且结果验证了两段修形方法的可行性。

图5 摆线轮齿廓接触应力的有限元仿真结果Fig.5 Finite element simulation results of contact stress of cycloidal gear tooth profile
图6所示为2种齿廓接触应力有限元仿真结果与理论计算结果的对比。由图6可以看出,基于2种方法得到的摆线轮的啮合区间基本相同,反弓齿廓最大接触应力的仿真结果为2 081.6 MPa,与计算结果1 780.1 MPa相差14.48%;新齿廓最大接触应力的仿真结果为1 990.3 MPa,与计算结果1 636.1 MPa相差17.79%。产生误差的原因可能有以下几点:1)理论计算时假设摆线轮整体为刚性,仿真分析时则假设整体为柔性;2)仿真分析时考虑了摆线轮上通孔的影响,理论计算时则没有考虑;3)其他可能产生误差的因素。其中,刚柔假设的不同对结果的影响最大。综上,仿真结果与计算结果的相对误差为14%~18%,在允许范围内。考虑到理论计算模型和有限元模型均进行了简化,由此可验证两段修形方法的可行性。

图6 2种齿廓接触应力的有限元仿真结果与理论计算结果对比Fig.6 Comparison between finite element simulation results and theoretical calculation results of contact stress of two tooth profiles
5 结论
通过建立摆线轮的受力分析模型,探究了组合修形量与其啮合力、啮合区间的关系,以及反弓齿廓的形成条件;在反弓齿廓的基础上,提出了一种可以降低最大接触应力的两段修形方法。最后,以RV-40E减速器为例,分析了两段修形后摆线轮的受力情况,并对新齿廓与反弓齿廓进行了比较。有限元仿真结果表明,两段修形方法可以降低齿廓的接触应力,可为摆线轮的加工制造提供一定的参考。
研究发现,摆线轮修形后的啮合区间越大并不意味着其接触应力越小及承载能力越强。以RV-40E减速器为例,两段修形后新齿廓的啮合齿数为7对,反弓齿廓的啮合齿数为8对,但新齿廓的最大接触应力却明显降低。不过本文在仿真分析时考虑到计算资源和时间的限制,采用的是平面模型,建议进一步研究时采用三维模型,并考虑曲柄轴、轴承以及第一级渐开线行星齿轮的影响。

