行成于思 备战中考
——以“相似三角形”的复习课为例
⦿江苏省如皋市丁堰镇初级中学 黄晓兰
1 引言
当前,初中九年级数学的备考教学已经成为一种固定化的模式:将初中6册课本再次“敲打”一遍,从课本的字里行间去梳理重要知识点,对中考的考试大纲和近几年各地的中考数学试题进行揣摩、研析,洞察中考试题的命题特点、规律和走势.教师通过海选各地的模拟题,组织适应中考的专题,然后是考、备、讲、批、纠……好像这种循规蹈矩的做法就是对毕业生的负责.然而,题海战术让师生身心疲惫,在教育主管部门一再强调“减负”的背景下,又有何良策让师生解放出来,同时在中考的战场上扬鞭策马呢?笔者在教学实践中一直在不断地反思.
2 在教学实践中多揣摩、研析教法,行成于思
笔者多次任教九年级的数学课,在备考的同时也在积极找寻一种务实的方法,期望能实现训练减少、效益提高,以运用于毕业班数学教学实践.通过多年的揣摩、研析,笔者领悟到毕业班数学教学的灵魂在于“学法指导”.
随着初中毕业班备考复习的深化,学生对初中数学知识进行了再次整合,学习成绩发生质的飞跃,这个时期学生已经掌握初中数学的全部基础知识,通过复习可以帮助他们建立知识网络.如在“相似三角形”的复习时,帮助学生建立如图1的知识结构.
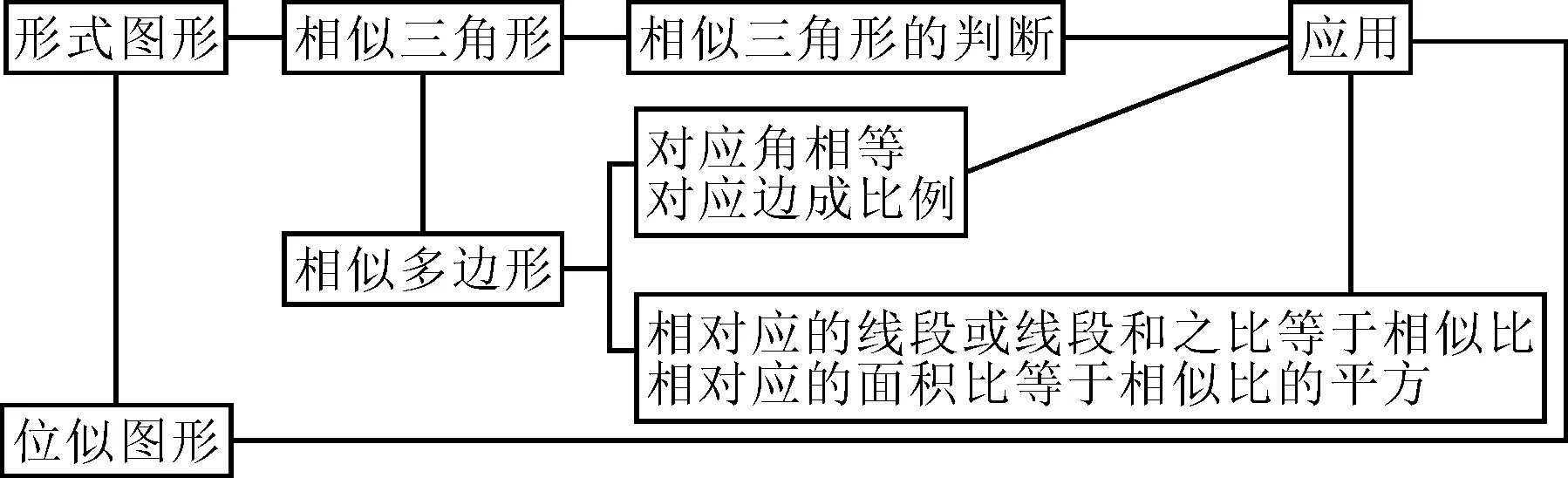
图1
3 在教学过程中引导学生做到对知识的懂、通、透、活
数学是枯燥的理论与原理在实际情境中的抽象应用相结合的学科,对知识的懂、通、透、活,换一句话说就是对数学要做到明白原理、理解规律、渗透联想、迁移运用[1].这些环节其实质就是一种学习技能与方法,简称为“学法”.
3.1 明白数学原理是根本,要“懂”复习专题的知识体系
经历了两年多的初中学习生涯,学生对数学的“双基”都能“懂”,对数学考查知识的“标高”、应用、专题知识结构也能略知一二,只要让学生对这些内容做到每节课、备考的每一天都能回放即能达到目的[2].构建数学知识体系、内化为应用是“懂”的前提,并非需要三天两头的测试.教师不断地选题、学生不停地做题,教师不舍昼夜地批改、学生加班加点地纠错,师生都累得气喘吁吁、疲惫不堪.同时学生对大量的试题不能细嚼慢咽、消化吸收,造成抵触情绪,学习只能停滞不前,随之视数学为累赘,久而久之就会产生厌恶感.因此,帮助学生构建必要的知识体系,需要教师细心呵护,“授之以渔”.在“相似三角形”的专题复习时,笔者认为首先应让学生在相似三角形的知识回顾中重新整合相关知识点,让不同的知识板块如多边形和直角坐标系等之间相互渗透,主动构建相似三角形的知识网络,然后让学生去综合运用,提升实战能力.课堂教学知识回顾可以借助中考试题作为典型例题来整合:
典例(2019年扬州市中考试题)如图2,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,其中AB⊥BC,AE⊥ED,CD与BE,AE分别交于点P,M.对于下列结论:

图2
①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是______.(填序号)
分析:①是确定△BAE∽△CAD时,可以通过Rt△ABC和Rt△ADE三边关系(勾股定理),得出△BAE与△CAD对应边成比例进行判断,复习判定定理;

③需要转化,2CB2=AC2,再证明△PCA∽△ACM.解决问题时用到了A,D,E,P四点共圆.
设计意图:让学生从简单到繁杂,从直接到转化,应用相似三角形的判定定理来解决问题.不但构建了相应的知识结构,而且也帮助学生认清了知识的“标高”和中考的方向.
3.2 理解数学规律是过程,要对知识进行通识
所谓的“通”是对知识的通识,是一种变通.初中毕业班学生对数学的“通”可以从突破考试大纲做起.教师需要认真解读考试大纲中的内容,引导学生从中悟出数学知识的本质,在数学知识的回忆中建立知识体系,不需要“题海战术”.从专题的角度来看,数学知识和考点并非很多,但学生做题占用了超过三分之一的时间,所得到的结果常常事与愿违.从近几年各地市的中考数学试卷来看,题目的总体难度并非很大,而学生交出的答卷总是不尽人意,这是“题海战术”使中考备考迷失了方向.因此,在“相似三角形”专题复习中,笔者用了六个知识点作为考向:
①线段比例与黄金分割;
②图形的相似性与相似三角形;
③重要的相似图形的证明方法;
④函数中的三角形相似的应用;
⑤圆与相似三角形的关系(切割线定理);
⑥动点产生的相似问题(极小值与对称性)的应用.
将这六个知识点按1∶2的例题与变式练习配比去强化,不但可以整合知识结构,同时也可利用相似三角形解决具体情境的建模.
3.3 拓展数学知识,找到问题情境中知识的联想点
什么是“透”?数学中的“透”是透过问题情境现象抓住数学建模的本质.当下许多教师以“练习、纠错,再练习、纠错……”作为制胜的法宝,认为“学生不可能在一碗水中学会游泳,只能跳入大海才有学会游泳的可能”,大量训练题铺天盖地而来,让学生在题海中感悟数学,应用数学,达成“透”的愿景.在疲于应付的情况下,这种做法适得其反,淡化了合作、探究等学习方式.
正确之举是采用知识的高起点而落差小的数学训练,适当拓宽知识面,让学生在复习备考中感受满满的喜悦.例如,在典例中,教师只是具体地引导,而不是将答案一股脑地呈现给学生.教师可以适度提示,如典例③,A,D,E,P四点共圆是怎样联想的?△PAC为什么与△AMC相似?(让学生发现2CB2=AC2=CP·CM,这与切割线定理形式是相同的.)
3.4. 传授数学的知识之“渔”,学会知识的迁移运用
“活”是学习的灵魂,是现在中考立意的境界.没有教师的“渔”,只有学生的“鱼”,盲目蛮干式的题海战术,学生不仅消耗大量的时间,为了完成任务倍数巨大的压力,当然不会活起来.要使学生备考复习学有所成,就必须做到“精准”,教师精讲、学生精练.在“精准”中让学生体验“渔”的活用.
例如,在“相似三角形”专题中创设的问题情境让学生发掘出图形中的平行线型、交叉线型和旋转型的情形.前面所列举的典例就可以看作是等腰直角三角形在点A的旋转.
4 结束语
在中考备考的课堂教学中,教师对学生的学法指导尤其重要.毋容置疑,教师只有在教学实践中多揣摩、研析教法,行成于思,才能在教学过程中正确引导学生做到对知识的懂、通、透、活.如此,学生一定会把握自我学习的主动权,一定能从有效学习中收获知识与方法,快速提升数学学科素养[3].

