“双减”背景下作业分层设计策略及实践

⦿安徽省安庆市望江县长岭初级中学 刘 发

1 引言

去年，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(简称“双减”).“双减”强调“提高作业设计质量”，“鼓励布置分层、弹性和个性化作业”.这样就改变了传统作业“一刀切”的模式，提高了学生学习的内在动力.“弹性和个性化作业”是为了符合学生的个人要求，让学生的个性自由飞扬，因此在设计作业时，应该因材施教，因人而异，使各个层次的学生都能够自由地选择自己需要的作业，这样才可能真正减轻学生过重的作业负担.

2 学生分层

设计分层作业之前，教师可在班主任的协助下主要依据学习成绩，同时还要充分考虑学生的兴趣、爱好、能力等方面的差异性，将学生分为A、B、C三个层次.对A层次和少数B层次的学生，通过谈心，建立自信，维护他们的自尊，从而调动他们的积极性.A层次：学习中不肯动脑筋，习惯不好，基础题难以完成.B 层次：基础不牢固，综合解决问题的能力较弱，成绩不稳定.C层次：基础扎实，兴趣浓厚，思维能力较强，综合解决问题的能力较强，成绩较为突出.学生分层是动态的，通过一个月的学习，对在课堂提问、当堂练习和考试中进步明显的学生，则相应调整到高一层次.反之，则下降一个层次.

3 分层作业

分层作业就是指老师为帮助学生掌握数学知识和提升核心素养，鼓励学生各方面能力得到逐步提高，按照不同学生的学习能力、个性特征和不同难易程度的课程内容，提出不同的要求，并给出不同的评价标准而设计的作业.分层作业不仅要体现人性化、个性化，更要体现发展化[1].

在硬性分层和学生自愿的基础上，鼓励学生完成高层次的作业，但要注意防止学生好面子盲目选择高层次的作业.对完成上一个层次作业和解法简便的学生，除全对得到满分外，还可“加分”予以鼓励.

4 分层作业设计的策略

4.1 根据教学目标体现分层

教学目标要严格按照课程标准制定，它既是分层作业设计的出发点和落脚点，也是分层作业设计的核心和灵魂.要提高作业的质量，需要面向全体，将每一知识点的作业目标加以细分，使每道题目对应一个具体的目标.

案例1根据沪科版七年级下册“10.3平行线的性质”教学目标设计如下三级课后作业:

A层次:我会做(★).

(1)如图1，已知直线a∥b，∠1=40°，则∠2的度数是( ).

A.40° B.60° C.80° D.140°

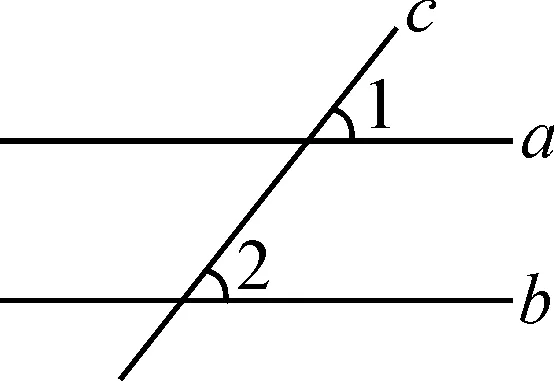
图1

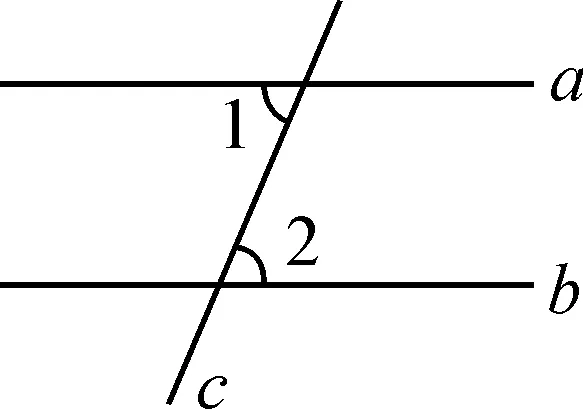
图2

图3

(2)如图2，已知直线a，b被直线c所截，且a∥b，若∠1=75°，则∠2的度数是.

(3)如图3，已知AB∥EF，∠CDB=80°，求∠ADF和∠F的度数.

B层次：我能做(★★).

(4)如图4，将直尺与含60°角的三角尺叠放在一起，60°角的顶点落在直尺的一边上，其两边与直尺相交，若∠2=80°，则∠1的度数是( ).

A.100° B.80° C.60° D.40°

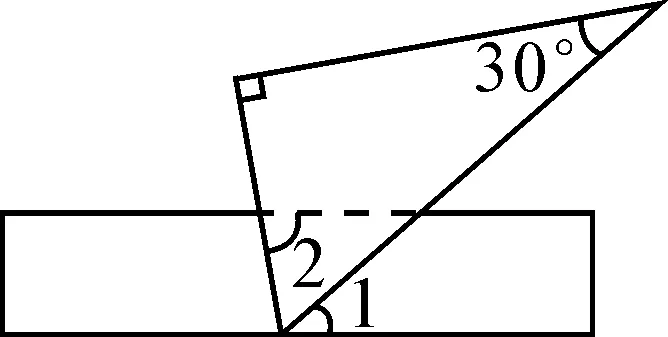
图4

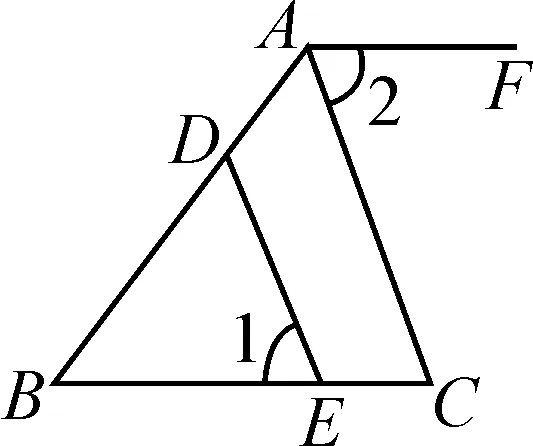
图5

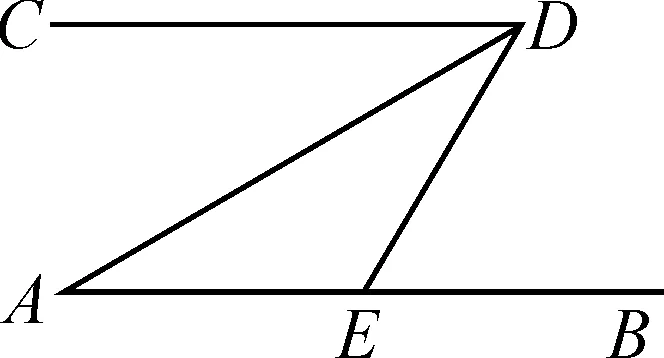
图6

(5)如图5，点D,E分别在AB,BC上，DE∥AC，AF∥BC，∠1=72°，则∠2=.

(6)如图6，AB∥CD，∠A=35°，DA平分∠CDE，求∠DEB的度数.

C层次：我要做(★★★).

(7)如图7，一个四边形纸片ABCD，∠C=90°，将纸片按如图所示折叠，使点A落在BC边上的点A′，BE是折痕.若A′E∥CD，∠D=118°，则∠ABE的度数是( ).

A.62° B.60° C.31° D.30°

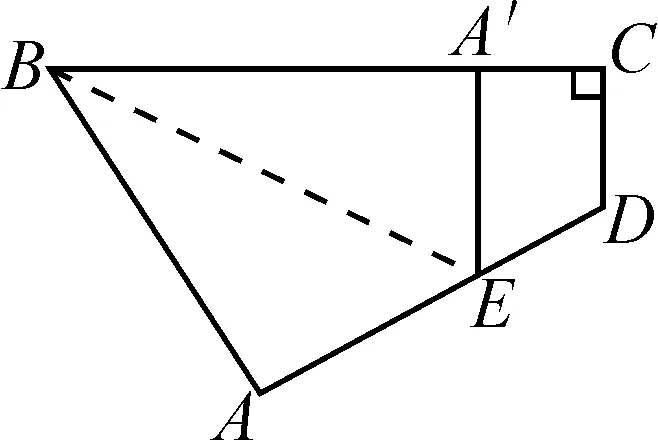
图7

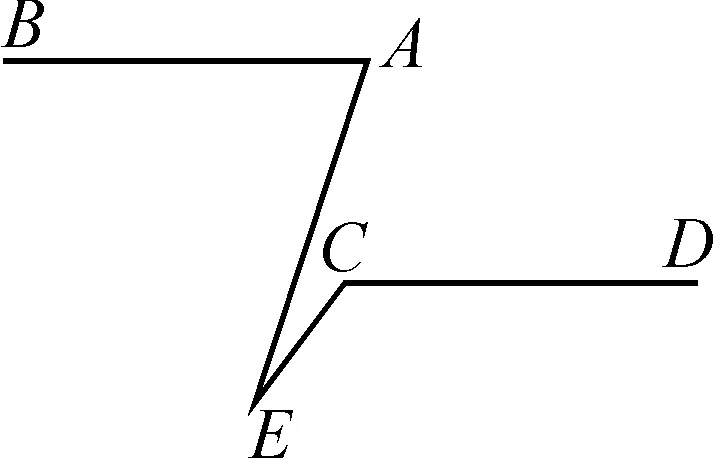
图8

图9

(8)如图8，已知AB∥CD，∠E=15°，则∠A+∠C=.

(9)如图9，一副直角三角板(∠ACB=45°，∠FED=60°，∠A=∠D=90°)的BC，EF边分别与直线a，b重合，且a∥b，将△ABC，△DEF分别绕点C，F以4度每秒和1度每秒的速度同时逆时针旋转，△ABC转动一周时两块三角板同时停止.问需要旋转多长时间时，AC，DF所在直线互相垂直？

点评：A层次学生，能通过“我会做”巩固基础知识，第(1)(2)题直接运用平行线的性质求解，在第(3)题中直接运用对顶角和平行线的性质求解.该层次的作业难度系数在0.9左右，考查的知识点为1个.B层次学生，能够利用“我会做”进一步巩固并灵活运用角平分线的定义和平行线的性质等知识.该层次的作业属于“思维拓展性作业”，难度系数在0.6左右，考查的知识点为2个或3个.C层次学生通过“我要做”挑战自我，添加辅助线创造性地运用平行线的性质与判定，综合考查分类讨论思想、方程思想和数形结合思想解决问题的能力.该层次的作业属于“探究开放性作业”，难度系数在0.2左右，考查的知识点为3个或3个以上.

4.2 在一题多解中体现分层

同一道题目，从不同的角度去思考，可能得到不同的解法.一题多解是培养学生数学思维能力的一条重要途径，能够满足学生个性化的发展，较好地面向全体.对典型题目，向各层次的学生提出解法数量要求，达到要求的获满分，超过要求的和解法简便的均获得“加分”.

案例2如图10，在△ABC中，∠BAC=90°，AB=AC，D为AC中点，AE⊥BD于点E，延长AE交BC于点F.

求证：∠ADB=∠CDF.

图10

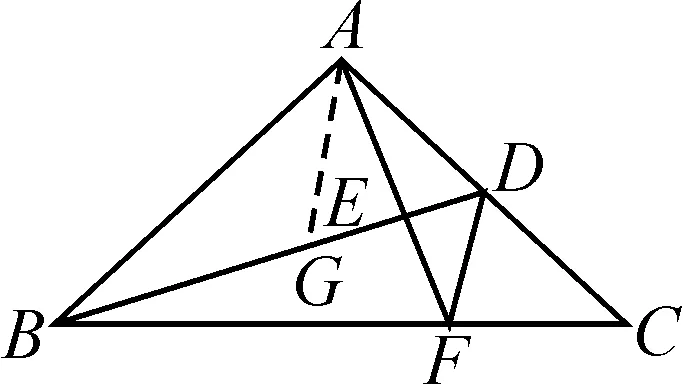
图11

对本例，学生出现最多的三种思考方法是：(1)如图11，过点A作AG平分∠BAC，交BD于点G，证明△AGD≌△CFD即可.(2)如图12，过点A作AG平分∠BAC交BD于点G，过点D作DH⊥CF于点H，易得∠ADB=∠BAE= ∠BAG+ ∠GAE=45° +∠GAE，∠CDF= ∠CDH+ ∠FDH=45° + ∠FDH，再证∠GAE= ∠FDH即可.(3)如图13，过点C作CI∥AB交AF延长线于点I，易得△ABD≌ △CAI，则 ∠ADB= ∠AIC，AD=CI.再证△FCD≌△FCI得∠FDC=∠FIC，从而得出结论.

图12

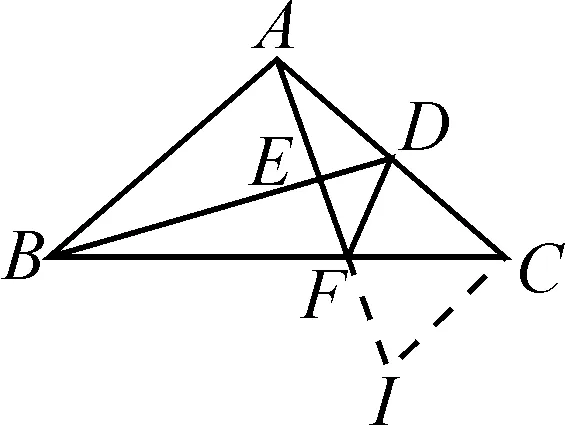
图13

点评：本设计满足了学生个体差异的需要，有利于全体学生的发展，有利于学生超越自我，挑战极限，让各层次的学生都能收获别样的精彩!

4.3 在一题多问中体现分层

一题多问就是将一道解答题分成多个小问题，以层层递进的方式呈现，前面的小题是为后面小题做铺垫.当“后进生”和“中等生”面对一个问题不知所措时，教师可把它设置成几个与此相关的小题，降低难度.这样有利于增加他们的信心，促使他们进一步思考，还可让学生在此基础上自己提出问题.爱因斯坦曾说过，提出一个问题往往比解决一个问题更重要！提出好的问题，有时能够使题目更加灵动，更加能激发学生思考.根据所提问题的质量，对不同层次的学生给出不同的“满分”和“加分”标准.

图14

案例3如图14，在四边形ABCD中，AB⊥BC，∠BAD+∠BCD=180°，AE，CF分别平分∠BAD，∠BCD，分别交BC，AD于点E，F(点E与C不重合).在线段CF上取点P，Q(点P在CQ之间)，使CP=2FQ.当点G从点A匀速运动到点E时，点H恰好从点P匀速运动到点Q.设HQ=x，AG=y，6x+5y=60，当H为CF中点时，y=4.8.

(1)求证：AE∥CF.(A层次)

(2)求AE，PQ，CP的长.(B层次)

(3)若AB=6.

①当AG=AF时，求CE和CH的长；

②连接GH，当GH所在直线经过四边形ABCD的直角顶点时，求HQ的长.(C层次)

点评：本例属于四边形的动态探究类问题，综合性强，涉及的知识较多，考查了抽象意识、推理能力、运算能力等核心素养.对A层次的学生只要完成第(1)问即可得满分；B层次的学生需完成(1)(2)问才能得满分；C层次的学生需完成整个题目才能得满分.超过要求的，则加分！有创新的解法和有价值的提问均应加分！如有的C层次的“学优生”提出：连接GH，当GH所在直线经过四边形ABCD的一个顶点时，HQ的长是多少？开放程度加大了，难度也加大了，分类的情况更多.这样的提问，值得加分！

4.4 通过动手操作体现分层

通过动手操作能够让不同层次的学生在形象思维、发散性思维和创新性思维上得到不同程度的提高.

案例4在上完沪科版八年级下册“18.1勾股定理”第一课时后,我布置了课后作业：请同学们查阅资料，动手操作验证勾股定理，画出其拼图，写出拼图的创始人和验证方法.

拼图的创始人主要有邹元治、赵爽、茄菲尔德、毕达哥拉斯、梅文鼎、项明达、欧几里得、辛卜松、陈杰、杨作玫、李锐等等.学生对这个问题的验证方法很多，如利用相似三角形性质证明等.

点评：学生们兴趣盎然，都能积极动手拼图，至少找到了一种验证方法，有的找到了多种验证方法，还有学生独创了一种或多种验证方法！通过拼图验证活动，学生们体会到数学的和谐美、简洁美！同时他们受到良好的数学文化熏陶， 特别是了解了我国古代在勾股定理研究和运用方面的成就，激发了他们的爱国热情！

4.5 通过数学日记体现分层

数学日记属于开放性的自主建构型作业，与语文日记有些类似，但也有不同，它主要是以日记的形式，记录课内和课外对数学的想法、体会以及疑惑等.数学日记根据学生的实际情况而定，形式多样，其内容主要有预习型和反思型两种，其中有听课后的反思、解题过程与方法的反思、纠错的反思等等.根据写作情况，制定“满分”和“加分”的标准，如“纠错反思”有的学生不仅有“正解”，而且列举了类似题目进行举一反三就应获得“加分”[2].

点评：数学日记重视了学生的个人差异性，内容充满了个性化、人情味，有效改变了传统数学作业的“一刀切”的现象，使众多的学生不再将数学作业当成负担，从而让不同层次的学生都有所发展!

5 小结

实践证明，按照以上方案设计的分层作业，学生完成作业的兴趣和质量都要远高于传统的“一刀切”的作业.同时，通过学生在每一次大考中的成绩分析，可以发现分层作业设计对学生的成绩产生了积极正向的影响，切实减轻了学生过重的作业负担.但以上策略也不是减负的完美理想方法，因此需要我们不断地寻求和探索，才能丰富自己的作业设计经验和实践，才能更好地落实“双减”政策.