STEAM教育理念下的初中数学教学设计——以“不等关系”为例

⦿阜阳师范大学 吴缘缘 刘芳瑶 储亚伟

1 STEAM教育的背景

20世纪50年代，苏联卫星上天，美国举国震惊，开始反思自身教育的不足并意识到科技发展的重要性，由此美国开始加强K12关于科学、技术、工程、艺术以及数学的教育.1986年，美国国家科学基金会(NSF)在《本科的科学、数学和工程教育》报告[1]中提出“科学、数学、工程和技术教育集成”的纲领性建议，这也被视为STEAM教育的开端.此后30年，美国逐渐将STEAM教育理念提升到国家战略发展的层面，先后出台多条法规政策，推动STEAM教育的全国性、全阶段发展.

随着美国对STEAM教育的重视，欧亚各国开始纷纷效仿，开展了许多对STEAM教育的研究，尤其是澳大利亚政府对于STEAM教育的发展给予了高度重视和支持[2].可以看出，STEAM 教育理念自提出以来，就展现出了昂扬的生命力和迅猛的发展势头，其强大的学科包容性和知识整合性顺应了知识经济背景下各国发展对人才的新要求.中国对于STEAM教育的开展较其他国家更晚一步.2015年9月教育部《关于“十三五”期间全面深入推进教育信息化工作的指导意见(征求意见稿)》首次明确提出STEAM教育[3].2017年，以“新战略、新课改、新高考”为主题的首届“中国STEAM教育发展大会”在成都电子科技大学举办.迄今为止，中国已成功召开了五届STEAM教育大会，结合中国新时代的教育背景与国际趋势，期望推动形成中国STEAM教育的新格局.

在国内新高考改革的背景下，文理分科已成为过去式，跨学科整合教学逐渐成为刚需.中小学“双减”政策的提出，要求在减少作业与校外培训的同时更要提高学校教育质量.各地方政府和学校纷纷开展以STEAM教育理念为指导的课程改革与教学实验，并取得了一定的实践成果.但要探索出适合中国普适化的STEAM教育模式还有漫漫长路.

2 理论基础

STEAM教育是指由科学(Science)、技术(Technology)、工程(Engineering)、艺术(Art)、数学(Mathematics)等学科共同构成的跨学科课程.当今学界对于STEAM教育的认识说法不一，文章中采用的STEAM教育定义为在真实问题情境中以跨学科整合的方式培养创新人才的一种教育类型，是基于项目或问题的方式培养学生STEAM素养的教育[4].

STEAM教育的本质是综合课程的教育，可以弥补传统教学模式知识联系较少的缺点.文章以STEAM教育理念为指导，将物理、数学、课程思政进行整合，基于北师大版八年级数学教材内容设计了一节初中“不等关系”的教学案例，在学习数学知识的过程中注入思想教育，将简单的概念教学生动化.

文中教学设计还采用了建构主义的5E教学模式与PBL教学法，引导学生在真实的问题情境中积极探索，发现新知，感受不同学科之间知识的联系性，注重发展学生的跨学科思维，培养数学意识，感悟数学精神.

3 数学案例教学设计

3.1 情境引入——创设问题情境

师：在上学期的物理课上，我们学习了如何用天平去秤物体的质量，今天的数学课我们也需要用到天平.首先请同学们回忆一下托盘天平的使用方法.

生：遵循“左物右码”的原则；游码要归于零刻度的位置；观察指针是否有偏移，是否需要调节平衡螺母，最终横梁要归于平衡.

师：很好，看来同学们学得很扎实.现在老师往天平的左盘放上一个铅块，右盘放上质量为30 g的砝码，游码依然在“0”的位置，请同学们观察一下，此时天平处于一个什么样的状态？

生：指针往左倾斜说明天平两边质量是不平衡的，铅块比砝码重.

师：同学们能否用符号表达出此时天平的不平衡关系？两边不平衡转化为数学形式应该用什么符号表达呢？

生：大于号或小于号.铅块质量>30 g.

师：同学们反应很快.铅块的具体质量我们并不知道，对于未知量可以将其设为x，天平两边不平衡关系的表达式就可以写为“x>30”.

设计意图：用托盘天平的平衡关系引出不等关系及其表达式，不仅能给予学生更为直观的感受，同时也可以让他们了解到数学与物理之间的跨学科联系，体会到知识的迁移，增强学生看待问题时的综合思维，打破思维定式.

3.2.活动探究——小组合作讨论

师：当我们用托盘天平进行物体质量的测量时，是利用等式性质来求物体的质量.当天平两边质量不平衡时，此时则是一种不等关系.我们刚刚也尝试将不等关系用数学符号表达了出来.现在请同学们仔细阅读表格(如表1)，小组同学之间展开合作讨论，完成以下两个活动.

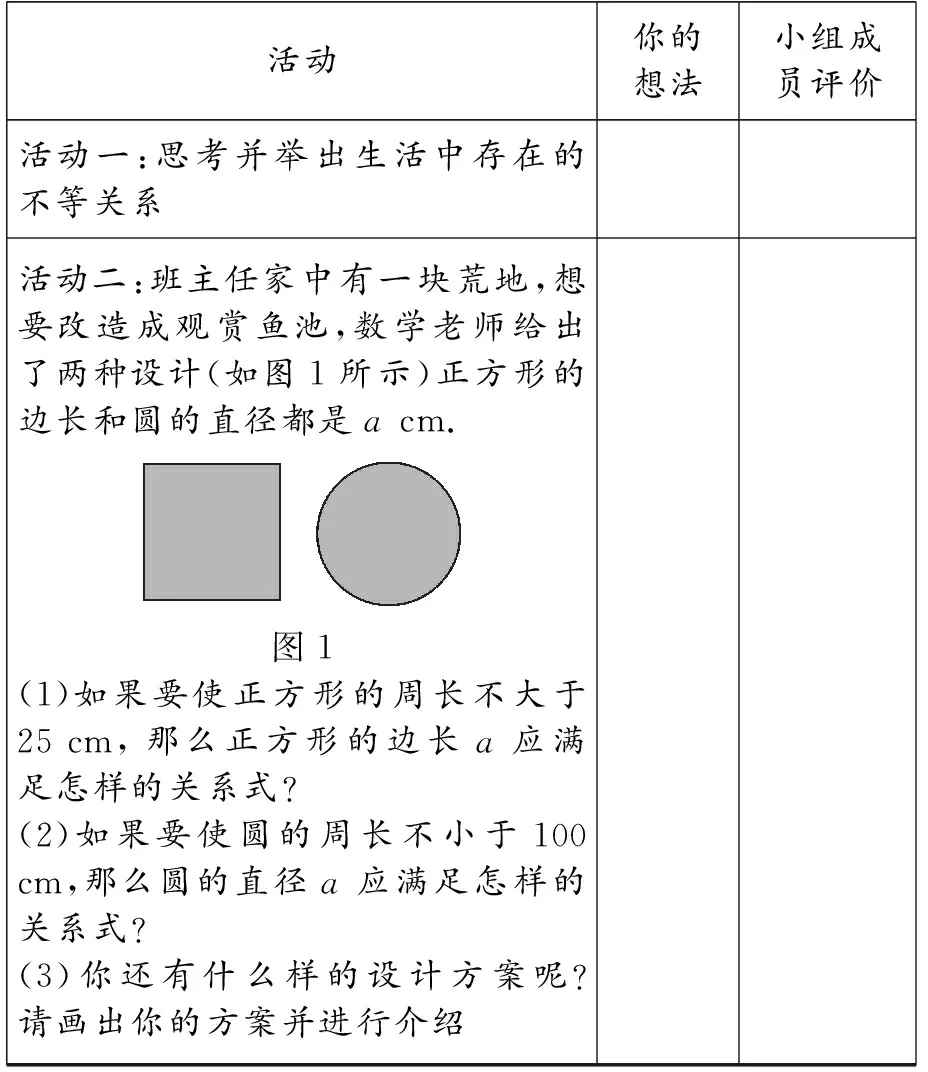
表1 活动记录表

设计意图：活动一让学生自行举例生活中存在的不等关系，并由同组同学评价举例是否合理恰当，加强学生之间的交流互动，同时也加深学生对于不等关系概念的理解.活动二选自北师大版八年级下册数学教材第二章第一节的引入部分并进行了改编，题目背景联系生活实际，更具有趣味性，题目答案更加开放以增强活动的探究性.在此活动环节，教师要引导学生认真参与，积极展开讨论，重视学生之间的互评并给予及时反馈.

3.3 概念解释——学生主体，教师主导

问题1拿出刚刚使用过的托盘天平，老师现在手上有三种形状不同的铅块▲，●，■，现在用天平称两次，其结果如图2、图3所示，若这三种铅块中球体的质量为50 g，请用关系式表达出▲和■的质量大小.

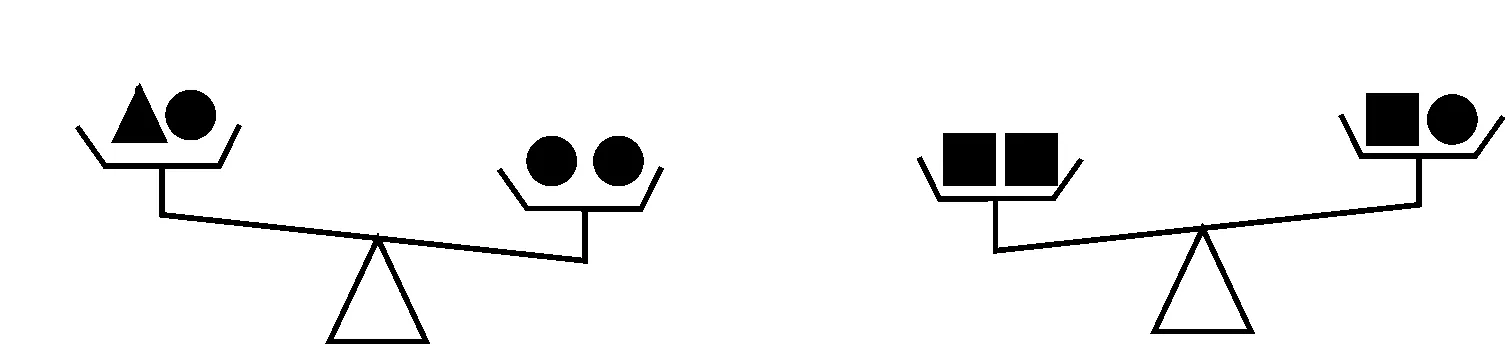
图2 图3

生:先设■的重量为xg，▲的重量为yg，根据天平的不平衡情况可以分别得出式子2x>x+50与y+50<100.

问题2铁路部门对于旅客随身携带的行李有如下规定：每件行李的长、宽、高三边之和不得超过160 cm.设行李的长、宽、高分别为acm，bcm，ccm，请你列出行李的长、宽、高满足的关系式.

生：a+b+c≤160.

师：仔细观察本节课已列出的关系式，它们有什么共同特点？

本环节中要给学生自由思考的时间，然后引导学生积极发言，总结出关于不等式的定义，特别注意学生对“不大于”“不小于”等词语的理解.对于学生自行总结的定义中的错误或不足之处，教师要给于提示.最后教师板书出关于不等式的标准定义：一般地，用符号“<”(或“≤”)，“>”(或“≥”)连接的式子叫做不等式(Inequality).

设计意图：问题1回到本节课开始时所创设的问题情境中，利用天平的平衡状态来比较物体质量的大小关系，跨学科的知识教学可以加强学科之间的横向联系，激发学生的求知欲望与探究精神，增强问题的趣味性，从而发展学生的学习迁移思维和能力；问题2则从学生们熟悉的铁路安检问题出发，更贴近生活实际.两个问题都要求学生列出具体的关系式，通过对已列出的表达式的观察，引导学生自行总结出不等式的定义，这一环节对于学生来说至关重要，教师要充分发挥主导作用.

3.4 概念精致——丰富知识，学会迁移

例1根据某市气象台“天气预报”报道，今天天气晴朗，最低气温为5 ℃，最高气温可达16 ℃，则今天气温t(℃)的范围是 ( ).

A.t>5

B.t<16

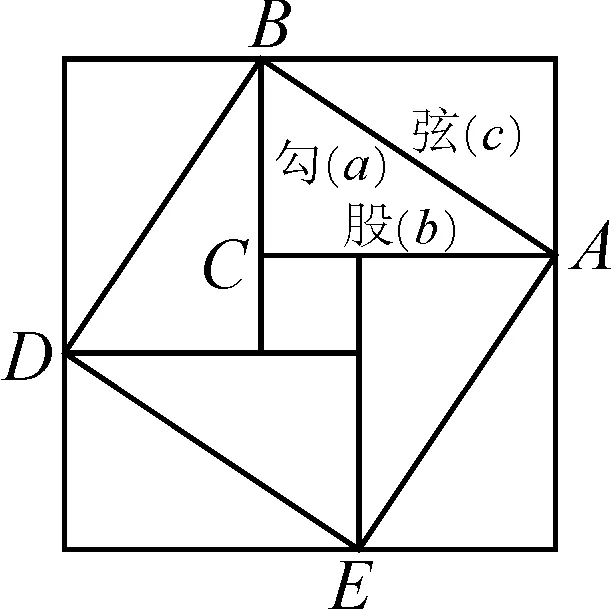
C.5

D.5≤t≤16

例2国际数学家大会是当前国际数学界规模最大也是最重要的会议.2002年第二十四届国际数学家大会在北京召开，这也是该会议第一次在发展中国家举办.会议标志(如图4)的设计基础源于1700多年前中国古代数学家赵爽绘制的弦图，他在勾股定理证明中所采用的“形数统一”“以形证数”思想，比西方的毕达哥拉斯早了五百多年.在八年级上册中我们也学习了勾股定理的证明与应用，现在请同学们仔细观察图5，小组同学之间进行讨论，找出图中存在的不等关系或不等式.

图4

图5

设计意图：例1以气温为背景设置问题，旨在使学生能够从实际的生活情境中抽象出不等关系并列出表达式，理解“最”字在日常生活中所蕴含的数学意义，感悟数学与生活之间的紧密联系.例2以第24届数学家大会的会徽为背景，展示了中国国际地位的提高，赵爽弦图的杰出贡献更是体现了中国古代人民的智慧.在数学教学的同时对学生进行思想政治教育，厚植学生的民族自豪感，培养学生的文化自信，以此激发学生的学习热情和奋斗意识.

3.5 课堂评价——总结评价，激励反馈

在本节课结束之际，教师要引导学生回顾整节课的学习内容，请学生自由发言，谈谈自己的收获和感受.学生的回顾不仅是课本内容的学习，也要注重对数学思想和课程思政的感悟和收获，更要体会到跨学科教学的积极作用.学生也可以提出自己的意见和对其他同学的评价，教师对于表现突出的同学也给予正面的表扬，发挥榜样的示范作用.

4 总结

STEAM教育进入课堂已经成为一种全球趋势，如何将STEAM教育本土化一直是近年来的热门教育话题.国内中小学的STEAM教育改革需要考虑到我国现实的教育资源、学生基础与教师水平，应结合现有的相关课程资源，在教学中逐步渗透STEAM教育理念，而不是一味地追求形式上的“好看”与“热闹”.本课题的教学设计采用STEAM教育理念，基于教材内容，利用已有素材进行跨学科整合教学，望为现阶段中学开发STEAM数学课程提供参考.