“用教材教”:提升基于教材的加工转化能力
——以人教版“二次函数”教材内容为例
⦿江苏省海安市城东镇西场初级中学 许海霞
1 引言
我们知道,很多专家都反对“照本宣科”,提倡“用教材教”[1].具体来说,教师要善于将教材内容加工为自己的教学内容,特别是转化为适合学生的学科教学活动.本文中结合人教版“二次函数”的教材内容,反思自己在加工转化为教学活动方面的一些实践和认识,以期抛砖引玉.
2 “二次函数”教学内容转化为教学活动的案例分享
案例(人教版九上教材)
活动1:(第54页“活动1”,改编设计.)
观察下列两行算式:
51×59,52×58,……,58×52,59×51
①
701×799,702×798,……,798×702,799×701
②
说明:①式两个乘数的十位上的数字都是5,个位上的数字的和等于10,两个乘数的和为110.
②式两个乘数的百位上的数字都是7,十位上的数字与个位上的数组成的数的和等于100.
活动设计:先组织学生观察①②式,请学生说出积最大的算式,(分别是55×55,750×750.)然后追问学生是如何发现积最大的这个算式.如果学生是“直接计算”后比较的,则追问其他学生有没有更好的方法.很可能学生会想到不同的方法,比如运用八年级学过的平方差公式来解释,也有学生可能会联想到运用二次函数的有关最值模型来解释.为了突出二次函数的应用价值,我们安排学生运用二次函数的知识说明它是正确的.
教法预设:以①式中55×55最大为例,设其中一个数为x,两个数的积为y,可得y=x(110-x)=-x2+110x=-(x-55)2+3 025.所以当x=55时,y取得最大值,即①式中,积最大的算式是:55×55.②式中750×750最大的证明,由学生独立练习然后再投影讲评.
有些学生在处理这类问题时思路比较开放,并不会局限于二次函数的视角.教师对于学生的不同方法应该表示肯定,但是需要引导学生从二次函数的角度进行解释,因为后续还有同类问题的变式跟进.
活动2:(第57页“第9题”,改编设计.)
如图1,点E,F,G,H分别在菱形ABCD的四条边上,AE=AH=CF=CG,连接EF,FG,GH,HE,得到四边形EFGH.设AB=18,∠ABC=120°,当AE为何值时,四边形EFGH的面积最大?
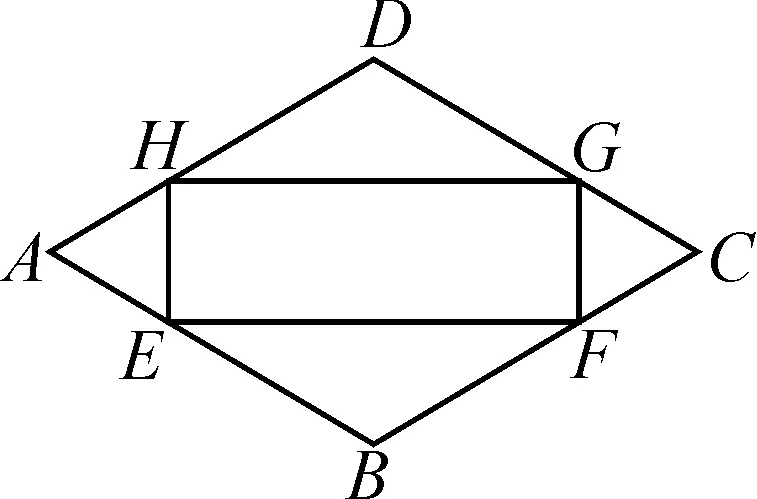
图1

图2
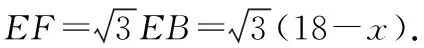
设计意图:学生在处理上述问题时可能会跳过证明四边形EFGH是矩形.但这一步是关键步骤,要提醒学生完善证明,然后再设参数,建议用二次函数模型,配方求最值解决问题.在解出答案之后,要引导学生解后反思,揭示出问题的深层结构:当点E在AB边中点时(点F,G,H分别是各边中点),四边形EFGH的面积最大.这个问题讲评之后,还可对问题进行“变式再练”(如果课堂教学时间不够,可以作为作业布置学生课后巩固),促使学生对这类问题的深刻理解.
变式再练如图3,在四边形ABCD中,∠B=∠D=90°,∠BAC=∠DAC=30°,矩形EFGH的顶点分别在四边形ABCD的四条边上,且AE=AH.若AB=6,当AE为何值时,四边形EFGH的面积最大?

图3
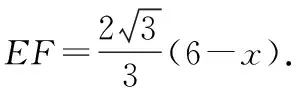
3 关于教材内容转化为教学活动的进一步思考
第一,教材上“过渡引言”可转化为教学活动.
人教版教材上在每章或每小节新知引入之前都会有一段“过渡语”或“新知引言”,这类“过渡引言”是教材编写专家精心编写的,值得师生认真体会其用意[2].教师可深入解读这些“过渡引言”的价值,并将其加工转化为教学活动,向学生传递好的学习方法.例如人教版“22.2二次函数与一元二次方程”这一小节就有这样的“过渡引言”:
“以前我们从一次函数的角度看一元一次方程,认识了一次函数与一元一次方程的联系.”
这段引言的教学价值在于引导学生学会类比旧知学习新知,对教师而言,可以将这段引言进行转化加工为开课教学活动,以下是笔者给出的教学设计:
问题1在八年级学习一次函数时,曾学习过从一次函数的角度看一元一次方程,请举例说明一次函数y=2x-1与一元一次方程2x-1=0的联系;
问题2类似地,二次函数y=x2-1与一元二次方程x2-1=0之间有怎样的联系呢?
为了让学生对一次函数与对应的一元一次方程之间的联系有更“具体”“直观”的旧知记忆,我们直接举例一次函数y=2x-1和一元一次方程2x-1=0,这样学生就可以直接从函数图象(直线)与x轴公共点横坐标和方程的解之间的对应关系来说明它们之间的联系;进一步再变式成为简单的二次函数y=x2-1与一元二次方程x2-1=0之间的联系,学生会很容易想到从函数图象(抛物线)与x轴公共点横坐标和方程的根之间的联系.
第二,教材上“标签备注”可转化为教学活动.
人教版教材上在还有很多“标签备注”和“云图备注”,也是值得教师在备课时重视的,笔者以为这些“标签备注”大多可以加工转化为教学活动.还以“22.2二次函数与一元二次方程”这一小节为例,其中有一个“标签备注”内容是:
“反过来,由一元二次方程的根的情况,也可以确定相应的二次函数的图象与x轴的位置关系.”
这个“标签备注”可以进行以下加工,转化为教学设计:
问题3我们知道,“数形结合”是重要的数学研究方法,刚刚我们从抛物线y=x2+x-2与x轴公共点的横坐标,得出相应方程x2+x-2=0的根,这体现了“由形得数”的方法.反过来,同学们能否由一元二次方程x2+x-2=0的根的情况确定相应的二次函数y=x2+x-2的图象与x轴有怎样的位置关系呢?
问题4我们在八年级曾经学习过“完全平方式”的概念,请举一个关于x的二次三项式恰为“完全平方式”的例子.
教学组织:这是一个开放式问题,比如学生举出一个完全平方式x2+4x+4之后,教师跟进追问,它所对应的一元二次方程x2+4x+4=0的根有什么特点?它所对应的二次函数y=x2+4x+4图象与x轴有怎样的位置关系?进一步,促使学生归纳出一元二次方程根的判别式“Δ”可以用来判定相应的二次函数的图象与x轴的位置关系.促使学生感悟“从特殊到一般”“从具体到抽象”的数学思想方法.
第三,教材上“经典习题”可转化为教学活动.
教材上的例、习题都是精挑细选过的,值得教师组织解题教学时重视和运用.特别是,教材上有些例、习题限于教材呈现的篇幅与难度控制,并没有给出变式或拓展,但教师可以根据自己任教班级的学情进行加工改编.比如上文提到的“活动2”只是给出一种变式再练,如果学生整体学情较好,还可将问题“一般化”,给出以下变式拓展问题.
“活动2”变式如图4,矩形DEFG的顶点均在△ABC的边上,当点D位于边AB什么位置时,矩形DEFG的面积最大?
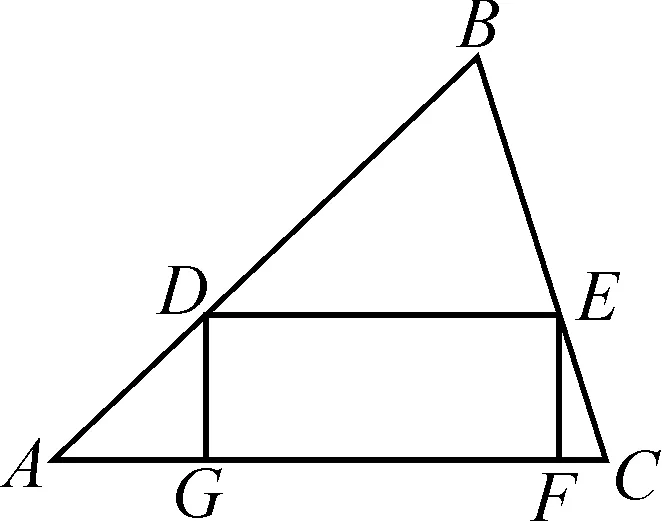
图4
“活动2”拓展如图4,平行四边形DEFG的顶点均在△ABC的边上,求证:平行四边形DEFG的面积不超过△ABC的面积的一半.
4 写在最后
教学设计能力是每一个教师需要终身修炼的教学基本功.而深入研读教材,重视教材内容的解读,并将其加工转化为教学活动,则又是专业基本功的显现[3].本文是笔者近期在二次函数教学后的一些实践反思,抛砖引玉,期待同行在研读教材和“加工转化”方面的更多实践成果.

