线段之妙 彰显数学之美
⦿湖北省利川市教学研究和教师培训中心 罗仁义⦿湖北省利川市建南镇民族初级中学 李小勇
1 原题呈现

图1
(2019年恩施州中考第23题)如图1,在⊙O中,AB是直径,BC是弦,BC=BD,连接CD交⊙O于点E,∠BCD=∠DBE.
(1)求证:BD是⊙O的切线;

2 试题感悟
题目中由条件“过点E作EF⊥AB于点F,交BC于点G”给出的线段EF,在解题时的作用妙不可言,彰显了数学之美,是本题的“点睛之笔”.其原因有三:其一,这条线段EF虽然在第(2)问中才出现,但它可以作为第(1)问中的辅助线,为第(1)问的证明拓展了思路,学生可以选用“垂径定理”“圆周角定理”“圆弧、圆周角、圆心角之间的等对等关系”等圆的基本性质来完成.其二,由于线段EF与BC相交于点G,第(2)问中要求的线段BG就是△BEG或者△BGF的边,如果选择用△BEG来求线段BG的长,就用“相似三角形”的知识来解决问题;如果选择用△BGF来求线段的长,就用“勾股定理”的知识来解决问题.其三,由于线段EF的出现,图形中又出现了一个等腰三角形CEG和几组相似三角形(如:△BGE∽△BEC,△CGE∽△CBD,△GEC∽△EDB,△DEB∽△DBC)和一组直角三角形(Rt△BEF与Rt△BGF).
在考试过程中,考生充分展示了他们的数学素养:考生用他们熟悉的“圆的基本性质”来找角的关系,用等角对等边来确定线段的长度,用相似三角形找比例关系,用勾股定理列方程,熟练地进行计算,准确地解方程,规范地书写答题过程.此题在实现考查和选拔功能的同时,也为考生提供了广阔的思维空间;在考查学生数学知识的整合能力、探索解题过程的思维品质的同时,也为初中数学教学起到了很好的导向作用.此题根植于教材,又高于教材,是一道好题.
3 考生的解题赏析
3.1 第(1)问的解法赏析
思路一:利用直径构建直角.

图2
解法1:如图2所示,连接AE.
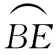
∴∠A=∠C.
∵∠BCD=∠DBE,
∴∠A=∠DBE.
∵AB是⊙O的直径,
∴∠AEB=90°.
∴在△ABE中,
∠EAB+∠EBA=90°.
∴∠DBE+∠EBA=90°,即∠DBA=90°.
∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:这是命题组给出的参考答案,思路直接,过程简洁.)
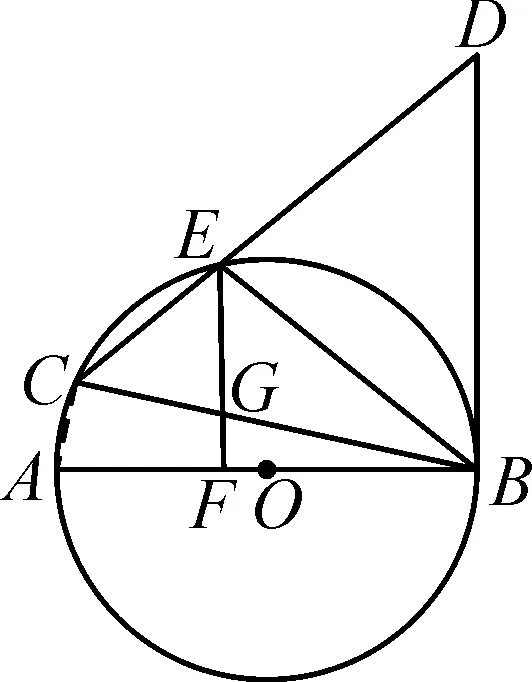
图3
解法2:连接AC,如图3所示.
在△DBE与△DCB中,有

∴△DBE∽△DCB.
∴∠DEB=∠DBC.
又∵四边形ABEC是⊙O的内接四边形,
∴∠DEB=∠A,
∴∠DBC=∠A.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴在△ABC中,∠A+∠CBA=90°,
∴∠DBC+∠CBA=90°,即∠DBA=90°.
∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:这里用到了圆内接四边形的性质,反映出教师在教学过程中对这个基本性质进行了拓展.)

图4
解法3:如图4所示,连接EO并延长,交⊙O于点M,再连接BM,则EM是⊙O的直径,
∴∠EBM=90°.
∴在△EBM中,
∠M+∠BEM=90°.
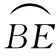
∴∠M=∠C.
又∵∠C=∠DBE,
∴∠M=∠DBE.
∵BO=EO,
∴∠OEB=∠OBE.
∴∠DBE+∠OBE=∠BEM+∠M=90°,
即∠DBA=90°.
∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:这种解法就是解法1的“翻版”,略显复杂.考生在答题时能够想到这种方法,但为什么没想到连接AE呢?反映了考生的紧张心态.事实上,在解法2的基础上,也可以进行类似的翻版,只不过更复杂,因此不可取.)
思路二:利用第(2)问“过点E作EF⊥AB于点F”的提示来解答.

图5
解法4:延长EF交⊙O于点H,如图5所示.
∵在⊙O中,AB⊥EH,
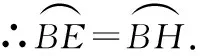
∴∠BCE=∠BEH.
又∵∠BCD=∠DBE,
∴∠BEH=∠DBE.
∴EF∥BD.
∵EF⊥AB于点F,
∴BD⊥AB于点B.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:这种解法把第(2)问中的“过点E作EF⊥AB于点F”作为第(1)问解答的辅助线,这也是此题的巧妙之处,给考生提供了更多的解题思路.有的考生利用这个提示,进行了较为复杂的角的转换,虽然可以达到解题的目的,但不可取.)
思路三:利用圆弧的度数来解答.
解法5:如图1,
∵AB是⊙O的直径,

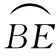
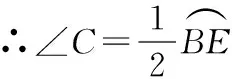
∵∠BCD=∠DBE,
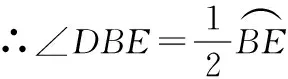


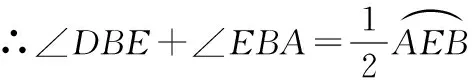
∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:考生的这种解法反映出教师在教学过程中补充了圆弧的知识,拓展了学生的解题思路.)

图6
解法6:连接EO,如图6所示.
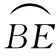
∵∠BCD=∠DBE,
∵BO=EO,
∴∠OEB=∠OBE.
在△BOE中,∠BOE+∠BEO+∠EBO=180°,
∴∠DBE+∠EBO=90°,即∠DBA=90°.
∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
解法7:连接EO,如图6所示.
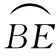
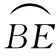
∵∠BCD=∠DBE,


∴AB⊥BD.
又∵AB是⊙O的直径,
∴BD是⊙O的切线.
(说明:这两种解法与参考答案,即与解法一有异曲同工之妙,也有考生在此基础上过点O作BE的垂线,同样可以解决问题,只是略显复杂.)
3.2 第(2)问的解法赏析
思路一:利用三角形相似求解.
解法1:如图1所示,
∵在△BCD中,BC=BD,
∴∠C=∠D.
∵∠BCD=∠DBE,
∴∠D=∠DBE.
∵EF⊥AB于F,
∴∠EFA=90°.
∵∠DBA=90°,
∴EF∥BD.
∴∠CEG=∠C,∠DBE=∠BEG.
∴CG=EG=3.
又∵∠BCD=∠DBE,
∴∠BEG=∠C.
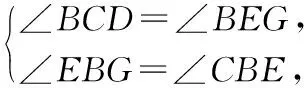
∴△BEG∽△BCE.
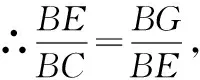
解方程,得BG=5或-8(舍去).
因此,BG的长为5.
(说明:这是命题组给出的参考答案,过程简洁,但考生的思维还是不容易达到这个高度.)
解法2:如图1所示,
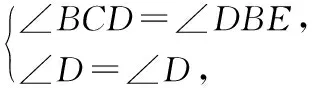
∴△DBE∽△DCB.
即BD2=DE·DC
∵EF⊥AB于点F,
∴∠EFA=90°.
∵∠DBA=90°,
∴EF∥BD.
∴∠CEG=∠D.
又∵BC=BD,
∴∠C=∠D.
∴∠C=∠CEG.
∴CG=EG=3.
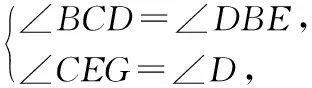
∴△GEC∽△EDB.
∴BD2=40+3BD.
解这个方程,得BD=8或-5(舍去).
因此BG=BC-CG=8-3=5.
所以,BG的长为5.
思路二:利用勾股定理求解.
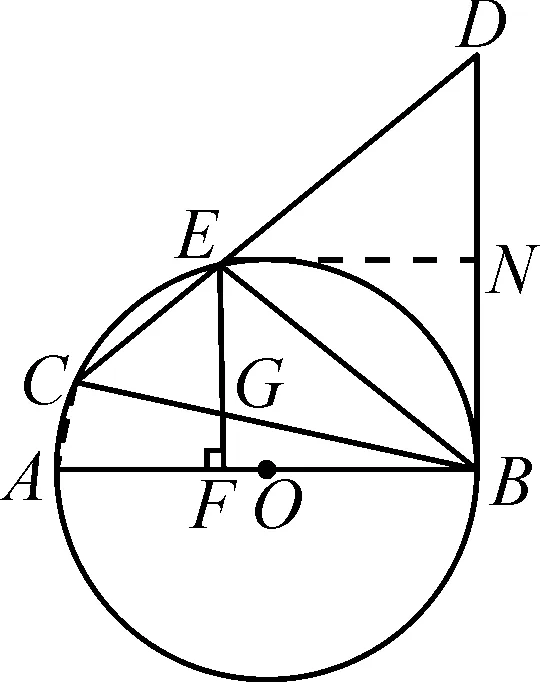
图7
解法3:如图7所示,过点E作EN⊥BD于点N.
由BC=BD,得∠C=∠D.
∵∠BCD=∠DBE,
∴∠D=∠DBE.
∵EF⊥AB于点F,
∴∠EFA=90°.
∵∠DBA=90°,
∴EF∥BD,
∴∠CEG=∠D.
∴∠C=∠CEG.
∴CG=EG=3.
∴BD=BC=BG+3.
在△BED中,BE=ED,EN⊥BD
在Rt△BEF中,有
在Rt△BGF中,有
整理,得BG2+3BG-40=0.
解这个方程,得BG=5或-8(舍去).
因此,BG的长为5.
解法4:延长EF交⊙O于点H,连接BH,如图8所示.

图9
∵在△BCD中,BC=BD,
∴∠C=∠D.
∵∠BCD=∠DBE,
∴∠D=∠DBE.
∵EF⊥AB于点F,
∴∠EFA=90°.
∵∠DBA=90°,
∴EF∥BD.
∴∠CEG=∠C.
又∵∠C=∠H,∠CEG=∠GBH,
∴∠H=∠GBH.
∴GB=GH.
∵在⊙O中,AB⊥EH,
∴EF=HF.
∴BG=HG=HF+GF=EF+GF=3+2GF.
在Rt△BEF中,有
在Rt△BGF中,有
BF2=BG2-GF2=(2GF+3)2-GF2.
整理,得2GF2+9GF-11=0.
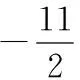
∴BG=3+2GF=3+2=5.
因此,BG的长为5.
(说明:题目给考生提供了广阔的思维空间,考生给出了多种不同的解答方法.线段EF,妙!)
4 教学启示
首先,教学必须立足课本.用教材进行教学的关键是把知识的脉络理清楚.针对课本中的基本概念、性质、定理、基本图形,学生不仅要知其然,还要知其所以然;不仅要“会用”,还要弄清楚知识的来龙去脉,深刻理解知识的本质.认真研究和挖掘课本中习题的深层次价值,挖掘概念的内涵和外延,归纳总结重要图形和方法,并尝试做一些拓展,发挥出课本的最大价值.几何综合题的教学要狠抓基础(基本图形、基本知识、基本方法等),积极渗透数学思想方法,培养学生分析问题、解决问题的能力.同时,还要培养学生的独立思考能力:怎么去思考问题,怎么去找突破口,为什么这样,为什么不这样,还有更好的方法吗……
其次,注重发展学生的推理能力.《义务教育数学课程标准》中明确指出:“要培养学生的运算能力、发展逻辑思维能力.”因此,培养学生的能力,特别是逻辑推理能力是初中数学教学的核心,也是推进素质教育的一个重要手段.我们要加强对数学教学现状的反思和对“新课标”的学习,在课堂教学中落实合情推理与演绎推理并重的教学思路,力求让学生在知识获得的过程中有所悟,从而了解知识的来龙去脉和内在联系,形成对数学的真正理解,为学生的继续学习提供条件.
最后,欣赏完考生们的各种解题方案,感觉真是八仙过海,各显神通,美不胜收啊!我们为师者,不能局限于传道、授业、解惑,而是要善于利用数学之美,激励和唤醒学生,鼓励他们做学习的主人.

