例谈构造函数法在高考导数题中的应用*
⦿山东省滨州实验中学
王汉芹 刘玉华
《普通高中数学课程标准(2017年版)》指出:“对于较复杂的数学问题,能够通过构建过渡性命题,探索论证的途径,解决问题.”构造函数就是提出假设和引理的有效途径之一.但构造函数对学生的综合能力要求较高,考查学生对函数与方程、转化与化归、数形结合思想的深度理解.教学实践发现,多数学生不知道如何构造函数,要么走不少弯路,要么不知如何下手.因此,笔者围绕2020年和2021年新高考全国Ⅰ卷导数题构造函数问题展开研究,得到构造函数的常见题型和方法,以提高学生构造函数解决问题的能力,发展数学抽象、逻辑推理等数学素养.
1 同构法构造函数
所谓同构法构造函数,就是等式或不等式经适当整理后可以表示成两侧结构相同的式子,利用这个结构式构造对应函数,再用函数性质解决问题的方法.下面以2020年新高考全国Ⅰ卷第21题来说明这个方法.
例1(2020年新高考全国Ⅰ卷第21题)已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
解析:(1)略.
(2)不等式f(x)≥1,即aex-1-lnx+lna≥1,其中x>0,a>0.
即elna+x-1-lnx+lna≥1.
即elna+x-1+lna+x-1≥x+lnx.
即elna+x-1+lna+x-1≥elnx+lnx.
设g(x)=ex+x,x∈(0,+∞).
因为g′(x)=ex+1>0,所以g(x)在(0,+∞)单调递增.
因为elna+x-1+lna+x-1≥elnx+lnx,所以
g(lna+x-1)≥g(lnx).
因为g(x)在(0,+∞)单调递增,所以
lna+x-1≥lnx,即lna≥lnx-x+1.
然后再求lnx-x+1(x>0)的最大值即可.
本题先得到同构式elna+x-1+lna+x-1≥elnx+lnx,再构造函数g(x)=ex+x,x∈(0,+∞),再利用函数g(x)的单调性,得到关于a的简单不等式,从而求解.同构式的获得,就是学生观察、分析、变形、构造的过程,这是一个从无到有的过程,可以提高学生发现问题、观察问题、分析问题和解决问题的能力,发展数学抽象、逻辑推理等核心素养[1].
指数对数混合问题同构式构造函数主要有以下几种模型[2]:
(1)和差型(ea±a≥b±lnb).
①ea±a≥elnb±lnb⟹g(x)=ex+x;
②ea±lnea≥b±lnb⟹g(x)=x+lnx.
(2)积型(aea≥blnb).
①aea≥(lnb)elnb⟹g(x)=xex;
②ealnea≥blnb⟹g(x)=xlnx.
这是本题变形成同构式时,用到的两个模型.常用的同构式除了和差积型之外,还有商型.
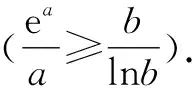
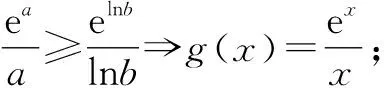
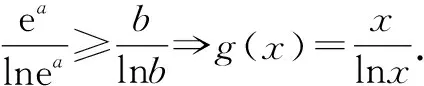
所以,在教学中,教师要引导学生总结指数对数混合问题常用函数模型.养成勤思考、善总结的好习惯,发展数学建模、逻辑推理等数学素养.
高考题中的导数题,经常有对同构法构造函数法的考查,例如下面这两道高考题和例1类似.
题1(2018年全国卷Ⅰ文第21题)已知函数f(x)=aex-lnx-1.
(1)设x=2是f(x)的极值点,求a,并求f(x)的单调区间;
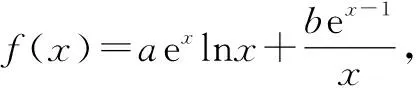
(1)求a,b;
(2)证明:f(x)>1.
2 放缩法构造函数
例1的第(2)问还可以利用放缩法构造函数解不等式.放缩法构造函数,是对函数进行放缩来证明不等式,常用于指数或对数的不等式问题中.常用的放缩函数有:ex≥x+1(x∈R,当x=0时等号成立),lnx≤x-1(x>0,当x=1时等号成立),以及由两者衍生出来的其他形式.
本题根据aex-1-lnx+lna≥1,利用两次放缩ex-1≥x,ln(ax)≤ax-1,并且等号同时成立的条件都是x=1且a=1.这样就能证得a≥1.
放缩法证明指数或对数不等式问题,在高考题中也是层出不穷,如前面题1(2018年全国卷Ⅰ文第21题)也可以运用放缩法求解.题3亦是.
题3(2013年全国新课标Ⅱ卷理第21题)已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)≥0.
2020年新高考全国卷Ⅰ第21题,体现了构造函数的两种方法,同构法构造函数和放缩法构造函数,与解决此题的常规方法——隐零点法对比,这两种方法更简洁,所以构造合适的函数可以达到事半功倍的效果.无独有偶,2021年新高考全国卷Ⅰ第22题也用到了构造函数法.
3 消元法构造函数
3.1 利用f(x1)=f(x2)消元
例2(2021年全国新高考Ⅰ卷第22题) 已知函数f(x)=x(1-lnx).
(1)讨论f(x)的单调性;
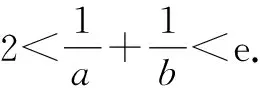
解析:(1)略.
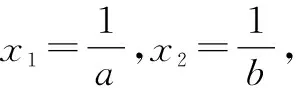
由(1)及f(x1)=f(x2),得0 要证2 2-x1 又因为f(x)在(1,+∞)单调递减,所以即证 f(2-x1)>f(x2)>f(e-x1). 即证 f(2-x1)>f(x1)>f(e-x1). 所以,构造函数 g(x)=f(x)-f(2-x)(0 h(x)=f(x)-f(e-x)(0 分别利用导数证明以上两个不等式即可. 此方法是利用双变量函数值之间的关系,进行消元.这里需要根据要证明的变量不等式构造函数,根据函数的单调性得到函数值之间的关系,进而利用函数值的关系消元. 3.2 引入新变量消元[3] 例2的第(2)问还可以引入新变量消元,消元之后再构造函数. 代入blna-alnb=a-b,得 bln(bt)-btlnb=bt-b, 即证ln2 3.3 直接代入消元 (1)讨论f(x)的单调性; 本题第(2)问根据x1x2=1的关系式,直接用x2表示x1,从而消去x1. 3.4 整体换元消元 (1)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln2; (2)略. 本题第(1)问将f(x1)+f(x2)表示成关于x1x2的式子,然后整体换元消元. 3.5 确定主元消元 例5(2020年天津高考第20题)已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数. (1)略; 解析:(1)略. (2)题设不等式等价于(x1-x2)[f′(x1)+f′(x2)]-2[f(x1)-f(x2)]≥0. 以x1为主元,构造函数h(x)=(x-x2)[f′(x)+f′(x2)]-2[f(x)-f(x2)]≥0. 因为x>x2≥1,且h(x2)=0,所以只需利用导数证明h(x)在(x2,+∞)单调递增即可.证明过程略. 本题观察要证明的式子,其中x1和x2是对称出现的,所以确定x1或x2为主元,从而构造函数h(x). 以上是基于新高考Ⅰ卷2020年和2021年导数压轴题得到的构造函数的主要方法.如何攻克构造函数问题呢?笔者提以下几点建议供同仁们参考. 第一,重基础.学生掌握好基础知识、基本技能、基本思想方法是灵活构造各类函数的基础.因此,在教学中,要下大力气夯实基础,抓好函数基本性质的复习. 第二,重思想.数学思想方法是数学的灵魂.在教学中,要加强数学知识之间的前后关联,重视数学思想方法的运用和渗透,提升学生数学思维能力. 第三,重实战.用构造函数法解决问题,需要细心观察、类比联想与变形转化,尽量构造易求导的函数.这种数学思维方法需要不断强化训练,才能灵活解决问题. 第四,重讲解.教师应精选题目,对此种类型的题目进行前挂后连、纵横联系,不断总结构造函数的规律,积累构造函数的方法,促进学生解题能力的进一步提升. 总之,我们要让学生学会构造函数解决导数综合题的方法,在解题过程中大胆变形,小心求证,提高解决综合性和创新性问题的能力.
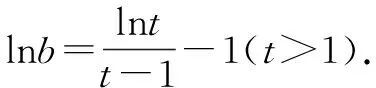
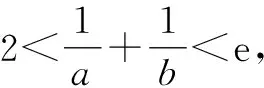
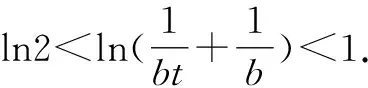
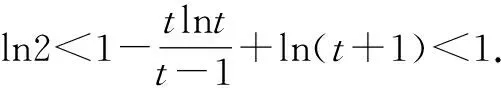
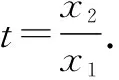
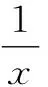
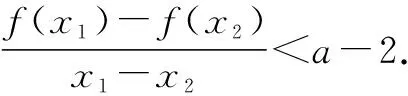
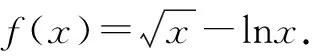
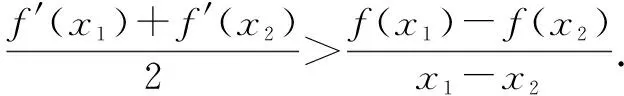
4 几点建议

