“七彩阳光”2022届新高考研究联盟
——道试题的探究
⦿甘肃省张掖市临泽县第一中学
刘 义
1 引言
解三角形问题能自然合理交汇与融合代数关系式变换,以及函数与方程、三角函数、平面几何与平面解析几何、基本不等式、导数等相应的数学基本知识,背景简洁明了,思想方法丰富,技巧策略多样,能很好考查考生的数学基础知识、思想方法和数学能力,提供考生更多的机会与空间,充分展现学生的能力水平,倍受各方关注.
2 问题呈现

本题是一道涉及解三角形的最值的综合应用问题,通过给出三角形的面积,求解涉及三角形三边的代数关系式的最值.此类问题是近几年高考数学试卷中的一个热点,主要考查解三角形的相关知识,如正弦定理,余弦定理,面积公式等,同时交汇三角函数、基本不等式、函数与方程、导数等相关问题.
3 问题破解
思维视角一:三角函数思维.




点评:根据题目条件,结合三角形的面积公式加以转化,通过正弦定理化边为角的关系式,利用所求代数关系式的通分以及恒等变换,结合余弦定理与正弦定理转化为角的关系式,利用辅助角公式变形,利用三角函数的图象与性质确定最值.

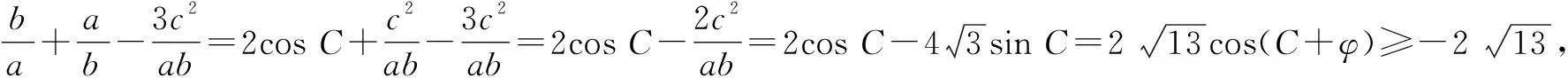


点评:根据题目条件,结合三角形的面积公式加以转化,通过余弦定理的应用与关系式的变形,从另一角度将所求的代数关系式转化为同一角的三角函数关系式,结合辅助角公式的应用,利用三角函数的图象与性质确定最值.利用代数关系式的特征,巧妙合理变形,从而实现等量代换与变形,思维视角不同,方法技巧类似.

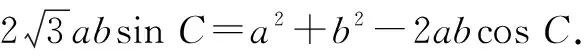




点评:根据题目条件,结合三角形的面积公式加以转化,通过余弦定理的应用与关系式的变形,同样可以将所求的代数关系式转化为同一角的三角函数关系式,结合辅助角公式的应用,利用三角函数的图象与性质确定最值.不同的公式应用与视角切入,抓住化边为角,转化为同一三角函数关系式,进而利用三角函数的图象与性质确定相应的最值.
思维视角二:坐标思维(坐标法).




根据基本不等式,可得
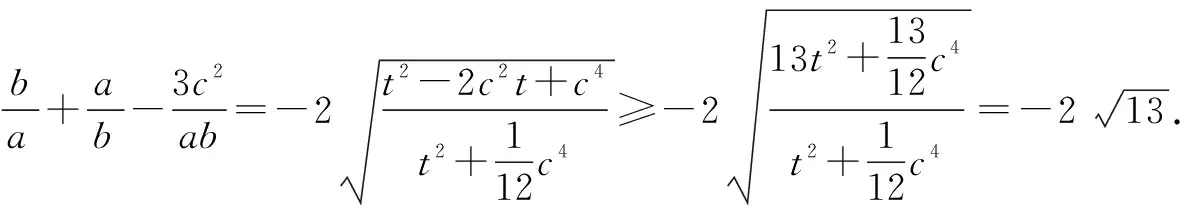


点评:通过构建平面直角坐标系,结合点的坐标,利用三角形的面积公式确定点C的坐标,通过两点间的距离公式的应用,通过关系式的恒等变形以及换元处理,利用基本不等式来确定相应的最值.
思维视角三:函数思维(导数法).

化简整理得4c4-6(a2+b2)c2+3(a2-b2)2=0,解得






点评:利用海伦公式用边的关系式来表示三角形的面积,通过关系式的转化,构建涉及c2的方程并加以求解,进而用涉及另两边的关系式来表示所求的代数关系式,通过换元处理,构建对应的函数,利用函数求导,结合导函数的零点来确定对应函数的最值.利用导数法求解最值时,关键是构建对应的函数,合理地换元处理为导数法求解提供条件.
4 变式拓展
探究1保留题目创新情境,简化求解代数式,使得问题更加简单快捷,难度中等偏下,较原题难度有所下降,比较适合大部分同学.




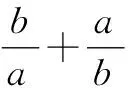
故填答案:4.
探究2保留题目创新情境,改变代数关系式,化减号为加号,从最值的另一个角度来求解,知识点考查的难度与原题相当,难度中等.





5 解后反思
(1)思路归纳,策略总结.
解三角形问题的一般思路有以下两种:①代数角度,利用正、余弦定理,寻找关于角或者边的关系进行合理化简.有时也可通过建立平面直角坐标系,将问题转化为函数最值问题进行求解.②几何角度,借助平面几何知识,寻找图形中蕴藏的几何关系,结合逻辑推理、数学运算等来分析与求解.
(2)最值问题,方法担当.
破解解三角形有关的求值与最值问题,关键是对已知条件的分析,从代数角度切入,将边角关系利用正、余弦定理进行转化.利用正弦定理化角,往往会结合三角恒等变换公式以及辅助角公式,转化为三角函数的值域问题;利用余弦定理化边,往往结合基本不等式和三角形三边关系进行求解;利用平面几何图形的变化规律,通过极端思维或端点效应来确定相应的最值问题.

