“数形结合思想”复习课的单元教学设计*
⦿衡阳师范学院数学与统计学院
聂 静 彭嘉瑶 罗振国 罗李平
1 引言
《普通高中数学课程标准(2017 年版)》[1]从教学设计和实施的几个主要环节提出了数学教学建议,而落实这些建议的关键是实施单元教学.单元教学强调基于整体视角重构知识体系,防止知识教学碎片化,要求教师将零碎的知识以本身的逻辑关系或者数学思想方法进行分析、重组与整合,以促进学生深化理解知识,把握数学本质,这对培养学生能力以及提高核心素养具有重要意义.近年来,以三角函数[2]、平面向量[3]、高中函数[4]、直线与平面平行[5]、数列[6]等知识本身的逻辑关系进行单元教学设计的理论和实践研究成果比较多,但很少涉及复习课.
《普通高中数学课程标准(2017 年版)》[1]同时指出复习课的复习题要关注单元知识的系统性,帮助学生理解数学的结构,增进复习的有效性,达到相应单元的“学业要求”.数形结合思想是高中数学的重要思想,它可以把抽象的数学语言与直观的图形结合起来,进行几何直观的分析与代数抽象的探索.本研究基于课程标准的要求,以复习课为视角,探索以数形结合思想为主线的高中数学复习课的单元教学设计.
2 数形结合思想涉及的知识内容
现对高中数学中涉及数形结合思想的知识点作以下梳理:函数与方程和不等式、集合中的Venn图、函数的单调性、函数的奇偶性、函数的最值、三角函数的概念、用三角函数解三角形、平面向量的概念与运算、复数的表示、解析几何中涉及的平行、垂直的证明与距离、角度的计算(以数解形)、导数的几何意义、简单的线性规划、几何概率等.
从数形结合涉及的知识点可以看出,数形结合思想几乎贯穿整个高中数学课程.
3 学情分析
学生在学习新知的过程中已经对数形结合思想涉及的各知识点有所理解,但由于高中数学知识高度抽象,可能对一些知识点的理解不够深刻;同时学生对数形结合思想有了初步体会,有的学生可能已经发现数形结合可以把抽象的问题直观化,但是更多的学生还是偏向于喜欢从小学就开始接触的代数法,缺少对数形结合思想的应用意识.
4 教学目标
下面摘录高中数学课程标准中涉及数形结合思想的部分知识点的教学目标要求.
(1)函数与方程和不等式:
借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系.
(2)函数的单调性、函数的最值:
借助函数图象,会用符号语言表达函数的单调性、最大值、 最小值,理解它们的作用和实际意义.
(3)三角函数的概念:
借助单位圆建立一般三角函数的概念,体会引入弧度制的必要性.
(4)复数的表示:
掌握复数的表示、运算及其几何意义.
(5)导数的几何意义:
通过函数图象直观理解导数的几何意义.
以上教学目标中都提到了借助图形或者几何意义理解相关知识点,渗透数形结合思想,学生在学习新课时已经有所把握.
现将以复习课为视角,以数形结合思想为主线的复习课单元教学设计的教学目标设定为:注重数形结合思想,培养数形结合意识,深化理解数学概念,提高解题的效率.
5 例谈数形结合思想单元教学设计的实施
下面结合学生的认知程度,从数形结合思想有利于学生深化理解数学概念和提高解题效率两个方面进行举例说明,引导学生从“形”的角度进行探究.
5.1 数形结合思想有利于深化理解数学概念
(1)利用数形结合思想深化理解函数单调性.
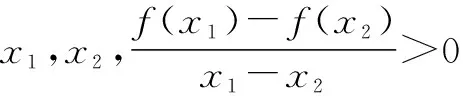
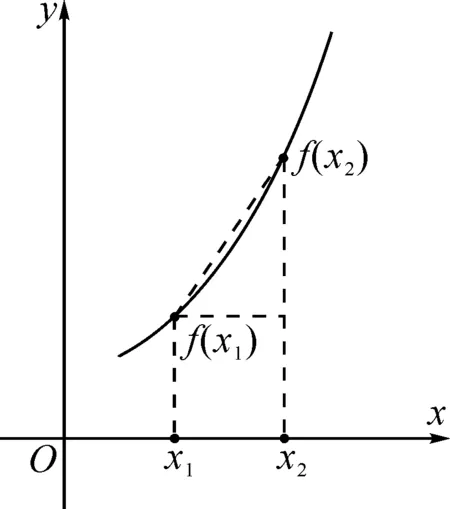
图1
(2)利用数形结合思想深化理解导数几何意义.
导数的概念涉及极限的思想,抽象性很强,甚至对于切线的概念学生都会感到很抽象,所以仅对导数的概念进行符号语言的描述,学生很难接受.也许在初学时记住了导数的几何意义是切线的斜率,但是,学生可能还达不到对其真正深入理解.
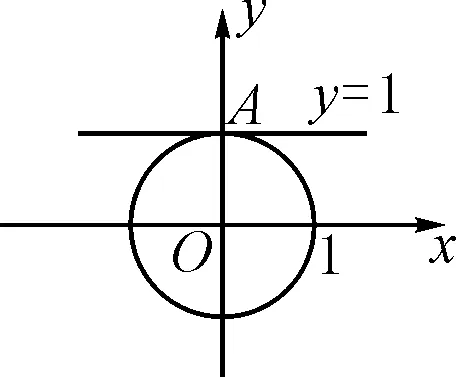
图2
如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切,学生对此结论很熟悉.如图2所示,过点A(0,1)作单位圆x2+y2=1的切线,学生很快可以给出这条切线的方程为y=1.
导数的几何意义是切线的斜率,现利用导数的定义与几何意义来推导单位圆在点A(0,1)处的切线方程,看是否与y=1一致.
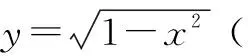
在x0=0处,由导数定义,得
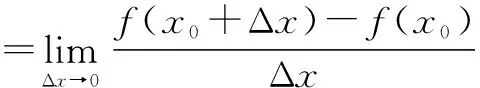
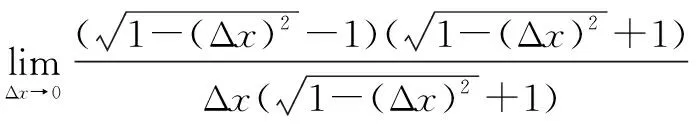
即f′(x0)=k=0.
学生利用导数的定义推导出单位圆在点A(0,1)处的切线斜率为0,从而利用点斜式得出单位圆在点A(0,1)处的切线方程为y=1.这与学生已知的“过点A(0,1)作单位圆的切线的方程为y=1”完全一致,从而使学生更深刻、更信服地理解导数的几何意义是切线的斜率.
(3)利用数形结合思想深化理解虚数单位i的含义及虚轴的产生.
学生已经学习了复数的概念与几何意义,但是很多学生仍然不理解i的含义,还有为什么y轴可以表示虚轴?现从图形上引导学生思考,进而深化理解.

图3
我们知道,实数与数轴上的点是一一对应的,如图3所示,我们用数轴上的点A表示实数b,b乘-1得到实数-b,-b在数轴上的对应点为点A′, 则点A′可以看作将点A绕原点O(逆时针)旋转180°所得[7].(下文提到的旋转均默认为逆时针旋转.)
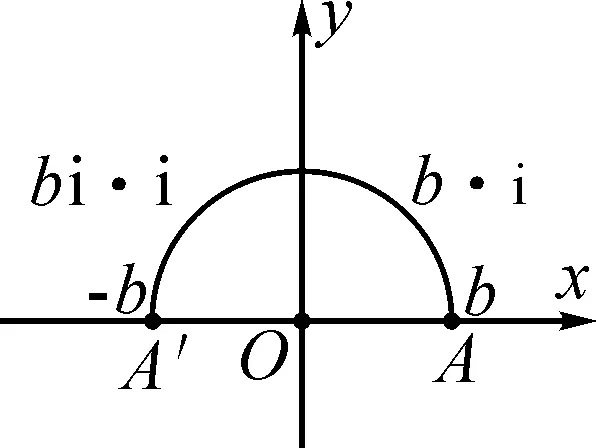
图4
由i2=-1,即i·i=-1,那么b·(-1)=b·(i·i)=b·i·i所对应的点可以看作将点A绕原点O连续作两次旋转90°所得[7].如图4所示,b·i所对应的点可以看作点A绕原点O旋转90°所得,那么bi所对应的点都可以在这条垂直于数轴的直线上,这样虚轴就产生了,使学生深化理解了为什么y轴可以表示虚轴.bi·i表示虚轴上的点再次旋转90°,即得到-b在数轴上的点A′.
这里利用数形结合思想使学生直观感知到虚轴是怎么产生的,并深刻理解了i的含义.
利用数形结合思想还可以深化理解三角函数的定义、向量概念与运算等,这里不再例谈.
5.2 数形结合思想有利于提高学生解题的效率
(1)利用数形结合思想,借助函数图象讨论方程的解的个数.
基本思想:先把方程两边的式子变成两个熟悉的函数表达式,然后结合图象进行分析.
例1已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0有4个互异的实数根,求a的取值范围.
分析:由f(x)=|x2+3x|,将f(x)-a|x-1|=0化为|x2+3x|=a|x-1|.令g(x)=a|x-1|,问题转化为两个函数图象的交点问题,即当函数g(x)与f(x)的图象有4个交点时,求a的取值范围.如图5所示,分别画出函数f(x)与g(x)的图象,利用函数图象直观地分析交点的大致情况,从而求出a的取值范围.

图5
(2)利用数形结合思想,借助复数几何意义解决复数相关问题.
基本思想:从题目所给式子的形式(适时变形),基于复数几何意义解题.
例2如果复数z满足|z+i|+|z-i|=2,那么|z+i+1|的最小值是多少?
分析:此题若是用代数方法设z=a+bi(a,b∈R),由于条件中含有两个绝对值,因此做起来会非常麻烦.引导学生利用数形结合思想与复数的几何意义去求解,会使问题变得简单.
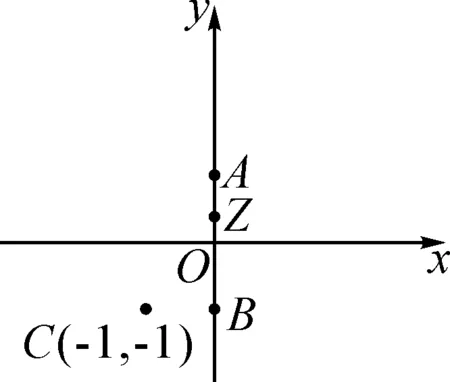
图6
如图6所示,设复数z,i,-i,-1-i分别对应复平面内的点z,A(0,1),B(0,-1),C(-1,-1).|z+i|可以看作是点Z到B的距离,|z-i|可以看作是点Z到点A的距离,|z+i|+|z-i|=2可以看作是点Z到点B与点Z到点A的距离之和为2,从而得到点Z在线段AB上;|z+i+1|的最小值可以看作点Z到点C的距离.由图形可以直观判断出:当点Z与点B重合时,点Z到点C的距离,即|z+i+1|的最小值为1.
(3)利用数形结合思想,借助解析几何中斜率、距离等几何意义解决最值问题.
基本思想:从题目所给式子的结构形式(或适当变形),利用式子的几何意义解题,充分利用数形结合思想.
例3已知实数x,y满足方程x2+y2-4x+1=0,求:
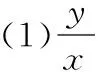
(2)y-x的最小值;
(3)x2+y2的最大值和最小值.
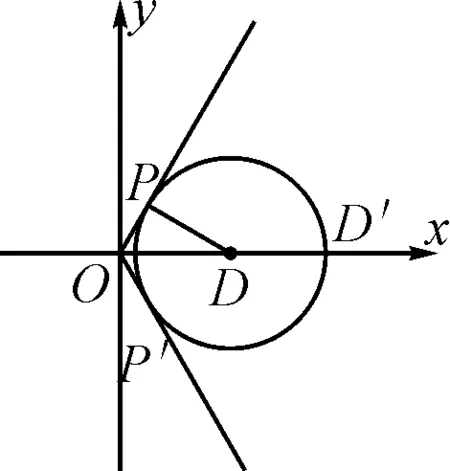
图7
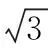
利用数形结合思想还可以解决线性规划、几何概率等问题,这里不再例谈.
6 评价与反思
以数形结合思想作为一个大单元进行教学设计,有利于提高学生的数形结合意识.以复习课的视角,基于学生已有的认知程度,举例说明了数形结合思想可以使学生深化理解比较抽象的数学概念,提高解决问题的效率,培养了学生的高阶思维能力,促进了核心素养的发展.

