基于提升数学核心素养的有效教学思考
——浅析“利用导数研究函数的最值”的教学设计
⦿江苏省苏州市吴中区苏苑高级中学
胡 莺
1 数学教学
“立德树人”是数学教育肩负的重任.高中新课程标准要求数学要培养学生用数学知识、方法和思维去观察、分析和探索世界. 高中数学的有效教学以学生为主体,贯彻有效的理念.高中数学教学要激发学生的学习热情,促进学生运用数学思维思考问题,以数学核心素养解决问题,实现个人可持续的发展.因此,高中数学的有效教学尤其重要.
学生在学习导数后,体验导数在研究函数中的应用,既及时巩固导数知识,也深化导数的工具作用. 同时导数的应用助力学生理解导数,培养学生的自主探索意识. 笔者安排高二文科班“利用导数研究函数的最值”教学,以实际教学设计,巧妙培养学生数学思维,提升数学核心素养.
2 实践探究
师:请大家思考下面的例1.
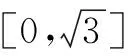
生1:对函数求导分析单调性,比较函数f(x)在区间上的极值和端点值的大小,最后得到值域.
(生1板演)令f′(x)=3-3x2>0,解得-1
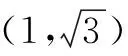
因此,f(x)在定义域上存在极大值f(1)=2.
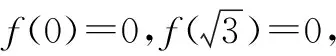
故函数f(x)的值域为[0,2].
师:如果以例1为题根,怎么进行变式呢?
(学生小组讨论,得到部分变式如下.)
变式1函数f(x)=3x-x3在[0,m]上的最大值为2,最小值为0,则实数m的取值范围是________.(生2提供的变式.)
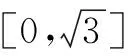
教学思考 :在例1教学中,学生将求函数的值域转化为利用导数求函数的最大值与最小值, 利用导数基础知识就能完成解答.学生口述解题想法是其理清思路的过程,板演的“书写”则进一步呈现逻辑思维.而在本例变式的小组讨论时,学生学习热情高涨,各抒己见,并且精神高度集中地“听”其他同学的想法,努力“读”懂新的数学思维.这一过程中,教师不应为了赶教学进度,挤压学生在课堂上“说”的时间. 著名心理学家皮亚杰提出:学生学习的知识是要通过自我建构得到的,而非依靠教师的一味讲授. 教师简明扼要的“说”,是引导问题、引发讨论,更是引导学生自主思考“大问题”,引导学生有效探究“新问题”. 本题变式为学生开启自由探索之门,引领学生走入探索之路;促使学生深入理解知识点,领悟单元联系,发展创新能力;落实有效教学,促使学生主动参与数学学习,提高数学抽象和逻辑推理素养.
师:由变式2在函数中引入参数,我们看下例2.
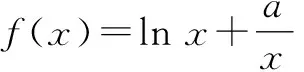
师:请同学们想一想怎么解?
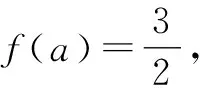
师:他的解答正确吗?(学生思考)
师:请考虑在定义域内研究.
生5:极小值点可能不在定义域内.
师:很好.那么能分哪些情况?
生5:若1 教学思考:例2是新高考的填空题题型,为学生应用导数研究函数搭建桥梁. 本题学生独立解答的完成度不高,但是学生运用分类讨论思想分析,基本方法计算,发现函数的最值在区间端点或极值点处取得,这是生生合作完善解答的结果. 在解题时,教师要肯定学生始于直觉的分析,鼓励学生基于思考的解答,是培养学生自信心,是数学课堂师生交流的真正开始.师生交流是以学生为主体的有效教学的主要体现,能打造和谐的师生关系,促进师生情感的增长,进而提高教学的有效性.本题旨在有效提高学生的思维品质,提升数学运算和逻辑推理素养. 师:下面继续研究含参数问题. 师:请比较例2和例3的变化. 生6:例2给出最值,例3是存在最值;两个例题的区间不同,一个是闭区间,另一个是开区间. 师:解题思路有何变化? 生6:没有变化.(学生摇头) 师:请尝试解答. 师:最值一般在哪里取到? 生6:区间端点或者极值点. 师:计算看看有什么发现? 生6:g(0)=3.又接不下去了. 师:怎样利用导数求函数的最值,关键是什么? 生6:关键是利用导数判断函数的单调性,看导数值的正负. 师:非常好.将上述解答中的g(x)与导数正负联系,接下来怎么解答?(学生互动讨论.) 师:非常棒!从例1到例3,你有什么收获? 生7:最值通常为区间端点函数值或者极值. 生8:函数解析式含参数常需要分类讨论. 生9:导数值正负是判断函数单调性的关键. 师:同学们在解题时敢想、敢说、敢写.同时要注意书写规范,养成良好习惯;及时总结,提高思维品质. 教学思考:例3进一步研究含参数函数的最值,学生通过归纳类比,发现问题变化,吸取例题经验,实现问题转化,找到解题突破点.教学中,教师引导学生总结思考,为学生后续的导数学习提供无限可能. 教师还应指导学生拓展阅读,这样,学生能扩充知识储备,拓宽解题视角,树立全局意识. 同时,高中数学的“写”需要延伸到课堂之外,师生的“写” 不仅有解答,还有思考总结.师生利用碎片时间,每天记录一点,日积月累就能成文分享. 本题在师生、生生互动中,促进思想交流,也使课堂变得灵动,实现有效教学,提高个人思维品质,提升逻辑推理和数据分析素养. 有效教学的最高体现是授人以渔——培养学生的探究能力和终身学习能力. 教师以不变的教育初心,实践有效教学,收获递增的育人成就. 如果“春种、夏长、秋收、冬藏”是自然规律,那么高中数学的有效教学播种了最好的种子. 因为数学思维会成为学生永恒的习惯,数学核心素养会化作学生永远的陪伴.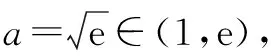
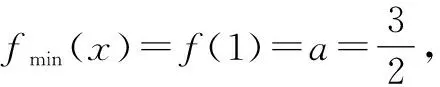
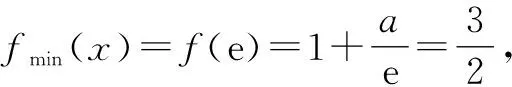
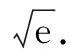
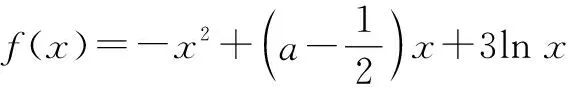
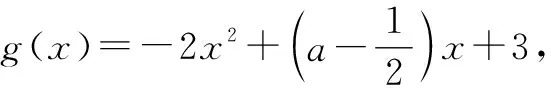
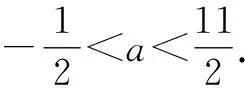
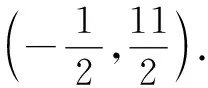
3 结语

