以题促教 以法增效——微专题“让复合函数的零点问题不再烦恼”的教学设计

⦿浙江省宁波市北仑明港高级中学

郭利芳

1 微专题的认识

依托主题明确、针对性极强的“微专题”进行高三复习，可以促进学生深度学习，有利于学生获得清晰的数学知识网络、系统的数学研究方法，加深对数学知识的理解，提高自身的数学素养，也符合新课标中以生为本和可持续发展的教学理念.

2 教学内容背景

零点问题是高考的一个热点问题，而复合函数的零点亦是一个难点.它涉及内外两层函数，问题的解决往往涵盖数形结合、分类讨论、转化化归等数学思想，所以，复合函数的零点问题具有关系复杂、综合性强、难度大等特点，对学生的思维能力、运算能力和分析能力都有较高的要求.本节课的主要教学思路是以方法为主、附以知识的应用和能力的培养，通过例题的稚化、回归、变式、拓展四个维度，在数学思想的渗透中归纳此类问题的常用解题策略，提升教学效果，实现以题促教、以法增效的目的.

3 教学案例设计

环节一：典例展现.

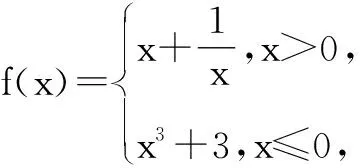
A.3B.4C.5D.6

设计意图：学生此题得分率较低，对他们来说是一个难点，而零点又是高考热点，因此，展开复合函数的零点个数问题的教学，符合学情和考情，即符合微专题的设计理念.

环节二：温故知新.

(1)零点定义：对于函数y=f(x)(x∈D)，把使f(x)=0的实数x叫做函数y=f(x)(x∈D)的零点.

(2)关系：函数y=f(x)有零点⟺方程f(x)=0有实数解⟺函数y=f(x)的图象与x轴有交点.

(3)复合函数y=f(g(x))常见解题策略：由内到外、由外到内，均体现着内层函数的整体性.

设计意图：以问题带动知识的回忆，在知识的回顾过程中整理问题的常用解法，充分调动学生参与课堂的积极性.

环节三：抽丝剥茧.

(1)稚化例题.

已知奇函数f(x)、偶函数g(x)的图象分别如图1、图2所示，若方程f(g(x))=0，g(f(x))=0的实根个数分别为a，b，则a+b=______.

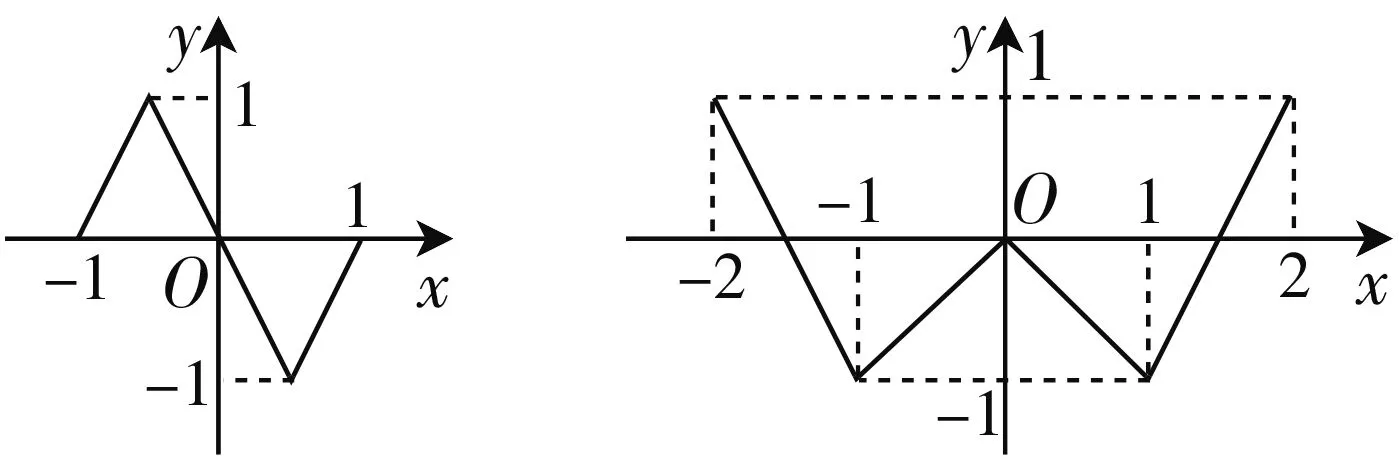
图1 图2

设计意图：先从简单问题出发，一来让学生感受此类问题通过数形结合的方法定性判断零点个数，相比代数法计算出零点值要简单便捷；二来利用此题“以形助数”的方法，促进学生对数形结合的理解；三来促进学生加深理解函数与方程之间的关系.

(2)回归例题.

A.3B.4C.5D.6

解：令2x2+x=t，作出外层函数y=f(t)的图象，定性判断外层函数的零点情况；再作出内层函数，观察内层函数2x2+x=t的图象，定性判断内层函数零点情况.

故选答案：A.

设计意图：在稚化引例的基础上，学生对复合函数的零点问题已有方向，在解决复杂的引例时找回自信，并能根据函数图象自然想到分类讨论标准，进而在数形结合思想的指引下成功解决问题.整个过程较好地培养了学生逻辑推理、直观想象和数学运算等核心素养.

(3)例题变式.

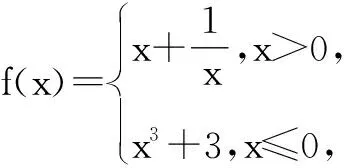
设计意图：通过变式的设计，不仅培养学生的逆向思维，也强化了学生利用数形结合解决复合函数零点问题的方法，较好地提升了学生逻辑推理、直观想象和数学运算等核心素养.

环节四：归纳提炼.

通过对例题的“抽丝剥茧”，引导学生归纳总结求解复合函数y=f(g(x))零点问题的技巧.

设计意图：通过学生合作交流、归纳总结、梳理通法，掌握用数形结合的方法处理复合函数的零点个数问题，加深函数与方程、数形结合、分类讨论与转化化归思想的理解和应用，培养数学抽象的能力.

环节五：直击热点.

(1)设函数f(x)=x2-x-1，若方程f(f(x))=t恰有三个实根，则实数t=______.

(3)已知函数f(x)=|x2-4x+3|，若方程[f(x)]2+bf(x)+c=0恰有7个不相同的实根，则实数b的取值范围是______.

设计意图：巩固知识，理解函数与方程、数形结合、分类讨论、转化化归等数学思想，提升学生综合运用数学知识的能力.

环节六：归纳总结.

研究一个问题——利用图象解决复合函数的零点个数问题；

得出两个步骤——内外兼修；

运用三个数学思想——数形结合、转化化归、分类讨论；

提升四个素养——逻辑推理、直观想象、数学运算、数学抽象.

设计意图：挖掘出本质，提炼出主线，总结出一定的数学思想和方法，以期达到见微知著、以小见大、举一反三和培养学生数学核心素养的目的.

4 教学反思总结

本节课主要通过典型的复合函数零点题目展开，在抽丝剥茧中提炼出解决该类问题的通性通法，提升学生数学核心素养，实现以题促教、以法增效的目的.因此笔者认为，微专题复习教学不应只是简单地对同类型的题目进行堆砌，这样只会增加学生的挫败感，而应挖掘出本质，提炼出主线，总结出数学思想和方法，以期达到见微知著、以小见大、触类旁通和培养学生数学核心素养的目的，让学生在事半功倍中快乐学习数学！