关系映射反演原则在中学数学问题解决中的应用

李艳琴 陈 洁

(西藏自治区拉萨市西藏大学理学院 850000)

随着社会经济的不断发展，数学教育也进行了深入改革.人们逐渐开始意识到，在数学教育教学过程中，教师的任务不仅是教给学生数学的基础知识和基本技能，更重要的是教授数学思维方法.时间一长学生会忘记在学校学到的数学知识和技能，但大脑中留存的一些数学思维方法可能会伴随他们一生，他们仍然可以使用这些数学方法来解决实际问题，这就是所谓的“授人以鱼，不如授人以渔”，真正达到学以致用的目的.在这个过程中，还可以培养学生的逻辑思维能力，提高学生分析和解决问题的能力.由我国著名数学教育家徐利治先生提出的关系(Relationship)映射(Mapping)反演(Inversion)原则(简称RMI原则),作为一种分析和解决问题的思维方法，被广泛应用于数学教育领域.许多数学教育研究者使用这种方法来攻克难以直接解决的数学问题，一些数学老师将这种方法渗透到课堂中，帮助学生理解数学知识、概念等.

迄今为止，关于RMI原则应用的研究主要集中在数与代数领域，更多体现在高等数学中，而在几何领域的具体应用研究相对较少.其实，在中学几何领域许多数学问题解决中也蕴含了此方法.基于此，本文主要讨论RMI原则在中学数学几何部分的具体应用.

1 RMI原则概述

1.1 RMI原则的基本内容

关系(Relationship)映射(Mapping)反演(Inversion)原则(简称RMI原则)是数学教育中应用极其普遍的一种方法.它是将一个不易解决的数学问题转化成一个新问题，这个新问题的解可以很容易地通过某些数学方法或程序得到，当新问题的解被求出后，将新问题的解反演到原问题中，以此得到原问题的解的研究方法.简而言之，RMI原则是一种把问题简单化，让困难问题变得更容易的思维方法.这种方法不仅应用在数学领域，在其他科学领域，也可以看到使用RMI原则来解决问题的现象，因此可以说RMI原则是一种普遍应用于各个领域的科学方法论原则.

关系映射反演原则的基本含义，可以用如下框图表示:

图1

对框图简单地解释说明：在原像关系结构Q中含有原像未知目标x，x是我们不能或不太容易直接求出的量，那么通过可逆映射φ，将需要求的量x映射到映像关系结构Q′中，在Q′中有与原像未知目标x对应的映像x′，如果将x′确定下来，再通过反演也就是逆映射φ-1就能把原像未知目标x确定下来，这样一个求解问题的方法与过程就叫做关系映射反演原则.这里需要注意的是在映射φ中原像目标与映像目标需一一对应，且我们找的映像x′应该是相对较易求得的量.

1.2 RMI原则的具体应用

光看RMI原则，很多人可能不知道是什么意思，只感觉难懂，以为只有研究人员才会用.其实在现实生活中，我们已经有很多使用RMI原则解决实际问题的例子.例如我们使用的温度计，人们无法直接知道人体的体温，于是想到了将体温的测量转换为水银柱膨胀和收缩的测量，通过水银柱膨胀和收缩测得的数值可以反映体温，这种转换使我们可以轻松测量体温，这是RMI原则实际应用的一个简单例子.RMI原则就是将问题映射到另一个不同的论域系统中，在那里获得解决之后再返回来求得本系统问题解决的思维方法.综上所述，RMI原则的基本思想也是一种转化思想.

2 RMI原则在中学数学“空间与图形”领域中的应用

学习数学不仅要学习理论知识，还要学习相应的精神、思想和方法，掌握一些基本的数学思维方法，可以让学生轻松解决数学问题，也可以让学生体验数学之美.在中学数学学习中，结合具体的数学知识，渗透一些数学思维方法，不仅可以帮助学生更好的理解和掌握晦涩难懂的数学概念，还可以让学生体验数学思维的形成过程，培养理性精神，发展数学素养.这些思维方法的最基本原则是将困难的问题转化为已知或比较容易解决的问题，RMI原则便是这样一种能将问题化难为易的重要思维方法.在数学教学过程中，教师应有意识地将这种数学思维方法渗透到各种知识、概念和解决问题中，促进学生对数学学习有更深层次的理解，从而培养学生的数学兴趣和数学思维.

2.1 RMI原则在几何图形初步认识中的应用

中学生对几何图形的初步学习，大多是从认识现实生活中物体的形状开始的.将几何图形映射到现实世界中的物体上，从生活中的各种物体中识别几何图形，了解图形的形状、大小和位置关系，然后反演到数学中，达到认识图形、理解图形的目的，这个过程则体现出了RMI原则的基本思想.

例如，认识球可以映射到现实生活中的特定球体形状，具体映射过程如下：

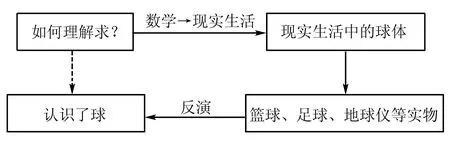
图2

2.2 RMI原则在解立体图形问题中的应用.

在中学阶段，学习几何图形将通过现实世界的物体识别立体或平面图形，在求解几何图形问题时，一般是对平面图形的讨论，但偶尔也会遇到超出我们知识范畴的数学问题，比如一些立体图形问题的求解.而对于一些难以解决的立体图形问题，我们往往会想到将其转化为平面图形进行研究和处理.

例如，人教版七年级上册数学教材中《直线、射线、线段》一章的拓展探究题：

如图3所示，一只蚂蚁想在最短的时间内从正方体的顶点A沿表面爬到顶点B，它应该如何爬行？如果要爬行到顶点C呢？说出你的理由.

图3

解题思路：在本章中，我们学习了“两点之间的最短线段”的概念，对于第一个问题，因为A点和B点在同一平面上，所以学生知道直接连接A点和B点是蚂蚁爬行的最短路径，是到达B点的最短距离.与上一问相比，第二问对于很多学生来说比较困难，因为学生知道A点和C点不在同一个平面上，计算这两点之间的距离是立体几何问题，但是初中阶段学生还没学习解决立体几何两点之间的距离问题，而由于学生学习了立体几何展开图的知识点，有的同学自然会想到用展开图来解题，这样就可以把解立体几何问题转化为求平面图形上的两点之间的距离问题(利用“两点之间，线段最短”的知识，将展开后的图形A和C两点连线就是蚂蚁爬行最短路线，也就是到达C点用时最短的距离)，因此这个问题也可以轻松解决了.

分析可以看出，上述解题思路中有两处体现了RMI原则的思想(1)将时间问题转化为距离问题，找出蚂蚁爬行的最短距离，反演回去得到蚂蚁花费的最短时间；这里简单解释，不深入探讨.(2)解决第二问的关键是建立立体几何问题和平面几何问题之间的映射关系，在平面几何系统中得到解决后，再反演回立体几何问题中,这一解决问题的过程体现了RMI原则.

整个思维过程可用如图4表示：

图4

2.3 RMI原则在解决实际问题模型中的应用

学生在学习数学时,不仅要了解数学知识之间联系，数学与其他学科之间的联系，而且要能够将数学知识与现实生活联系起来，用数学的思维方式去思考，合理地运用所学的数学知识解决实际问题，这是新的课程标准对学生提出的新要求，这一新要求在数学教材后的例题和习题中得到深刻体现.将实际问题转化为数学问题(这个过程就是将实际问题抽象为数学模型)，用特定的数学程序求解数学模型，通过对数学模型的研究得出结论，再反演回实际问题中进行检验，使原问题最终得以解决.这个过程体现了RMI原则的基本思想.

3 小结

本文仅举例说明RMI原则在“空间与图形”领域数学问题解决中的一些应用，笔者认为，上述例子蕴含了RMI原则的基本思想.RMI原则实际上可以理解为是一种科学的方法论原则，广泛适用于各种场景，但RMI原则的应用也需要一定的条件.例如，RMI方法能否成功实现的关键在于其映射和反演是否可行，新问题是否容易解决.

笔者认为，在数学教学中教师若能在数学知识之间以及数学问题解决的过程中提炼出RMI原则，从更高的层次进行教学，将这一基本思维方法渗透给学生，并鼓励学生举一反三应用此原则来解决数学问题和实际问题，这对学生学习数学知识和理解数学问题有很大的帮助，也可以锻炼学生的数学思维能力.