基于温度分析的抽水储能发电机故障模式识别

路 建，李 勇，王宗收，郝崇清

(1.河北张河湾蓄能发电有限责任公司，河北石家庄 050300；2.河北科技大学电气工程学院，河北石家庄 050018)

主站发电机是抽水蓄能发电站核心运行单元，然而发电机组设备在长期运行时存在下导瓦间隙偏小、冷却器容量不足、透平油老化、杂质混入等风险隐患[1]。对一些长期缓慢变化的趋势信息，如发电机瓦温等，采用机器学习算法和大数据处理方法对生成的报表数据进行分析，进而实现故障监测和潜在风险预警，对提高整个系统的稳定性和可靠性，以及给监控系统国产化改造提供了很好的范本，具有很好的推广意义。

基于机器学习的故障监测方法，目的在于通过不同故障模态下信号传感器采集的数据信息，训练学习得到一个数据与故障之间的数学模型，并通过该模型对后测数据进行实时监测，以确定故障类型和时间，其中随机森林、决策树、神经网络、支持向量机等方法已越来越多地应用到各类故障检测和诊断领域[2-5]。李兵等[6]利用一种改进的随机森林算法，在考虑漏报率的基础上提出了电机轴承故障诊断决策方法；郑日晖等[7]提出了优化决策树的智能诊断方法，在简化模型的基础上使得故障分类的准确率大大提升；贾京龙等[8]基于油中溶解气体浓度信息，利用卷积神经网络的方法实现了电力变压器故障诊断。陈如清等[9]基于振动传感器的频谱信息，提出了一种基于递归神经网络的方法，成功用于旋转机械装置的故障诊断。支持向量机作为一种有监督的机器学习方法，其在样本数量、待识别的模式数量以及非线性问题分类等方面均能达到良好效果。樊浩等[10]提出了主元分析结合支持向量机的断路器故障诊断方法，在噪声背景下实现了断路器7种故障的准确分类。然而，支持向量机的惩罚因子以及核函数参数组合较大程度地影响了故障识别准确率，有学者利用各类寻优算法对支持向量机的参数组合进行优化配置以期望获得更高的故障识别准确率[11-13]。近年来，麻雀搜索算法受到了学者们的广泛关注，其可以有效避免陷入局部寻优的问题，现已被成功应用于三维无人机航迹规划[14]。

基于以上分析，提出一种通过主站发电机瓦温信息构建发电机故障诊断模型的方法，利用麻雀算法全局寻优和局部寻优自由切换的优势，对支持向量机的惩罚因子以及核函数参数组合进行优化，以提高发电机故障模式识别准确率。

1 支持向量机分类方法

支持向量机(SVM)是一种具有较强泛化能力、适用小样本学习的模型，被广泛应用于分类和回归等问题。对于线性可分问题，SVM通过建立一个最优决策超平面，满足平面两侧待分类的样本之间距离最大化，从而获得良好的泛化能力和分类效果。对于非线性可分问题，是将低维不易区分的特征点通过核函数实现到高维特征空间的非线性映射，然后在特征空间中建立最优超平面进行分类。

1)设最优决策超平面：

ωφ(x)+b=0，

(1)

式中：ω为权重；b为偏置量。

2)通过ωφ(x)+b>0或ωφ(x)+b<0对x进行分类，决策函数如下：

f(x)=sgn(ωφ(x)+b)。

(2)

3)为了解决非线性可分问题，通过将惩罚因子C和松弛系数ζi引入到目标函数中，以此来间接增大目标函数值。目标函数和约束条件构造如下：

(3)

式中：C为惩罚因子，用于调整样本间的权重；ζi为松弛系数，对应于非线性样本。

4)利用拉格朗日函数及拉格朗日乘子αi解出不等式约束条件下的最大值。

(4)

可得最优分类函数为

(5)

式中：K(x,xi)为支持向量机的核函数；m为向量样本个数。

SVM的核函数种类包括高斯径向基核函数、线性核函数和多项式核函数等。其中，相较于其他核函数，高斯径向基核函数有更好的分类效果，因此采用RBF核函数求解，表达式[15]如式(6)所示：

(6)

2 基于麻雀搜索算法的SVM参数优化

使用虚拟麻雀进行食物的寻找，由n只麻雀组成的种群可如式(7)表示：

(7)

式中：d为待优化问题变量的维数；n为麻雀的数量。则所有麻雀的适应度值可以表示为

(8)

式中f表示适应度值。

在第t次迭代中，拥有较好适应度的第i个麻雀在第j维更新位置为

(9)

式中：itermax为最大迭代次数；α为介于0～1的随机值；Q为服从正态分布的随机值。R2(R2∈[0,1]) 和 ST(ST∈[0.5,1])分别表示预警值和安全值。L表示一个1×d大小的元素为1的矩阵。

在觅食过程中，新入麻雀的位置更新表示为

(10)

式中：Xp是目前发现者所占据的最优位置；Xworst则表示当前全局最差的位置；A表示每个元素随机为±1的1×d向量。

“意识到危险”位置的麻雀位置更新为

(11)

式中：Xbest是当前的全局最优位置；β作为步长控制参数；K∈[-1,1]是一个随机数，表示麻雀移动的方向；fi是当前麻雀个体的适应度值。

由式(3)和式(6)可知，SVM的惩罚因子C和核函数半径g是影响其分类能力的主要因素，其中惩罚因子C可以影响SVM对样本学习的准确性，参数g影响样本的空间投射[16]。通过麻雀搜索算法寻找到最佳的2个参数C和g，进而提高SVM在故障模式识别中的正确率。利用麻雀搜索算法来进行SVM参数优化的步骤如下：

Step1 确定训练样本和测试样本；

Step2 设置麻雀种群规模pop，搜索空间维度dim，最大迭代次数Max_iteration。生成麻雀初始位置，取[-1,1]之间的随机数作为麻雀的初始位置，设置“意识到危险”的麻雀及“发现者”麻雀占比，并确定预警值ST；

Step3 计算出麻雀种群适应度值，得到最优位置Xp和最劣位置Xworst；

Step4 根据式(9)—式(11)更新“发现者”“加入者”“意识到危险”的麻雀位置；

Step5 计算麻雀更新位置后的适应度值，并与前一次迭代中的适应度值做对比。假如高于原有适应度值，则把新位置值作为最优的适应度值Xbest；否则保持原适应度值不变；

Step6 判断是否已经达到了最大迭代次数，若未达到，则转到Step3，若已经达到，则停止迭代过程；

Step7 结束寻优过程，输出最优(C,g)组合，以最优参数构造SVM分类器。

3 实验结果分析

利用张河湾抽水蓄能电站监控系统采集的水泵发电机实测温度数据进行方法的验证和分析。数据覆盖正常、下导瓦间隙偏小、冷却器容量不足、透平油老化、杂质混入故障5种状态模式。每个状态中选取了200组故障样本数据作为研究数据，其中训练样本集160组(占80%)和测试样本40组(占20%)，对故障状态进行诊断测试。限于篇幅，各故障状态下部分温度数据(截取了下导轴承20个温度数据点)变化情况如图1所示，其中相邻数据点之间的采样时间间隔为10 min。

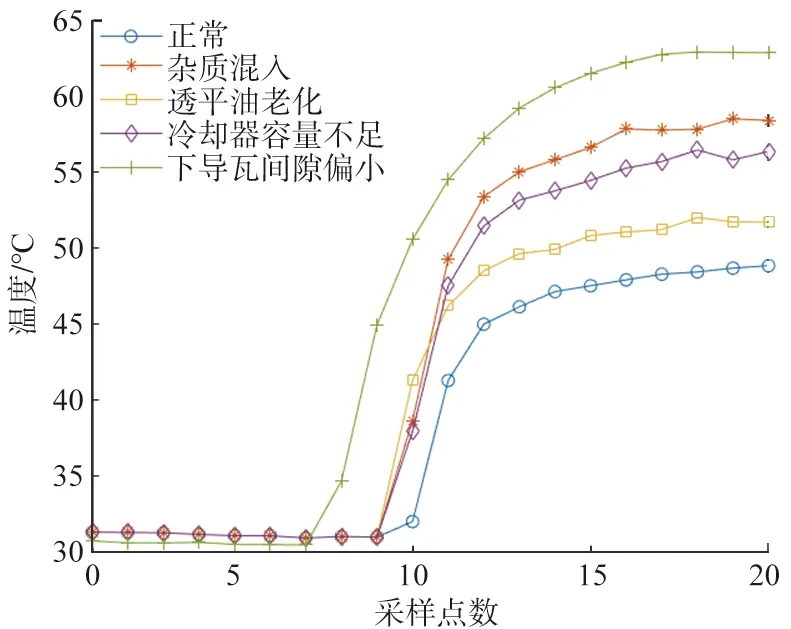
图1 原始温度数据在4种故障模式下的变化情况Fig.1 Distribution of original temperature data in four fault modes

采用本文所提方法对SVM模型进行优化，并完成故障模式识别，其相关参数设置如下：种群规模为50，最大迭代次数为100，搜索空间维度为2，“意识到危险”的麻雀占比为25%，“发现者”麻雀占比为75%，预警值为0.6；SVM模型中惩罚因子C∈[0.01,1]，核函数半径g∈[2×10-5,2×105]。

以识别错误率作为适应度，利用麻雀寻优算法对惩罚因子C和核函数半径g的参数组合寻优，其适应度及参数变化过程分别如图2和图3所示。

图2 麻雀寻优算法的适应度变化曲线Fig.2 Fitness curve of sparrow optimization

图3 惩罚因子和核函数半径的寻优过程Fig.3 Optimization process of penalty factor and kernel radius

由图2可知，麻雀寻优算法在第6次迭代完成了参数寻优，因此，本文所提的麻雀寻优-支持向量机故障识别模型具备较快的收敛速度。参数寻优结果为C=448.5，g=0.036 72，并以此模型对200组测试样本(正常、下导瓦间隙偏小、冷却器容量不足、透平油老化、杂质混入各40组)故障识别测试。其中组数1～40为正常测试样本，组数41～80为下导瓦间隙偏小故障测试样本，组数81～120为冷却器容量不足故障测试样本，组数121～160为透平油老化故障测试样本，组数161～200为杂质混入故障测试样本。模型对测试样本的识别结果及识别正确率统计分别如图4和表1所示。为了验证本文所提方法在提升识别正确率方面的有效性，传统SVM模型识别的统计结果如表2所示。

由表1的统计分析可知，正常和冷却器容量不足故障测试样本的正确率最高，均可达到95%，下导瓦间隙偏小故障测试样本的正确率较低为87.5%。在200个测试样本中，识别错误的样本数为16，其总体识别正确率达到92%。由表1和表2的数据对比，可见本文所提方法将200组测试样本的识别正确率提高了7%。然而，下导瓦间隙偏小故障的识别错误样本数仍然偏高。

图4 测试样本识别结果Fig.4 Identification results of the test samples

此外，为验证所使用的麻雀寻优-支持向量机(Sparrow-SVM)方法较现行主流故障模式识别方法的优势，分别利用粒子群-支持向量机(PSO-SVM)、遗传算法-支持向量机(GA-SVM)和麻雀寻

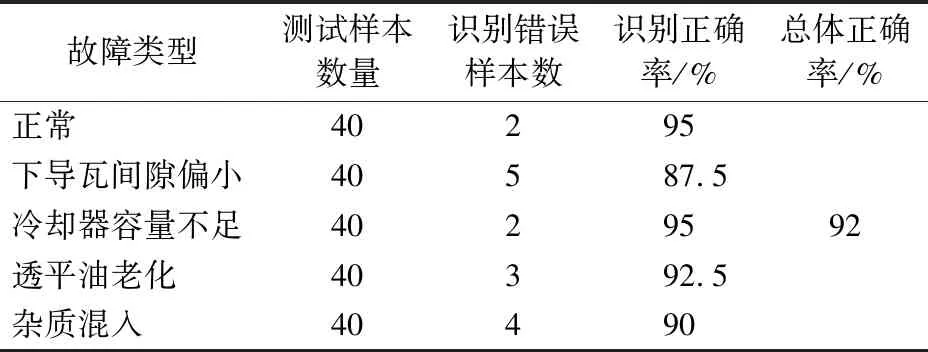
表1 基于麻雀寻优-支持向量机方法的测试样本识别正确率统计Tab.1 Statistical results for the identification accuracy of the test samples based on Sparrow-SVM

表2 基于传统SVM的测试样本识别正确率统计Tab.2 Statistical results for the identification accuracy of the test samples based on traditional SVM

优-极限学习机(Sparrow-ELM)以相同数据样本进行训练并测试识别，相应的统计结果如表3所示。由数据分析可知，Sparrow-SVM方法识别正确率均高于被对比的其他3种主流方法。一方面验证了麻雀寻优方法较传统粒子群寻优、遗传算法寻优的优势；另一方面说明在抽水蓄能电站主机故障训练样本有限的情况下，SVM方法较ELM方法故障模式分类效果更佳。

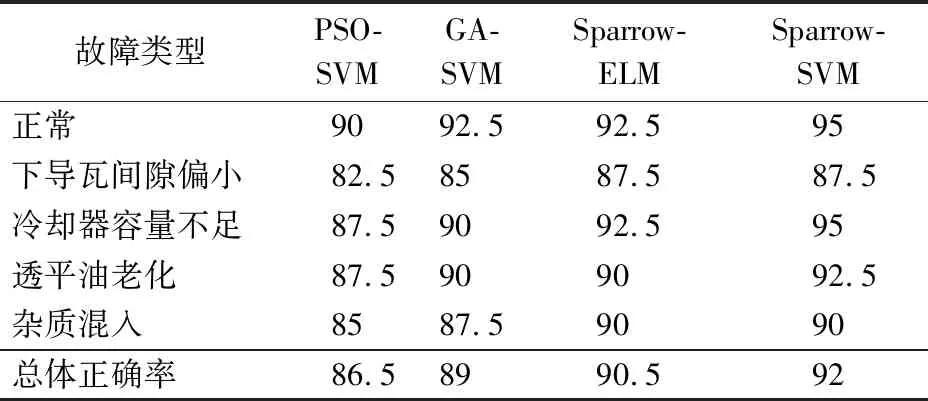
表3 与现行同类方法识别结果对比Tab.3 Performance comparison with other current fault pattern recognition methods 单位：%

4 结 语

提出了一种基于温度信号分析的麻雀寻优-支持向量机发电机故障模式识别方法，经数据分析得到相关结论如下。

1)抽水蓄能电站下导瓦间隙偏小、冷却器容量不足、透平油老化、杂质混入故障可导致发电机瓦温等信息的变化。

2)通过瓦温构建的故障样本可用于训练SVM模型并可实现实测数据的故障类型识别，同时，麻雀寻优算法可快速有效地对SVM的惩罚因子C和核函数半径g进行寻优。与传统SVM识别方法相比，麻雀寻优-支持向量机可将样本识别正确率从85%提升至92%，在200组测试样本中，识别错误样本数由30组降至16组。

3)张河湾抽水蓄能电站故障下实测温度数据表明，本文所提出的麻雀寻优-支持向量机方法可进行故障模式识别，为机组运行状态的智能化监测提供了有效支撑，为抽水蓄能发电站主站电机的安全可靠运行提供了技术保障。

采样过程中温度波动对温度变化率的影响容易导致下导瓦间隙偏小故障发生误判。基于以上分析，各类故障下温度数据的预处理将作为今后研究的重点。