基于SA-CS算法的分布式电源接入配电网规划研究

何自争，邱 怡，陈逸馨，朱 洁，刘 闯

(1.国网湖北省电力有限公司 襄阳供电公司，湖北 襄阳 441000； 2.国网湖北省电力有限公司 荆门供电公司，湖北 荆门 448000)

0 引 言

随着“碳达峰”和“碳中和”目标的提出，国家越来越重视节能减排[1-2]。近年来，配电网中接入的光伏、风电等分布式电源(distributed generation，DG)的容量越来越大，这在一定程度上减少了化石能源的使用量，降低了碳排放，但分布式能源的接入会改变配电网的潮流分布，另外由于光伏、风电等分布式电源具有较大的波动性，并网后会对系统稳定性和电能质量产生不良影响[3]。因此，对分布式电源接入配电网规划进行研究具有重要意义。

为了获得更合理的DG接入配电网规划方案，国内外专家学者进行了大量研究。文献[4]采用多种群遗传算法对分布式光伏接入配电网规划进行了研究，提出了一种兼顾安全性和经济性的光伏并网规划方案。文献[5]以配电网中各分布式电源的年综合费用最小为目标函数，综合考虑各类约束，建立了基于双层粒子群算法的主动配电网分布式电源规划，并用实际算例验证了模型的实用性。文献[6]为了降低分布式电源接入配电网带来的不利影响，利用仿射数模型降低了分布式电源出力预测的不确定性，提出了一种考虑多类型负荷及风光不确定性的配电网优化规划模型，并利用自适应遗传算法对模型进行了求解，取得了不错的应用效果。配电网中DG优化规划是一个包含多变量和多约束的非线性问题，采用遗传和粒子群等常规优化算法容易陷入局部最优，因此如何提高规划模型的求解精度是目前亟待解决的关键问题之一。

针对现有配电网中DG优化规划方法中存在的不足，本文综合考虑含分布式电源的配电网运行过程中的各项成本和约束条件，建立以配电网总投资成本最小为目标函数的分布式电源接入配电网规划模型，采用引入模拟退火机制的布谷鸟算法对模型进行求解，并采用实际算例验证本文提出的配电网规划模型及求解方法的正确性和优越性。

1 分布式电源接入配电网规划模型

1.1 目标函数

配电网总投资成本主要包括建设成本、维护成本、有功损耗成本和各类惩罚成本[7]，该文以配电网总投资成本为目标函数，具体如下：

minF=FDG+FPloss+FU+Fl+Ff

(1)

式中：FDG为折算到每年配电网中分布式电源的建设、维护成本；FPloss为配电网总有功损耗成本；FU为配电网节点电压越限后的惩罚成本；Fl为配电网支路电流越限后的惩罚成本；Ff为配电网中DG总容量越限后的惩罚成本。

1.1.1 折算到每年DG的建设、维护成本

折算到每年配电网中分布式电源的建设、维护成本可以根据设备折现率来进行计算，其计算式如下：

(2)

(3)

式中：δ为配电网中分布式电源的固定年均投资成本系数，CDG，i、CW，i分别为第i个分布式电源的单位电量的建设投资成本和维护成本；Pi为第i个分布式电源的输出功率；r为年利率；t为规划时间。

1.1.2 配电网总有功损耗成本

配电网总有功损耗成本主要来源于线路阻抗，其计算式为

(4)

式中：Ce为单位电价；Tmax为年最大负荷损耗小时数；Ploss为配电网中第m条支路的有功损耗；b为配电网支路总数。

1.1.3 节点电压越限后的惩罚成本

节点电压越限后的惩罚成本是指配电网中分布式电源接入不合理时造成配电网节点电压越限带来的惩罚成本，其计算式为

(5)

fU，i=(max(0,|Ui，min-|Ui|)+

max(0,|Ui|-|Ui，max|))

(6)

式中：KU为配电网节点电压越限后的惩罚系数；Ui为第i个节点的节点电压；Ui，min、Ui，max分别为第i个节点的节点电压下限和上限；n为配电网节点总数。

1.1.4 支路电流越限后的惩罚成本

支路电流越限后的惩罚成本是指配电网中分布式电源接入不合理时造成配电网支路电流越限带来的惩罚成本，其计算式为

(7)

fl，m=(max(0,|Im|- |Im，max|))2

(8)

式中：Kl为配电网支路电流越限后的惩罚系数；Im为第m条支路的电流；Im，max为第m条支路的电流的上限。

1.1.5 DG总容量越限后的惩罚成本

配电网中接入DG的容量是有限的，容量会带来相应的惩罚成本，其计算式为

Ff=KDGfDG

(9)

fDG=(max(0,|SDG|-|Ssup|))2

(10)

式中：KDG为配电网中DG总容量越限后的惩罚系数；SDG为配电网实际接入DG总容量；Ssup为配电网允许接入DG总容量的上限。

1.2 约束条件

1)功率平衡约束

(11)

式中：PDG,i、QDG,i分别为DG注入节点i的有功功率和无功功率；PL,i、QL,i分别为线路注入节点i的有功功率和无功功率；Ui、Uj分别为节点i和节点j的电压；Gij、Bij、θij分别为节点i和节点j之间的电导、电纳和相角差。

2)节点电压约束

Ui，min≤Ui≤Ui，max

(12)

3)支路电流约束

Im≤Im，max

(13)

4)DG总容量约束

SDG≤Ssup

(14)

5)各节点DG接入容量约束

SDG,i≤Si,max

(15)

式中:SDG,i、Si,max为分别为节点i的DG实际接入容量和最大允许接入容量。

2 引入模拟退火机制的布谷鸟算法

2.1 布谷鸟搜索算法

布谷鸟搜索(cuckoo search，CS)算法是根据布谷鸟寄生繁殖行为提出的一种新型智能优化算法，其迭代遵循莱维飞行机制， CS算法的寻找原理可参考文献[8]。CS算法原理简单、操作方便、容易实现，但CS算法的搜索步长和搜索方向存在较大偶然性，算法在寻优过程中容易出现早熟现象，陷入局部最优。

2.2 模拟退火算法

模拟退火(simulated annealing，SA)算法是基于热力学经典粒子系统降温过程得到的一种优化算法。孤立粒子系统温度下降速度很慢时，其内部热量近似处于平衡状态，最终释放热量至最低状态，即能量函数最小值[9]。SA算法中控制参数T的取值均满足Metropolis准则，在迭代时不断进行“产生新解—判断—接受或放弃”的操作，使系统达到平衡状态，即找到最优解。

2.3 SA-CS算法

为了提高CS算法的搜索精度，在CS算法中引入模拟退火算法的寻优策略，形成模拟退火-布谷鸟混合算法，简称SA-CS算法。在算法寻优过程中，一旦陷入局部最优解时，鸟巢位置更新不再进行下一次迭代，而是采用模拟退火机制对其中一部分鸟巢进行位置更新，从而生成位置更好的鸟巢进行迭代计算，以避免算法在寻优过程中陷入局部最优。

SA-CS算法实施的关键在于判断合适的退火时机，即当算法陷入局部最优时，采用模拟退火机制对其中一部分鸟巢进行位置更新。本文根据最优鸟巢位置的适应度值变化率进行判断，求取为当前代数最优鸟巢位置适应度值和前m代最优鸟巢位置的适应度值差值的绝对值与当前代数最优鸟巢位置适应度值的比值，具体公式如下：

(16)

设定适应度值变化率阈值为0.005，即当α<0.005时采用模拟退火机制对其中一部分鸟巢进行位置更新。研究表明，SA-CS算法既能发挥布谷鸟算法良好的寻优能力，又能利用模拟退火机制使算法避免陷入局部最优，提高搜索效率。

3 SA-CS算法求解DG接入的配电网规划模型

采用SA-CS算法对DG接入配电网规划模型进行求解，确定DG接入点和接入容量，在满足各类约束的同时使配电网总投资成本最小，具体步骤如图1给出的模型的求解流程。

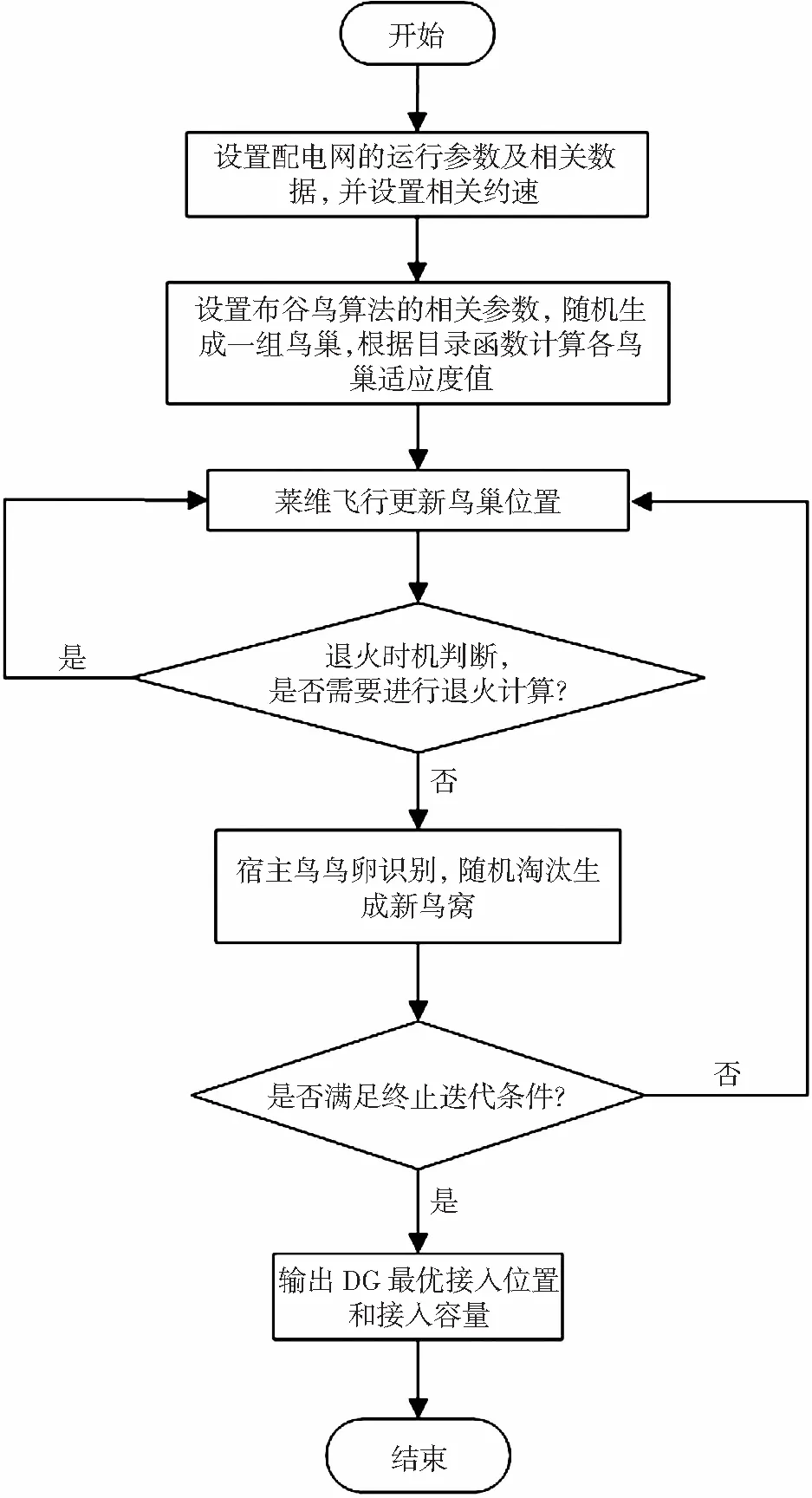
图1 模型求解流程

1)设置配电网的运行参数及相关数据，并设置相关约束。

2)设置SA-CS算法的相关参数，包括种群规模，最大迭代次数，布谷鸟的鸟卵被发现概率和步长因子等。

3)随机生成一组鸟巢，并对每个鸟巢的适应度值进行计算，将适应度值最好的鸟巢位置进行保存。

4)利用莱维飞行公式更新鸟巢位置，获得一组新鸟巢，对新鸟巢的适应度值进行计算，并将其与最优适应度值进行比较，如果更好则将其更新为最优适应度值，否则保持不变。

5)判断算法是否陷入局部最优，若小于设定阈值，则采用模拟退火算法对其中一部分鸟巢进行位置更新，并将剩余一部分鸟巢两两相交，然后将两部分合并组成新的鸟巢，计算合并后鸟巢的个体适应度值，保存最优适应度值，然后返回步骤3。否则，转到下一步。

6)随机生成一个数r，将随机数r与布谷鸟的鸟卵被发现概率pa进行比较，若果r>pa，则随机变化当前鸟巢位置，得到新一代鸟巢位置，计算鸟巢的个体适应度值，保存最优适应度值。

7)判断算法是否达到最大迭代次数，若是则输出DG最优接入位置和接入容量，否则返回步骤3继续迭代。

4 算例分析

以IEEE33节点配电网系统进行算例分析，其网络结构如图2所示。该系统基准容量和额定电压分别为10 MVA和12.66 kV，系统总有功功率和无功功率分别为3 715 kW和2 300 kvar，系统网损为203 kW。在IEEE33节点配电网系统中，0节点为源节点，不允许接入DG，其余32个节点均可接入，但每个节点只允许接入1台DG，其基准容量为50 kVA，最大容量为200 kVA。待接入的DG均按PQ节点处理，功率因素取0.9，每台DG单位电量的基准投资成本CDG和维护成本CW分别为1 200元/kW和50元/kW，且正比于DG接入容量，单位电价Ce为0.5元/kW·h，年最大负荷损耗小时数为3 000 h，DG最大接入总容量不大于系统总容量的10%，电压偏差取±7%。

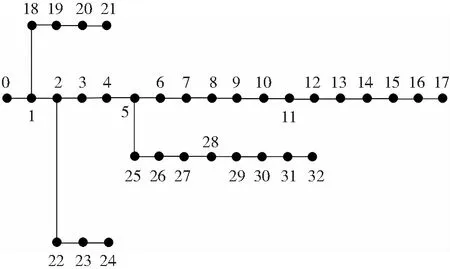
图2 IEEE33节点配电网系统

SA-CS算法的相关参数设置如下：种群规模N=100，最大迭代次数kmax=200，布谷鸟的卵被发现概率Pa=0.25，控制参数初值T0=3，终值Tend=0.01，马尔科夫链长度L=30，衰减系数A=0.9。

在Matlab中建立仿真模型，应用SA-CS算法对IEEE33节点配电系统中DG接入位置及容量进行规划，规划结果如表1所示。由表1可知，DG接入位置分别为节点14、25、29、31和32，总接入容量为300 kVA，满足要求。

表1 DG接入位置及容量

各节点电压在DG接入后的变化情况如图3所示。由图3可知，DG接入后，除源节点外，其余节点电压均有改善，DG接入前的最低电压为0.913(p.u.)，接入后的最低电压为0.947(p.u.)，满足电压质量要求。

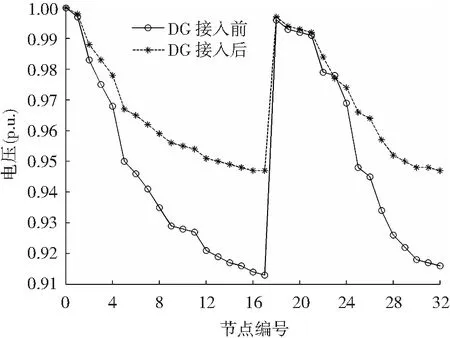
图3 DG接入前后各节点电压变化情况

图4给出了SA-CS算法寻找目标函数最优值的迭代过程，SA-CS算法经过49次迭代后找到了最优解，即总投资成本Fmin=26.541万元。

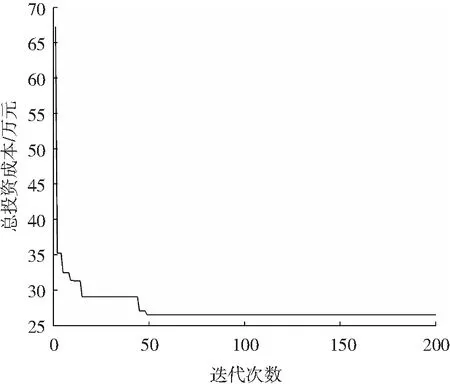
图4 SA-CS算法迭代寻优曲线

为了进一步验证SA-CS算法在DG接入配电网规划方面的优越性，采用CS算法和PSO算法对目标函数进行求解，CS算法和PSO算法的参数设置可参考文献[10-11]，3种算法的寻优结果如表2所示。由表2可知，SA-CS算法找到最优解的迭代次数和收敛时间远小于CS算法和PSO算法，而SA-CS算法的求解精度高于其他2种优化算法，由此可见引入模拟退火机制的布谷鸟算法能够有效减少迭代次数，提高计算精度。

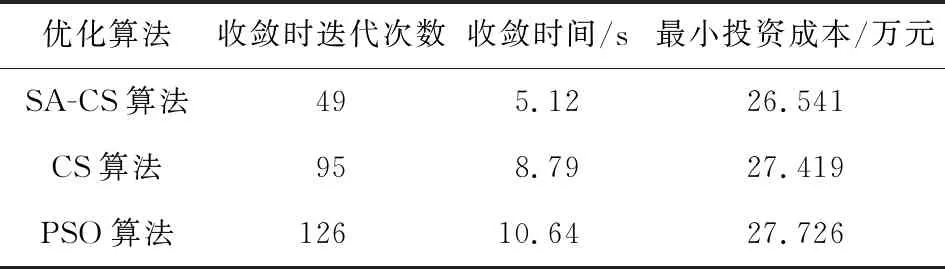
表2 3种算法寻优结果对比

5 结 语

综合考虑含分布式电源的配电网运行过程中的各项成本和约束条件，建立以配电网总投资成本最小为目标函数的分布式电源接入配电网规划模型。在布谷鸟搜索算法中引入模拟退火机制，避免算法在寻优过程中陷入局部最优，提高算法的搜索效率。以IEEE33节点配电网系统为例进行算例分析，采用引入模拟退火机制的布谷鸟算法对模型进行求解，并与其他优化算法的求解结果进行对比，结果表明，SA-CS算法在收敛时间和求解精度方面均优于其他算法，验证了所提配电网规划模型及求解方法的正确性和优越性。