基于移动主成分分析与集成学习的结构损伤识别方法

周 颖，刘泽佳，张 舸，周立成，刘逸平，汤立群，蒋震宇，杨 宝

(1. 华南理工大学 土木与交通学院，广东 广州 510641；2. 广东省建筑科学研究院集团股份有限公司，广东 广州 510599)

20世纪中叶以来，科学技术的快速发展推动了桥梁工程技术的飞跃。随着桥梁建设规模的扩大，造价越来越高，大型桥梁在国民经济和社会生活中的作用越来越重要，人们对大型桥梁的安全性、耐久性与正常使用功能日渐关注[1]。桥梁在服役过程中不可避免地发生各种结构损伤，损伤的原因可能是使用不当、维护不当、车祸事故等人为因素，也可能是自然灾害。为了避免损伤引起结构失效而造成事故，大型桥梁在建造过程中会安装结构健康监测(structural health monitoring,SHM)系统。SHM系统通过现场布置的传感器系统返回大量监测数据，为开展SHM基础科学研究奠定了基础[2]。

在桥梁SHM应用中，SHM系统现场传感器所采集的监测数据中不可避免地包含大量的环境噪声。这些噪声会大幅降低损伤监测的效率和可靠性，因此有必要对SHM数据进行特征分析，去除噪声影响，同时放大结构损伤对数据变化的影响。

主成分分析(principal component analysis,PCA)是SHM领域中使用广泛的一种特征分析方法。PCA可通过协方差矩阵计算过滤掉原始高维特征空间数据中的结构噪声和冗余，转化为低维空间中具有可解释性的数据，在排除混淆数据的同时能保留主要信息。已有研究[3]验证了使用PCA基于长期健康监测的振动信号对结构损伤进行识别的可行性，但是PCA无法满足SHM工作中的实时监测要求，为此Posenato等[4]提出移动主成分分析(moving principal component analysis,MPCA)。该方法在PCA的基础上增加一个移动时间窗口，引入时间维度方向结构安全状态的变化，从而实现了结构的实时监测。

MPCA将信号的时间序列分解为特征值时间序列和特征向量时间序列。将特征向量作为结构固有属性特征的表征，则特征向量在时间维度上的变化可反映结构的健康状态。文献[5]中应用MPCA对结构损伤的发生和位置进行识别，发现MPCA可以在早期识别到结构损伤造成的响应变化。文献[6]中对比了MPCA和稳健回归分析2种特征分析方法，发现MPCA能识别损伤程度和长度更小的损伤。文献[7]中验证了MPCA与机器学习相结合的结构损伤识别方法具有较好的检测性能和抗噪性能。由此可知，MPCA对于结构健康实时监测具有很好的潜力，与人工智能相结合可以实现智能结构损伤识别。

PCA的计算过程是通过数据在不同方向的离散度排序，得到第一特征向量、第二特征向量……。由于第一特征向量中包含原始数据中绝大部分信息，已有研究[5-9]中大多只探讨以第一特征向量作为损伤指标对损伤发生、损伤定量和损伤定位进行分析，而忽略了高阶特征向量的作用。文献[10]中通过对MPCA的第二特征向量进行分析，发现该指标的演变可用于指示结构在损伤发生后是否达到新的稳定状态。由此可知，在结构损伤识别过程中，如果考虑高阶特征向量，则可获得更多损伤关联信息，然而结合多个特征向量提高结构损伤识别效果的研究亟待开展。

本文中提出结合MPCA第一、第二特征向量的组合特征向量作为损伤指标的损伤识别方法。将MPCA计算双跨平面梁模型的监测数据所得的组合特征向量与第一、第二特征向量分别作为损伤指标输入决策树(decision tree,DT)，损伤长度或损伤位置作为DT的输出，分别进行损伤定量和损伤定位，在准确性、鲁棒性方面对3种损伤指标进行比较，分析组合特征向量相对于单个特征向量的优势，并采用集成学习模型与组合特征向量相结合，进一步改善损伤识别性能。

1 结构损伤识别方法

1.1 识别方案

结构损伤识别方法步骤如下：

步骤1 基于数据采集和无线技术，利用安装在结构上的传感器获取结构的实时监测数据。

步骤2 确定时间窗口长度，利用MPCA对监测数据进行计算，得到第一、第二特征向量的时间序列数据，对比损伤敏感度，进而确定损伤指标。

步骤3 以损伤指标作为集成学习模型的输入，损伤长度或损伤位置作为输出，分别进行损伤定量和损伤定位。

1.2 特征提取方法

1.2.1 PCA

在SHM领域，PCA主要用于对数据进行降维，在去除冗余信息的同时，保留原始数据中的有效信息。本文中PCA用于增大不同损伤工况时结构特征之间的差异。根据应变响应数据协方差矩阵的特征向量对结构行为进行分析，可以很好地表征损伤发生、损伤程度和损伤位置。

假设原始应变响应数据矩阵为

(1)

式中：Xij为不同时间点不同传感器位置处的应变响应数据，i=1,2,…,T,j=1,2,…,N；T为采集数据的时间点个数；N为数据中特征的个数，即传感器个数。

步骤1 去均值。计算每个特征的平均值，然后对于所有样本，每个特征都减去自身的均值，即

(2)

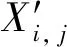
步骤2 令X′=(Y1,Y2,…,YN)，计算协方差矩阵

(3)

其中X′的分量Yi、Yj(i,j=1,2,…,N)的协方差ci,j为

ci,j=Cov(Yi,Yj)=E[Yi-E(Yi)][Yj-E(Yj)],

(4)

式中E(·)为随机变量的数学期望。

步骤3 计算协方差矩阵的特征值和对应的特征向量。

通过特征值分解，可求得协方差矩阵C的特征值λi和对应的特征向量Ψi，

CΨi=λiΨi,i=1,2,…,N。

(5)

将特征值按从大到小的顺序排序，最大特征值对应的特征向量为第一特征向量，其次为第二特征向量，以此类推。

1.2.2 MPCA

由于SHM在工作中会产生海量数据，为了提高数据处理的效率，MPCA首先利用时间窗口对数据进行划分，再利用PCA对时间窗口数据进行特征提取，第i个时间窗口数据矩阵为

(6)

式中l为时间窗口长度。

对Xi进行PCA计算，可以得到该窗口数据的第一、第二特征向量等。随着时间窗口的前移，可以得到特征向量的时间序列数据，用于结构的实时监测。MPCA有移动窗口，相对于PCA，每一步的计算成本较低，对异常数据的识别也更及时，原因是旧的测量数据不会对识别结果产生影响。由于应设定窗口足够大，以显现周期性变化，因此理论上窗口大小应为数据变化周期的数倍。本文中数值模拟时数据变化的周期性体现在温度随季节的变化，因此选择1 a的窗口大小，从而使计算成本较低。

1.3 分类模型

结合MPCA与人工智能算法构建结构损伤识别方法，对比MPCA与DT、k近邻学习(k-nearest neighbor,KNN)、随机森林(random forest,RF)、极限梯度提升(extreme gradient boosting,XGBoost)4种典型机器学习分类模型的适应性，其中RF和XGBoost属于集成学习模型。

1.3.1 DT

DT是一种类似于流程图的树形结构，表示对象属性与对象值之间的映射关系，是由节点和边2种元素组成的结构，节点又分为根节点、父节点、子节点和叶子节点。子节点由父节点根据某规则分裂而来，然后子节点作为新的父节点继续分裂，直至不能分裂为止；根节点是没有父节点的节点，即初始分裂节点；叶子节点是没有子节点的节点。DT的每个节点为对一个特征的测试，树的分支为该特征的每个测试结果，而树的每个叶子节点为一个类别。

1.3.2 KNN

KNN算法的实现原理[11]如下：给定一个训练数据集，将新的未知样本输入分类模型后，计算未知样本与所有训练数据集中已知样本的距离，选取与未知样本距离最近的k个已知样本，根据少数服从多数的投票法则，将未知样本与k个最邻近样本中所属类别占比较多的归为一类。KNN模型实际上就是对特征空间的划分。

通常使用的距离函数有欧氏距离、余弦距离、汉明距离、曼哈顿距离等。本文中数据为传感器数值，因此采用欧氏距离。h维空间中点(x1,x2,…,xh)与点(z1,z2,…,zh)的欧氏距离为

(7)

1.3.3 RF

在Breiman[12]于2001年提出RF后，不同学者对RF进行完善，引入了随机节点优化和装袋(bagging)集成学习思想。利用装袋集成学习思想，RF将多棵树进行集成。该算法的基本单元是DT。

由于RF在DT的构建过程中增加了随机性，因此每棵DT的构建过程都与其他DT的构建过程略有不同。DT的生成有2个随机性，即数据点随机性、特征随机性，因此可以在保证所有DT预测能力的同时减少单个DT的过拟合。

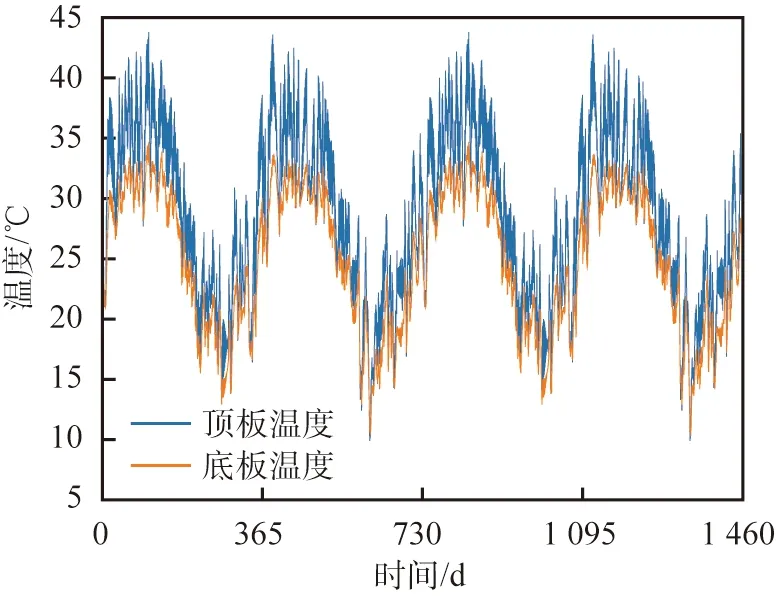
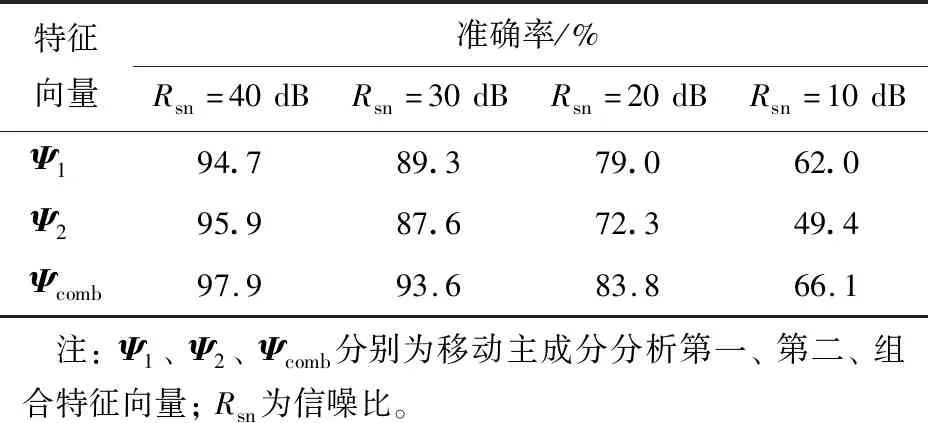
RF中DT的生成规则如下：假设训练集中样本总个数为S，随机且有放回地从训练集中提取s个样本作为DT的训练集；假设特征维度为D，指定常数d

1.3.4 XGBoost

Boosting是一簇可将弱学习器提升为强学习器的算法。工作机制如下：先从初始训练集中训练出一个基学习器，根据基学习器的表现对训练样本权重进行调整，使得基学习器学习误差率高的训练样本能在后续受到更多重视，然后基于调整权重后的训练集训练下一个基学习器；如此重复进行，直至基学习器个数达到预先指定的值，或整个集成结果达到退出条件；最后将这些学习器进行加权结合。

梯度提升决策树(gradient boosting decision tree,GBDT)由Friedman[13]于2001年提出。GBDT的原理是利用梯度下降法，在之前所有树的基础上生成新树，并使目标函数尽可能小。XGBoost[14]是在GBDT的基础上进行诸多优化后得到的模型，可以在取得高精度的同时保持极快的识别速度。

XGBoost是由B个基学习器组成的加法模型。给定数据集U，共有n个样本，m个特征，U={(xi,yi)}，|U|=n,xi∈m,yi∈，XGBoost模型的预测结果[14]为

(8)

式中F={f(x)=wq(x)}(q∶m→G,G为树的叶节点个数)为回归树空间，其中x为数据集中样本的特征，q为每棵树的结构，这些树将样本映射到相应的叶节点，每个fb对应第b棵独立的树结构q和叶权重w∈G。与DT不同的是，每棵回归树在每片叶上都包含一个连续的得分，第i片叶上的得分为wi。对于一个给定的样本，利用由q给定的树的决策规则对该样本进行分类，将该样本的特征放入叶子中，通过将相应叶子中的分数相加，计算最终预测。

模型的损失函数f1和抑制模型复杂度的正则项Ω组成XGBoost的目标函数[14]，即

(9)

其中等号右边第2项的正则化项的具体表达式[14]为

(10)

2 双跨平面梁损伤演化监测数据生成

利用有限元软件构建双跨平面梁模型。该模型的边界条件为左下端固定铰支座，中间及右端为滑动铰支座，梁长度为10 m，高度为0.5 m，宽度为0.3 m，采用素混凝土作为有限元单元的材料，弹性模量为34.5 GPa，泊松比为0.2，热膨胀系数为10-5℃-1。损伤区域划分如下：模型长度方向划分50份，高度方向划分5份，顶板、底板分别均匀布置10个传感器，传感器分布如图1所示。

S1—标签为(L1，P1)的工况，L1为第1种损伤长度标签，P1为第1个损伤位置标签；S2—标签为(L2，P3)的工况，L2为第2种损伤长度标签，P3为第3个损伤位置标签；S3—标签为(L3，P5)的工况，L3为第3种损伤长度标签，P5为第5个损伤位置标签。图1 双跨平面梁模型、传感器分布和3个损伤工况实例

通过设置单元格刚度折损程度为99%进行损伤模拟，损伤宽度均为0.2 m，单损伤设置规则如下。

1)损伤位置：沿梁长度方向，除了两端以外的每个损伤区域单元分别设置一处损伤，共48个损伤位置，标签设置为P1，P2，…，P48。

2)损伤长度：损伤自梁底部向上发展，共3种损伤长度，即高度的20%、高度的40%、高度的60%，标签设置为L1、L2、L3。

由一个损伤位置和一个损伤长度组合为一个损伤工况，总工况个数为48×3=144，其中3个损伤工况实例S1、S2、S3如图1所示。

对数值模拟的双跨平面梁施加温度激励，底板温度设置为0 ℃，顶板温度设置为1 ℃，沿梁高度方向服从指数分布，纵坐标y处的温度Ty为

Ty=T1+T2e-5(0.5-y)，

(11)

式中：T1为底板温度；T2为顶板温度。

采用广东省肇庆市西江大桥的实测温度数据，每天03:00:00、09:00:00、15:00:00、21:00:00采样1次，共采集4 a温度数据，顶板、底板温度曲线如图2所示。

图2 广东省肇庆市西江大桥4 a顶板、底板温度曲线

为了使研究更符合实际，在模拟数据中加入信噪比Rsn为40 dB的干扰噪声，每个样本由20个测点数据以及损伤长度、损伤位置2个标签组成，每组工况共生成5 840个数据，并假定前2 920个数据对应无损状况，损伤在第2 921个数据点时发生，即后2 920个数据对应损伤状况。

标签为(L1，P3)的损伤工况的原始应变响应数据经MPCA所得第一、第二特征向量第一分量的时间序列如图3所示。从图中可以看出，第一、第二特征向量对损伤的发生反应明显，第一特征向量的分量数值在无损和损伤稳定期小幅波动，从损伤发生直至损伤稳定，分量数值大致保持线性变化；第二特征向量在无损和损伤稳定期，分量数值为震荡形式，从损伤发生到损伤稳定期，分量数值维持小范围波动；第三至二十特征向量在损伤前、后都为无规则震荡状态，没有发生人眼可辨的变化。为了减少数据的冗余，只对比第一特征向量Ψ1=(Ψ1,1,Ψ1,2,…,Ψ1,N)T、第二特征向量Ψ2=(Ψ2,1,Ψ2,2,…,Ψ2,N)T以及结合第一、第二特征向量Ψcomb=(Ψ1,1,Ψ1,2,…,Ψ1,N,Ψ2,1,Ψ2,2,…,Ψ2,N)T的组合特征向量这3种损伤指标在结构损伤识别中的优势。本文中所探究的是损伤初期的识别，因此特征向量只选取损伤发生后1 a的数据即损伤发生到损伤稳定的数据作为模型的训练、测试数据。

(a)第一特征向量第一分量Ψ1,1

3 结果与讨论

3.1 损伤指标

以信噪比Rsn分别为40、30、20、10 dB的4种强度噪声信号数据经MPCA所得特征向量作为输入，选取DT模型作为分类模型，对比第一、第二、组合特征向量损伤定量和损伤定位2种任务的识别性能。

3.1.1 损伤定量

准确率等于测试集中分类正确的样本个数除以测试集中总样本个数，由此计算不同强度噪声时以不同特征向量为输入的DT模型损伤定量的准确率，结果如表1所示。由表可知：在Rsn为40 dB，即噪声较弱时，第二特征向量比第一特征向量表现更优异，但是当噪声增强时，第一特征向量为输入时的准确率大于第二特征向量为输入时的准确率，表明第一特征向量的抗噪性好于第二特征向量的抗噪性；无论是强噪声还是弱噪声时，相对于单个特征向量，组合特征向量表现更优异。

表1 不同强度噪声时以不同特征向量为输入的决策树模型损伤定量的准确率

为了更详细地表征模型的识别结果，对Rsn分别为40、10 dB时弱噪声、强噪声条件下测试集中144个工况分别输出损伤定量准确率，不同特征向量训练所得损伤长度识别模型的识别结果如图4、5所示，其中每个方框(i,j)为测试集中标签为(Lj,Pi)的损伤工况的损伤定量准确率。以组合特征向量为输入时各工况损伤定量准确率减去以单个特征向量为输入时的准确率，可以得到组合特征向量训练所得损伤长度识别模型对单个特征向量训练所得模型的优化结果，如图6、7所示，其中在损伤位置标签P2、P7、P12、P17、P22、P27、P32、P37、P42、P47处布置传感器。

由图4—7可知：1)当噪声变强时，平面梁两端以及两两传感器之间位置处的损伤定量准确率急剧下降，原因是这些位置处损伤发生引起的传感器响应过小，噪声强度达到一定程度时会淹没损伤响应。2)强噪声时，第一、第二特征向量在传感器布置处的损伤定量性能相差较小，但是在平面梁两端或两两传感器之间的传感器响应较小的位置处，第二特征向量的性能远劣于第一特征向量的性能，验证了第一特征向量的抗噪性优于第二特征向量的抗噪性。3)弱噪声时，相对于第一特征向量，组合特征向量的损伤定量性能在几乎所有工况中都有所提升，准确率最高可提升11%；相对于第二特征向量，组合特征向量的损伤定量性能的改善主要表现在对平面梁两端位置处的损伤工况的识别，准确率最高可以提升21%。4)强噪声时，相对于第一特征向量，组合特征向量损伤定量性能的改善主要表现在对平面梁中间位置损伤工况的识别，准确率最高可提升28%，但是当损伤发生在平面梁两端的某些位置处时，第一特征向量的损伤定量准确率比组合特征向量的高，最大能高出22%；相对于第二特征向量，当损伤发生在2个传感器之间位置处时，组合特征向量的损伤定量准确率最高能提升63%，说明组合特征向量可以对远离传感器位置的损伤进行有效的识别。

(a)第一特征向量

(a)第一特征向量

(a)相对于第一特征向量为输入时的准确率提升

(a)相对于第一特征向量为输入时的准确率提升

综上，在损伤定量识别中，第一特征向量有良好的识别性能和优异的抗噪性，第二特征向量有优异的识别性能和较差的抗噪性。在一定强度的噪声条件下，组合特征向量具备2个特征向量的优点，并且能够克服单个特征向量的局限，从而达到优异的损伤识别性能和优异的抗噪性。当噪声强度超过界限时，虽然组合特征向量整体性能优于第一特征向量性能，但是在损伤响应小的某些位置，第一特征向量的损伤长度识别性能优于组合特征向量的损伤长度识别性能。

3.1.2 损伤定位

为了对比不同特征向量训练所得模型的损伤定位能力，计算不同强度噪声时以不同特征向量为输入的DT模型损伤定位的准确率，结果如表2所示。从表中可以看出，相对于第一特征向量，识别性能优异的第二特征向量在弱噪声时损伤定位准确率较高，但是在噪声增强后，第二特征向量的性能骤然劣化，第一特征向量还能保持一定的准确率；相对于单个特征向量，组合特征向量能在保证损伤定位性能的同时保证良好的抗噪性，无论是弱噪声还是强噪声时，整体性能都较优。以上结论与损伤定量识别结论相同。

表2 不同强度噪声时以不同特征向量为输入的决策树模型损伤定位的准确率

对Rsn分别为40、10 dB时弱噪声、强噪声条件下测试集中144个工况分别输出损伤定位准确率，不同特征向量训练所得损伤位置识别模型的识别结果如图8、9所示。以组合特征向量为输入时各工况损伤定位准确率减去单个特征向量为输入时的准确率，可以得到组合特征向量训练所得损伤位置识别模型对单个特征向量训练所得模型的优化结果，如图10、11所示。由图8—11可知：1)与损伤定量模型类似，在强噪声条件下，损伤定位模型在平面梁两端位置和两两传感器之间位置处的表现不佳，并且损伤长度越小，定位准确率越低。2)相对于单个特征向量，无论是弱噪声还是强噪声时，组合特征向量的损伤定位性能都较好。3)相对于第一特征向量，无论是弱噪声还是强噪声时，组合特征向量几乎所有工况的损伤定位性能都有所提升，准确率最高分别提升14%、21%。4)弱噪声时，相对于第二特征向量，组合特征向量在特定几个位置处工况的损伤定位准确率高58%左右，其余位置处的准确率保持持平，相差不超过1%；强噪声时，相对于第二特征向量，组合特征向量在平面梁两端或部分两两传感器之间位置处的损伤定位准确率较高，最高提升74%，但是在平面梁中间的两两传感器之间位置，当损伤长度较大时，第二特征向量的损伤定位准确率高于组合特征向量的，最高提升17%。

(a)第一特征向量

(a)第一特征向量

(a)相对于第一特征向量为输入时的准确率提升

(a)相对于第一特征向量为输入时的准确率提升

综上，在损伤定位识别中，第一特征向量表现出优异的抗噪性，第二特征向量表现出优异的损伤识别性能。在一定强度的噪声条件下，对于所有工况，组合特征向量的损伤定位性能都优于单个特征向量的损伤定位性能，但是当噪声较强时，在平面梁中间两两传感器之间一些特定位置发生长度较大的损伤，第二特征向量的识别性能优于组合特征向量的识别性能。

3.2 分类模型对比

将MPCA分别与DT、KNN、RF、XGBoost这4种分类模型进行组合，用于连续监测结构期间损伤识别，通过数据分析，对组合方法的适用性进行评估。

对第一、第二、组合特征向量3种损伤指标以及信噪比Rsn分别为40、30、20、10 dB这4种噪声强度进行组合，对比4种分类模型对应损伤定量和定位的准确率，结果如图12所示。从图中可以看出，对于DT、RF、XGBoost模型，3种损伤指标的表现都符合3.1.1、3.1.2节中的规律：弱噪声时第二特征向量性能优于第一特征向量性能，强噪声时第一特征向量性能优于第二特征向量性能，无论是弱噪声还是强噪声，组合特征向量都比单个特征向量表现优异。利用KNN进行分类时，组合特征向量并未比单个特征表现好，原因是高维空间中所有样本的距离都是趋于相等的，在这种情况下，利用欧氏距离公式计算样本之间的距离没有意义，因此基于KNN的分类方法在高维度时表现更差。从图中还可以看出，在不同强度的噪声时，4种分类模型中集成学习模型RF和XGBoost比传统机器学习DT和KNN表现更优异，表明MPCA与集成学习模型联合进行损伤识别更具有应用潜力，RF与XGBoost准确率相差较小。当Rsn为40 dB时，组合特征向量联合集成学习模型损伤定量准确率为98.9%，损伤定位准确率为99.0%；当Rsn为10 dB时，组合特征向量联合集成学习模型损伤定量准确率为82.3%，损伤定位准确率为73.2%。

4 结论

本文中提出一种联合移动主成分分析与集成学习的结构损伤识别方法，并利用双跨平面梁的仿真监测数据对该方法进行了验证，得到以下主要结论：

1)无论是损伤定量还是损伤定位，MPCA的第一特征向量都表现出优良的抗噪性，第二特征向量表现出优良的识别性能。

2)弱噪声时，组合特征向量具备第一、第二特征向量的优点，对于144个工况，组合特征向量的损伤定量和定位性能都优于2种单个特征向量的。

3)强噪声时，组合特征向量整体性能优于单个特征向量性能，但是在某些特定工况时表现不同：相对于组合特征向量，第一特征向量在平面梁两端位置处某些损伤工况的损伤定量性能较好，第二特征向量在平面梁中间两两传感器之间位置处某些损伤工况的损伤定位性能较好。

4)相对于传统机器学习模型DT、KNN，集成学习模型RF、XGBoost更适合与MPCA进行组合，在结构损伤识别中能达到更高的准确率。