基于优化模糊推理系统的电力变压器故障检测方法

游 溢，赵普志，刘 冬，晏致涛，刘欣鹏

(1.国网新疆电力有限公司电力科学研究院，新疆 乌鲁木齐 830011；2.国网新疆电力有限公司，新疆 乌鲁木齐 830011；3.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

三相电力变压器是现代电力网络中成本最高、最重要的组件之一，与电力系统的安全性和服务质量密切相关。当变压器运行不正常或出现故障时，会导致电力系统供电中断等问题，造成电力企业的巨大损失，给电力消费者带来不便。由于电力变压器的替换成本极高且较为耗时，因此需要对变压器进行正确维护，并对其运行状态进行监测[1-2]。

发生在三相电力变压器中的故障通常分为两大类，即内部短路缺陷和内部早期缺陷。浪涌电流测量和溶解气体分析法(DGAM)[3-4]常被用于三相电力变压器早期故障检测和分类。目前的DGAM包括Doenernberg比率法(DRM)、气相色谱分析法(GCM)[5]、IEC 60599方法[6]等。这些方法利用变压器油生成的不同气体的比率进行故障检测，将不同气体密度与特定量进行比较，以评估和测试油浸式三相电力变压器的工作状态。这些传统方法较为便利，但在检测准确度方面存在局限和缺陷，且容易受到噪声影响[7]。此外，评估结果在很大程度上依赖于专家和技术人员的经验。

随着人工智能技术的快速发展，越来越多的研究人员使用人工智能方法识别故障。文献[8]中提出一种基于帝国殖民竞争算法优化支持向量机(SVM)的变压器故障诊断模型，对SVM进行了非线性和多分类变换，建立了帝国殖民竞争算法优化支持向量机的非线性多分类模型。文献[9]中结合多层感知机神经网络(MLPNN)和人工免疫系统算法进行电力变压器中故障的识别和分类。文献[10]中引入灰太狼优化算法，并将差分进化机制引入到该算法中，提出一种基于改进的灰太狼优化算法(MGWO)和SVM的变压器故障诊断方法，能提供短周期和一般周期中故障率相关的实际信息，有助于提高变压器的运行可靠性。文献[11]中提出一种基于Mel时频谱-卷积神经网络的变压器铁芯松动声纹识别方法，采用基于Mel时频谱的噪声样本处理方法，搭建铁芯夹件松动故障模型，构建Mel时频谱-卷积神经网络，实现了铁芯松动故障的准确识别，但利用这种神经网络只能针对特定环境下的故障识别。文献[12]中提出一种基于深度判别受限玻尔兹曼机遗传算法优化的变压器故障诊断模型，将遗传算法进行全局优化，确定最优初始参数值，并在局部解空间对模型进行进一步训练。文献[13]中提出一种基于不精确概率的变压器故障诊断方法，诊断过程采用了不精确Dirichlet模型和朴素凭证分类器。

在上述故障识别的研究基础上有2个重要问题需要解决，即DGAM信息中最具指导性的属性以及分类器的类型。本文中提出一种基于一维卷积神经网络(1D-CNN)[14]和优化自适应神经模糊推理系统(ANFIS)的电力变压器故障检测方法(简称本文方法)，采用1D-CNN选择最具指导性的属性，并将输入数据维度最小化，同时使用ANFIS作为主分类器。为了改善ANFIS的性能，采用改进帝王蝶优化算法(IMBO)进行电力变压器故障分类，通过实验验证本文方法的优越性能。

1 基于1D-CNN的最优属性选择

在DGAM得到的属性中，弱指导性属性作为人工噪声会导致性能劣化，降低故障分类准确度，为此，必须从数据库中移除无信息属性，仅使用有效属性作为系统的输入。本文中采用1D-CNN在多个属性中选择最优属性，目的是提高识别准确度，缩短运行时间。众所周知，二维卷积神经网络(2D-CNN)已广泛用于图像识别任务，取得了很好的效果。1D-CNN广泛用于序列模型，其卷积层使用一维互相关操作，并且一维全局最大池化层可以减少分类器或预测模型的特征维数。1D-CNN的结构如图1所示。

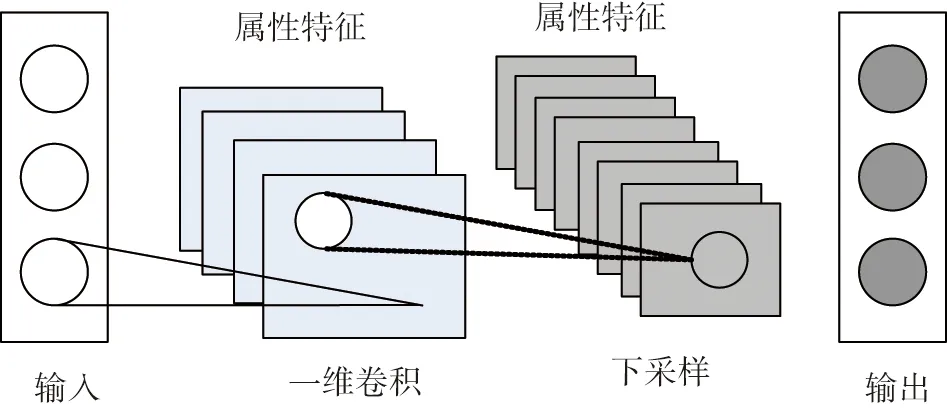
图1 一维卷积神经网络结构示意图

1D-CNN的卷积作用是从DGAM得到的属性中提取最优的属性特征，将不同大小的卷积核应用到属性特征中，以捕捉最优属性特征。生成的属性特征为

hd,t=tanh(Wdxt∶t+d-1+bd)，

(1)

式中：hd,t为卷积神经网络生成的属性特征，d为步长，t为时间窗口的起始点；xt∶t+d-1为t到t+d的窗口的输入特征向量；Wd为可学习权重矩阵；bd为偏差。在每个卷积中，对卷积核大小为d的属性图进行最大超限时间(max-overtime)池化，最终得到最优属性特征。

采集的变压器故障数据集中包含4类故障数据，分别为局部放电故障(PDF)、能量放电故障(EDF)、过热故障(OHF)和无故障(NF)。利用关联规则(AR)找到PDF、EDF、OHF、NF类的大项集，即

输入：1、2、4和12(NF类的大项集)；

输入：5、8和12(PDF类的大项集)；

输入：2、5和8(EDF类的大项集)；

输入：1、3、4和11(OHF类的大项集)。

由该大项集可知，输入参数1、2、4和12可以定义NF类故障，输入参数5、8和12可以定义PDF类故障，输入参数2、5和8可以定义EDF类故障，输入参数1、3、4和11可以定义OHF类故障。对于变压器故障检测和分类，这些特征是最重要、最具信息量的特征，因此，本文中仅使用其中8个特征作为ANFIS的输入。这8个特征分别是氢气(H2)、甲烷(CH4)、乙烯(C2H4)、乙烷(C2H6)、乙炔(C2H2)、C2H4或C2H6、CH4或CH2-C2H2-C2H4、C2H4或CH4-C2H2-C2H4，分别记为Atr,1、Atr,2、Atr,3、Atr,4、Atr,5、Atr,8、Atr,11、Atr,12。

使用1D-CNN的优势是能够降低分类器或自适应神经模糊推理预测模型的输入特征维数，且具有非常高的识别准确度。

2 基于ANFIS和IMBO的分类

首先从数据库中移除无信息属性，采用有效属性作为输入，通过1D-CNN选择最优属性集，将ANFIS 的输入数据容量从14个 (未处理数据状态) 减少至较少数量(使用选择的属性)。从14个原始属性中选出M个属性，Atr，s表示被选择的属性，s为输入数据的序号，且s=1,2,…,M，M≤14，如图2所示。

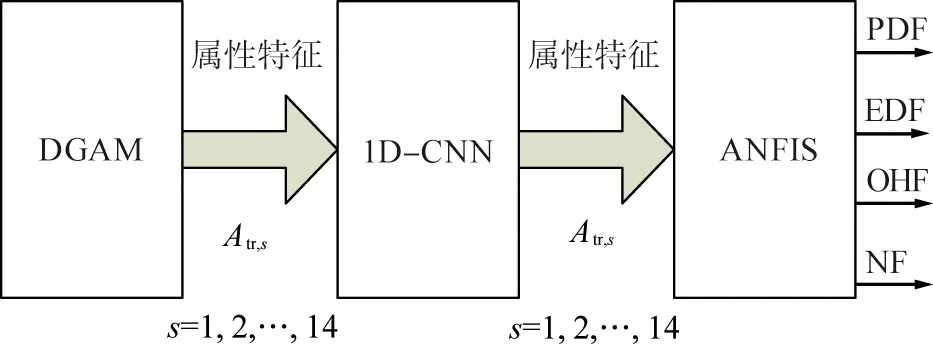
DGAM—浪涌电流测量和溶解气体分析法；1D-CNN—一维卷积神经网络；ANFIS—自适应神经模糊推理系统；PDF—局部放电故障；EDF—能量放电故障；OHF—过热故障；NF—无故障；Atr,s—被选择的属性，s—输入数据的序号。图2 电力变压器故障检测算法的属性选择

在ANFIS中，初始未知参数的数值决定分类任务的准确度。本文中的ANFIS结构共分为5层，如图3所示，各层的功能如下：第1层利用隶属函数和节点模糊集制定一个新的隶属度；第2层利用某些乘数乘以输入信号的数量；第3层中的每个节点均为静态的，表示为标准节点(NORM)，某个节点数值为该节点触发强度与所有规则强度之和(SUM)的比值；第4层给出上一层输出的归一化处理结果；第5层给出ANFIS的最终预测结果。总的来说，第1—3层是规则前件，第4—5层是规则后件。

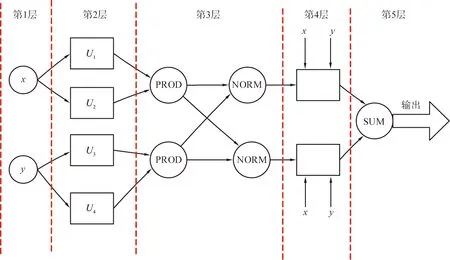
PROD—点积；NORM—标准节点；SUM—求和；x—系统输入；y—系统输出；U1、U2、U3、U4—模糊集的元素。图3 自适应神经模糊推理系统结构示意图

传统的ANFIS使用基于梯度的算法作为学习算法，但存在一些固有缺陷，例如收敛较慢，很容易陷入局部极小值等。此外，基于梯度的算法中随机初始解在很大程度上决定了算法的成功与否，并且在初始解较弱或不合适的情况下会导向局部极小值，造成ANFIS的训练失败[15]，因此，本文中使用IMBO改善ANFIS的性能。

帝王蝶优化算法(MBO)[16]是一种基于种群的启发式算法，根据北美地区的蝴蝶迁徙行为而开发的。帝王蝶每年迁徙2次，第1次迁徙从加拿大至墨西哥，第2次迁徙从墨西哥至加拿大。启发式算法通过模拟帝王蝶的迁徙行为来获得优化问题的求解。与其他优化算法类似，MBO先从搜索空间中的随机种群出发，并利用一些策略来逼近全局解。MBO的详细说明可参阅文献[16-17]。

MBO的缺点是随机选择个体来产生新的个体，容易造成信息丢失或者陷入局部最优。为了提高求解质量，实现种群的合作和竞争，本文中选取5个差分变异策略，即

(2)

式中：V1、V2，…，V5分别采用5个差分变异策略产生的新变异个体；Xr1、Xr2、Xr3、Xr4分别为来自于父代的4个不同个体；Xbest为当前最优个体；λ、F为缩放因子，取值范围均为[0,2]。差分变异策略的作用是在一定程度上增加种群的记忆性和共享信息[18]，提高算法最优解的准确性。

对于本文中的求解问题，隶属函数的类型取决于问题特性，应由设计者进行选择。先前的参数有(a1,1,b1,1,c1,1),(a1,2,b1,2,c1,2),… ,(aN,M,bN,M,cN,M)，其中，(aN,M,bN,M,cN,M)表示第N个输入变量的第M个隶属函数的参数。输入变量个数N取决于要分析的问题，描述每个数据的隶属函数的数量M由设计者决定。结论参数有(p1,q1,r1),(p2,q2,r2),…,(pK,qK,rK)，其中p、q、r为规则后件参数，K为模糊规则个数。结论参数的数量取决于模糊规则个数。

3 仿真结果与分析

仿真实验在配置了英特尔酷睿i7处理器，主频为2.8 GHz，容量为16 GB随机存取存储器(RAM)的计算机上进行。使用MATLAB 2011b编程环境进行仿真，将50%的数据用于训练，50%的数据用于测试。所有结果均取50次独立运行的均值。若标准偏差(SD)较小，则表明分类器具有较高的稳健性和可靠性。

3.1 数据集

对利用DGAM得到的信息进行解读，是电力变压器内部故障的识别和分类的常用手段之一。由于变压器内部故障和状态不同，因此变压器油中生成和分解出的气体不同，主要有C2H6、C2H2、C2H4、CH4、H2[19]。信息解读就是利用不同生成气体的比例进行变压器内部缺陷的检测和分类。文献[19]中提出的检测方法中使用的14个输入属性(数据集1)如表1所示。

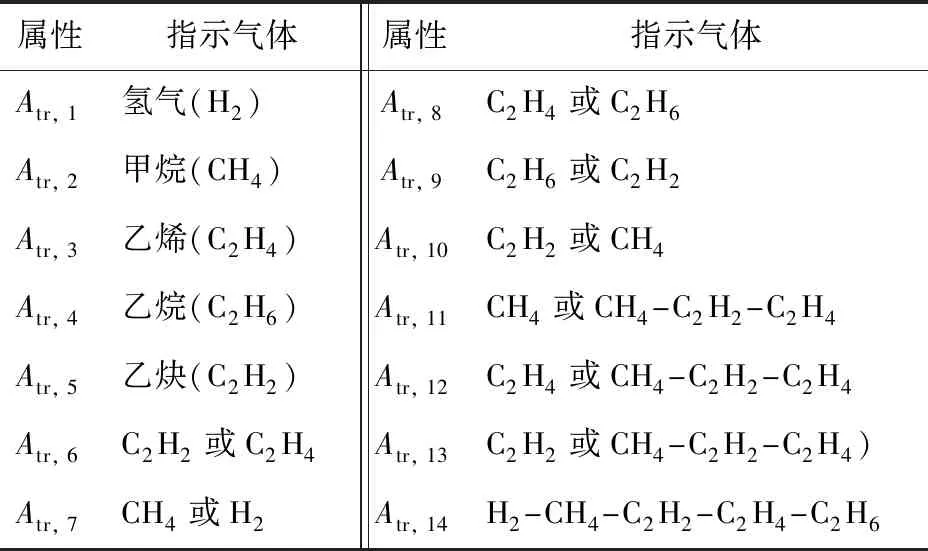
表1 电力变压器故障诊断时使用的属性

为了提高仿真实验的准确性和实践性，采用一个真实的变压器故障数据集[20]对本文方法进行性能评估。变压器故障数据集(数据集2)分类如表2所示。

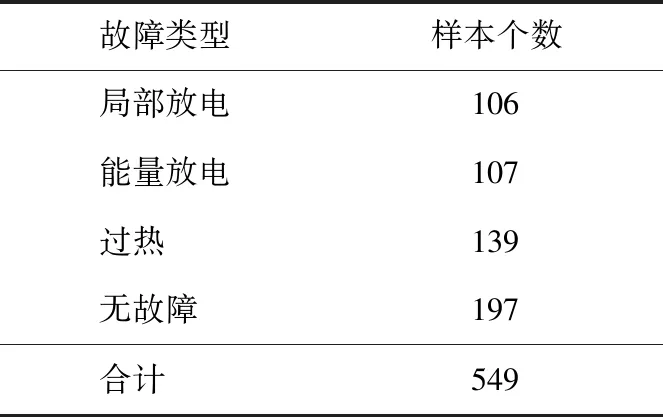
表2 电力变压器故障分类及样本个数

3.2 性能分析

选择表1中的8个属性作为ANFIS的最优输入。通过IMBO选择ANFIS的前因参数和结论参数，分类结果如表3所示，并与采用梯度算法得到相关参数的ANFIS(梯度ANFIS)进行对比。此外，为了分析1D-CNN的有效性，采用不同的特征属性作为ANFIS的输入。从表中可以看出，在数据集1中，采用本文方法以及输入第1—5个属性、第6—14个属性及全部14个属性得出的分类准确率分别为95.02%、95.91%和97.59%，而使用本文方法以及输入所选择的8个特征属性得到的分类准确率为98.91%，实验结果证明了属性选择和学习算法的有效性。从表中还可以看出，本文方法的标准偏差值为±0.01，表明本文方法性能优秀，稳健性高。

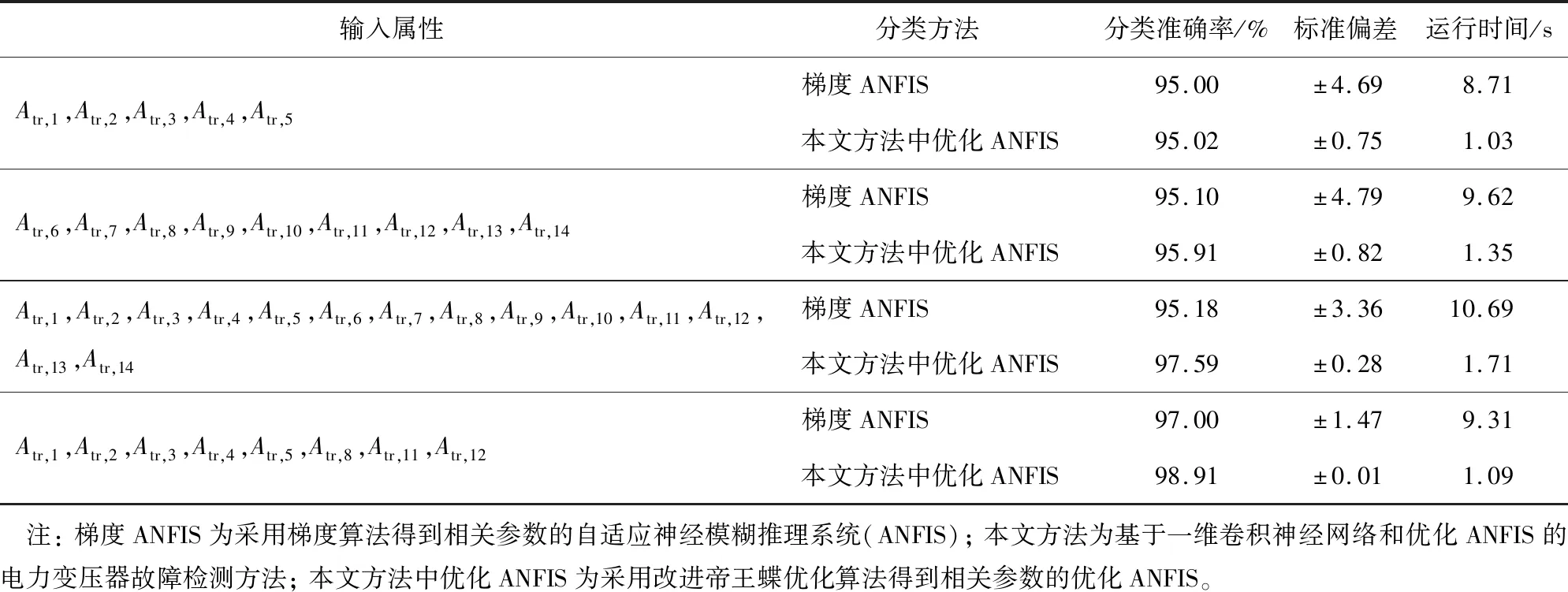
表3 不同算法在数据集1上的分类性能

将本文方法与文献[8]中提出基于帝国殖民竞争算法(ICA)优化支持向量机的变压器故障诊断模型(ICA-SVM)、文献[9]中提出的多层感知机神经网络(MLPNN)和人工免疫系统算法以及文献[10]中提出的基于MGWO和SVM的变压器故障诊断方法(MGWO-SVM)应用于同一数据集中，对故障检测性能进行对比，检测结果如表4所示。由于不同算法输入的属性不同，因此表中仅给出了每个算法得出的最优结果。从表中可以看出，本文方法在数据集2上取得了最优故障准确率，标准偏差更小，识别运行时间更短，检测方法的稳健性更高。

表4 不同算法在数据集2上的变压器故障检测性能

图4所示为IMBO和基于梯度学习算法在训练阶段的迭代次数与均方差的关系。从图中可以看出，IMBO的性能显著优于基于梯度的学习算法的，IMBO比梯度学习算法的均方差更小，并且需要更少迭代次数即可达到稳定的均方差。

图5所示为对于第1个输入变量，通过IMBO和基于梯度的学习算法建立的隶属度函数。从图中可以看出，通过不同算法建立的隶属度函数会导向不同的参数，而隶属度函数之间的细微差异则会导致不同的识别准确度。

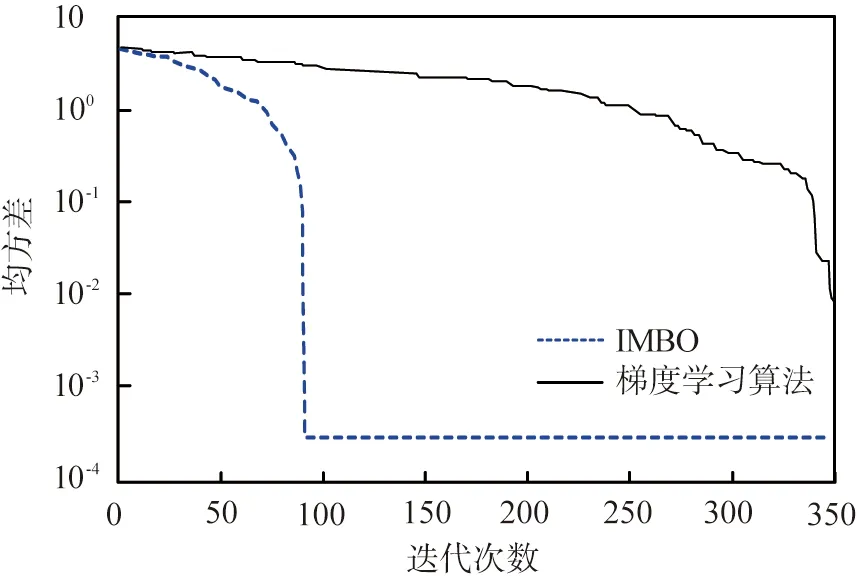
IMBO—改进帝王蝶优化算法。图4 不同算法在训练阶段的迭代次数与均方差的关系

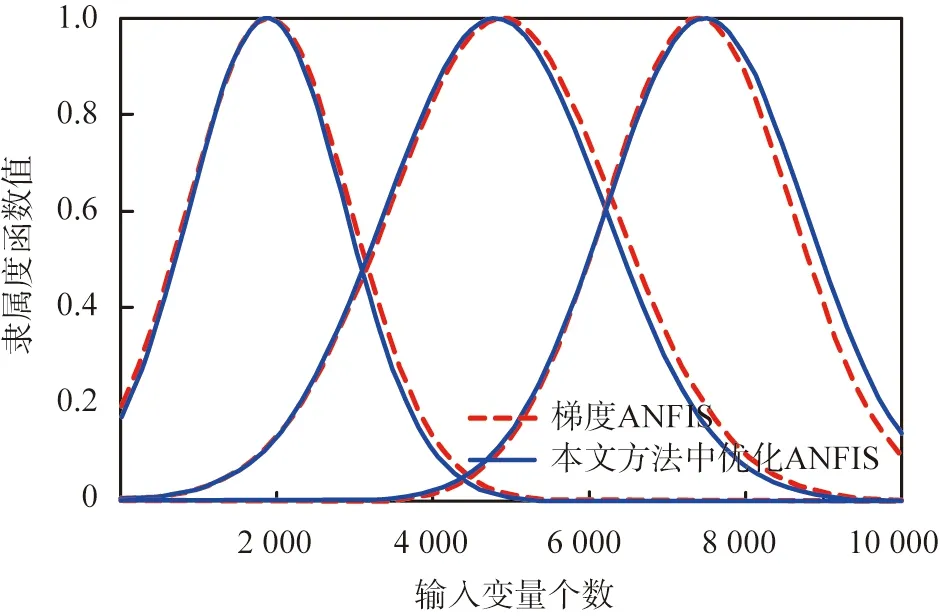
梯度ANFIS—采用梯度算法得到相关参数的自适应神经模糊推理系统(ANFIS)；本文方法—基于一维卷积神经网络和优化ANFIS的电力变压器故障检测方法；本文方法中优化ANFIS—采用改进帝王蝶优化算法得到相关参数的优化ANFIS。图5 采用不同算法建立的隶属度函数

IMBO的搜索收敛结果如图6所示。从图中可以看出，IMBO具有非常快的收敛速度，ANFIS参数从第1次迭代到预定义的最大迭代次数之间逐步变化，在第57次迭代后无明显变化。事实上，在第57次迭代后，扩散值达到稳定状态，算法已经到达了最优。

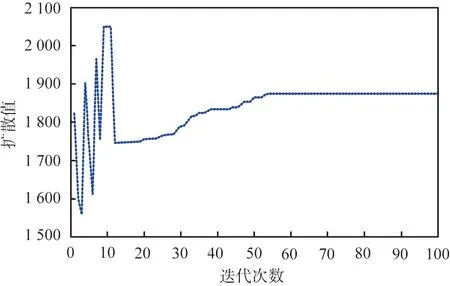
图6 改进帝王蝶优化算法的搜索收敛结果

4 结语

本文中提出了基于优化模糊推理系统的电力变压器故障准确诊断的可靠方案。采用1D-CNN选择从DGAM得到的最有效的属性，其中1D-CNN可以选择最有价值、最具指导性的属性，以最大限度减少输入变量的数量，降低计算负担。此外，为了得到ANFIS的最优参数，本文中采用了性能优良的改进型启发式算法IMBO。检测实验结果表明，与其他变压器故障检测方法相比，本文中提出的方法准确度更高，运行时间更短，稳健性更高，因此，1D-CNN与基于IMBO的ANFIS优化分类器相结合，可以改进ANFIS的准确度和稳健性。未来将进一步研究非DGAM信息的变压器故障检测分类问题，使检测算法具有更好的普适性。