基于多目标遗传算法的高速电梯垂直振动参数优化设计

赖永星，武 俊，王 珂

(郑州大学 力学与安全工程学院，河南 郑州 450001)

随着我国城市化进程的加快，高层建筑不断涌现，对高速电梯的需求量越来越大，因此对电梯运行平稳性和舒适性的要求也越来越高。电梯的垂直振动是衡量电梯平稳性和舒适性的重要指标，对于高速和超高速电梯来说，电梯垂直振动的振源主要来自于启制动过程中的惯性力和曳引轮旋转失衡造成的激振力。张长友等[1]建立系统多自由度电梯振动模型，阐述电梯系统提升过程中求解固有频率的方法，通过电梯运行实例分析，得出可以通过调节绳头弹簧刚度，使系统避开由曳引机旋转失衡引起的共振的结论。常娜[2]利用MATLAB软件进行分析和计算，提出电梯垂直振动系统运行状态和结构参数发生变化时的减振策略，并通过仿真验证了减振效果。郑有木[3]基于耦合推广正交算法对高速电梯模型进行分析，实现了电梯运行过程的平稳性性能指标优化。同时，一些研究[4-5]结合ANSYS、SolidWorks等软件对电梯系统进行减振设计。Sato等[6]提出一种新型磁流变阻尼器减振装置，主要运用于电梯紧急制动阶段，通过控制磁场实现阻尼变化，抑制电梯振动，保护乘客安全。Dai等[7]基于可变静态存储控制器的主动控制策略，考虑钢丝绳的几何非线性及边界条件，利用Ritz-Galerkin方法建立动力学方程和控制方程，并通过数值方法验证控制策略的有效性。

目前的研究大多通过调节单个系统参数，改变系统固有频率，避免共振，从而抑制电梯垂直振动。为了避免电梯垂直振动系统固有频率与激振力频率发生共振，降低激振力和起制动阶段产生的惯性力对垂直振动的影响，本文中以某型号曳引式高速电梯为研究对象，建立垂直方向的多参数电梯振动模型，将系统的刚度作为变量参数，同时考虑避免系统共振、轿厢的位移限制等作为约束条件，采用多目标遗传算法对电梯垂直振动系统进行多目标优化，获得系统刚度的最优解集。

1 电梯垂直振动系统

1.1 动力学模型

本文中研究的实验电梯为曳引比是2∶1的电梯，该电梯由承重梁承担总质量的1/2，相对于曳引比为1∶1的电梯，对曳引机功率要求较低，可以缩减曳引机的尺寸和规格，从而控制成本。电梯以曳引机为驱动，轿厢和对重侧各有一个动滑轮，通过曳引绳相连接。与电梯垂直振动系统中其他构件(轿厢轿架、对重)相比，曳引绳质量所占比例较小，可以忽略，仅将曳引绳等效为弹簧，考虑其刚度和阻尼。同时忽略电梯中电缆和限速器等的质量和转动惯量的影响。电梯垂直振动系统动力学模型结构简图如图1[8]所示，电梯垂直振动系统动力学模型中的有关参数如表1所示。

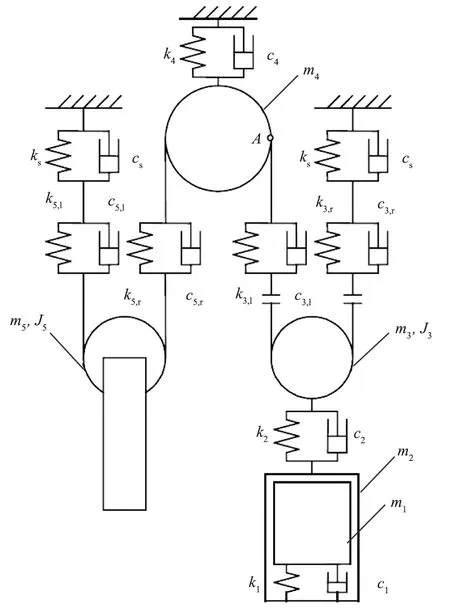
m1—轿厢及其承载质量；k1、c1—轿厢底减振橡胶刚度、阻尼；m2—轿厢架质量；k2、c2—轿顶轮与轿架连接弹簧刚度、阻尼；m3、J3—轿顶轮质量、转动惯量；k3，l、c3，l、k3，r、c3，r—轿厢左、右两侧钢丝绳等效刚度、阻尼；m4—曳引系统质量；k4、c4—曳引系统承重梁及减振橡胶垫等效刚度、阻尼；m5、J5—对重上方滑轮质量、转动惯量；k5，l、c5，l、k5，r、c5，r—对重左、右两侧钢丝绳等效刚度、阻尼；ks、cs—绳头等效弹簧刚度、阻尼。图1 电梯垂直振动系统动力学模型结构简图[8]

1.2 动力学方程

根据电梯垂直振动系统动力学模型，利用拉格朗日方程建立电梯垂直系统动力学方程，即

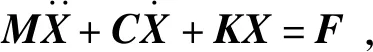
(1)

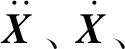
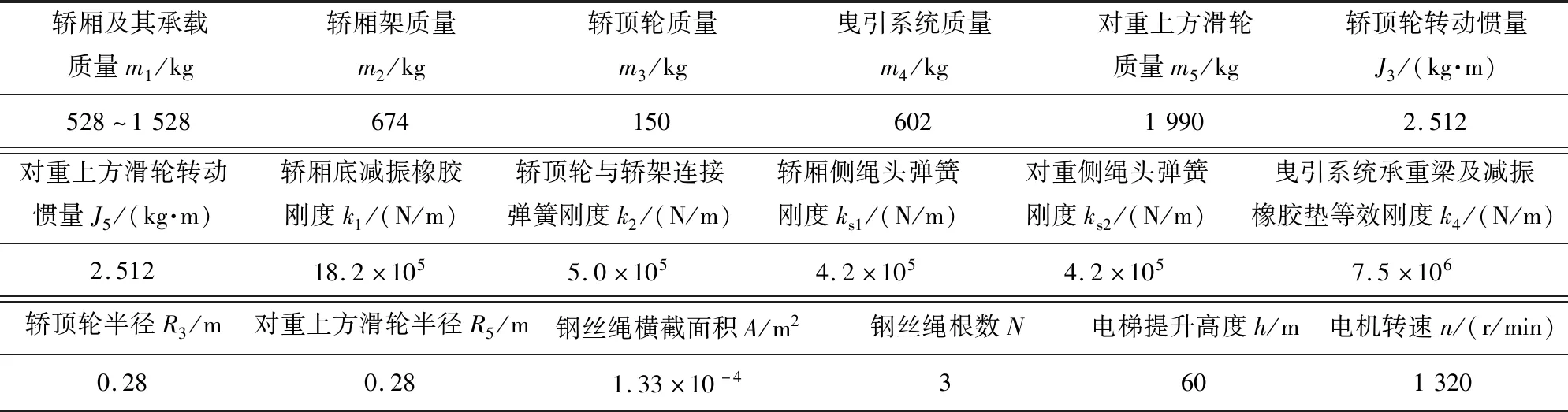
表1 电梯垂直振动系统动力学模型中的有关参数

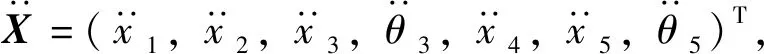
(2)

(3)

X=(x1,x2,x3,θ3,x4,x5,θ5)T，

(4)

M=diag(m1,m2,m3,J3,m4,m5,J5)T，

(5)

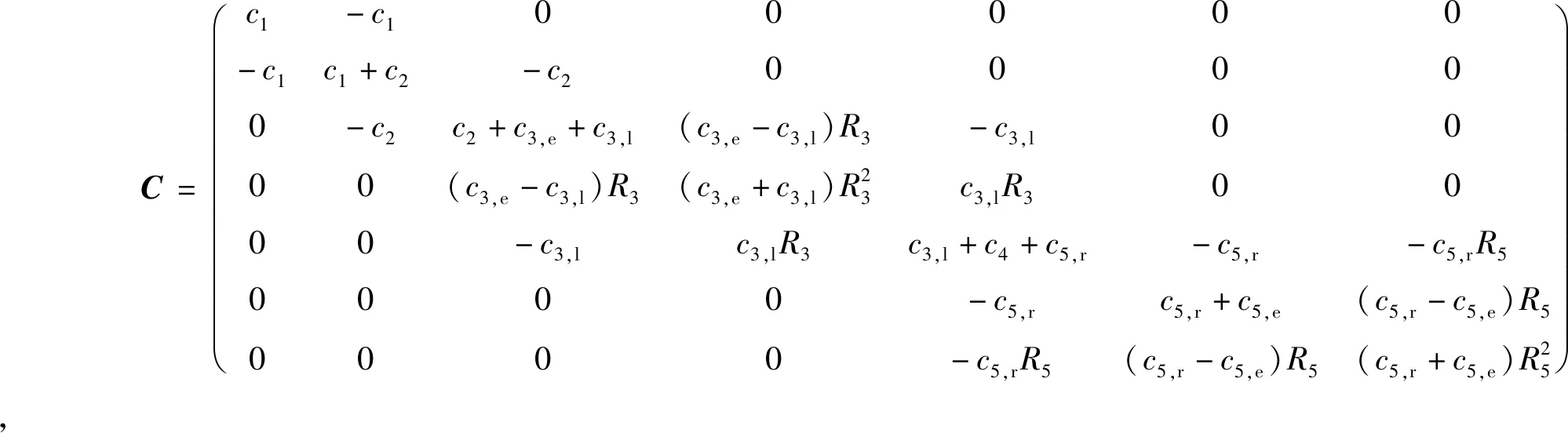
(6)

(7)

其中m1、x1为轿厢及其承载质量、线位移，k1、c1为轿厢底减振橡胶刚度、阻尼，m2、x2为轿厢架质量、线位移，k2、c2为轿顶轮与轿架连接弹簧刚度、阻尼，m3、J3、x3、θ3为轿顶轮质量、转动惯量、线位移、角位移，k3,l、c3,l、k3,r、c3,r为轿厢侧左、右两侧钢丝绳等效刚度、阻尼，m4、x4为曳引系统质量、线位移，k4、c4为曳引系统承重梁及减振橡胶垫等效刚度、阻尼，m5、J5、x5、θ5为对重上方滑轮质量、转动惯量、线位移、角位移，k5,l、c5,l、k5,r、c5,r为对重两侧钢丝绳等效刚度、阻尼，ks、cs为绳头等效弹簧刚度、阻尼；k3,e、c3,e为轿厢右侧曳引钢丝绳等效刚度、阻尼，k5,e、c5,e为对重右侧曳引钢丝绳等效刚度、阻尼，R3为轿顶轮半径，R5为对重上方滑轮半径。

在刚度矩阵中，钢丝绳的刚度k可以依据公式k=EA/L进行计算，其中E、A、L分别为钢丝绳的弹性模量、横截面积、长度，E=8.0×1010N/m2。

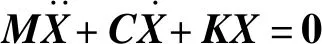
K=ω2M，

(8)

式中ω为系统的固有频率。

线性定常系统的固有频率可利用式(8)直接求解，但是运行中的电梯是时变系统，轿厢位置的变化导致曳引绳长度发生改变，刚度矩阵K中的参数k3,r、k3,l、k5,e、k5,r等不是定值，使得轿厢右侧曳引钢丝绳等效刚度k3,e=ksk3,r/(ks+k3,r)和对重左侧曳引钢丝绳刚度k5,e=ksk5,l/(ks+k5,l)时刻变化。利用式(1)并通过MATLAB软件编程，可以求出电梯在空载、半载、满载3种典型工况时前7阶固有频率。

在兼顾电梯乘客乘坐舒适性和电梯提升效率的基础上，设置高速电梯提升系统的电梯运行参数，本文中使用典型电梯运行参数[2]，电梯从底层启动到t1时间段是变加速度运动过程，当时间为t1时，速度达到最大值，开始进行匀速运动，当时间为t2时，系统进入制动阶段，最后当时间为t3时，到达顶层而停止运行。高速电梯运行中的加速度、速度、位移曲线如图2所示。

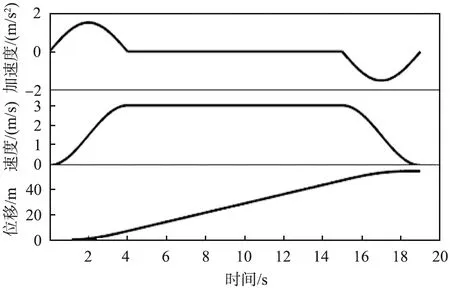
图2 高速电梯运行中的加速度、速度、位移曲线

1.3 模态分析

根据表1中电梯的基本参数，可以求得空载、中载、满载3种典型工况时电梯垂直振动系统前7阶固有频率的变化，如图3所示。从图中可以看出，电梯垂直振动系统前7阶固有频率具有以下特点：

1)电梯系统的固有频率随轿厢载重增加而减小，载重的变化对低阶固有频率(1、2、4阶)改变量较大，而对高阶固有频率(5、6、7阶)的影响较小。

2)在电梯系统运行过程中，低阶固有频率(1、3、4、5阶)随轿厢位置上升而增大。第2阶固有频率随轿厢位置上升而减小，原因是第2阶固有频率是以对重为主的振型振动形态。高阶固有频率(6、7阶)受轿厢位置影响较大，具有很强的波动性。

3)系统的各阶固有频率不是恒定值，受电梯提升高度及载重的变化而变化。除了第7阶固有频率较大外，其余各阶固有频率均小于35 Hz，并且在电梯运行中不会与曳引机激振力(根据表1求得曳引机激振力频率为22 Hz)发生共振。

2 多目标遗传算法在电梯垂直振动系统中的运用

遗传算法(GA)是根据大自然中生物体进化规律而提出的。该算法通过数学推导和计算机仿真运算,将需要求解的过程转化为生物进化中染色体基因的交叉和变异过程。相对于常规的优化算法，该算法能较好、更快地求解较复杂的组合优化问题，因此广泛应用于机器学习、控制系统、信号处理及人工智能。

高速电梯的运行过程是涉及多自由度且各自由度相互耦合的复杂过程，采用单一目标优化方法难以实现电梯垂直振动系统的减振优化设计，因此以某高速电梯为研究对象，以提高电梯舒适性及安全性为目的，采用多目标遗传算法，对电梯垂直振动系统进行系统参数优化，获取系统参数对电梯垂直振动系统动态特性的影响规律及最优解集。

2.1 选取目标函数

高速电梯的垂直振动是影响电梯乘坐舒适性及安全性的主要因素，也是电梯制造、生产、安装及维护时关注的重点。垂直振动中的加速度及加速度变化率通常是乘坐电梯舒适性和安全性的主要因素和指标。

由于加速度相对于其他物理量较容易测量，因此可以通过加速度及加速度变化率衡量电梯系统的振动指标。根据国家标准GB/T 10058—2009《电梯技术条件》[9]和文献[10-11]，对于高速电梯和超高速电梯，运动特性和振动舒适性指标应控制在一定范围内，高速电梯和超高速电梯的运动特性和振动舒适性指标如表2所示。

综合考虑电梯轿厢提升过程中舒适性指标，对电梯垂直振动系统参数进行优化设计。以0～4 s启动加速阶段轿厢振动加速度均方根值为轿厢舒适性目标函数f1(X)，其中X为系统位移，以4～8 s匀速阶段轿厢振动加速度均方根值为轿厢舒适性目标函数f2(X)，以8～13 s匀速阶段轿厢振动加速度均方根值为轿厢舒适性目标函数f3(X)，以15～19 s 制动减速阶段轿厢振动加速度均方根值为轿厢舒适性目标函数f4(X)。为了兼顾电梯轿厢提升过程中各阶段的平稳性和舒适性，需要使单一目标函数值均较小，因此采用线性加权组合方式处理各阶段的单一目标函数，将多目标函数转化为单目标函数f(X)进行求解[12-13]，得到单目标优化模型，即

(9)

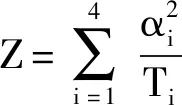
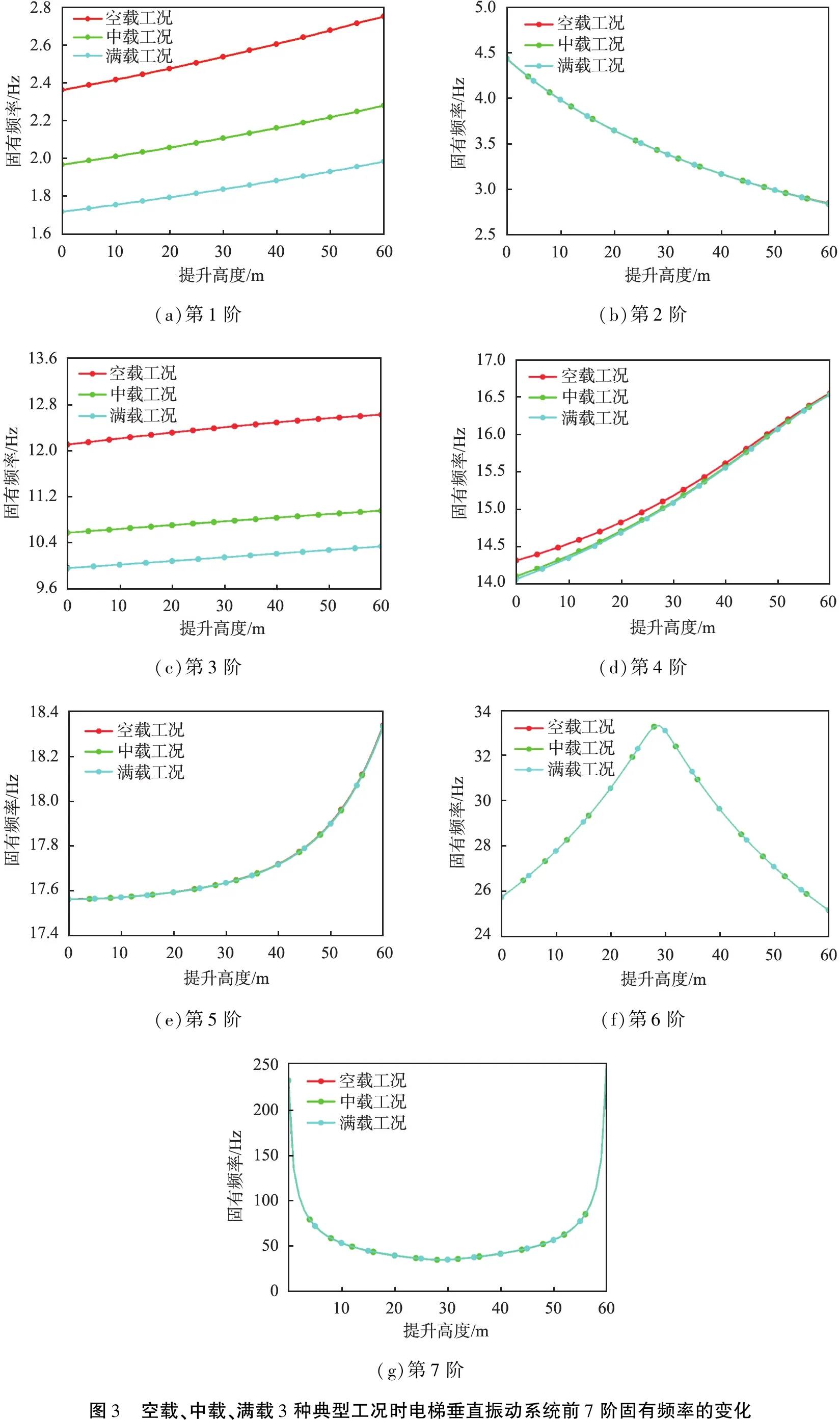
表2 高速电梯和超高速电梯的运动特性和振动舒适性指标

2.2 设计参数

影响电梯垂直振动系统瞬态加速度响应的变量主要有轿厢底减振橡胶刚度k1、轿顶轮与轿架连接弹簧刚度k2、曳引系统承重梁及减振橡胶垫的等效刚度k4、轿厢侧绳头弹簧刚度ks1、对重侧绳头弹簧刚度ks2[2]。电梯垂直振动系统设计参数如表3所示。

表3 电梯垂直振动系统设计参数

2.3 约束条件

为了使电梯在高速运行中避免出现共振现象，电梯系统各阶固有频率应远小于或远大于曳引机激振力频率；同时，轿厢及轿厢架之间的相对位移也受到轿厢架规格的限制。由此可得约束条件为

(1.1f-ω)(0.9f-ω)≥0，

(10)

xmax≤15 mm，

(11)

式中：f为曳引机旋转失衡引起的激振力频率；ω为电梯提升过程中系统各阶固有频率；xmax为最大振动位移响应。

2.4 优化过程及结果

采用满载工况对电梯垂直振动系统进行多参数动力学优化。多目标遗传算法初始化参数设置如下：种群数量为20，初始迭代次数为1，最大迭代次数为200，交叉概率为0.9，变异概率为0.1，产生初始种群后进行遗传迭代，将所有约束条件作为检验函数进行求解，计算出最优解，电梯垂直振动系统多目标遗传算法流程如图4所示。

当算法进化到第68代时，目标函数收敛到最优，电梯轿厢振动加速度目标函数值随多目标遗传算法迭代次数的变化如图5所示，最终得到多目标遗传算法电梯垂直振动系统各刚度参数优化结果，如表4所示。

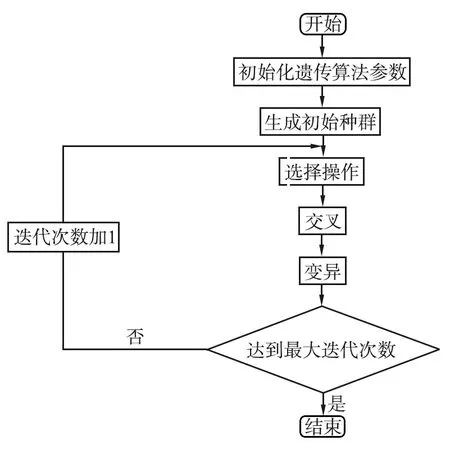
图4 电梯垂直振动系统多目标遗传算法流程

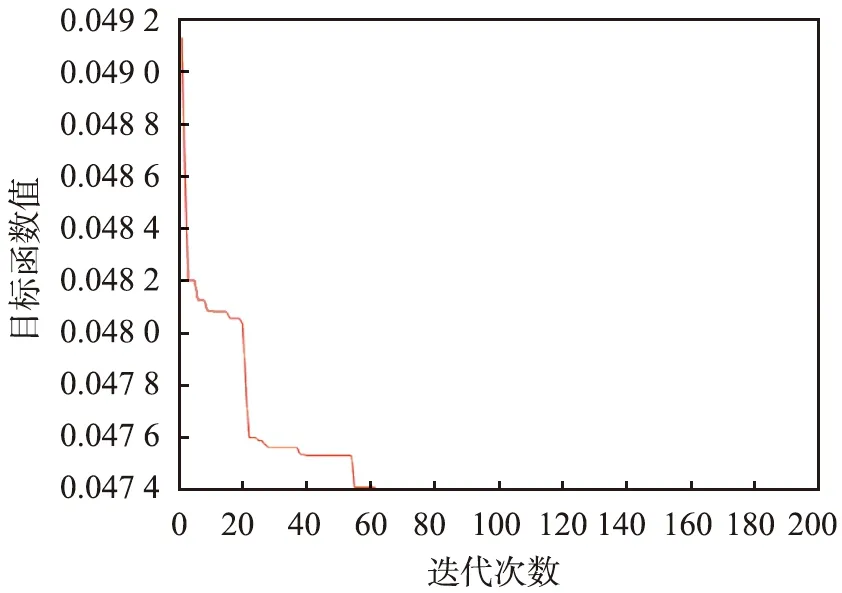
图5 电梯轿厢振动加速度目标函数值随多目标遗传算法迭代次数的变化

表4 多目标遗传算法电梯垂直振动系统 各刚度参数优化结果

3 参数改变前、后电梯系统瞬态响应对比

根据多目标遗传算法对电梯垂直振动系统的优化，由表4中电梯垂直振动系统刚度参数优化结果，得到优化前、后电梯轿厢的振动加速度和振动位移，如图6、7所示。优化前、后电梯轿厢垂直振动的峰值振动加速度如表5所示。由图6、7及表5可知，通过优化电梯垂直振动系统刚度参数，电梯轿厢在运行各阶段振动加速度均有所改善，其中匀速阶段和制动阶段均满足舒适性指标，启动阶段的振动加速度也得到优化，轿厢的振动位移得到有效抑制。由此可知，本文中提出的基于多目标遗传算法的电梯垂直振动参数优化方法能有效抑制电梯高速运行中的振动。

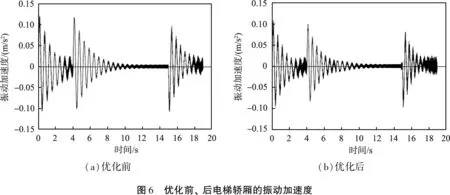
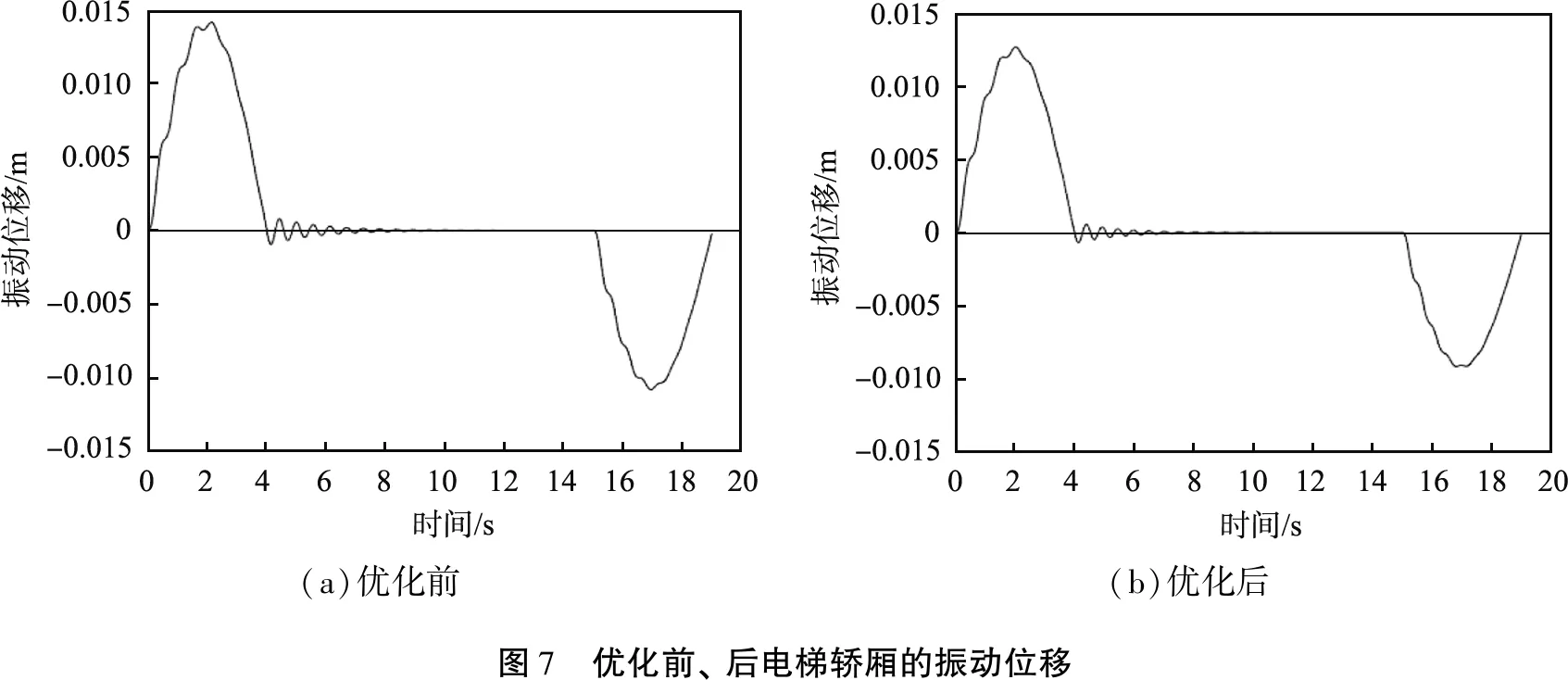
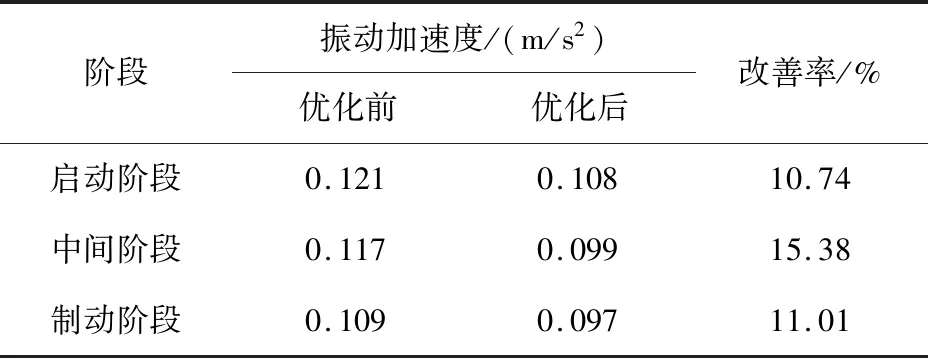
表5 优化前、后电梯轿厢垂直振动的峰值振动加速度

4 结论

本文中建立了受外部激振力即起制动过程中惯性力和曳引轮旋转失衡产生的激振力的电梯垂直振动系统模型及非线性振动微分方程，通过模态分析及多目标遗传算法，研究电梯垂直振动系统参数对电梯振动的影响，为电梯的设计与减振提供了依据。

1)以实际电梯为模型，建立七自由度电梯垂直振动系统动力学模型，并利用MATLAB软件得出固有频率随系统参数的变化规律。

2)多目标遗传算法能够获得系统参数的优化方案，经过多参数优化后，电梯轿厢在运行过程中振动加速度幅值达到舒适性指标要求。

3)与仅改变单一刚度参数方法相比，多参数系统遗传算法减振方案更接近全局最优解，方法快速、可靠，为高速电梯提升系统的动力学行为以及变参数振动控制的深入分析提供了途径和方法。