基于离散元法的二元颗粒流剪切分离机理分析

黄仕昭，郑 麟，李玉秀，陈 颖

(1. 广东工业大学 材料与能源学院，广东 广州 510006；2. 浙江大学 能源工程学院，浙江 杭州 310013)

颗粒系统在静止时表现出固体的性质，但是因内部耗散效应的存在而区别于固体。在稀疏颗粒流中，颗粒碰撞和作用时间较短，表现出流体的性质；而在致密颗粒流中，颗粒持续接触碰撞，既表现出固体的特征，又存在流体的性质。在工业生产中，因对颗粒相互作用机理缺乏认识而产生了许多问题。例如，在材料制备过程中，压制的材料因均匀性缺陷而不具备理想的性能；在药物运输过程中，震动导致药物颗粒分离；在粉体材料的管道输运中，颗粒在静电作用下聚集，引起管道阻塞。除此之外，谷仓堆积、采矿、泥石流、雪崩、河床泥沙堆积、管道拥堵等一系列问题的解决都需要掌握颗粒的作用机制，从而解决工业生产中实际问题和应对自然灾害的发生[1-2]。

颗粒系统可以分为准静态流、致密颗粒流和稀疏颗粒流。自巴西果效应发现以来，研究者在准静态流和稀疏颗粒流这2个方面均取得了较好的研究成果，而致密颗粒流因相互作用复杂而尚未建立起统一的解释机制。Gray[3]在关于致密颗粒流的综述中表明，目前至少有10种可解释的颗粒分离机制，包括自然渗透、对流、流态化、惯性、碰撞凝结、密度、空气阻力差、轨迹分离、聚类和有序沉降。颗粒的尺寸分离产生条件分为剪切诱导[4]和振动激励[5]。用于解释振动分离的机制无法解释剪切分离的现象，而大部分用于解释巴西果效应的机制无法解释反巴西果效应。Hong等[6]、Breu等[7]分别利用定义的颗粒温度和密度比预测反巴西果效应的发生。有学者通过实验指出，反巴西果效应依赖于间隙空气，在真空状态下不会发生；但是有其他学者模拟出了反巴西果效应，因此反巴西果效应依赖于间隙空气的说法存在争议。离散元法(DEM)的提出和计算机技术的日益成熟有助于模拟各种复杂的颗粒流[8]和工业颗粒模型，比如，类库埃特颗粒流[9]、环形剪切模型、滚筒剪切模型[10-12]、斜槽流动模型等，但是这些根据工业实际应用模拟的模型具有局限性，基于某种模型得出的结论在其他模型中并不适用。

早期通过实验观察得到的2种主流解释机制是对流和孔隙填充。Knight等[13]观察到颗粒系统在圆筒中产生对流，当颗粒与壁面的摩擦力较大时，颗粒流动方向从容器底的中部向上，再沿壁面向下，摩擦力较小时反之。Savage等[14]通过斜槽剪切流实验，提出了重力诱导、尺寸相关的空隙填充机制，以及因单个粒子上的接触力不平衡而将粒子从自身层挤压到相邻层的挤压-排出机制。对流和孔隙填充机制对颗粒流的研究具有重要的指导意义；但是这2种机制都是由宏观观察得出的结论，尚不足以揭示颗粒分离深刻的内在机理，因此模拟技术的进步有助于学者研究颗粒分离的微观机制。Jing等[15]采用DEM模拟了大、小颗粒个数均等且大颗粒在下方的二元颗粒系统，揭示了充分摩擦与旋转对促进大颗粒迁移的重要性；小颗粒在没有长期接触的情况下通过空隙进行渗透，大颗粒在剪切作用下通过具有各向异性接触网络的拥挤邻域爬升，并且受到持续剪切作用。

综上所述，在致密颗粒流方面亟需能够解释颗粒分离的新机制，为工业实际应用提供指导。采用DEM模拟分析颗粒分离的微观机制是一种很好的研究思路。Tirapelle等[16]指出，渗透实际上并不是一种基本的偏析机制，而是空间、摩擦和惯性效应综合作用的结果，空间、摩擦、惯性和阻力的结合产生了丰富的偏析现象。

本文中采用Golick等[17]、May等[18]的实验模型，在郑麟等[19-20]研究的基础上，将大、小颗粒个数均等的环形剪切薄层系统进一步改进为单一大颗粒在二元系统中的爬升模型。从空间排列结构出发，通过分析邻域小颗粒系统对大颗粒的作用，解释大颗粒上升的机理。

1 物理模型与模拟方法

环形剪切系统、颗粒层结构及大颗粒的邻域空间排列结构如图1所示。环形剪切系统由内、外圆壁面，旋转的底盘和施加正压力的顶盘构成。模拟开始前，在初始化坐标位置固定1个大颗粒，然后随机释放15 000个小颗粒自然下落，堆积在圆槽道内，弛豫一段时间，直到所有小颗粒大致稳定下来，然后在模拟时间为0.60 s时解除大颗粒的固定，盖上顶板并开始以20 s为周期旋转底盘。以圆槽底部圆心为坐标原点，建立直角坐标系，重力反方向为z轴正方向，顶盘在竖直方向上的高度可变化，底盘逆时针旋转，圆槽内径为0.588 m，外径为0.634 m，模拟的时间步长为2×10-6s，总步数为2×107，总模拟时间为40 s。在垂直方向，根据小颗粒直径将颗粒层分为5层。小颗粒在底层的排列较有序，越往上越无序。大颗粒在模拟时间为1.50 s时开始上升。

xyz—直角坐标系。(a)环形剪切系统

基于DEM，采用开源软件LIGGGHTS中的Hertz软球模型模拟环形剪切系统。Hertz软球模型中2个颗粒间的力为

F=Fn+Ft=(knαijnij-γnvn，ij)+(ktδtij-γtvt，ij)，

(1)

式中：Fn为法向力，包括弹簧力和阻尼力；Ft为切向力，包括剪切力和阻尼力；kn为法向弹性碰撞系数；αij为第i、j个颗粒的法向重叠量；nij为颗粒i球心到颗粒j球心的单位矢量；γn为法向黏弹性阻尼系数；vn，ij为第i、j个颗粒的法向相对速度；kt为切向弹性碰撞系数；δt,ij为第i、j个颗粒的切向相对位移向量；γt为切向接触的黏弹性阻尼系数；vt,ij为第i、j个颗粒的切向相对速度。

Fn与Ft必须满足摩擦屈服准则，即|Ft|≤μ|Fn|，其中|·|为向量的模运算，μ为最大静摩擦系数。kn、γn、kt、γt由颗粒材料性质决定，即

(2)

(3)

(4)

(5)

其中

式中：Y为弹性模量；R为颗粒半径；e为恢复系数；m为颗粒质量；G为剪切模量；vi、vj分别为第i、j个颗粒的泊松系数；Yi、Yj分别为第i、j个颗粒的弹性模量；Ri、Rj分别为第i、j个颗粒的半径；mi、mj分别为第i、j个颗粒的质量。

模拟中颗粒的材料性质与模拟条件参数如表1所示，其中初始化坐标y的3个数值代表3种不同的工况。

2 结果与讨论

2.1 轨迹

摩擦力越大，大颗粒上升越快，但在施加滚动摩擦阻力抑制颗粒滚动的同时，也会抑制颗粒分离的发生，可见摩擦力和滚动对大颗粒的上升十分重要。在前期工作中，已模拟了11种不同的摩擦系数与3种不同初始化位置的组合共计33种工况，其中11种摩擦系数分别为0.3、0.33、0.36、0.39、0.42、0.45、0.48、0.51、0.54、0.57、0.6，颗粒-颗粒与颗粒-壁面的摩擦系数相同；3种初始化位置分别为x=0，y=0.297 0，0.305 5，0.314 0，z=0.299 0。当摩擦系数为0.6时，初始化位置处于内壁和中间的大颗粒才能在模拟设置的时间40 s内爬升到顶部，因此选用0.6作为摩擦系数参数。

图2所示为不同初始化位置的大颗粒上升轨迹及大颗粒与壁面沿径向的相对位置。从图2(a)中可以看出，3种不同初始化位置的大颗粒上升轨迹都呈现出阶梯式的爬升现象，随着高度的增加，弛豫时间也逐渐延长，而初始化位置在中间的大颗粒首先完成了第1层的爬升。外壁的大颗粒在相同的时间内没有上升到顶部，因此大颗粒的上升与壁面有关。通过分析大颗粒相对于原点的半径轨迹，可以观察大颗粒与壁面沿径向的相对位置，如图2(b)所示。从图2(b)中可以看出，位于中间的大颗粒围绕初始化位置即图中虚线上下波动；初始位置在壁面的大颗粒始终接近壁面，位于外壁的大颗粒因离心力的作用而始终受到壁面的挤压。由此可见，大颗粒初始位置紧贴底板，最终运动到颗粒群顶部，在转盘的带动下也呈现出离心力的作用，说明环形剪切系统模型与模拟参数设置具有可行性。

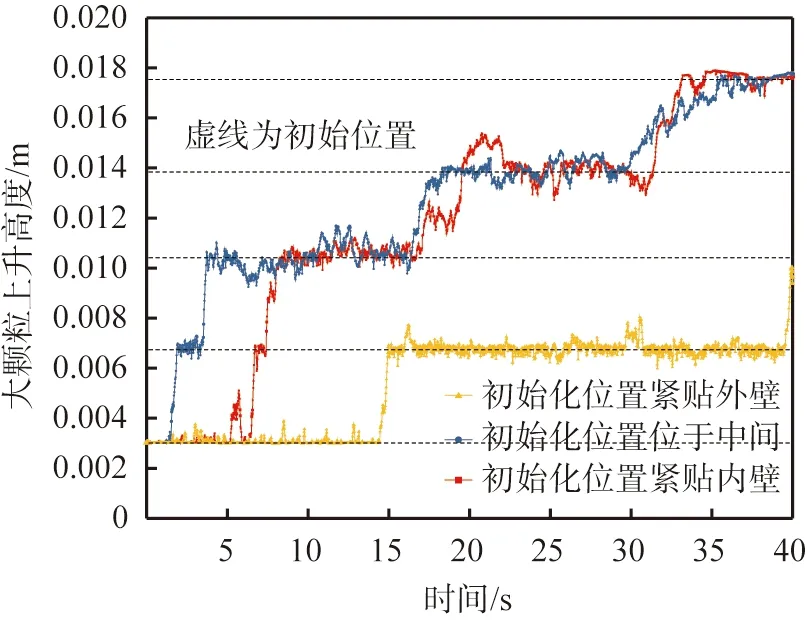
(a)大颗粒上升轨迹

2.2 速度和空间排列结构

颗粒系统由圆槽底部的底板旋转施加恒定的剪切力，再向上传递，有逐渐减小的趋势。壁面也会影响槽道内颗粒群的速度分布，处在壁面附近的颗粒很难逃离壁面运动到中间。颗粒群沿圆槽径向可分为6层颗粒，按照大颗粒初始化位置，将圆槽道颗粒系统沿径向分为5个圆环区域，以此为条件计算包含在区域内颗粒的平均速度。同理，将颗粒系统沿竖直方向分为5个小颗粒层，计算每层的平均速度。图3所示为颗粒系统中颗粒群沿水平、竖直方向的速度分布。从图3(a)中可以看出，中间的颗粒运动较快，越靠近壁面的颗粒运动越慢，壁面阻滞了附近颗粒的运动，对中间颗粒的运动影响较小。颗粒系统的动量输入来源于底板，在相邻层的传递中造成损失。从图3(b)中可以看出，第1层颗粒运动比第2层颗粒运动快3倍多，然后逐层减小；由于第1层小颗粒群的速度远大于第2层的小颗粒群的速度，因此层与层之间的动量传递依靠滑动的形式进行；大颗粒的初始化位置紧贴底板，直径是小颗粒直径的1.5倍，尺寸差异使得处于第1层的大颗粒入侵到第2层，改变了大颗粒所处位置周围的局部结构，大颗粒作为媒介，加大了周围颗粒层之间的动量传递幅度，因此在大颗粒邻域，第1层颗粒层对第2层的传递作用也是最大的。

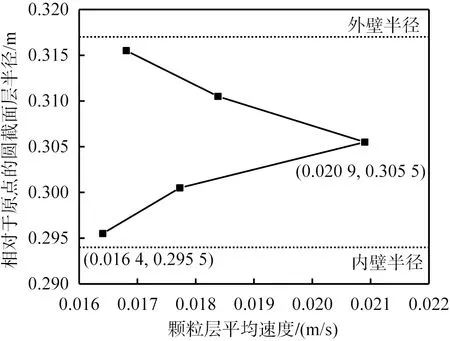
(a)水平方向

在环形剪切槽模型中，大颗粒的上升除了受摩擦力的影响，还受到壁面的直接或间接作用，另外，动量传递向上逐层减弱，大颗粒爬升越来越慢，因此选用初始化位置在圆槽中间底部的大颗粒来分析大颗粒上升到第1层的过程，从而使得到的结果更具有普适性。

在编号为1440的小颗粒持续接触条件下大颗粒上升到第1层的轨迹如图4所示。从图中可以看出，在模拟时间为1.50～1.56 s时，大颗粒经过一小段上升后进入模拟时间为1.56～1.66 s的弛豫阶段而缓慢上升，最终持续上升到第1层。在大颗粒上升到第1层小颗粒层之上的过程中，大颗粒与后方编号为1440的小颗粒持续接触，因此编号为1440的小颗粒对大颗粒的上升起到推动作用。以大颗粒质心为球心，大、小颗粒半径之和为条件半径，搜索包含在此球域的小颗粒，得到大颗粒上升过程的邻域空间排列结构演变及接触的颗粒层层数，如图5所示，其中颗粒受到来自底板的剪切力方向向右。大颗粒的上升与周围小颗粒的相对位置变化有关。从图5中可以看出，在初始化完成的0.60 s时，大颗粒主要与第2层小颗粒接触；经过一段时间的弛豫，转变为1.50 s时同时接触第1、2层的小颗粒，并开始上升过程；完成上升过程后，在1.82 s时与3层小颗粒都接触。

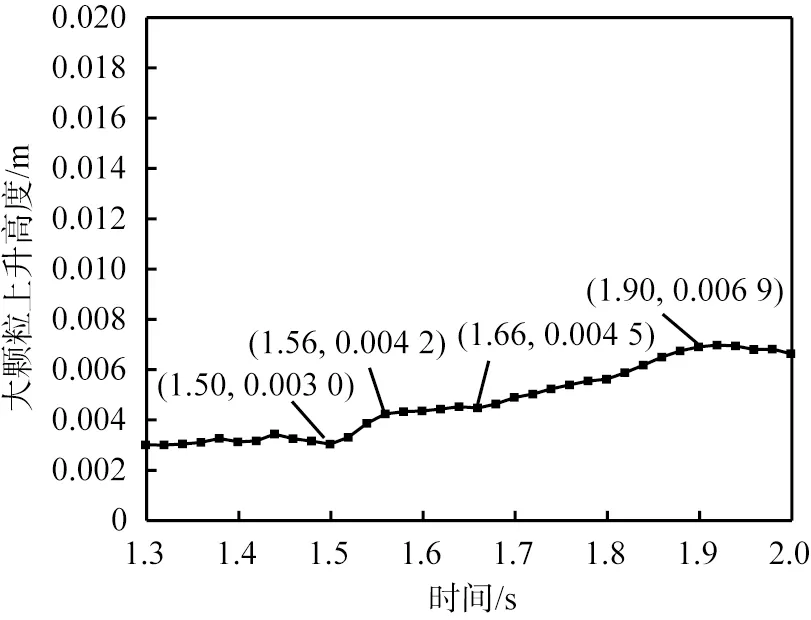
图4 在编号为1440的小颗粒持续接触条件下大颗粒上升到第1层的轨迹

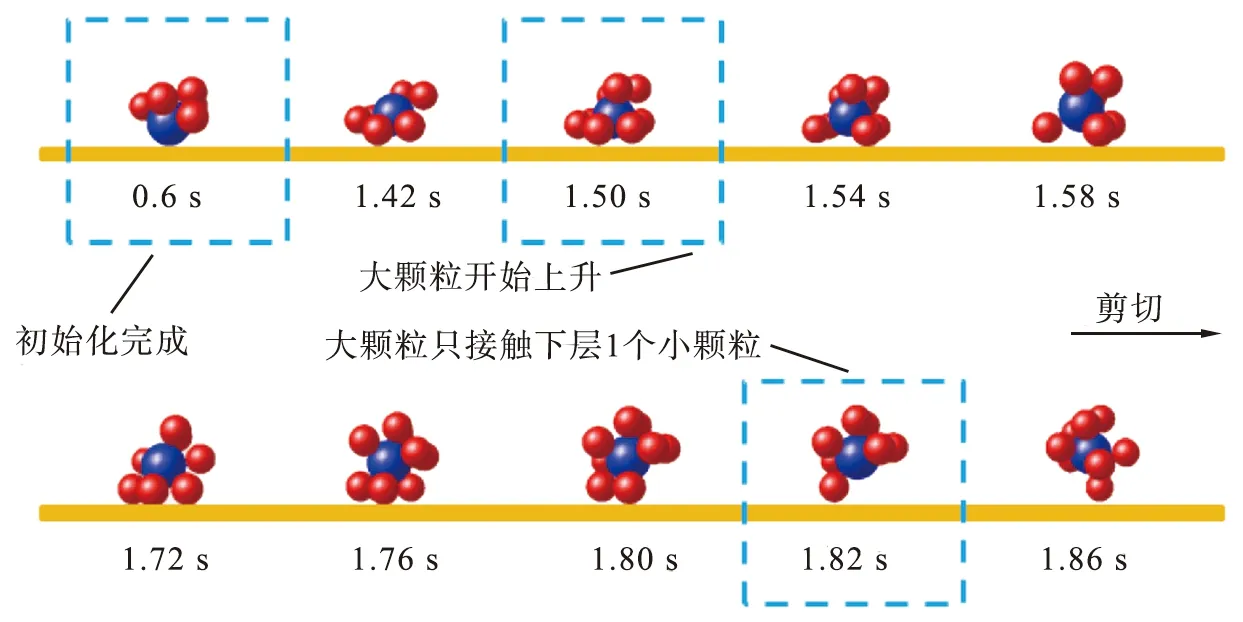
图5 大颗粒上升过程的邻域空间排列结构演变及接触的颗粒层层数

在大颗粒上升到第1层的过程中，空间排列结构的变化有3个特点：1)当大颗粒与底板接触时，底板剪切作用带动整个空间排列结构移动，发生微小变化；2)底板剪切传导和受壁面摩擦的间接作用引起的速度不同，导致空间排列结构中的个别小颗粒被替换；3)大颗粒的惯性作用使前、后接触的小颗粒不对称。

2.3 上升分析

大颗粒与底板接触时，直接受到底板的剪切作用。当大颗粒离开底板时，剪切力经第1层小颗粒传导至大颗粒，第1层5个小颗粒与大颗粒接触的个数及结构演变过程如图6所示，其中颗粒受到底板的剪切力方向向右。从图中可以看出，大颗粒在模拟时间为1.50 s时与5个小颗粒接触，随后编号为1440的小颗粒始终与大颗粒接触，另外的4个小颗粒出现间断接触，在1.80 s以后，大颗粒只与编号为1440的小颗粒接触。图7所示为大颗粒与5个小颗粒的法向重叠量变化。在软球模型中，颗粒法向重叠量大小直接反映了颗粒接触力的大小。结合图6、7可以看出，在模拟时间为1.42～1.56 s时，大颗粒受编号为0007、0249、1440、1988的4个小颗粒的挤压作用而上升；在模拟时间为1.58～1.66 s时，大颗粒主要受编号为1440、0249的前、后2个小颗粒的作用而维持高度不变；在模拟时间为1.68～1.94 s时，离心力的作用明显，大颗粒在靠近外壁面一侧编号为1440、5146、0007的3个小颗粒的共同作用下上升；在模拟时间为1.76～1.80 s时，大颗粒高度基本不变；在1.80 s以后，大颗粒在编号为1440的小颗粒的作用下上升，直到完成第1层的上升过程。

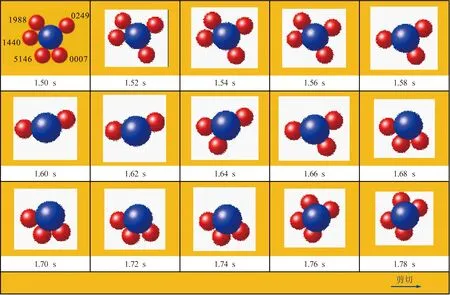
0007、1440、1988、0249、5146—模拟中5个小颗粒的编号。图6 第1层5个小颗粒与大颗粒接触的个数及结构演变过程

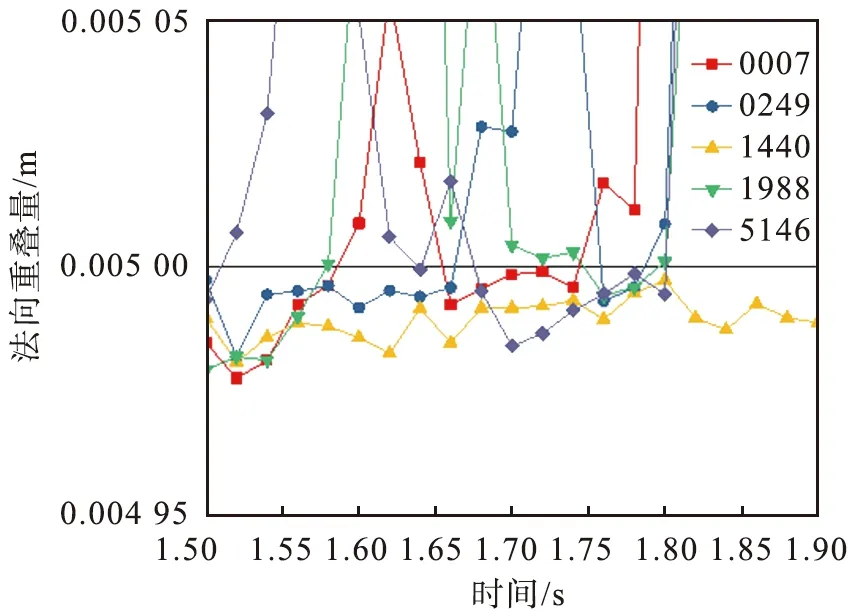
0007、1440、1988、0249、5146—小颗粒编号。图7 大颗粒与5个小颗粒的法向重叠量变化

第1层小颗粒层传递底板的剪切力是大颗粒受到的推动力和剪切力的来源，第2层小颗粒层对大颗粒主要起固定作用。在惯性作用和尺寸差异的共同影响下，大颗粒只接触下方1个后传递颗粒时的剪切力传递模式如图8所示。大颗粒在填补空隙后，受到上阻挡颗粒的阻挡，同时，受到前阻滞颗粒的阻滞，推动前方小颗粒前进。在下层，大颗粒只接触后传递颗粒，底板的剪切力通过旋转的后传递颗粒传递给大颗粒。由于大颗粒的质心高度大于小颗粒直径，因此后传递颗粒的剪切力传递模式的效果更明显。

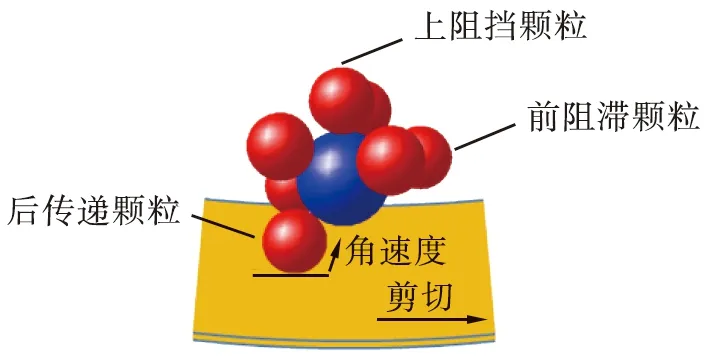
图8 大颗粒只接触下方1个后传递颗粒时的剪切力传递模式

在惯性作用下，第1层后方小颗粒推动大颗粒前进，受到第2层前方小颗粒的阻滞，因此在第2层后方出现空隙，为大颗粒的上升提供了空间条件。第2层颗粒层对大颗粒的固定作用及空隙空间的演化如图9所示，其中半透明颗粒为第1层小颗粒。从图中可以看出，在模拟时间为1.50～1.56 s时，第2层后方出现明显的空隙，对应大颗粒的第1小段上升；在模拟时间为1.56～1.66 s时，大颗粒缺少上升空间而维持高度基本不变；在模拟时间为1.68～1.80 s时，大颗粒被第2层小颗粒固定，同样缺少上升空隙，但是大颗粒的质心高度大于0.004 m，超过了小颗粒的顶点高度，经过前面时间段的弛豫，编号为1440的小颗粒对大颗粒的推动作用逐渐增强，大颗粒实现了第2小段的上升；在1.80 s以后，大颗粒只受到编号为1440的小颗粒的作用，小颗粒对大颗粒的竖直力推动明显变大，如图10所示，大颗粒完成最后的上升。

图9 第2层颗粒层对大颗粒的固定作用及空隙空间的演化

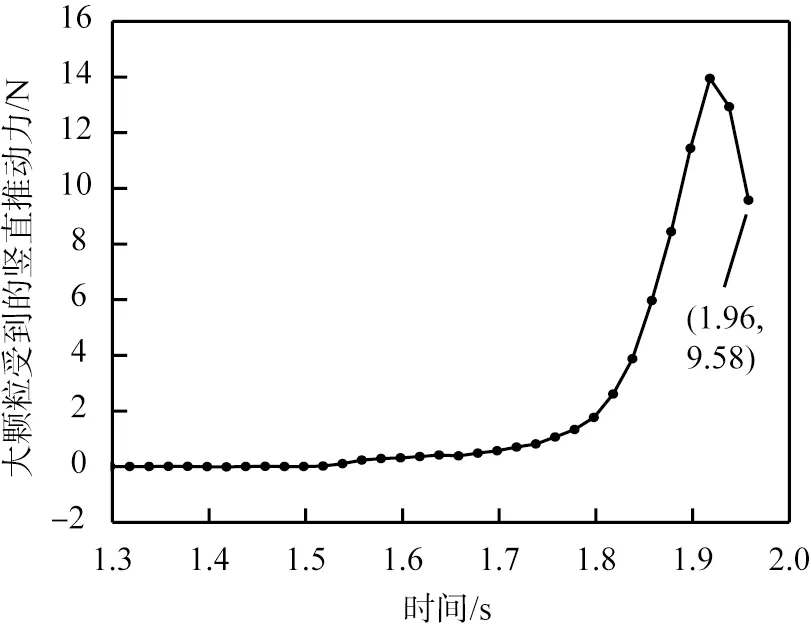
图10 编号为1440的小颗粒对大颗粒的竖直推动力

大颗粒在第2层小颗粒层的固定作用下沿接触的下方小颗粒滚动表面上升过程如图11所示。从图中可以看出，在1.80 s以后，大颗粒被固定在第2层小颗粒中，只与下层编号为1440的小颗粒接触。小颗粒在底板剪切作用下前进，大颗粒则保持位置基本不变，因此大颗粒是沿着滚动的小颗粒表面升高的。

3 结论

本文中基于DEM，采用开源软件LIGGGHTS，针对环形剪切流颗粒系统，研究了单一大颗粒在小颗粒群系统中分离的作用机理，探讨了摩擦力大小、壁面、尺寸差异、惯性等因素对大颗粒空间排列结构的影响，得到如下结论：

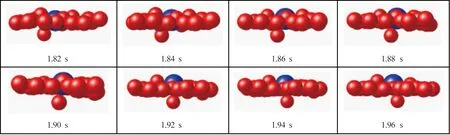
图11 大颗粒在第2层小颗粒层的固定作用下沿接触的下方小颗粒滚动表面上升过程

1)大颗粒轨迹呈现阶梯状爬升的过程，尺寸差异是大颗粒能够沿着小颗粒群向上爬升的根本条件，大颗粒在上升过程中受到某接触小颗粒的持续作用，并沿着此小颗粒表面上升，因此呈阶梯状向上爬升。

2)大颗粒受到空间条件、力学条件2种机制的共同作用而上升。①空间条件。颗粒群的运动速度在竖直方向呈非线性分布，底层颗粒的平均速度是第2层大颗粒速度的3倍多，动量在由下到上的传递过程中发生损耗。大颗粒的尺寸效应体现在对前上方小颗粒动量传递模式的改变。大颗粒的尺寸入侵改变了前方上层小颗粒间的动量传递模式，直接正面挤压使得前方小颗粒具有与大颗粒相同的速度，而大颗粒后方的小颗粒以该层平均速度运动，因此在大颗粒后方出现空隙，成为大颗粒上升的通道。②力学条件。大颗粒的差异入侵引起小颗粒群的排斥，小颗粒群对小颗粒顶点高度范围内的大颗粒持续挤压，空间条件的产生是该阶段大颗粒上升的充分条件。当大颗粒只接触后下方1个后传递颗粒时，形成单一小颗粒提供传动的模式，大颗粒作为从动颗粒沿着后传递颗粒表面上升。