例举从不同角度解决立体几何动点问题的策略

吴文娟 张 辉(特级教师)

(北京市陈经纶中学)

立体几何中的动点问题是一类常见问题,解决此类问题通常有两种方法:一是几何法,主要是通过作图,利用定理进行推断、证明和计算,常常会用到反证法,借助极端位置、特殊位置加以分析;二是空间向量法,建立空间直角坐标系、设点,通过坐标运算得出结论.如果问题不需要定量计算,首选几何法.如果需要计算,可以先考虑运用几何法分析出几何性质,然后计算;如果比较容易建立空间直角坐标系或变量较多、不易直接找出所需要的位置关系,可以首先考虑向量法.下面通过具体例题加以说明.

例1如图1 所示,在长方体ABCD-A1B1C1D1中,AB＝AD＝2,AA1＝1,O是AC的中点,点P在线段A1C1上.若直线OP与平面ACD1所成的角为θ,则cosθ的取值范围是( ).

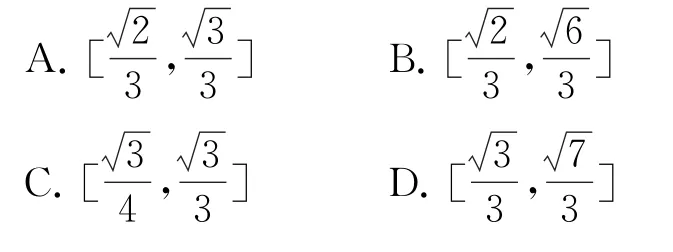
图1

解析方法1本题是一道选择题,需要运算求解cosθ,因此可以采用几何法分析图形的几何性质,通过极端位置分析求解.

图2

方法2此题可以建立空间直角坐标系,利用向量法求出sinθ,进而求出cosθ.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系(如图3),则A(2,0,0),C(0,2,0),O(1,1,0),D1(0,0,1).

图3

点评解选择题可以先研究特殊位置,再研究一般位置,归纳位置关系后直接利用极端位置加以分析.如果想避免复杂的分析与推理,或不能准确判断空间位置关系,就可以直接运用空间向量坐标运算.由于涉及范围,所以最终都要用到函数求最值的方法.方法2采用了二次函数求最值的方法,求解时需要注意自变量的取值范围,此题选用特殊位置的方法求解会比较快捷.

例2如图4所示,在直三棱柱ABC-A1B1C1中,若BC＝2AB＝2,AA1＝AC＝,M是B1C1的中点,过AM作这个三棱柱的截面,当截面与平面ABC夹角最小时,这个截面的面积为( ).

图4

解析方法1本题主要考查无棱二面角的最值问题,解题的关键在于寻找截面ANME(如图5).过点M作底面ABC的垂线,垂足为BC的中点D,根据定义作出二面角的平面角.要想使二面角最小,只需使垂足D到过点A的棱的距离最大.二面角的棱为底面ABC内过点A的直线,显然最大距离为AD,即过点A作AD的垂线,该垂线为二面角的棱时,二面角最小.通过找到截面与棱的交点的位置,来确定截面图形,进而求出截面面积.具体做法如下.

图5

取BC的中点为D,连接MD,因为M为B1C1的中点,所以B1M∥BD且B1M＝BD,所以B1B∥MD.因为B1B⊥平面ABC,所以MD⊥平面ABC.过点D作AD的垂线交AC于点F(如图6),因为在直三棱柱ABC-A1B1C1中,BC＝2AB＝2,AA1＝AC＝,M是B1C1中点,易得FD＝FC＝,故点F为AC上距C较近的三等分点.取A1C1上距C1较近的三等分点为点E,在平面A1B1C1内,延长EM交A1B1的延长线于点G(如图7),得B1G＝A1B1,即B1为线段A1G的中点,连接AG交B1B于点N,易知N为B1B的中点,故截面与平面ABC夹角最小时的截面即为四边形ANME.

图6

图7

方法2建立空间直角坐标系,采用向量法将截面与平面ABC的夹角θ满足的余弦函数关系用坐标表示出来,从函数角度寻找函数值取得最大值时自变量的取值,所以需要把截面与直线BB1和A1C1的交点坐标求出来,再根据四边形的面积求解即可.

图8

点评本题考查无棱二面角最值问题,对于空间想象力要求较高.采用几何法需要作出二面角的平面角,将空间问题平面化进行运算求解,找到二面角后,用平面几何的方法就能比较容易得出答案.采用向量法入手容易,难点是对cosθ＝|cos〈m,n〉|＝进行处理,即采用整体换元的方法将“三元”合理转化为“一元”求解,但是能想到这一步确实存在一定的难度,需要明确代数式子的变形方法及方向.

例3如图9 所示,等腰直角△ABC中,AC＝BC＝2,点P为平面ABC外一动点,满足PB＝AB,∠PBA＝,给出下列四个结论:

图9

①存在点P,使得平面PAC⊥平面PBC;

②存在点P,使得平面PAC⊥平面PAB;

③设△PAC的面积为S,则S的取值范围是(0,4];

④设平面APB与平面PBC夹角的大小为θ,则θ的取值范围是其中正确的结论是( ).

A.①③B.①④ C.②③D.②④

解析方法1此题①②两个结论是位置关系的判定,③④两个结论是几何量取值范围的求解.可以先采用几何法,依据定理判断①②是“存在”问题,所以可以考虑极端位置和特殊位置,也可以用反证法处理.

对于①,如图10 所示,当PB⊥BC时,因为PB⊥AB,BC∩AB＝B,所以PB⊥平面ABC,则PB⊥AC.又AC⊥BC,PB∩BC＝B,所以AC⊥平面PBC,又AC⊂平面PAC,所以平面PAC⊥平面PBC,故①正确.

图10

对于②,取AP的中点M,连接BM,CM,因为PB＝AB,所以MB⊥AP.假设平面PAC⊥平面PAB,则MB⊥平面PAC,MB⊥CM,而BM＝BC＝2,所以∠BMC＝∠BCM＝90°,与三角形内角和定理矛盾,不成立,故②错误.

对 于③,因 为AP＝4,AC＝2,所 以S△PAC＝AP·AC·sin∠PAC＝4sin∠PAC.由点P在平面ABC上的极限位置判断可知,当点P在平面ABC内,且C,P在A,B的异侧,则∠PAC＝90°;当C,P在A,B的同侧时,A,C,P共线,则∠PAC＝0°,因为点P在平面ABC外,则S的取值范围是(0,4),故③错误.

对于④,因为∠ABC＝45°,当点P在平面ABC内时,θ＝0,当点P运动时,点P是绕AB轴旋转,因此可以找极限位置求解.设点A到平面PBC的距离为h,因为PB⊥AB,所以sinθ＝,所以,当且仅当PB⊥平面ABC时,等号成立,所以θ的取值范围是,故④正确.

综上,选B.

方法2分别以CA,CB所在直线为x轴、y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系(如图11).

图11

点评这道题采用几何方法更易判断,反证法可以证明不存在,极端位置可以将变量的范围加以限定.采用向量法判断③④时与例1和例2类似,最后得出函数关系式,转化为已知变量范围求函数的值域问题,求解时经常会用到消元、换元等方法.

例4在棱长为1的正方体ABCD-A1B1C1D1(如图12)中,M,N分别为BD1,B1C1的中点,点P在正方体的表面上运动,且满足MP⊥CN,则下列说法正确的是( ).

图12

A.点P可以是棱BB1的中点

B.线段MP的最大值为

C.点P的轨迹是正方形

D.点P轨迹的长度为

解析方法1用几何法先定性分析,再定量计算,从特殊到一般进行解题.

过M作MQ∥AB交平面BCC1B1于点Q,则点Q为正方形BCC1B1的中心,在平面BCC1B1内过点Q作FG⊥CN分别交BB1,CC1于F,G两点,再过F作FE∥AB交AA1于点E,作GH∥CD交DD1于点H.连接点E,H,易知E,F,G,H共面且该平面过点M(如图13).由AB⊥平面BCC1B1可证CN⊥平面EFGH,则P的轨迹为四边形EFGH的边界.显然四边形EFGH是矩形,且EF＝1,FG＝,周长为2＋,M为矩形EFGH对角线的交点,线段MP的最大值为,故选D.

图13

方法2在正方体ABCD-A1B1C1D1中,以点D为坐标原点,分别以DA,DC,DD1方向为x轴、y轴、z轴正方向,建立空间直角坐标系(如图14).因为该正方体的棱长为1,M,N分别为BD1,B1C1的中点,所以1),C(0,1,0),故.设P(x,y,z),则

图14

解析方法1 通过分析特殊位置得出CN⊥平面EFGH,进而得到动点P的轨迹.方法2 则采用坐标法,通过运算得出相关点的位置,避免了对几何体中复杂位置关系的判断,是一种能较快判断位置关系的方法.

例5已知正方体ABCD-A1B1C1D1(如图15)的棱长为2,E,F分别是棱BC,CC1的中点,动点P在正方形BCC1B1(包括边界)内运动,若PA1∥平面AEF,则线段PA1的长度范围是( ).

图15

解析方法1根据题意,连接D1F,AD1,取BB1的中点G,B1C1的中点H,连接A1H,A1G,GH,找到过A1与平面AEF平行的平面,从而得到A1P所在的平面(如图16),进而借助面面平行探求线面平行.

图16

在正方体ABCD-A1B1C1D1中,A1G∥D1F,A1H∥AE,EF∥AD1,所以A,E,F,D1共面.因为A1G⊄平 面AEFD1,D1F⊂平面AEFD1,所 以A1G∥平面AEFD1.同理可得A1H∥平面AEFD1.

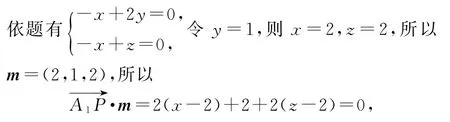
图17

点评寻找动点的轨迹可以通过几何体表面的轮廓线作出平行平面,找到平面与平面的交线,从而找到动点的运动轨迹;也可以选择用向量法进行“以算代想”,找到动点运动的轨迹.

总之,运用几何法解题,需要具有一定的空间想象能力,能够在几何体中找出基本元素之间的关系,进而在解决问题的过程中抓住特殊位置进行分析,其中寻找运动过程中的不变量往往是解决问题的关键.运用向量法解决动点问题可以避免较为复杂的作图和推理,将动点问题转化为函数在给定范围内的值域或是方程是否有解等问题,很好地体现了形与数的结合,以及运用代数法解决几何问题的优势.两种方法各有所长,几何法多是“少算多想”,向量法则多是“少想多算”,将两种方法较好地融合,可以更好地促进空间想象能力和数学运算素养的提升.

(完)