高中数学空间图形截面问题的解题策略研究

方 凤

(广东省鹤山市第一中学)

在立体几何中,截面是指用一个平面去截一个几何体得到的平面图形.空间图形截面问题是高考的热点和难点,主要考查判断截面的形状和计算相关问题.要想顺利地解决这些问题,首先要掌握如何作空间图形的截面.

1 空间图形截面作图的主要原理

1)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内;

2)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线;

3)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;

4)如果两个平面平行,第三个平面和它们相交,那么两条交线平行.

2 空间图形截面作图主要方法

作空间图形的截面,需要较强的空间想象能力和逻辑推理能力,对学生来说是一个难点.要想找到空间图形截面的形状,就要弄清这个平面与空间几何体的各个面交线的位置和形状.掌握作截面图的方法,深入理解直线和平面的有关性质,能够有效地突破与截面相关的问题.

例1在正方体ABCD-A1B1C1D1中,P为BB1的中点,画出过点A1,D1,P的截面.

解析连接共面的两点A1,P,由于A1,D1,P在一个平面内,且平面A1ADD1和BCC1B1平行,只要过P作A1D1的平行线即可.设CC1的中点为Q,连接PQ和D1Q,于是得到截面A1D1QP,如图1所示.

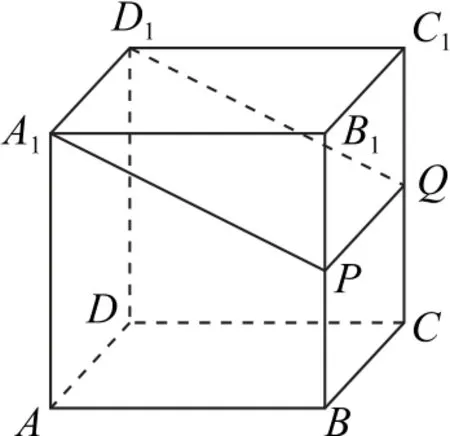
图1

例2如图2所示,在正方体ABCD-A1B1C1D1中,E,F,G分别在AB,BC,DD1上,画出过点E,F,G的截面.

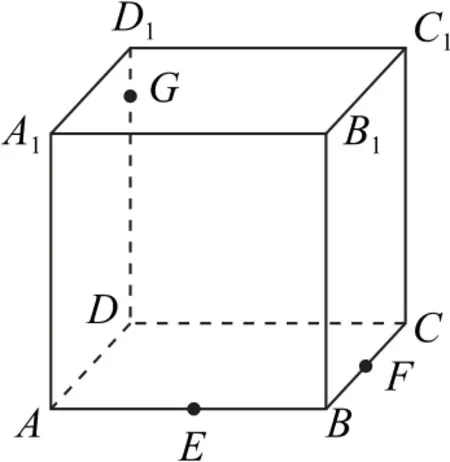
图2

解析在底面ABCD内,过E,F作直线EF,分别与DA,DC的延长线交于L,M;在侧面A1ADD1内,连接LG交AA1于K;在侧面D1DCC1内,连接GM交CC1于H;连接KE,FH,则五边形EFHGK即为所求的截面,如图3所示.

图3

例3如图4 所示,已知长方体ABCDA1B1C1D1中,E为平面A1B1C1D1内一点,K为底面ABCD内一点,F为侧面AA1B1B内一点,画出过点E,F,K的截面.

图4

解析过F作OF∥BB1,交AB于O,交A1B1于S;连接OK并延长交BC于U,作UT∥BB1,交B1C1于T;再连接TS,KF,并延长相交于X,交TU的延长线于V;再连接XE交A1D1于P,并延长交D1C1于N,交B1C1的延长线于Y;再连接YV,交CC1于M,交BC于H;再连接HK并延长交AB于G;再连接GF并延长交AA1于Q,再连接PQ,MN,就得到所求截面PQGHMN,如图5所示.

图5

3 空间几何体截面的有关计算

空间几何体的计算要掌握好“定位”“定形”“定量”这三个重要的环节.首先,确定出关键点;其次,由关键点确定截面与空间几何体的交线;再次,根据题中已知条件以及空间点、线、面的位置关系确定截面的基本特征和形状;最后运用平面几何的有关知识解决问题.

例4如图6 所示,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为AA1,AB的中点,M是正方形ABB1A1内的动点,若C1M与平面CD1E平行,则点M的轨迹长度为________.

图6

解析如图7所示,设A1B1的中点H,BB1的中点G,连接GH,C1H,C1G,EG,HF,可得四边形EGC1D1是平行四边形,所以C1G∥D1E,又C1G⊄平面CD1E,D1E⊂平面CD1E,所以C1G∥平面CD1E.同理可得C1H∥CF,C1H∥平面CD1E,又C1H∩C1G＝C1,所以平面C1GH∥平面CD1E.

图7

因为点M是正方形ABB1A1内的动点,C1M∥平面CD1E,所以点M在线段GH上,故点M的轨迹长度为GH＝

例5在三棱锥P-ABC中,PA,PB,PC两两垂直,PA＝3,PB＝4,PC＝5,点E为线段PC的中点,过点E作该三棱锥外接球的截面,则所得截面圆的面积不可能为( ).

A.6π B.8π C.10π D.12π

(完)