二次函数增减性性质新说及其应用
⦿福建省武夷山市第二中学 林梦雨
1 引言
增减性是抛物线的一条非常重要的性质,也是重要的考点,下面就对性质及其应用归纳如下,仅供学习时借鉴.
2 引理

(1)当a>0时,若d1>d2,则y1>y2;
(2)当a<0时,若d1>d2,则y1 下面以a>0为例加以证明. 证明:如图1. 图1 综上所述,当a>0时,若d1>d2,则y1>y2成立. A.2 B.3 C.4 D.5 由a>0,得c<0,则abc<0,故①正确. 所以正确的个数有5个.故选:D. 点评:本题考查了二次函数的图象与系数的关系、二次函数的最值、二次函数与x轴的交点情况、二次函数与一元二次方程之间的关系、二次函数的性质等知识点,综合性较强,需灵活运用二次函数的以上相关知识点. 图2 由抛物线y=ax2-2ax+c过点A,可得c=1. 为了进一步检验经过响应面设计试验所获得的模型及其预测的最佳工艺条件的可靠性,在最佳工艺条件进行验证试验,并重复5次,结果及统计分析如表6所示:对于酵母固态发酵551H及552H,验证试验结果与预测结果差异性均不显著(P>0.05),因此,模型预测的最佳工艺参数适合实际应用。 点评:解答时,有三点需要把握好.一是用好配方法确定抛物线的对称轴;二是用好“ady”法则计算距离d并准确比较大小;三是灵活运用分类思想,结合“ady”法则计算即可. 例3(2021·日照)抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,其图象如图3所示.下列结论:①abc<0;②(4a+c)2<(2b)2;③若(x1,y1)和(x2,y2)是抛物线上的两点,则|x1+1|>|x2+1|时,y1 图3 A.4 B.3 C.2 D.1 解析:由抛物线图象开口向上,可得a>0.又对称轴在y轴左侧,所以a,b同号,即b>0. 由抛物线与y轴交点在x轴下方,得c<0.所以abc<0,故①正确. (4a+c)2-(2b)2=(4a+c+2b)(4a+c-2b),当x=2时ax2+bx+c=4a+c+2b,由图象可得4a+c+2b>0,当x=-2时,ax2+bx+c=4a+c-2b,由图象可得4a+c-2b<0,所以(4a+c)2-(2b)2<0即(4a+c)2<(2b)2.故②正确. 因为抛物线的顶点坐标为(-1,m)且a>0,所以y≥m,即ax2+bx+c≥m,即抛物线与直线y=m有交点,而m-1位于直线y=m下方,故抛物线与直线y=m-1无交点,方程ax2+bx+c=m-1无实数根.故④正确. 综上所述,①②④正确.故选:B. 点评:解答时,有两个关键点要把握好.一是“ady”法则的理解和运用,这可以准确判断结论③;二是灵活运用函数的最小值以及数形结合思想判断方程的根,这一点也是很重要的. 例4已知二次函数y=ax2-3ax+c(a<0)的图象上有三个点(-1,y1),(2,y2),(3,y3),则y1,y2,y3的大小关系是( ). A.y2 C.y1 故选:D. 点评:解答时,准确计算抛物线的对称轴以及点的横坐标与对称轴的距离是解答的基础性条件,熟练掌握“ady”法则是解题的关键. 二次函数是初中数学的重要内容,熟练掌握其性质更是学习的重点之一,特别是增减性尤其重要.为此,要做到如下三点. (1)掌握增减性的基本描述方式,这是掌握性质的基础,也是性质变形的根本依据. (2)灵活掌握创新的“ady法则”,法则与原性质对比有两大优点:一是不需要判断点与对称轴的位置关系,不需要分其在对称轴的左侧还是右侧,避免了解答时易出现的错误;二是解决了二次函数图象上所有的点的函数值的大小比较问题,提高了解题效率. (3)通过性质的运用,数形结合思想、分类思想、绝对值思想都得到了充分的展示和应用,这也是解题时必须要牢记的.


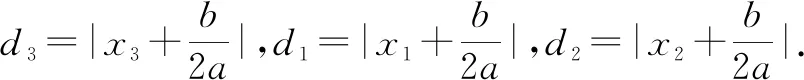
3 引理运用
3.1 判断最小值是否正确
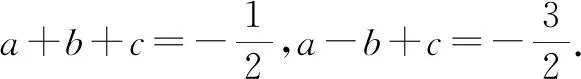
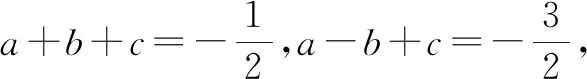
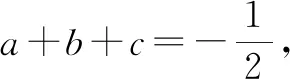


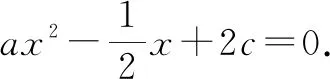
3.2 根据最大值计算参数值


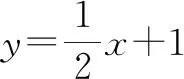

3.3 判断结论的正误

3.4 比较函数值的大小
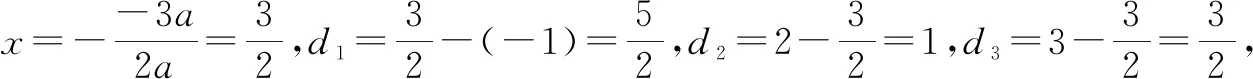
4 解后反思

