通过一题多解 培养关键能力*

⦿福建省泉州师范学院附属中学 庄惠强

1 引言

教育部于2022年4月颁布的《义务教育数学课程标准(2022年版)》(以下简称《新课标》)指出：初中数学核心素养的主要表现包括运算能力、几何直观与空间观念等.运算能力方面要求学生能选择合理简洁的运算策略解决问题,通过运算促进数学推理能力的发展[1].

“关键能力”指的是学生在运用知识解决问题的过程中所需要的主要学科能力,包括逻辑推理能力、运算求解能力、直观想象能力、数学建模能力和创新能力五个方面[2].在培养五大关键能力的过程中,针对不同的素材,教师要有所侧重.本文中结合一题多解案例,阐述如何培养学生运算求解能力.

2 通过一题多解培养学生关键能力的案例解析

2.1 案例呈现

如图1,已知AB=8,点P是线段AB上的一个动点,分别以AP，BP为边,在线段AB的同侧作菱形APCD和菱形PBFE,点P,C,E在同一条直线上,∠DAP=60°,M，N分别是对角线AC，BE的中点,当点P在线段AB上移动时,求点M，N之间距离的最小值.

图1

2.2 培养学生关键能力的解析

2.2.1 提升整体思维,培养学生用数学眼光观察世界 教师要时时刻刻、事事处处站在系统的高度讲授知识,让知识总是以“系统中的知识”的面目出现在学生面前[3].

教师要提升学生的整体思维,概括解题的一般方法,帮助学生积累基本活动经验.当学生具备解题的基本活动经验,就能高屋建瓴、整体把握主要矛盾,用数学的眼光观察问题.初中阶段,与计算线段长度或角的度数相关的的通性通法如图2所示，包括四种情况.

图2

通过数学的眼光,可以从现实世界的客观现象中发现数量关系与空间形式, 提出有意义的数学问题；能够抽象出数学的研究对象及其属性,形成概念、关系与结构；形成对数学的好奇心与想象力,主动参与数学探究活动, 发展创新意识[1].

本案例中,线段MN是一条独立的线段,要计算它的长度,通性方法没有用武之地.从整体眼光来看,把线段MN“置于三角形中”,就能运用以上四种方法计算,因此把眼光重点放在如何构造三角形上.这种结构化思维,能帮助学生拨去迷雾,理清思路.

2.2.2 揭示思维过程,培养学生用数学思维思考世界 在义务教育阶段,数学思维主要表现为运算能力、推理意识或推理能力.数学的思维体现为能根据已知事实或原理,合乎逻辑地推出结论,构建数学的逻辑体系；能够运用符号运算、形式推理等数学方法,分析、解决数学问题和实际问题[1].

(1)加强通性意识,揭示思维过程

因为直角三角形的角与角、边与边、边与角的关系非常稳固,方便计算边的长度或角的大小,所以首选构造直角三角形.

解法一：如图3,分别过点M，N作MG⊥AB，NH⊥AB,垂足为G，H,过点M作MI⊥NH于点I.

图3

在Rt△MIN中,因为∠MIN=90°,且

所以，可得

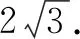
这种思维完全符合学生的认知水平,符合学生的“最近发展区”,学生容易接受、易于找到思维的入口,从“独立”到“联系”，化“未知”为“已知”.把线段的长度“置于三角形中”计算,这种思维增强了学生的整体意识,教会学生结构化思维.

(2)梳理解法联系,尊重思维差异

教师要着眼于知识间的联系和规律,使学生从系统的高度去把握知识,进行思考,做到八方联系,浑然一体[3].

解法一是通性通法,优点是容易“切题”,缺点是要作三条辅助线、结构复杂、计算量大.留给学生充足的时间,让学生展开讨论交流,学生的思维差异就会显现出来.

如图4,连结MP，NP.因为∠APC+∠BPE=180°,又易得MP是∠APC的角平分线,NP是∠BPE的角平分线,所以∠MPN=90°,即△MPN是直角三角形.与解法一相比,虽然都是构造直角三角形,但是用这种方法构造的直角三角形,图形简洁,结构简单,计算容易,其优越性不言而喻.善于发现并挖掘图形的特殊特征,是学生学会“数学的思维”的体现,通过计算将已知条件约简,把条件向前推进一大步,经历数学“再发现”的过程,发展学生的批判性思维.

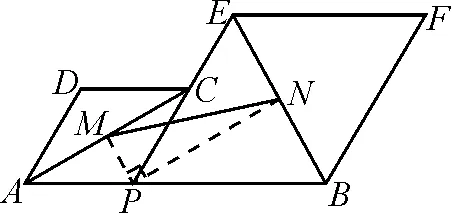
图4

解法二：如图4，连结MP，NP,则PM⊥AC，PN⊥BE.

所以，在Rt△MPN中,由∠MPN=90°,可得

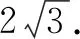
挖掘图形的特征,找出题目的“个性”,推导出更进一步的结论,为后续的运算求解打下基础.要尊重学生的思维差异,对于有奇思妙想的学生要给予充分的肯定,对于常规思维的学生,也要给予鼓励,肯定他们思维的价值,培养他们的学习信心.

2.2.3 领悟数学模型,培养学生用数学语言表达世界 初中阶段,数学语言主要表现为模型意识、模型观念和应用意识.引导学生构造三角形的中位线模型,让学生从通性通法转化到数学模型.

根据布鲁姆认知理论,回忆、理解与应用属于低阶思维,分析、评价与创造属于高阶思维.本案例中点M，N分别是两条线段的中点,让人自然联想到构造数学模型——三角形的中位线.但是线段MN却不在一个三角形中,没办法直接利用三角形中位线的性质解题.连结PD，PF,根据菱形的性质,对角线的中点也是对角线的交点,构造△PDF,则线段MN是△PDF的中位线,这种思维属于高阶思维的范畴.

如图5,连结PD，PF.因为M，N分别是对角线AC，BE的中点,所以点P，M，D三点共线,点P，N，F三点共线.

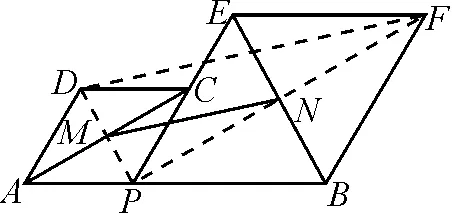
图5

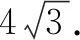
空间观念有助于理解物体的形态与结构,根据物体之间的位置关系,感知并描述图形的运动和变化规律.几何直观体现在能根据图形的特征,数形结合构建直观模型,把握问题的本质,明晰思维的路径[1].

3 一题多解培养学生关键能力的策略

培养学生的关键能力，鼓励多种解法,发展思维的流畅性；链接不同解法,启发思维的灵活性；鼓励自创解法,促进思维的独特性[4].基本策略概括如下.

(1)注重提升整体观念,让学生拥有数学的眼光

解题教学应该强调通性通法,找出具有相同性质题目解法的“最大公因数”,即寻找解题的“共性”,让学生解题时有“法”可依、有“章”可循.通过解题提升学生的整体观念,帮助学生总结运算求解过程中常用的方法,帮助学生寻找解题的一般路径.解题过程貌似只是考查个别题目的解法,实则是考验学生对知识的总体把握.厘清概念,准确运用运算法则,迅速找到解题方向、理清解题思路,熟练应用解题技巧,让学生拥有数学的眼光.

(2)注重把握特殊性质,让学生拥有数学的思维

林崇德先生认为：思维品质包括敏捷性、灵活性、创造性、批判性与深刻性[5].在强调通性通法的同时,也应该培养学生准确捕捉信息的能力,如代数式之间的联系、几何图形中隐含特殊的性质,都可能为解题提供良好的切入点,让学生从“有联系的程序”入手,发展到“做数学”.这是一个从“共性”的总体指导,到寻找题目“个性”的过程,在这个过程中,主要就是引导学生“有逻辑地思考”,培养良好的思维品质,从而让学生拥有数学的思维.

(3)注重数学思想指导,让学生拥有数学的语言

数学的解题,离不开数学思想的指引,方程思想、函数思想、模型思想、数形结合思想等能让学生拥有科学的指导思想.如，数形结合是学生解题最重要的方法之一,“数缺形时少直观,形缺数时难入微”,数形结合,能够让学生实现图形语言、符号语言与数学语言的熟练切换.模型思想,能让学生建构独特的知识体系,让学生更好地解题.因此，应培养学生的模型思想、应用意识,让学生拥有数学的语言.

4 结束语

解题教学与知识教学不同,主要按运用已有的知识体系解决问题的数学范式进行[6].这种范式要求学生有大局观，能把握“共性”,又要细致入微把握事物的“个性”,在数学思想的指导下进行发散性思维,在基本活动经验的帮助下提高解决问题的能力.

教学的本质就是教会学生学会思维.通过一题多解,教师讲课可以做到“少而精”,学生练习“时间足、手段广”,在提高学生运算求解能力的同时,也会带动逻辑推理能力、直观想象能力、数学建模能力与创新能力的提高,从而全面培养学生的数学关键能力.