集中荷载下固定铰支剪式可展桥梁结构分析与参数优化
徐伟炜
(东南大学土木工程学院,南京 210096)(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
在应急救援期内,交通系统承担着重要运输任务,必须全力抢通.传统应急装备采用桁架片拼装成结构,但零部件多,单件质量大,无法整体投送,严重影响装备机动性能[1].标准剪式单元是由2根两端及中间开孔的剪叉杆件经销轴连接中间销孔构成的一种X形机构,具有单元模块化、长度变化灵活等特点[2].近年来,国内外相继发明了多种剪式可展桥梁[3-13].广岛大学试制了人行桥和车行桥模型[8-9].
从剪式结构研究现状来看,大部分局限于对特定可展结构进行仿真分析或试验研究,鲜有综合考虑构型参数和冗余约束对剪式结构性能影响及其机理、调控方面的研究.因外荷载作用下不同约束条件剪式结构内力可以看作是外荷载作用下两端固定铰支剪式结构和端部水平反力作用下约束剪式结构两部分内力的叠加,故集中荷载作用下两端固定铰支剪式结构分析与参数优化是剪式桥梁结构设计的关键问题之一.
针对强度约束下剪式结构最轻质量设计,本文建立了集中荷载作用下两端固定铰支座剪式结构的一般力学模型,推导了各剪叉杆内力及杆件最大应力,结合定义的剪式结构质量影响系数,获得剪叉杆件水平夹角与标准单元数、剪叉杆件形状系数之间的最优关系,为剪式可展桥梁结构方案设计提供参考.
1 组成及力学分析
两端固定铰支座剪式结构由左支座处半单元、中间m个标准单元和右支座处半单元组成,剪叉杆之间通过销轴铰接,并根据铰接的位置分为上销、中销和下销(见图1).图中,O1、O2分别为左、右支座;Aj、Bj、Cj分别为第j(j=0,1,2,…,m)个上、中、下销点;S为剪叉杆长度;θ为剪叉杆与水平方向的夹角;L、H分别为剪式结构的跨度和高度.

图1 两端固定铰支座剪式结构示意图
由几何关系可得
L=(m+1)Scosθ
H=Ssinθ
(1)
1.1 支座反力
设剪式结构的第j个上销点上作用有可移动集中荷载Pj,则在左、右支座处将引起水平方向反力FO1x、FO2x和垂直方向反力FO1y、FO2y(见图2).

图2 支座受力示意图
由虚位移原理可得
则
(2)
对O2支点取矩可得
则
(3)
由∑Fx=∑Fy=0可得
1.2 上、下销内力
将O1支座至第i个标准单元组成的剪式机构取为隔离体.在第j个上销点的集中荷载Pj作用下,上销点Ai处将引起销点水平方向内力FAi x和垂直方向内力FAi y,下销点Ci处将引起销点水平方向内力FCi x和垂直方向内力FCi y(见图3).

(a) 无移动荷载
当剪式机构隔离体上无移动荷载时,对Ci点取矩可得
则
(4)
对Ai点取矩可得
则
(5)
由∑Fy=0可得
FAi y+FCi y+FO1y=0
(6)
由虚位移原理可得
即
FAi y-FCi y=-(1+2i)tanθFO1x
(7)
联立式(6)和(7),得
(8)
(9)
当剪式机构隔离体上存在移动荷载时,对Ci点取矩可得

则
Pj(i-j)cotθ
(10)
对Ai点取矩可得
则
(11)
由∑Fy=0,得
FAi y+FCi y+FO1y-Pj=0
(12)
由虚位移原理可得

即
FAi y-FCi y=Pj-(1+2i)tanθFO1x
(13)
联立式(12)和(13),得
(14)
(15)
1.3 杆件内力
按照杆件的相对位置,可将剪叉杆件分成杆件AiBi、杆件AiBi+1、杆件CiBi和杆件CiBi+1四类.令NAiBi、QAiBi、MAiBi分别为杆件AiBi在点Bi横截面处的轴力、剪力和弯矩,其中轴力以受拉为正,剪力和弯矩以逆时针为正.其他3类杆件内力的设定与杆件AiBi相同.
1.3.1 杆件AiBi内力
取杆件AiBi为隔离体,则
(16)
当0≤i≤j时,将式(1)、(2)、(3)、(4)、(8)代入式(16)可得

(17)
由式(17)可知,NAiBi为i的线性函数且恒为负,故|NAiBi|在i=j时取得极大值.显然,|QAiBi|、|MAiBi|在i=j时取得极大值.
当j (18) 由式(18)可知,NAiBi为i的线性函数且可正可负,故|NAiBi|在i=j+1或i=m时取得极大值.显然,|QAiBi|、|MAiBi|在i=j+1时取得极大值. 对比各区间内力极大值,可得杆件AiBi的轴力最大值、剪力最大值和弯矩最大值分别为 (19) (20) 1.3.2 杆件AiBi+1内力 取杆件AiBi+1为隔离体,则当i≠j时有 (21) 当i=j时有 (22) 当0≤i 可见,|NAiBi+1|在i=0或i=j-1时取得极大值,|QAiBi+1|、|MAiBi+1|在i=j-1时取得极大值. 当i=j时,将式(1)、(2)、(3)、(4)、(8)代入式(22)可得 当j 可见,|NAiBi+1|、|QAiBi+1|、|MAiBi+1|在i=j+1时取得极大值. 综上可知,杆件AiBi+1的轴力最大值、剪力最大值和弯矩最大值分别为 (23) (24) 1.3.3 杆件CiBi内力 取杆件CiBi为隔离体,则 (25) 当0≤i≤j时,将式(1)、(2)、(3)、(5)、(9) 代入式(25)可得 可见,|NCiBi|在i=0或i=j时取得极大值,|QCiBi|、|MCiBi|在i=j时取得极大值. 当j 可见,|NCiBi|在i=j+1或i=m时取得极大值,|QCiBi|、|MCiBi|在i=j+1时取得极大值. 综上可知,杆件CiBi的轴力最大值、剪力最大值和弯矩最大值分别为 |NCiBi|max=max{|NC0O1|,|NCjBj|,|NCj+1Bj+1|, |NCmBm|}<|NAjBj| (26) (27) 1.3.4 杆件CiBi+1内力 取杆件CiBi+1为隔离体,则 (28) 当0≤i≤j时,将式(1)、(2)、(3)、(5)、(9)代入式(28)可得 可见,|NCiBi+1|在i=0或i=j时取得极大值,|QCiBi+1|、|MCiBi+1|在i=j时取得极大值. 当j 可见,|NCiBi+1|在i=j+1或i=m时取得极大值,|QCiBi+1|、|MCiBi+1|在i=j+1时取得极大值. 综上可知,杆件CiBi+1的轴力最大值、剪力最大值和弯矩最大值分别为 (29) |QAj+1Bj+1| |MAj+1Bj+1| (30) 当m为偶数时,由式(19)、(23)、(26)、(29)可知,4类杆件在j=m/2时取得最大轴力为 (31) 对应杆件AjBj、AjBj+1的弯矩为 (32) 由式(20)、(24)、(27)、(30)可知,4类杆件在j=m/2时取得最大弯矩为 (33) 对应杆件Aj-1Bj、Aj+1Bj+1的轴力为 (34) 对应杆件CjBj、CjBj+1的轴力为 (35) 当m为奇数时,由式(19)、(23)、(26)、(29)可知,4类杆件在j=(m-1)/2或j=(m+1)/2时取得最大轴力为 (36) 对应杆件AjBj+1(或AjBj)的弯矩为 (37) 由式(20)、(24)、(27)、(30)可知,4类杆件在j=(m-1)/2或j=(m+1)/2时取得最大弯矩为 (38) 对应杆件Aj+1Bj+1(或Aj-1Bj)的轴力为 (39) 对应杆件CjBj+1(或CjBj)的轴力为 (40) 令A为杆件截面积,W为杆件抗弯截面系数,则移动集中荷载作用下所有杆件的最大正应力为 令剪叉杆件的材料密度为ρ,材料容许正应力为σ,采用弹性构件边缘屈服准则,则强度控制的剪式结构质量T为 (41) 定义剪式结构质量影响系数k为 (42) 令剪叉杆件形状系数γ为 将式(31)、(32)代入式(42)得 将式(33)、(34)代入式(42)得 将式(33)、(35)代入式(42)得 将式(36)、(37)代入式(42)得 将式(38)、(39)代入式(42)得 将式(38)、(40)代入式(42)得 由式(41)可知,质量影响系数k越小,即max{k1,k2,k3}或max{k4,k5,k6}越小,剪式结构可设计得越轻. 设定正常设计、使用条件下,5°≤θ≤85°,1≤m≤60,γ≥100.含γ的弯曲应力项为k的主要影响因子,并且max{k1,k2,k3}=max{k2,k3},max{k4,k5,k6}=max{k5,k6}. (43) (44) (45) (46) k5≤k6 k5>k6 (47) (48) (49) (50) 由式(44)、(46)、(48)和(50)可知,在正常设计、使用条件下,|f(θ)|、|g(θ)|、|φ(θ)|和|ω(θ)|均远小于1,可见对θ的变化不敏感. 由式(43)、(45)、(47)和(49)可知,k随m、γ增大而增大.方案设计阶段,选定m、γ后,通过令式(43)或(47)等于零可求得强度控制条件下剪式结构质量最小时对应的最优水平夹角θopt,结果见图5.由图可知,θopt随m增加而增大,随γ增加而减小,且逐渐趋于平缓. 将m、γ、θopt代入式(43)或(47),可得对应的kmin,结果见图6.由图可知,kmin随γ增加而增大.当m较小时,偶数标准单元的kmin小于相邻的奇数标准单元;当m较大时,kmin随m增加而增大. 图5 标准单元数m与最优水平夹角θopt的关系 图6 标准单元数m与最小质量影响系数kmin的关系 1) 采用结构力学分析方法,建立了移动集中荷载作用下两端固定铰支座剪式结构的一般力学模型,并以强度控制下剪式可展桥梁结构最轻质量设计为目标,获得剪叉杆件水平夹角与标准单元数、剪叉杆件形状系数之间的最优关系. 2) 质量影响系数对水平夹角的变化不敏感. 3) 最优水平夹角随着标准单元数的增大而增大,随着剪叉杆件形状系数的增大而减小,且逐渐趋于平缓. 4) 总体而言,最小质量影响系数随着标准单元数、剪叉杆件形状系数的增大而增大.因此,标准单元数、剪叉杆件形状系数建议采用较小值,且当标准单元数小于10时,建议采用偶数标准单元.


1.4 移动荷载作用下的杆件最大正应力

2 质量影响系数及参数分析
2.1 质量影响系数
2.2 最小质量影响系数及参数分析














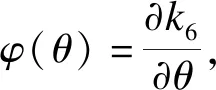




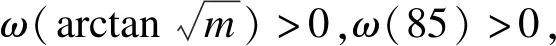


3 结论

