基于小波旁瓣相消器的轴承故障特征提取

苏润凡, 廖爱华,2*, 胡定玉,2, 师 蔚,2, 高伟民, 丁亚琦

(1.上海工程技术大学 城市轨道交通学院，上海 201620； 2.上海市轨道交通振动与噪声控制技术工程研究中心，上海 201620； 3.上海地铁维护保障有限公司 车辆分公司，上海 200235)

滚动轴承作为旋转机械设备重要零部件，广泛应用于各种行业的机械设备中[1-2]。因滚动轴承的损坏所引发的设备运行故障是旋转机械设备最常见的故障类型之一[3-4]，因此，对滚动轴承进行状态监测和早期缺陷检测具有重要意义。

在轴承故障诊断中，无须拆卸轴承的故障诊断技术越来越受到重视[5]。其中振动信号分析法应用最为广泛，发展也较为成熟[6]，但在高温、腐蚀等工作环境下，加速度传感器并不便于布置。实际应用中可以通过测量轴承的声压或声强来监测轴承状态[7]，声信号是非接触测量[8]，且声信号对轴承的早期缺陷也很敏感[9-10]，所以声信号分析可在不易布置加速度传感器和环境恶劣等多种场合下正常应用。麦克风阵列技术在机器人定位、语音信号处理等方面均展现出高性能，基于麦克风阵列的轴承故障诊断技术已被国外少数公司应用于列车轴承道旁声学诊断系统，其通过安装于铁轨两旁的麦克风阵列获取经过的列车声学信号，以此分析相应的列车轴承状态[11]，但国内外针对轴承声学故障诊断的阵列技术研究仍然相对较少。

Amarnath等[12]将经验模态分解(Empirical Mode Decomposition,EMD)应用到轴承声学信号检测中，实现了故障诊断的目的。Wiggins[13]提出的基于峭度最小熵解卷积(Minimum Entropy Deconvolution,MED)方法，其原理是利用熵值最小准则优化FIR滤波器参数，使得被滤波信号的熵值最小，增强故障冲击特性，现已成功证明了MED在减少传递路径和噪声对信号的影响方面具有很好的效果。Cabada等[14]利用频谱峭度(Spectrum Kurtosis,SK)波束形成在频域对旋转机械试验台中的故障小齿轮进行检测。Chen等[15]引入了一种时域峰度波束形成器，能利用麦克风阵列技术有效地定位和识别不同类型的车轮结构故障，验证了麦克风阵列技术进行故障诊断的有效性。然而在实际测量中，其声场往往非常复杂，混有其他声源产生的噪声信号，致使声学故障信号的信噪比很低，从而使得目标声源的声谱特征微弱，最终影响对轴承的状态识别。

针对此问题，提出一种基于小波旁瓣相消器的故障特征提取方法，首先建立基于声信号包络分析的基本分析方法，然后利用小波分析滤波器组将含噪故障轴承声信号变换到小波域，其次基于麦克风阵列技术进行小波域阵列广义旁瓣抵消波束形成，再通过小波综合滤波器组重构增强后的故障轴承声信号，对故障轴承声信号进行空域滤波，从而降低噪声带来的干扰，实现对故障轴承的有效诊断，最后通过实验对其有效性进行验证。

1 基础理论

1.1 声信号包络分析

滚动轴承声信号是轴承振动的产物，轴承振动发出的能量通过弹性媒介向外传递并引起空气的振动产生声波，继而产生滚动轴承声信号。当轴承出现故障时，声信号更为明显，滚动体在旋转过程中，与故障部位相接触，由于接触面不平顺产生冲击振动，该振动频率范围较宽，会引发轴承其他部件发生高频共振[16]，形成调制信号。

包络分析法[17]又称共振解调法或高频共振法，在齿轮和滚动轴承的故障诊断中可以有效提取故障特征频率信息，其核心内容是由低频冲击所引起的高频共振波进行包络检波和低通滤波，得到一个对应于低频冲击的而又被放大展宽了的共振解调波，最后对共振解调波进行频谱分析以诊断轴承是否发生故障。若发生故障，可根据故障特征频率诊断出故障类型。包络分析法应用于滚动轴承故障诊断的原理如图1所示。

1.2 基于传声器阵列的声信号提取

传声器阵列是将传声器按照特定排列方式组合而成的声信号采集设备，与单传声器相比，传声器阵列可以提供信号的空间分布信息，对接收到的信号进行空域滤波。波束形成算法则是对传声器阵列所接收到的信号进行延时求和，通过波束形成算法衰减各种噪声条件下的背景噪声来提供信号的空间信息，增强期望方向上的信号，并抑制其他方向上的噪声。

广义旁瓣相消(Generalized Sidelobe Canceller,GSC)波束形成是一种无约束的时域自适应波束形成，由传统的延时求和波束形成、一个阻塞矩阵处理单元和一个K阶FIR滤波器单元组成。GSC能够抑制相干噪声，在噪声消除领域起着重要的作用。

同时，故障诊断的重要因素之一是对信号所表现出的非平稳性进行研究,由于小波变换拥有时频分析、多尺度、多分辨率的特性，因此能对非平稳性信号进行较好的分析与诊断。本节在自适应波束形成与小波变换[18]理论的基础上，构建小波旁瓣相消器算法，基于小波滤波器组的旁瓣相消波束形成总体框图如图2所示。

图2 基于小波滤波器组的旁瓣相消波束形成结构图

在空间中放置一个平面传声器阵列，阵列上有M个传声器。对于传声器接收到的声压信号Pm(t)∈L2(R)(L2(R)表示平方可积的实数)，可以看作某一逐级逼近的极限。每级逼近都是用某一个低通滤波函数φ(t)对Pm(t)进行平滑的结果，当然逐级逼近的低通滤波函数φ(t)也进行逐渐伸缩，即找到L2(R)中的一系列函数φn(t)，用不同的分辨率或不同的尺度函数来逐级逼近Pm(t)。因此Pm(t)可以通过它在尺度正交基下的展开式得到，即

(1)

式中:φ0,n(t)=φ(t-n)，其中φ(t)为尺度函数。且

a0,n=〈xn(t),φ0,n(t)〉∈V0

(2)

定义Vj为尺度空间，Wj被定义为Vj在Vj-1中的正交补。应用多尺度分析中Vj=Vj+1⊕Wj+1，Pm(t)分解为

(3)

依此类推，把Pm(t)在V1内的部分看作原始信号进行分解，又得到V2和W2内的分量，再对V2内的部分进行分解，最终得到各个Wj(j=1,2,…，J)内的小波系数aj,n和dj,n,则式(3)可表示为

(4)

式中:aj,n和dj,n为j尺度上的展开式：

(5)

(6)

经过若干次的分解后，在达到一定的误差界或固定分解次数后分解终止。得到分解后的小波系数d1,n，d2,n,…，dj,n,aj,n，将这些小波系数分别经过自适应波束形成。固定波束形成输出信号可表示为

yc(m)=CTXj，j=1,2,…,J,J+1

(7)

式中:C=[C1,C2,…,CM]T为固定波束形成的权系数向量，且CTE=1，其中E是元素均为1的列向量，Xj=[dj,n(1),dj,n(2),…,dj,n(M)]，其中j=1,2,…,J。

则Xj+1=[aj,n(1),aj,n(2),…,aj,n(M)],为M个麦克风阵列信号经过小波分析滤波器组得到的第j个小波系数。

一个宽带旁瓣对消器包括一个波束形成器、一个阻塞滤波器和一个多输入对消器。小波系数Xj经阻塞矩阵B滤除其中的轴承信号得到噪声参考信号U(m)=[u1(t),u2(t),…,uM-1(t)]T,即

U(t)=BXj

(8)

式中:B为常用的Griffiths-Jim阻塞矩阵，如式(9)所示。

(9)

则多通道自适应滤波器的输出噪声参考信号为

(10)

式中:Wk(t)为第k个通道的自适应滤波器系数，其更新方程为

Wk(t+1)=Wk(t)+μy(t)U(t)

(11)

式中：μ为步长。则经小波滤波器组得到J+1个小波系数的自适应波束输出为

yj(t)=yc(t)-ys(t)，j=1,2,…,J+1

(12)

再通过小波综合滤波器组即可实现增强后的轴承故障信号重构。

1.3 诊断流程

利用小波旁瓣相消器可以有效提取声信号信息，相较于传统延时求和波束形成算法，能够极大限度地降低背景噪声对轴承故障信号的干扰，突出目标信号。具体过程包括以下内容。

① 利用小波分析滤波器组将含噪故障轴承声信号进行离散小波变换，将信号由时域变换到小波域。

② 在信号小波域，利用广义旁瓣抵消波束形成器对信号进行空域滤波，增强目标方向上的轴承信号。

③ 利用小波低频系数置零法，对低频系数置零，去掉故障轴承声信号中的低频噪声，进一步提高信号信噪比。

④ 通过小波综合滤波器组重构去噪后的故障轴承声信号，再对重构增强后的信号进行包络解调以获取调制后的低频信号。

⑤ 结合轴承故障特征频率信息，对轴承状态进行诊断。

2 实验分析

2.1 实验设置

使用轴承试验台采集轴承运行声信号，验证本算法的有效性。试验台主要由驱动电机、变频调速控制器、主轴、加载装置等构成，变频调速控制器可实现转速变频调节功能，加载装置通过垂直方向上的弹簧挤压进行径向加载。实验现场布置如图3所示。设置轴承试验台的转频为10 Hz，对应转速为576 rad/s，负载为200 N，采样频率为51.2 kHz，采样时长为6 s，传声器阵列为均匀线性阵列，阵元数为15，阵元间距为0.025 m，距离目标声源2 m，方位角为90°。为模拟实际环境噪声，录制实际列车通过声音并利用放置于故障轴承两侧音响播放作为干扰信号，信噪比约为-1.4 dB。

图3 实验现场布置图

本次实验选用轴承为SKF6016深沟球轴承，如图4所示，故障位于轴承内圈，采用电火花加工出一条宽约1 mm、深约1.5 mm、长约22 mm的裂纹，其他部位保持完好。表1为该故障滚动轴承的主要参数。

图4 SKF内圈故障轴承

表1 滚动轴承参数

(13)

根据实验电机转速和轴承参数，轴承内圈故障特征频率为79.6 Hz。

2.2 单传声器信号分析

为分析背景噪声对声信号诊断效果的影响，选取阵列中心位置处8号传感器测得的声信号进行分析。图5为无噪声环境下利用8号传感器测得轴承内圈故障声信号的时域图和包络谱图，从图5中可以看出传声器时域信号呈现出较为明显的包络特征，冲击特性比较明显，从对应包络谱图中可以发现轴承的故障特征频率及其多阶倍频成分。图5中轴承特征频率数值为78.6 Hz,2倍频为157.2 Hz,3倍频为235.8 Hz。 图5中实际特征频率与理论计算值略有不同，因为轴承在实际情况下，滑移是一定存在的，由此产生的轴承频率变化通常在 1%～2%之间，既可以作为计算值的偏差，也可以作为平均频率的随机变化，所以在后面的实验中当实际特征频率及倍频与理论值的偏差在1%～2%之间时，被认为其是轴承的特征频率和倍频。

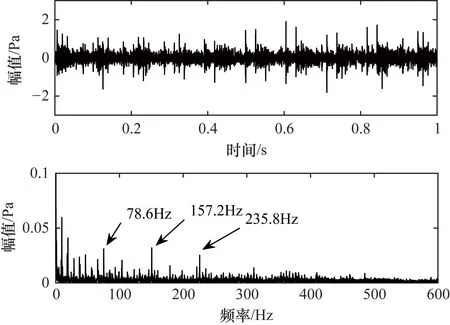
图5 无噪声轴承内圈故障信号时域图和包络谱图

图6为噪声环境下利用8号传感器测得轴承内圈故障声信号的时域图和包络谱图，由于噪声干扰，包络特征不再明显，冲击被淹没，包络谱分析无法提取出轴承故障特征。通过对比可以知道，单个传声器在没有强噪声干扰的环境下可有效提取故障特征，而在背景噪声影响较大的环境下则很难判断轴承是否存在故障及故障类型。

图6 有噪声轴承内圈故障信号时域图和包络谱图

最小熵解卷积(MED)常应用于旋转机械的故障特征增强[19]，减少声信号在传播过程中噪声和传递路径的影响，加强冲击特性。利用MED对故障轴承声信号进行处理，图7为处理后的信号时域图与包络谱图。从时域图可以看出轴承故障声信号的包络特征有所加强，但并不明显，包络谱中虽然可以找到轴承的故障特征频率及其多阶倍频成分，但并不显著，所以下面将对利用传声器阵列实现空域滤波以增强轴承故障特征进行研究。

图7 有噪声MED轴承内圈故障信号时域图和包络谱图

2.3 传声器阵列信号分析

下面利用传声器阵列信号进行分析。首先，通过延时求和波束形成方法对强噪声下声信号进行提取，提取到的信号和其包络谱如图8所示。图8中信号包络特征不明显，冲击被淹没，因而在有强噪声干扰的情况下，通过延时求和波束形成无法对轴承故障特征频率进行有效提取。

图8 延时求和波束形成轴承故障信号时域图和包络谱图

在强噪声下，利用小波分析滤波器组将含噪故障轴承声信号变换到小波域，然后进行小波域阵列广义旁瓣抵消自适应波束形成，将广义旁瓣抵消自适应波束形成的方位角设置为90°，使阵列指向性指向故障轴承，在抑制其他方向来源噪声的同时增强故障轴承方向声信号，再通过小波综合滤波器组重构增强后的故障轴承声信号，最后对重构增强后的信号进行包络解调并提取故障特征频率，处理后的轴承故障信号时域图与包络谱图如图9所示。

图9 小波旁瓣相消器轴承内圈故障信号时域图和包络谱图

从图9中可以看出较为明显的滚动轴承内圈故障频率和其倍频，另外在内圈故障特征频率的两侧分布有大量的滚动轴承所在轴转频的调制边频带，表征典型的内圈故障。小波旁瓣相消器可以对宽带故障轴承声信号的高低频分别进行不同尺度、频率的细节和概貌分析，实验结果证明本方法能够在噪声干扰下对轴承故障信息进行有效提取，且本方法的故障信息提取效果明显优于利用延时求和波束形成进行故障信息提取的效果。

2.4 方位角影响分析

波束形成技术具有指向性，可以通过对方位角的调整使传声器阵列接收所期望方向上的声信号，同时对其他方向的噪声进行抑制[20]。为分析入射方位角对声信号诊断效果的影响，将传声器阵列依次移动至固定位置，其他实验参数保持不变，实验阵列位置示意图如图10所示，阵列距离目标声源的距离和信号的入射方位角如表2所示。

图10 阵列位置示意图

根据表2中设定的方位角移动传声器阵列后，得到不同方位角下故障轴承声信号，采用小波旁瓣相消器提取的信号包络谱分别如图11所示。从图11中可以看出，即使在方位角改变的情况下，方法依然能够有效地在强干扰环境下提取出故障特征频率和其倍频。

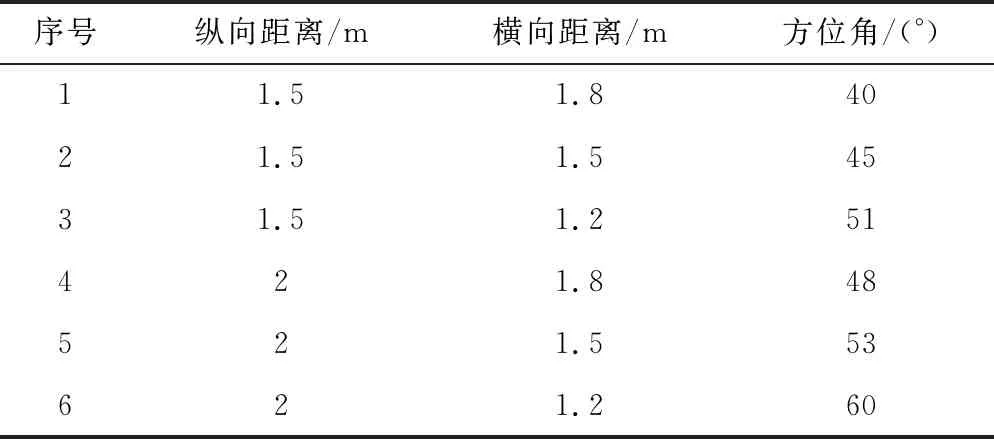
表2 阵列移动距离及入射方位角

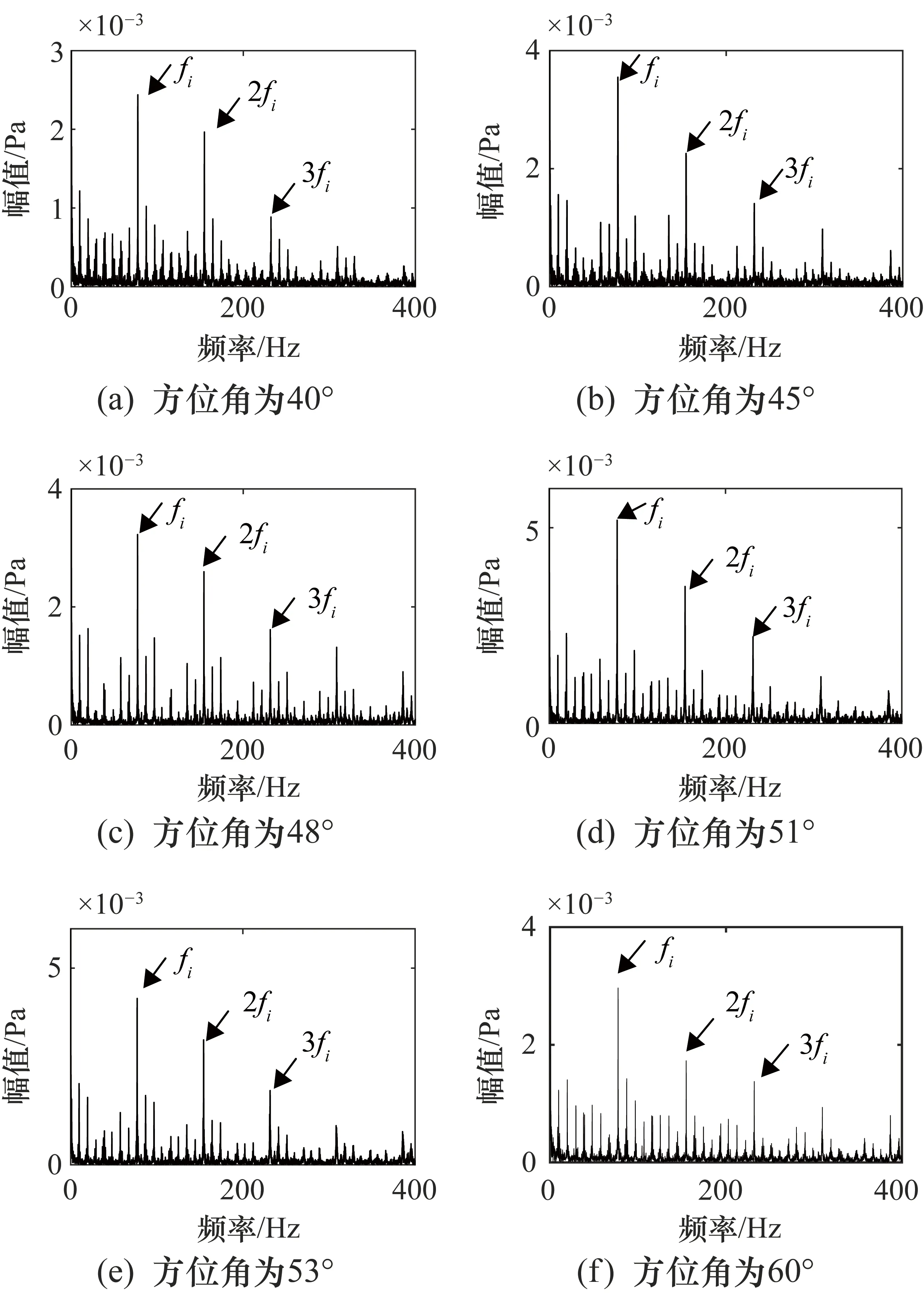
图11 不同方位角下本文方法提取的故障轴承声信号包络谱

3 结束语

针对强背景噪声下声信号提取轴承故障特征不显著的问题，提出了一种基于小波旁瓣相消器的故障特征增强方法。小波旁瓣相消器能够在强背景噪声下有效提取出轴承故障特征频率和其多阶倍频成分。与利用单传感器、MED和延时求和波束形成进行故障特征提取相比，本方法能够提取更多的轴承故障信息，轴承故障特征增强效果明显。实验结果证明，入射方位角对利用本方法进行提取轴承故障特征的影响很小，进一步验证了本方法的有效性、稳定性和工程应用价值。