风电叶片全尺寸静力加载测试载荷扰动分析

刘鹏辉， 邓 航， 谢红杰， 周爱国， 施金磊， 余后跃

(1.株洲时代新材料科技股份有限公司，湖南 株洲 412007； 2.同济大学 机械与能源工程学院，上海 201804)

目前，风电行业是新能源领域重点发展的新兴产业，截至2021年底，全球累计海上风电容量达到56 GW，相较于2020年增长了58%[1]。风电叶片作为整个机组中重要的组成部分，其结构强度和设计的可靠性是保证机组安全稳定运行的重要环节。根据国际电工委员会IEC 61400-23的风电叶片标准[2]，叶片设计厂家需要对新研制的叶片进行全尺寸结构静力加载试验。在叶片静力加载试验中，需要对叶片采用多点加载的方法，将叶片实际运行过程受到的极限载荷等效为多个加载点的静力载荷，多点静力载荷通常需要按照一定的流程逐步施加在叶片上，使被测叶片的弯矩分布与实际弯矩分布尽可能一致，从而模拟整个叶片的受力情况。在实际静力加载试验中，由于多点加载力的耦合效应以及动滑轮和加载缆索构成的弹簧系统抖动产生的载荷扰动，均会使叶片在加载测试中受到波动的载荷，进而导致叶片受到的实际载荷曲线与目标载荷曲线之间的误差不能满足精度要求，该情况也是叶片静力加载过程中普遍存在的问题[3]。

针对上述问题，考虑到神经网络PID 自整定算法具有较强的适应性和学习能力[4]，张鑫鑫等[5]提出一种模糊控制和预测理论相结合的动态控制算法以实现叶片五点静力加载解耦控制；乌建中等[6]通过BP(Back Propagation)神经网络PID自整定算法实现了三点静力加载的解耦控制；周爱国等[7]提出一种变步长BP神经网络自整定算法，通过改变刚度和耦合矩阵的方式实现了叶片六点静力加载解耦控制。上述研究主要侧重于对加载点之间的加载力相互耦合的现象提出改进的解决方案，能够在实际的静力测试中减小加载力之间的耦合效应，提高加载精度。然而除了多点加载力之间的耦合效应会降低测试精度外，动滑轮和加载缆索构成的弹簧系统在加载过程中产生的动态响应也会产生载荷扰动，进而影响叶片所受到的测试载荷。

针对动滑轮和加载缆索构成的弹簧系统的动态特性对叶片产生载荷干扰的问题，本文建立了叶片-加载缆索-动滑轮动力学模型，并使用Simulink和Adams对该动力学模型进行仿真，分析了叶片和动滑轮之间位置参数对叶片和动滑轮振动特性的影响。最后对某型叶片采取四点静力加载试验，对比验证了叶片和动滑轮之间的位置参数对载荷曲线精度的影响。

1 叶片-加载缆索-动滑轮动力学模型

风电叶片全尺寸静力加载测试系统主要由叶片、加载缆索、动滑轮和加载支架构成[8]，如图1所示。叶片安装在测试基座上，加载支架通过动滑轮对叶片施加载荷，叶片在多点加载力的作用下发生形变。此外，叶片和动滑轮之间连有加载缆索。由于加载缆索的弹性变形较小，在现有的研究分析中，通常把加载支架和叶片之间的部件视为刚性，从而忽略了动滑轮和加载缆索构成的弹簧系统动态特性对叶片的影响。而在实际的多点静力加载试验中，动滑轮和加载缆索的抖动现象时有发生，为了准确分析动滑轮抖动对叶片的影响，需要建立叶片-加载缆索-动滑轮动力学等效模型来分析动滑轮和加载缆索构成的弹簧系统对叶片的影响，如图2所示。

图1 风电叶片全尺寸静力加载测试系统

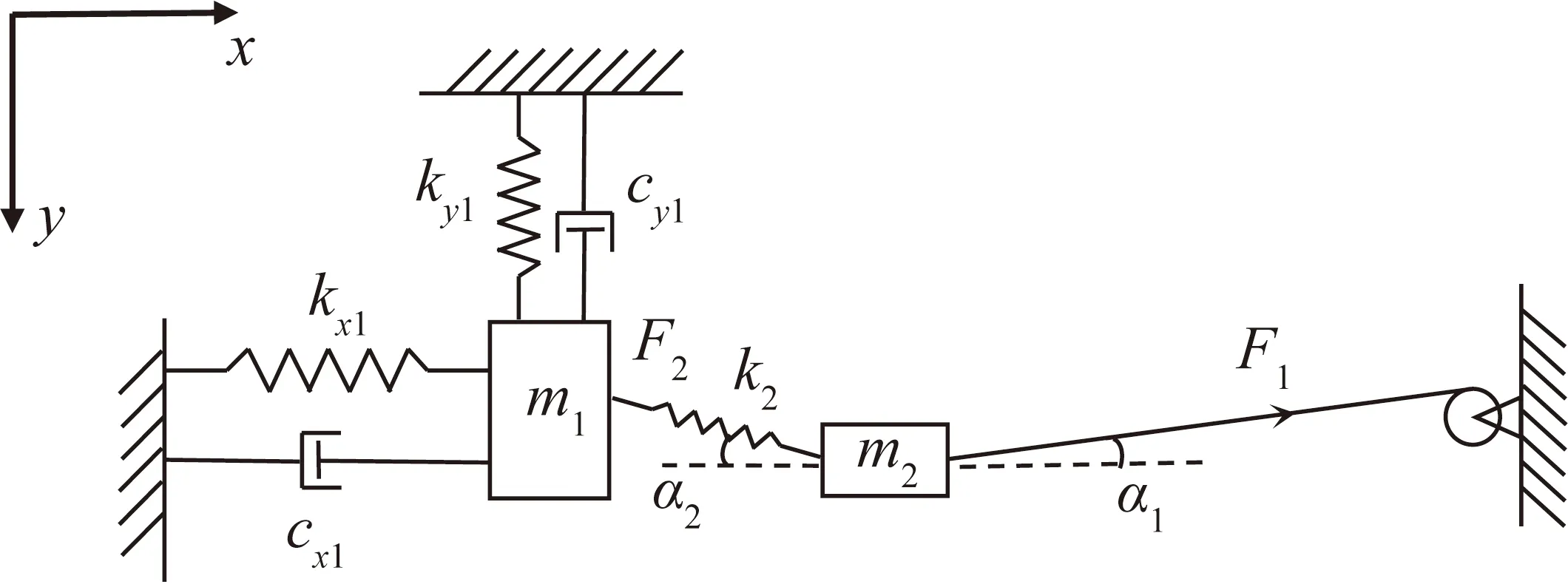
图2 叶片-加载缆索-动滑轮动力学等效模型

为了准确分析动滑轮和加载缆索构成的弹簧系统对叶片产生的影响，简化叶片模型，忽略动滑轮至加载支架间的加载缆索的弹性，选取其中一个加载点进行受力分析。根据牛顿第二定律，可以分别建立该加载截面处叶片-加载缆索-动滑轮系统在摆振方向(x方向)和挥舞方向(y方向)的动力学微分方程：

(1)

式中:F1为加载支架提供的加载力；F2为加载缆索上的弹性力；kx1、ky1、cx1、cy1分别为叶片在x和y方向的等效刚度和等效阻尼；k2为加载缆索的刚度；m1和m2分别为叶片和动滑轮的等效质量；α1为加载力F1与水平方向的夹角；α2为加载缆索弹性力F2与水平方向的夹角；x1和x2分别为叶片和动滑轮在x方向的位移；y1和y2分别为叶片和动滑轮在y方向的位移。

其中，动滑轮相对于叶片的初始位置与加载缆索初始长度和加载点的初始加载力大小有关，为了便于分析，分别用x20和y20表示动滑轮和叶片的相对位置。此外，式(1)中的夹角为

(2)

式中：x20为动滑轮相对于叶片在x方向的相对位置；y20为动滑轮相对于叶片在y方向的相对位置；L为加载点和叶片初始位置之间的距离。

由式(1)和式(2)分析可知，叶片的动力学响应受到加载缆索弹性力F2的影响，弹性力F2又会受到动滑轮和加载缆索构成的弹簧系统的影响。因此，动滑轮的振动特性和加载缆索的弹性形变不可忽略。此外，由式(2)可知，当动滑轮和叶片初始位置相同时，即x20=0和y20=0时，动滑轮和叶片不存在夹角，即动滑轮和叶片处于同一位置，动滑轮和叶片的运动状态一致。

2 仿真模型

2.1 Simulink仿真分析

根据建立的动力学微分方程，可利用MATLAB软件搭建等效的Simulink模型[9]。为了对比有无动滑轮和加载缆索构成的弹簧系统的差异性，分别建立了叶片-加载缆索-动滑轮的Simulink模型和叶片-加载力的Simulink模型。

选取某型56 m叶片的等效参数、动滑轮的初始参数和加载缆索的参数，如表1、表2所示。查阅机械振动可知[10]，加载缆索的等效刚度约为等效杆单元刚度的1/5，故选取表3所示的加载缆索参数。

表1 叶片的等效参数

表2 动滑轮的等效参数

表3 加载缆索的等效参数

加载点和叶片初始位置之间的距离L=15 m，加载力F1为斜坡加载，其最大值为100 kN，如图3所示。

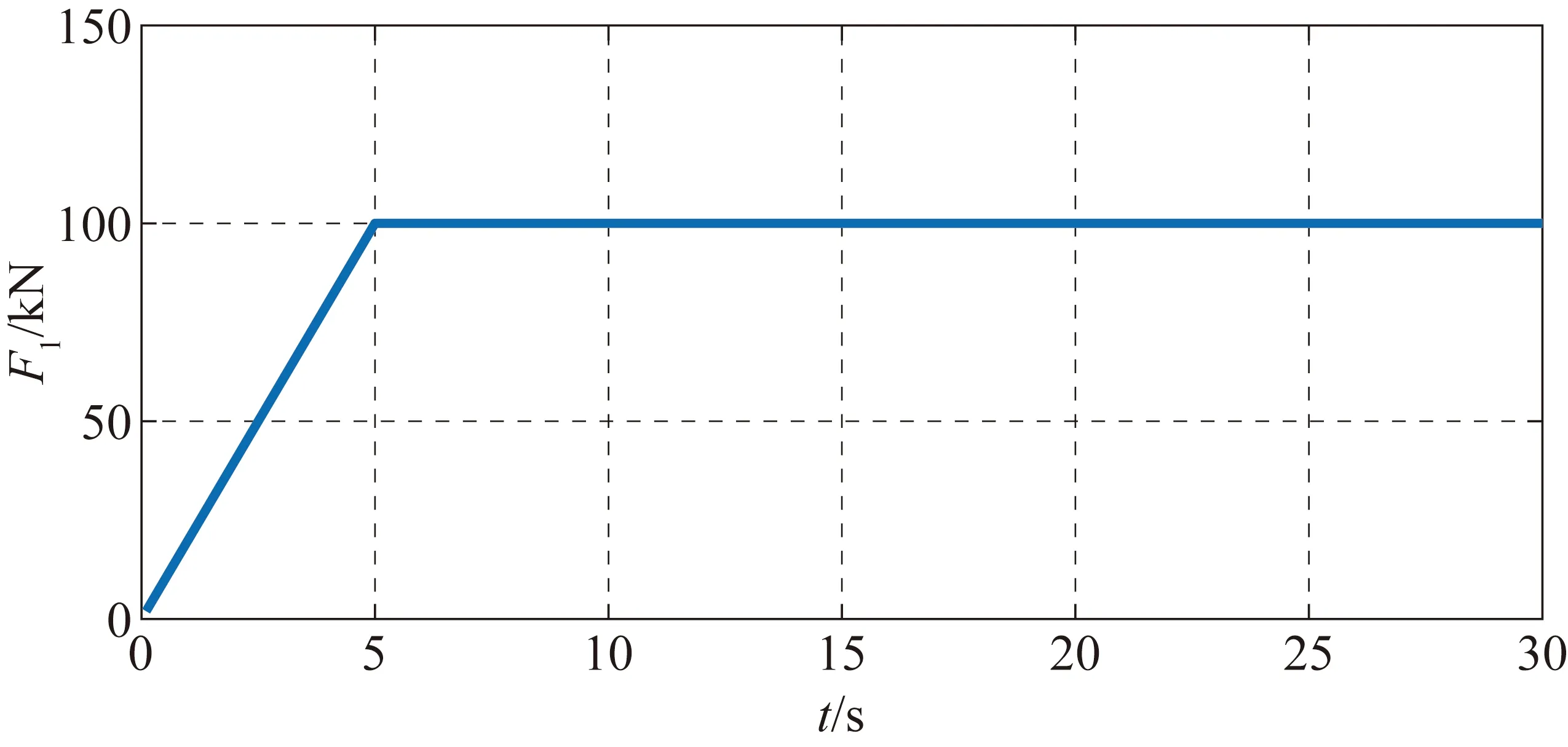
图3 加载力F1的作用形式

2.1.1 叶片-加载缆索-动滑轮模型分析

首先,对图2所示的叶片-加载缆索-动滑轮模型进行仿真分析，使用的参数如表1～表3所示，加载力F1的作用形式如图3所示。叶片和动滑轮在挥舞和摆振方向的运动响应如图4所示。

图4 叶片和动滑轮的运动响应

在该工况下，从图4(a)可以看出，在挥舞方向，在加载力F1作用下， 叶片和加载缆索的响应为衰减曲线，最终达到接近于零的稳态值。此外，由于叶片在挥舞方向的阻尼大于摆振方向的阻尼，故叶片和动滑轮在挥舞方向的响应衰减较快；从图4(b)可以看出，在摆振方向，随着加载力F1的增加，叶片和加载缆索的位移也波动增加，当加载力F1趋于恒定时，叶片和加载缆索的稳态响应也趋于恒定，但也存在瞬态响应的幅值波动干扰。

2.1.2 叶片-加载力模型分析

为了对比叶片-加载缆索-动滑轮模型的结果，还构建了叶片-加载力模型进行对比分析。在叶片-加载力模型中忽略了动滑轮和加载缆索构成的弹簧系统，故也不考虑加载缆索的微变形，加载支架直接对叶片施加加载力，即在图2的等效模型中忽略动滑轮以及叶片和动滑轮之间的加载缆索。此时，叶片在加载力F1的作用下发生形变，结合图2可知，在平衡状态对叶片施加摆振方向(x方向)载荷时，叶片在摆振方向运动，在挥舞方向(y方向)基本不发生运动。基于表1～表3所示的初始参数，可仿真获得叶片的运动特性。加载系统是否考虑动滑轮-加载缆索的叶片运动特性如图5所示。

图5 加载系统是否考虑动滑轮-加载缆索的叶片运动特性

从图5(b)可以看出，在挥舞方向，包含动滑轮的模型其振动波动较为明显，而不包含动滑轮的模型其动态响应很快趋于稳定，这也符合实际加载情况；从图5(a)可以看出，在摆振方向，具有与挥舞方向类似的现象。 因此当加载系统中含有动滑轮-加载缆索时，由于动滑轮和叶片之间加载缆索的弹性变形，会导致加载系统受到该弹簧系统动态干扰的影响，即叶片受到载荷扰动，实际载荷曲线和目标载荷曲线会产生振荡误差。虽然载荷扰动会逐渐衰减，但衰减的速率会直接影响静力加载的测试精度。

2.2 Adams仿真分析

由于加载支架的位置受限于测试大纲和现场安装条件，且叶片的属性参数和测试设备无法改变，因此，仿真主要分析叶片和动滑轮之间的初始相对位置x20和y20对加载系统振动特性的影响。

为了更准确地分析叶片加载缆索对叶片的振荡干扰，在Adams软件建立叶片-加载缆索-动滑轮Adams动学模型[11]，如图6所示。主要初始参数如表4所示。修改的变量为动滑轮相对于叶片的相对位置x20和y20，即改变了加载缆索的长度，加载缆索相对位置变化参数如表4所示。在Adams仿真模型中，以动滑轮的初始位置为起始坐标，并考虑了叶片和动滑轮的自重产生的位移。7种工况下叶片和动滑轮在挥舞方向上的动态特性，如图7和图8所示。

表4 加载缆索相对位置变化参数表

图6 叶片-加载缆索-动滑轮Adams动力学模型

图7 相对位置x20变化时叶片和动滑轮振动特性

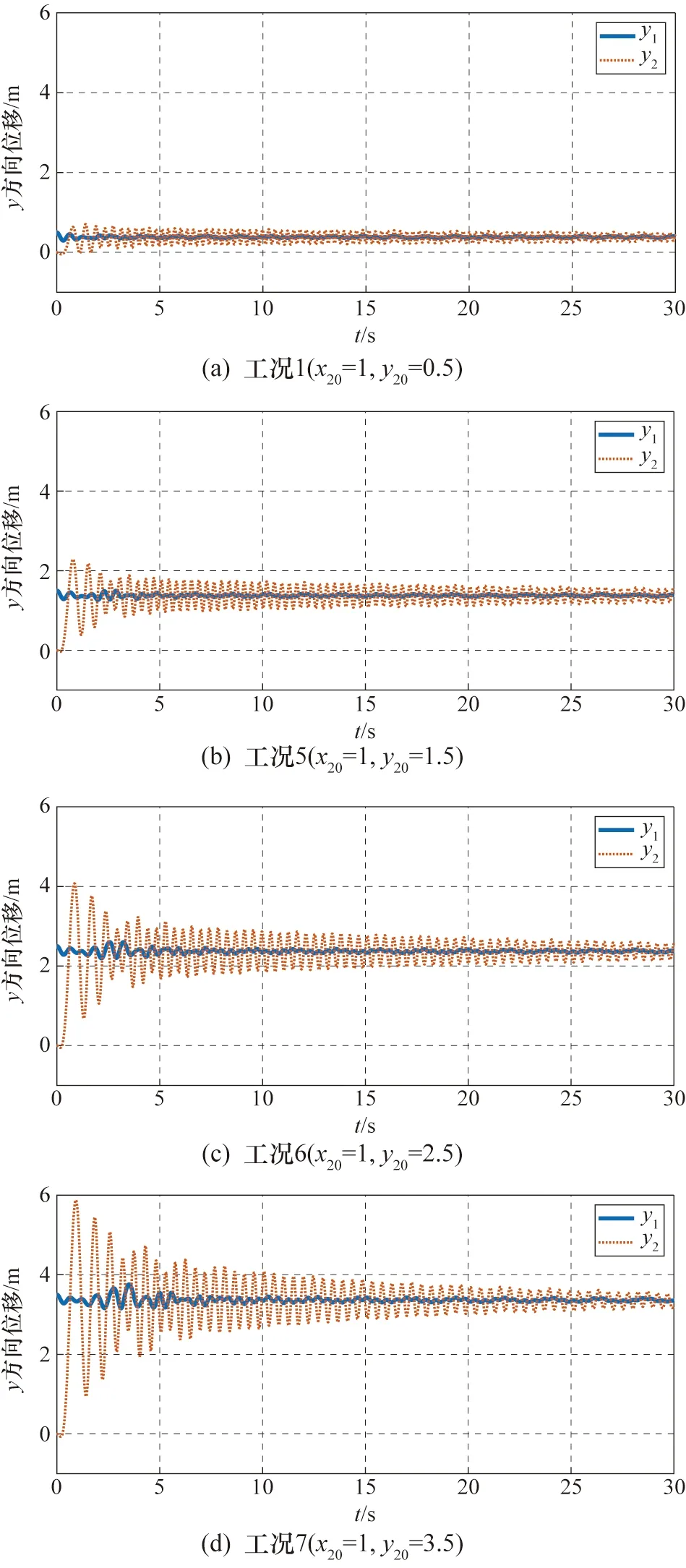
图8 相对位置y20变化时叶片和动滑轮振动特性

从图7可以看出保持动滑轮和叶片的相对位置y20不变，增大x20，动滑轮在挥舞方向的振动幅值逐渐减小，也能够快速地接近稳态，而叶片在挥舞方向的振动幅值减小情况不明显，但波形变为更加顺滑。即工况1～工况4加载缆索的位置变化有利于改善动滑轮受到的扰动，由于动滑轮整体的振荡幅值较小，故对叶片产生的载荷干扰也较小，扰动现象不明显。

从图8可以看出，保持动滑轮和叶片的相对位置x20不变，增大y20，动滑轮在挥舞方向的振动幅值逐渐增大，衰减到稳定值较慢；叶片在挥舞方向的振动幅值也逐渐增大。即工况1和工况5～工况7中，加载缆索的位置变化会加大动滑轮受到的扰动，由于动滑轮整体的振荡幅值较大，故对叶片产生的载荷干扰也较大，载荷扰动现象更加明显。

此外，图8(d)和图4(a)工况等同，换算至同一参考系，可验证所建立的叶片-加载缆索-动滑轮动力学模型和Simulink模型的准确性。

2.3 仿真结果分析以及改进措施

根据Simulink和Adams的仿真结果可知，在不考虑动滑轮和加载缆索构成的弹簧系统的情况下，叶片在加载力的作用下，其振幅能够很快达到稳态值，叶片在挥舞和摆振方向上基本不会受到弹簧系统带来的载荷干扰。在考虑动滑轮和加载缆索构成的弹簧系统的情况下，叶片和动滑轮的振动特性与两者之间的相对位置有关，即与加载缆索的姿态有关，挥舞方向的相对位置越大，叶片和动滑轮受到的振荡干扰也越明显，对叶片受到的载荷曲线的精度产生了较大的影响。

基于上述分析，为了进一步削弱静力加载中加载抖动的效应，可从以下3个方面进一步改进：

① 叶片和动滑轮之间的加载缆索采用刚性更大、形变量更小的连接，增大图2中的刚度k2。

② 在静力加载测试开始前，需要将动滑轮位置尽量拉至与叶片同一水平位置处，即减小叶片和动滑轮的相对位置y20，以减小载荷扰动幅值。

③ 当叶片和动滑轮的相对位置y20已经达到最小值时，可适当增大叶片和动滑轮的相对位置x20，进一步加速减小动滑轮的振动幅值。

3 试验验证

为了验证改进措施的效果，对某型80 m叶片进行四点静力加载试验，如图9所示，阶段载荷分别为20%、40%、60%、80%、100%。在静力测试之前，将加载点1～加载点4的动滑轮尽量拉至与叶片水平，其中加载点1～加载点3的加载缆索摆振相对位置x20均为4 m左右，加载点4的加载缆索摆振相对x20为3 m左右，且其挥舞相对位置y20相较于其余三点略大。由于叶片无法直接和加载缆索进行连接，则叶片和加载缆索之间还须增加高强度绑带作为过渡，动滑轮上安装有拉力传感器以反馈叶片实际受到的载荷。多点静力加载测试结果如图10所示。

图9 叶片四点静力加载试验现场

从图10可以看出，在加载的最初阶段，各加载点受到的实际载荷和目标载荷之间的误差较大，这是因为在加载的初始阶段，加载系统还未稳定，叶片受到多点加载耦合以及动滑轮和加载缆索构成的弹簧系统抖动的影响，产生了较大的载荷误差。在后续加载阶段中，加载耦合效应得到缓解，加载缆索形变为主要的外部干扰。此时，加载点1～加载点3的实际载荷与目标载荷接近，受到的振荡干扰不明显，各保持阶段的最大加载误差不超过3%；而加载点4的载荷曲线在加载力从保持阶段转为增加阶段时，实际载荷曲线受到振荡干扰较为明显，此时与目标载荷曲线的误差较大，保持阶段的最大加载误差接近10%。由于叶片受到的测试载荷是由动滑轮上的拉力传感器测得的，故动滑轮的振动也会加剧测试载荷的误差。但这也验证了保持动滑轮和叶片的相对位置y20较大、x20较小时，叶片和动滑轮在加载缆索弹性变形的作用下，其波动振幅减小，且振幅趋于稳定的速度较快，对叶片的载荷干扰和测试载荷的误差也越小，故精度越高。

4 结束语

针对动滑轮和加载缆索构成的弹簧系统对叶片测试载荷产生振荡干扰的问题，建立了叶片夹具、动滑轮和加载点的动力学模型，使用Simulink和Adams对该动力学模型进行仿真，分析了叶片夹具和动滑轮之间的连接段初始参数和叶片以及动滑轮振动特性的影响。仿真结果显示，减小叶片和动滑轮的挥舞相对位置y20，有利于减小叶片受到的载荷扰动，若叶片和动滑轮的相对位置y20已经达到最小值，可适当增大叶片和动滑轮的摆振相对位置x20，以进一步加速减小动滑轮对叶片的扰动。最后，对某型80 m叶片采取多点静力加载试验，验证了改进相对位置参数有利于进一步降低载荷曲线受到的振荡载荷，从而可提高测试精度。