动载荷对轨道车辆电机轴电流的影响

覃静雨，师 蔚，廖爱华，胡定玉

（上海工程技术大学城市轨道交通学院，上海 201620）

变频供电驱动交流电机以其良好的运行和控制特性，在轨道交通领域得到了广泛的应用，但也带来了不可避免的轴承电蚀问题。

刘瑞芳等［1-2］对电机内部杂散电容进行计算，分析了轴承电容与电机轴承电机转速和轴承载荷间的关系，提出了一种电机轴电流高频模型，研究轴承油膜被击穿后的轴电流、轴电压的特性。Tischmacher 等［3］通过滚珠轴承试验台，研究外部激励振动对润滑油膜与轴承放电活动的影响。朱显辉等［4］基于电动汽车四分之一振动模型，分析电动汽车行驶时路面不平度激励的随机振动引起的轴承载荷变化对驱动电机轴电容的影响。

虽然许多学者对电机轴承的轴电流进行了研究，但由于轴电流击穿机理复杂，国内外关于动载荷对轨道车辆电机轴电流影响的研究仍显不足。本文从轨道激励的车辆振动模型入手，分析轨道车辆转向架构架振动引起电机轴承动载荷，建立基于动载荷的解析模型，研究了不同振动加速度下的动载荷对电机轴承轴电容与相关参数及对电机轴承轴电流与轴电流密度的影响效果。

1 轨道不平顺激励的车辆振动模型

1.1 车辆垂向振动动力学模型

轨道车辆振动系统是一个复杂的系统，电机轴承运行时主要受到垂向力作用，分析时可对车辆的数学模型进行简化，仅考虑车辆的沉浮运动，得到轨道车辆的垂向振动模型如图1所示［5］。其中，轨道车辆的车体、转向架和轮对均视为刚体，忽略轮对的刚度和阻尼。车辆以速度v行驶在轨道线路上；Zc为车体的垂向位移；Zt为转向架浮沉运动的垂向位移；Zw为车轮的垂向位移，Z0为轨道不平顺的位移；Kpz、Cpz为轮对与转向架耦合的一系悬挂刚度和阻尼；Ksz、Csz为转向架与车体耦合的二系悬挂刚度和阻尼。

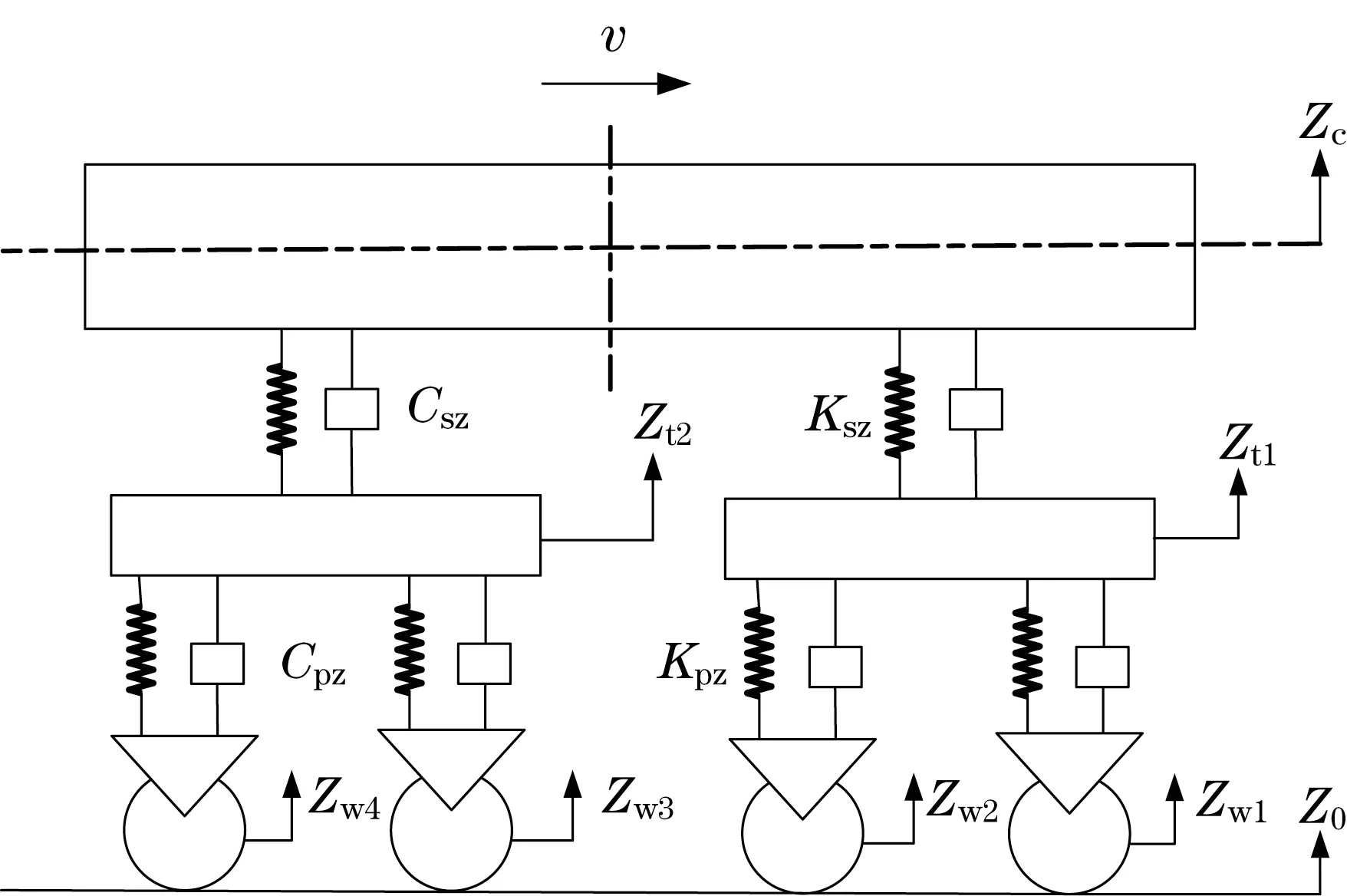
图1 车辆垂向振动模型Fig.1 Vehicle vertical vibration model

仅考虑车辆的沉浮运动，对轨道车辆垂向振动模型进行受力分析，车辆垂向振动统一模型的微分方程可由D′Alembert原理推导获得［6］。

1.2 轨道不平顺激励的确定

将轮对与轨道视为一体，则轮对的垂向位移Zw与轨道不平顺施加在轮轨上的激扰Z0相同。本文根据轨道不平顺的时域模拟原理，由美国五级谱的轨道高低不平顺解析表达式推导得到美国五级轨道位移输入Z0的时域表达式：

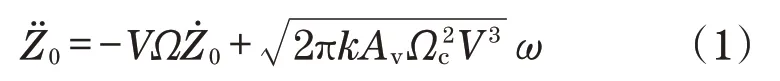
轨道车辆行驶的路况十分复杂，常会经过道岔、桥梁、隧道等特殊的轨道位置，会引起轨道车辆产生较大的振幅。地铁车辆最高速度一般不超过80 km/h，为研究车辆在受到偶然大振幅轨道激励时的振动情况，利用轨道激励函数来模拟车速在80 km/h、轨道不平顺最大为0.025 m 的阶跃轨道激励如下：

1.3 车辆振动时域仿真与分析

根据车辆垂向振动模型数学表达式，在Simulink 中建立地铁车辆垂向运动数值仿真模型。将某一地铁车辆的具体参数引入到车身振动的仿真分析模型中，所选用地铁的车身质量、刚度以及阻尼系数等参数分别为Mc=34 t，Mt=2.8 t，kpz=3.68×106N/m，ksz=1.98×106N/m，Cpz=6.6×104N·m·s-1，Csz=6.4×104N·m·s-1。以美国五级谱轨道不平顺时域激励为输入，得到不同速度下的转向架构架的振动加速度变化如图2（a）所示，其幅值与均方根值分别在0～9.68 m/s2和0～2.35 m/s2内变化。将车速在80 km/h 的阶跃轨道激励作为系统的输入，得到转向架振动加速度变化如图2（b）所示，其峰值约为65 m/s2。

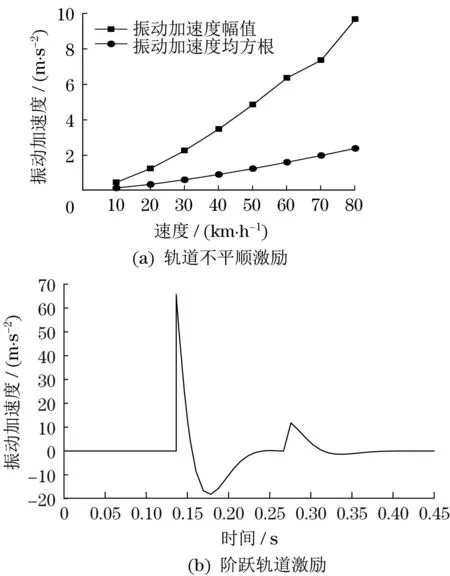
图2 不同轨道激励的转向架加速度响应Fig.2 Bogie acceleration response under different track excitation

2 动载荷对电机轴承等效电容的影响

2.1 电机轴承电容的结构

本文研究某轨道车辆使用的三相异步电动机YQ-190-8H，电机传动端采用SKF 圆柱轴承NU216ECM，轴承的滚珠数N=18，轴承内径da=80 mm，轴承外径D=140 mm，滚子直径Dw=16 mm。假设轴承处于极端的受力情况，轴承动载荷、转子质量及单边磁拉力三者同向且相互叠加，轴承受力分析如图3所示。

图3 轴承受力分析Fig.3 Bearing stress analysis

图3中，电机作用到转轴上的力为转子自重M1g1、定子与机壳产生的动载荷M2g2、单边磁拉力P的合力。圆柱滚子轴承单个滚动体所受最大动载荷Qmax为

式中：M1为转子质量；M2为定子与机壳质量；g1为转子重力加速度；g2为电机振动加速度；c为重心距离驱动端轴承距离；d为重心距离非驱动端轴承距离；Nz为轴承受载滚动体个数，对于圆柱滚子轴承Nz≈N/5。

2.2 电机轴承轴电容分析与计算

电机轴承电容可看成由2 个面积相等的平板和电解质为润滑脂的油膜构成的平板电容，其等效电容结构如图4所示。

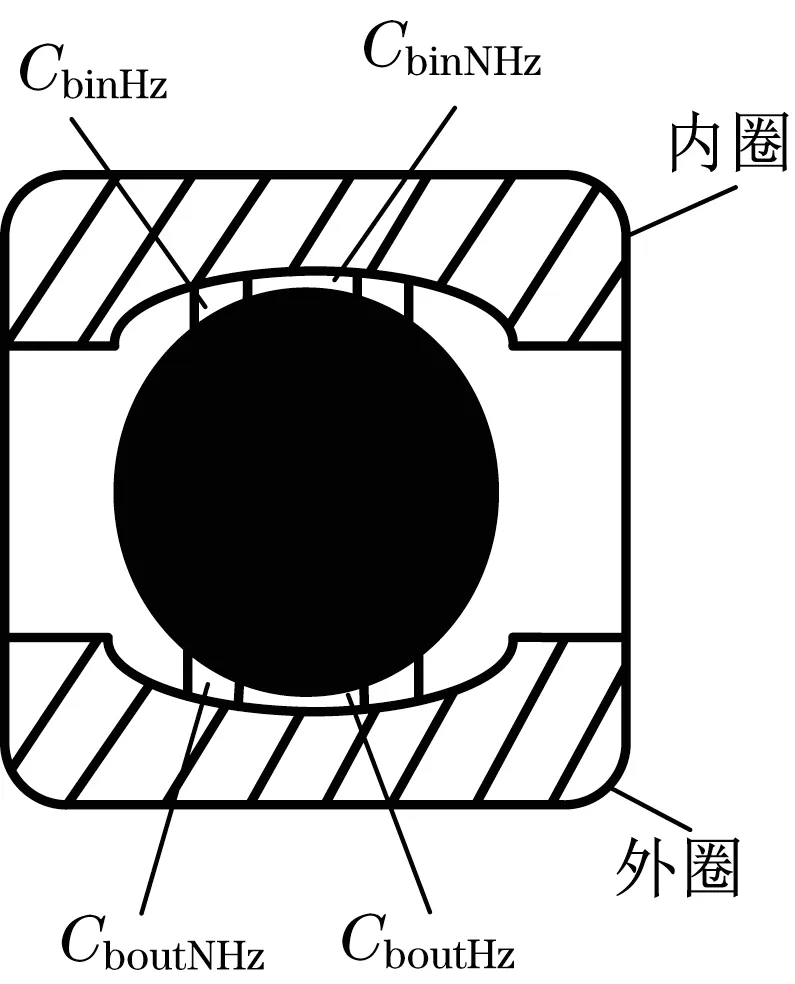
图4 轴承等效电容结构Fig.4 Bearing equivalent capacitance structure

图4中，电机轴承单个轴承滚子的等效电容可以分为2 个部分：在赫兹接触面内，由滚动体、油膜、滚道形成的赫兹接触电容CbHz；CbinHz、CboutHz为轴承内滚道与外滚道形成的赫兹接触电容。在赫兹接触面外，由滚动体、空气、滚道形成的非赫兹接触电容CbNHz；CbinNHz、CboutNHz为轴承内滚道与外滚道形成的非赫兹接触电容。单个滚动体内滚道形成的总轴承电容Cbin与外滚道形成的总轴承电容Cbout分别为

单个轴承滚子的总电容可看成轴承内外滚道等效电容串联，由于每个滚动体间形成的电容差别较小，为了简化计算，本文以受载荷最大的滚动体为参考，得到电机轴承的总电容Cb为

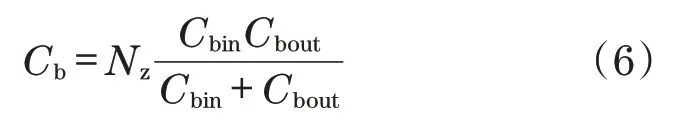
圆柱滚子轴承接触区域内滚子与滚道间接触变形的平面投影如图5所示［8］。

图5 圆柱滚子轴承接触变形Fig.5 Cylindricalrollerbearingcontact deformation

单个轴承滚子与内外圈滚道间赫兹接触区域的等效电容为

式中：ε0为真空介电常数；εr为润滑脂的介电常数；AH为赫兹接触面积；hc为滚动体与滚道间的最小油膜厚度。

赫兹接触面积AH的计算公式为

式中：L为滚子与滚道的有效接触长度；R为当量曲率半径；E′为当量弹性模量。

根据道森和希金森的纯滚动假设，可以推导出圆柱滚子轴承中滚子和内外圈滚道之间的弹流油膜厚度公式为［7］

式中：α为润滑脂的黏压系数；η0为润滑脂的动力黏度；W=Qmax/L；n为轴承工作转速；γ=Dw/dn，dn为轴承平均直径。

圆柱滚子轴承在非Hertz 接触部分等效电容CbNHz的计算公式为

式中：r为圆柱滚子底面半径；r′为XOZ平面滚子上的点与滚道间隙为100hc时该点到接触点的距离。

2.3 电机动载荷对轴承电容参数的影响

结合车辆实际运行工况，轨道车辆通常可分为变速和匀速两种运行工况，本文取车辆在0～80 km/h 的变速工况以及42 km/h 的匀速工况，分析不同工况下的电机振动变化对轴承赫兹接触面积与油膜厚度的影响。

2.3.1 电机动载荷对轴承赫兹接触面积的影响

轴承的赫兹接触面积是计算轴承电容的重要参数之一，由式（8）得到不同的振动加速度下的轴承动载荷对赫兹接触面积的影响如图6所示。

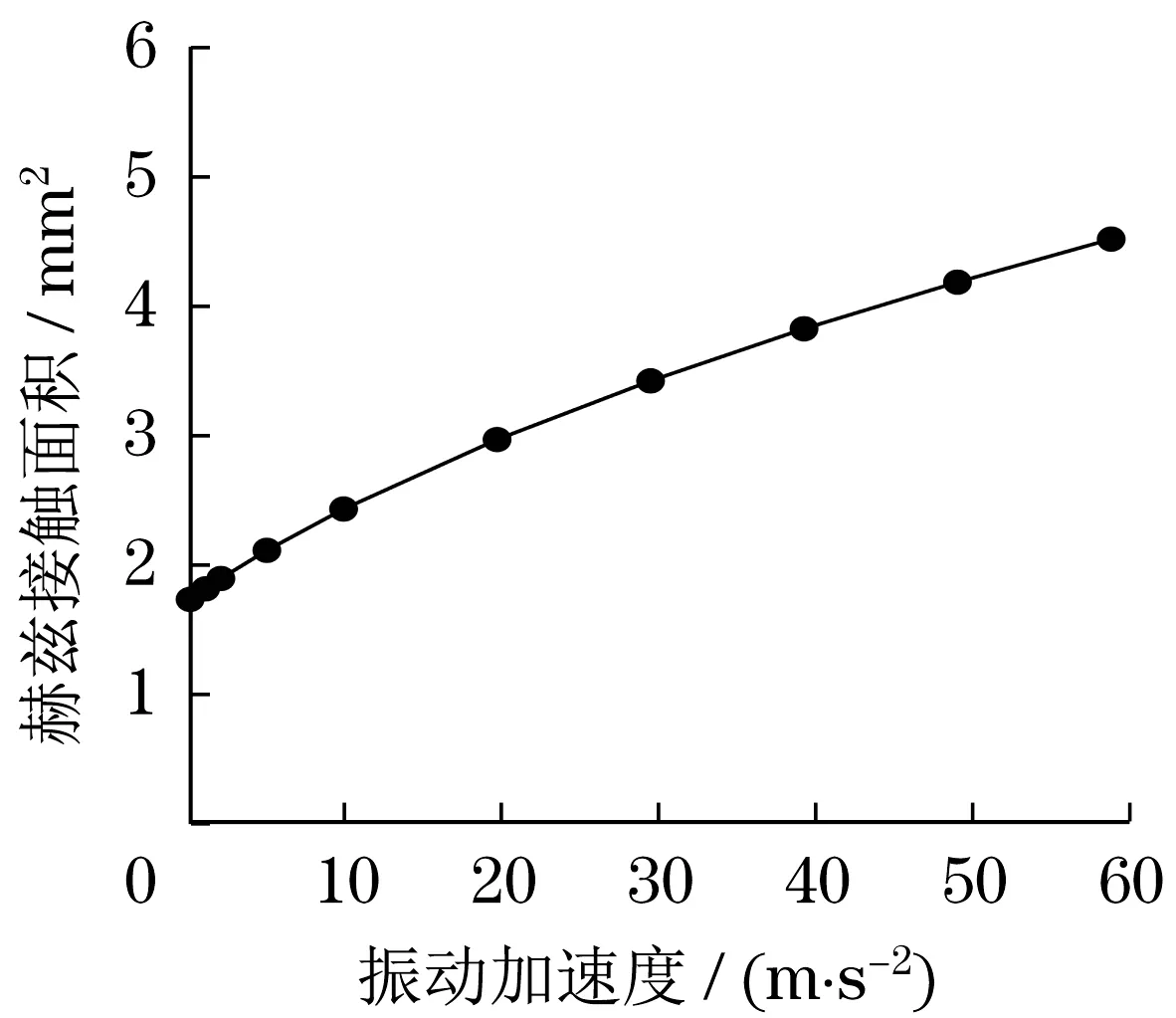
图6 轴承赫兹接触面积随振动加速度的变化Fig.6 The variation of Hertz contact area of bearing with vibration acceleration

图6表明，振动加速度由0 m/s2增加至58.8 m/s2，轴承的动载荷逐步增大，轴承滚动体与滚道间的赫兹接触面积增大了近2倍。

2.3.2 电机动载荷对轴承的油膜厚度的影响

轴承的油膜厚度同样是影响轴承电容大小的重要参数。轴承油膜厚度与电机的转速、轴承的载荷、温度以及润滑脂的性能参数等多种因素相关。假设在较为恶劣的情况下，轴承工作温度为80 ℃，黏压系数α为2×10-8Pa-1和动力黏度η为0.023 76 Pa·s，根据式（13）得到不同工况下电机轴承油膜厚度随着电机振动加速度的变化如图7所示。

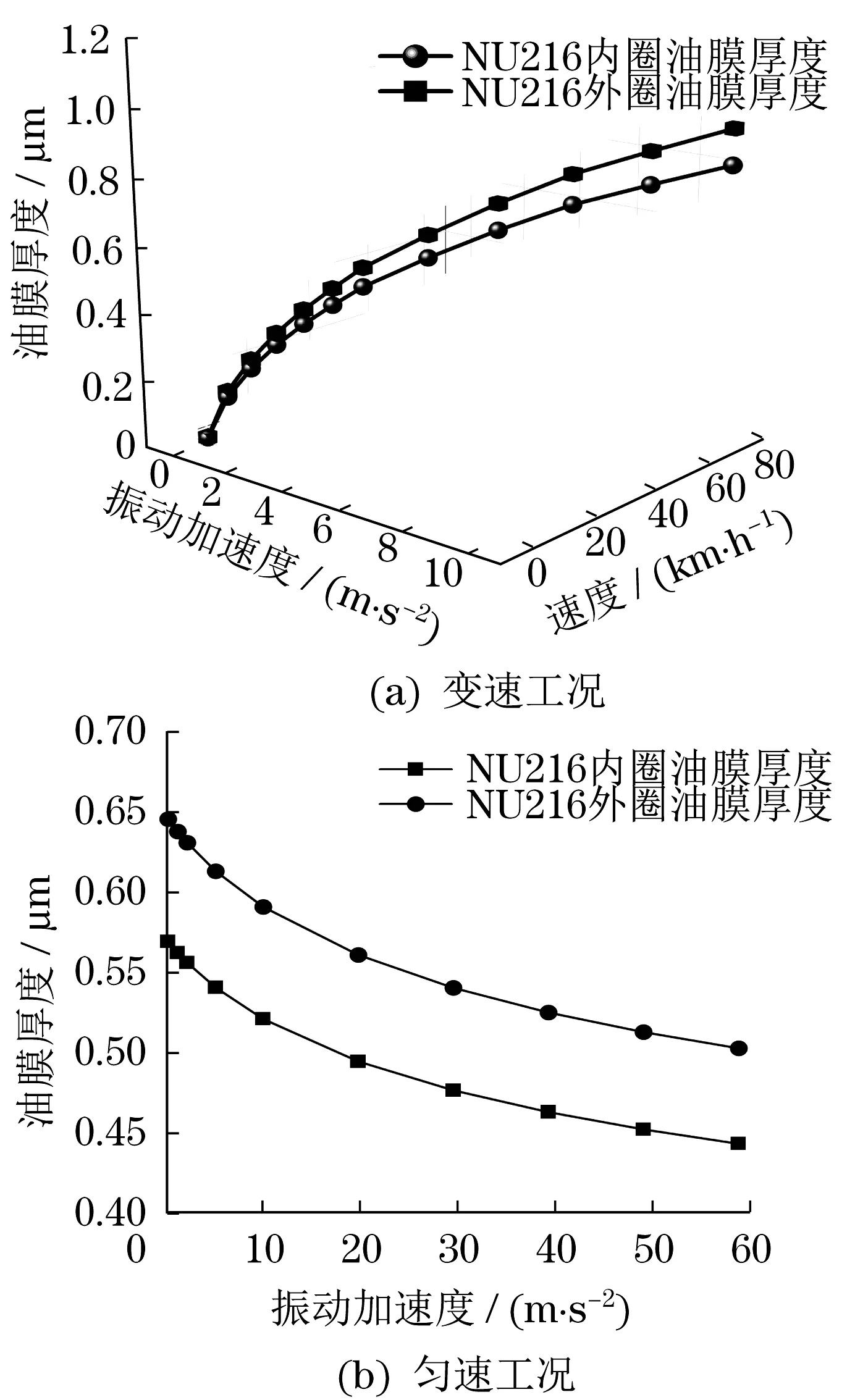
图7 不同振动工况轴承油膜厚度变化Fig.7 The change of bearing oil film thickness under different vibration conditions

图7表明，在变速工况下，随着车辆速度的增大，电机转速的提升使轴承润滑更充分，油膜厚度不断增加。而速度提升的同时也增大了电机的振动加速度与轴承动载荷，一定程度上抑制油膜厚度的增长，油膜厚度的增长逐步趋于平缓。同理，匀速工况的电机转速恒定，振动加速度从0 m/s2升至58.8 m/s2，轴承油膜厚度减小了约20%。

2.4 电机动载荷与轴承等效电容的关系

电机振动造成轴承赫兹接触面积与油膜厚度的变化，影响轴承电容的大小。结合以上参数计算结果以及轴承电容的计算公式，得到不同工况电机振动加速度与轴承电容的变化如图8所示。

从图8可知，在变速工况下，由于电机转速提高，增加的油膜厚度大于轴承动载荷提高对赫兹接触面积的影响，随着电机的转速与振动加速度的增大，电机轴电容逐步减小。在匀速工况下，电机转速不变，振动加速度的提高增大了轴承动载荷，使轴承的赫兹接触面积增大，油膜厚度减小，电机轴电容不断增大，动载荷与轴电容呈正比。

图8 不同振动工况的轴电容Fig.8 Bearingcapacitanceunderdifferent vibration conditions

3 动载荷对轴承电腐蚀参数的影响

3.1 动载荷对电机轴电压与轴电流的影响

根据电机的高频共模等效模型，搭建电机轴承电流集中参数Simulink仿真模型。在此模型中，轴电压的幅值一旦超过油膜的阈值电压，轴电容被切断，接上轴承电容击穿电阻，模拟不同的轴承电容与阈值电压参数下，电容发生击穿产生的轴电流与轴电压。一般润滑油的介电强度约为15 kV/mm。本文以15 kV/mm 作为轴承润滑微区的击穿场强Eth，油膜发生击穿的阈值电压为Uth，最小油膜厚度为hmin。利用公式Uth=Eth·hmin，计算不同工况下的轴承油膜击穿阈值电压。将不同工况下的轴电容及轴承油膜阈值电压参数代入仿真模型，得到轴电容击穿时电机振动加速度引起的轴承动载荷对轴电压与轴电流的变化如图9所示。

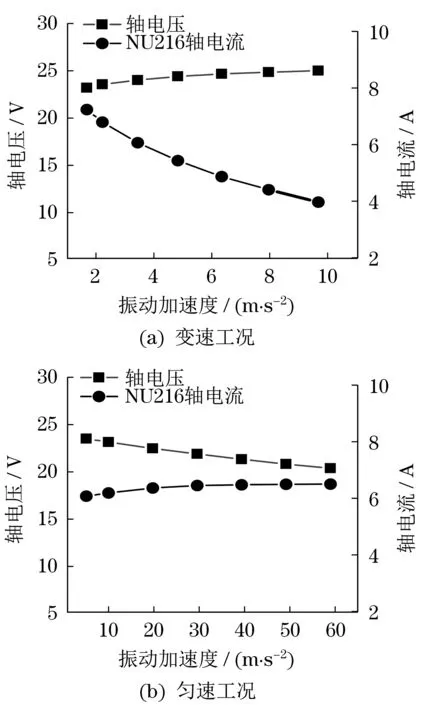
图9 不同振动工况下的轴电压与轴电流变化Fig.9 Bearing voltage and bearing current changes under different vibration conditions

由图9可知，在变速工况下，由于振动加速度的提高，使轴承动载荷增大，轴电容减小，油膜厚度增加，轴承油膜的阈值电压增大。根据轴承分压比，轴电容减小，轴承两端的电压增大。振动加速度从0 m/s2升至9.68 m/s2，轴电压提升约16%。此外，油膜阈值电压的提高减少了轴承电容的击穿，当达到一定转速，有可能不再发生油膜击穿。因此，振动加速度升至9.68 m/s2时，轴电流降低了近50%。同理，匀速工况下的振动加速度从0 mm/s2升至58.80 mm/s2，轴电容不断增大，轴电压降低了约15%。油膜击穿的阈值电压降低，增加轴承油膜击穿的概率，轴电流增加了约10%。

3.2 动载荷对电机轴电流密度的影响

为评估轴电流对轴承寿命的损害，需要确定轴承电流密度Apk的大小。轴电流的最大幅值为Iz，利用公式Apk=Iz/AH，计算得到不同工况振动加速度引起的动载荷对电机轴电流密度的影响，如图10所示。

图10表明，随着电机振动加速度的增加，2 种工况的轴电流密度都逐渐降低。轴电流密度主要受赫兹接触面积的影响，振动加速度与动载荷越低，轴承的赫兹接触面积越小，轴电流密度越高。对比2 种工况，振动加速度从0 m/s2升至10.0 m/s2，变速工况轴电流密度减少近50%，匀速工况轴电流密度减少约37.5%，变速工况下动载荷变化对轴电流密度的影响更大。文献［9］计算了轨道车辆电机轴承不同轴电流密度下的轴承的电气寿命。结果表明，轴承击穿时的轴电流密度越高，对轴承的腐蚀越强。轴电流密度每提高约0.5 A/mm2，轴承都将缩减近90%的电气寿命。车辆实际运行时，电机振动加速度普遍集中于0～9.8 m/s2的低动载荷范围，轴承油膜放电击穿的轴电流密度高于2.0 A/mm2，电机轴承油膜击穿产生的轴电流会对轴承电气寿命产生极大损害。

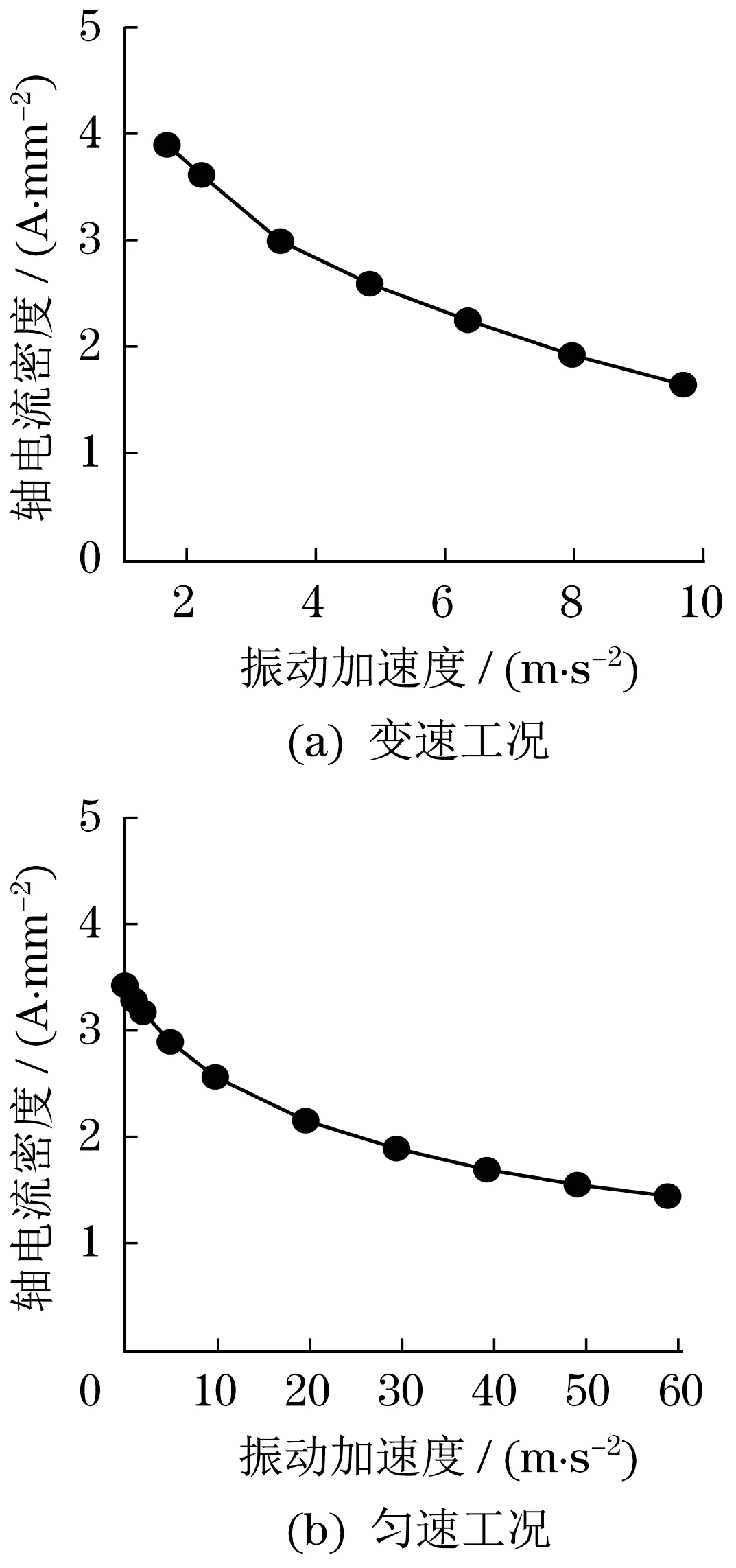
图10 不同振动工况下的轴电流密度变化Fig.10 Bearing current density changes under different vibration conditions

4 结论

（1）本文建立轨道不平顺激励下的轨道车辆振动模型，分析轨道不平顺对轨道车辆电机的时域振动效果。研究了电机轴承在不同振动工况下的动载荷对轴承滚动元件与滚道之间的油膜厚度和赫兹接触面积的影响，计算了地铁电机的轴承等效电容，探讨电机振动引起的电机动载荷与轴电容之间的关系。

（2）分析了轨道车辆在不同动载荷下轴承击穿的轴电压、轴电流与轴电流密度。结果表明，车辆实际运行时，电机振动加速度普遍集中于0～9.8 m/s2的低动载荷范围，轴承油膜击穿时的轴电流密度较高，电腐蚀会极大地损害电机轴承的电气寿命。