基于BP改进PID的掘进机闭环回路跟随误差联合仿真

杨文明，白建朋，黄 莹，李 峰，唐一飞

（1.郑州煤矿机械集团股份有限公司成套装备研究院，河南 郑州 450048；2.河南理工大学机械与动力工程学院，河南 焦作 454150）

掘进机被广泛应用于工程机械部件加工等领域，在道路快速挖掘、隧道施工方面发挥着重要功能，能适应更苛刻工况的使用要求［1-3］。通过利用PID 算法对推进参数进行了偏差修正，极大降低了协调性，在推进期间将会产生冲击甚至明显的振动现象，导致地层丧失稳定性［4-6］。赵浩林等［7］在PID算法中融合了神经网络方法，以此测试了推进系统参数控制性能，之后利用Matlab 中构建了仿真模型，通过测试发现上述融合算法能够获得优异的阶跃响应特性［8］。宋立业等［9］主要研究了隧道掘进机在推进过程中的运行速度与压力匹配状态，通过RBF 神经网络算法实现了速度与压力之间的良好匹配性能。以AMESim 和Matlab 进行联合仿真测试发现，采用上述控制器可以有效限制负载发生大幅扰动的情况，实现推进压力与速度之间的良好耦合状态，同时大幅降低了波动程度。李阁强等［10］针对复杂底层条件下的盾构工作过程进行了研究，为改善推进速度与压力控制效果，根据实际控制需求设计了通过BP 神经网络实现的控制策略。以Simulink 进行了仿真测试，结果发现，当其遇到沉降、撞击等突变负载时依然能够精确调控速度与压力，表现出了优异的稳定性。

本文从推进系统的工作原理层面出发，为系统构建了AMEsim模型，通过仿真测试获得系统速度与压力参数；通过Simulink算法构建BP神经网络控制器，同时以BP神经网络与PID方法进行联合控制，由此计算获得系统的压力与速度变化曲线。相对于PID控制方法，以BP神经网络和PID方法进行融合控制时，能够对压力与流量不恒定的系统获得更优控制效果。

1 推进系统设计及跟随误差模型

1.1 系统设计

为保证盾构系统保持准确掘进状态，同时获得更快挖掘速度并保持稳定掌子面，要求液压系统液压油缸达到同步协调控制的性能，因此将油缸设置成分组排布的结构［11］。本研究为推进系统配备了闭式变量柱塞泵，由于该泵进行输出时可以对最高压力进行限制，在压力上升到最大值时，将保持0流量状态来实现保压过程，从而获得节能。系统调速回路原理如图1所示，各个部分再运行控制过程可以实现相互协调的状态，共同达到流程调节的功能。

根据图1可知，推进油缸通过伺服阀进行速度调控，油缸运行的压力通过溢流阀进行控制，可以根据实际运行控制需求实现流量的精确调节。油液的流动方式为先经过伺服阀，再经过比例调速阀流入到油缸中，推进油缸利用撑靴对管片施加载荷，其中，撑靴可以确保油缸推力被均匀传输给管片，从而避免管片发生破损的问题；完成推进过程后再转换为管片拼装形式，原先对管片施加作用的推进油缸经换向阀完成缩回动作［12］。

图1 节流调速回路原理Fig.1 Schematic diagram of throttle speed regulating circuit

以闭环调节油缸压力与速度原理如图2所示。对油缸速度控制与压力控制方式相近，通过位移探测器收集到油缸在不同时刻下的位移数据，再将测试数据传输至控制器中，经对比运算获得各油缸的最大位移，以PID 算法将稳态性误差去除后再将其转换成调控比例调速阀的信号［13］。

图2 闭环控制原理Fig.2 Schematic diagram of closed-loop control

1.2 跟随误差

利用误差理论进行分析可以发现，当输入信号或者外部负载发生变化时，将会对系统的稳态性误差也产生明显影响［14-15］。其中，外负载与输入信号分别对应负载误差与跟随误差，本文通过仿真模型重点研究了误差引起的液压系统稳定性变化。

假定推进油缸保持一致的腔体压力，忽略油液泄漏产生的影响，同时认为油液保持层流状态，构建得到以下方程。

首先构建如下的压力平衡方程：

式中：p1、p2为无杆腔与有杆腔压力；A1、A2为油缸无杆腔与有杆腔有效面积；Bp为活塞与负载黏性比参数；mt为计算得到的油缸活塞和负载总质量；FL为总负载；Kf为负载弹簧刚度；xp为活塞位移；t为运行时间。

油缸的流量连续方程为

式中：pL、V2分别为油缸无杆腔流量、有杆腔有效体积；Cip为油缸泄漏系数；βe为液压油弹性模量。

通过拉氏变换方法处理式（1）与式（2）得到以下方程：

式中：QL、PL分别为无杆腔流量、油缸压力；Xp为无杆腔位移函数；S为液压固有频率；P1、P2分别为油缸无杆、有杆腔压力；G为油缸高压腔液液压固有频率；Ctp为阀芯位移传递系数；β为油缸高压腔液压油弹性模量。

比例调速阀流量qt计算式如下：

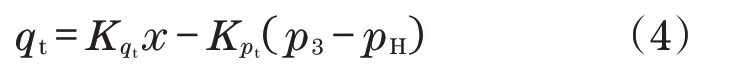
式中：Kqt为流量增益；Kpt为压力增益；x为阀芯位移；pH为负载压力；p3为调速阀的进口压力。

将式（5）通过拉氏变换得到流量函数为

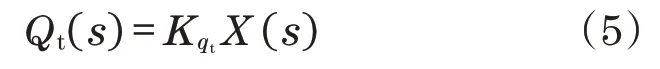
根据式（3）、式（4）与式（6）可以得到位移函数为

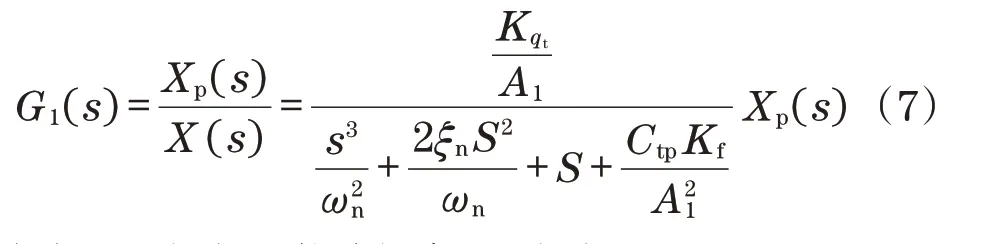
式中：ωn为液压激励频率；ξn为液压阻尼比

根据输出位移函数G1（s）构建得到的跟随误差反馈结果如图3所示。图中：X为输入位移信号；Xi为输入函数；Xp为输出函数。

图3 系统跟随误差反馈结构Fig.3 Structure diagram of system following error feedback

按照图3的处理方式完成拉氏转化获得以下结果：

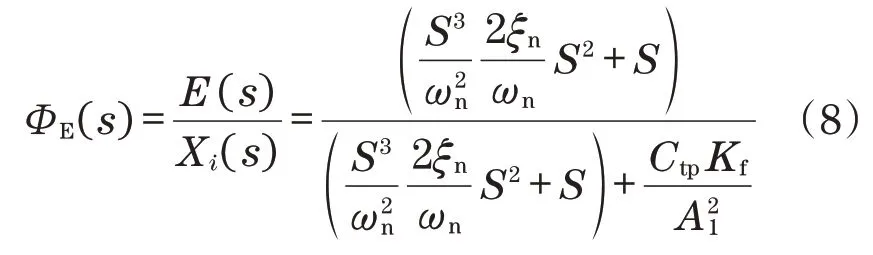
式中：G（s）为油缸活塞位移输出函数；H（s）为油缸活塞位移输出反馈函数；E（s）为跟随误差。

1.3 节能系统控制策略设计

本文同时采用液压与电气控制方式进行势能回收，利用调节液压马达排量的方式来达到控制动臂运动速度的功能，大幅降低程序设计难度，并且能够满足系统的远程控制需求。

具体控制策略如下：动臂受到重力与有杆腔液压油压力作用发生下降，此时蓄能器压力也不断提高，更多压力能被储存起来，引起动臂下降速度也不断变慢，满足控制过程的要求。在最初下降阶段，蓄能器保持较小压力，动臂下降速度不断加快，此时可以接入发电机使重力势能转化成电能并储存到超级电容中，由此实现对动臂速度的控制。

本文设计了一种根据流量调节方式实现的PID 控制方法，随着动臂逐渐下落后，在蓄能器中形成了更高压力，此时发电机也参与控制过程并引起系统压力的改变，提高了控制过程的复杂性，难以实现压力控制的功能。考虑到流量也会对动臂下落速度造成影响，通过调节变量马达排量的方式使其达到不同的转速。

2 控制器设计

PID控制器递进计算方程为

系统稳态误差ess计算方程为

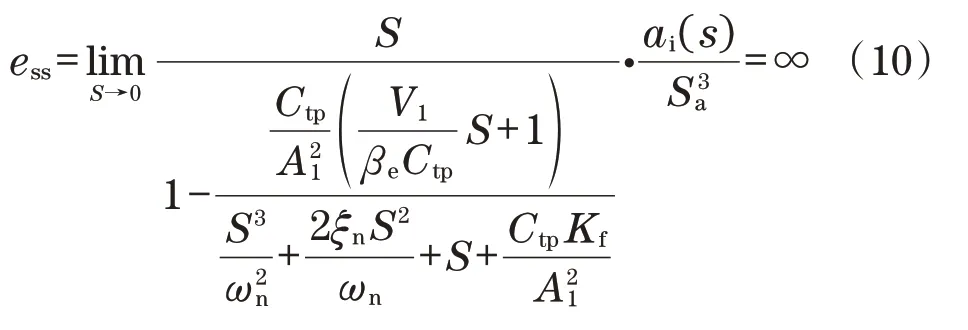
图4给出了本文设计的控制器结构。其中，PID 控制器程序通过C++程序进行编写得到，将油缸压力与流量作为控制器的输入，输出端是通过在线训练获得的输出信号u（k）以及其他参数。

图4 BP改进PID控制器原理Fig.4 Schematic diagram of BP improved PID controller

3 动态性能分析

通过仿真测试得到动臂节能系统曲线如图5所示。对图5进行分析可知：①油缸活塞进行伸出时能够达到的最快速度为0.33 m/s，缩回过程能够达到的最大速度为0.25 m/s；②动臂油缸活塞伸出阶段的油缸大腔与小腔压力分别为7.6、9.1 MPa，随着大腔压力提高至15.0 MPa时，剩余油液则通过载阀完成卸荷过程；③进入缩回阶段时，大腔与小腔中都形成了很低的压力，此时通过动臂自身重力以及负载的共同作用发生下降，2个腔体发挥不同的作用，其中，小腔压力可以发挥油液补充的效果，大腔形成背压作用，避免下降阶段出现冲击振动的情况。

图5 动态性能曲线Fig.5 Dynamic performance curves

4 联合仿真

以PID 方法构建的AMEsim 仿真模型进行测试，得到压力与速度曲线如图6和图7所示，以AMEsim、Simulink 进行联合仿真构建的模型获得了图6和图7所示的压力与速度曲线。通过对比发现，以PID 方法进行控制时，最初为50 mm/min 的油缸速度发生一段较长时间的振荡之后才达到了80 mm/min 的稳定值，之后在该速度下保持稳定状态；随着油缸压力的增大，逐渐接近24 MPa，期间发生了小幅波动，如图6所示。

图6 速度控制仿真结果Fig.6 Simulation results of speed control

图7 压力控制仿真结果Fig.7 Simulation results of pressure control

当选择AMEsim和Simulink方法进行联合仿真处理时，油缸可以快速达到80 mm/min的稳定值，此时速度也没有发生明显波动，如图7所示；并且油缸压力只经过很短的时间便升高到24 MPa，根据图7可知压力也几乎没有发生波动的现象。由此可见，采用BP改进PID方法对不稳定压力与流量变化具备更强的适应性。

5 结语

本文通过仿真模型重点研究了误差引起的液压系统稳定性变化，并给出了BP 改进PID 控制器控制设计。当选择AMEsim 和Simulink 方法进行联合仿真处理时，油缸可以快速达到80 mm/min的稳定值，此时速度也没有发生明显波动，压力也几乎没有发生波动的现象。综上，采用BP 改进PID方法具备更强的适应性。