氢气管道内部凸起对流场影响的数值模拟研究

吕 超，刘艳龙，陈绪鑫，殷宏鑫，孙铭赫

（东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004）

氢气作为能源，具有能量密度大、无毒无味无腐蚀、便于存储和运输及零碳排放的优点，因此具有很广阔的应用前景［1］。2019年3月，氢能首次被写进我国《政府工作报告》之中［2］，这表明我国对于氢能非常重视。氢能的有效利用，氢气的运输是重中之重，其中管道运输具有运载量大、效率高、经济效益高等优势，因此具有良好的市场前景［3］。

在氢气的管道运输中，如果管道内部有污染物堆积或管道存在较大的加工误差，则会造成管道内壁形成凸起。氢气管道内壁的粗糙程度对氢气的流场具有较大的影响，尤其是在直角弯管处，如果管道较为粗糙，就会加剧氢气输送的不稳定性，造成安全隐患，而管道内壁形成的凸起是造成管道内部粗糙程度高的重要原因之一，因此研究氢气管道内部凸起对流场的影响非常必要。在管道受损分析方面，单会娜［4］对管道产生缺陷的原因进行了分析与检测，提出不锈钢管道的焊缝表面易受到特定介质的腐蚀。Pluvinage［5］提出了利用缺口修正失效评估图对氢气管道缺陷进行评定的方法。赵博鑫等［6］对氢气管道的钢管和材料进行了适应性分析，指出管道焊缝内部有夹杂物等缺陷极易造成氢腐蚀而破坏管道。李强林等［7］对气体管道内部凹坑缺陷进行了分析与评价，分析了有关气体管道出现凹坑缺陷的原因。可见在气体输送管道方面，国内外均着重研究管道的缺陷问题，而对于管道内部凸起则研究较少，尤其是微小凸起对管道的影响的流场分析。从文献［7］可知，气体管道不仅会有凹坑缺陷，在表面也存在凸起，虽然这些凸起形状各异，但根据平滑程度大致近似于锥形、圆柱形以及圆柱与球冠的组合体等形状。本文运用Fluent 模拟氢气流动时管道内壁不同形状的凸起对管内流场的影响。

1 模型建立

1.1 整体物理模型

以欧洲大规模使用的氢气管道为研究对象，结合我国实际情况，设计氢气管道的尺寸为：管道直径600 mm，直角弯管两边接口的直线管道长度均为6 000 mm，呈90°分布，其中心截面均在z=0平面上，3种凸起均位于直角弯管凸侧内壁。运用SCDM软件进行建模，z=0的直角弯管二维截面如图1所示。

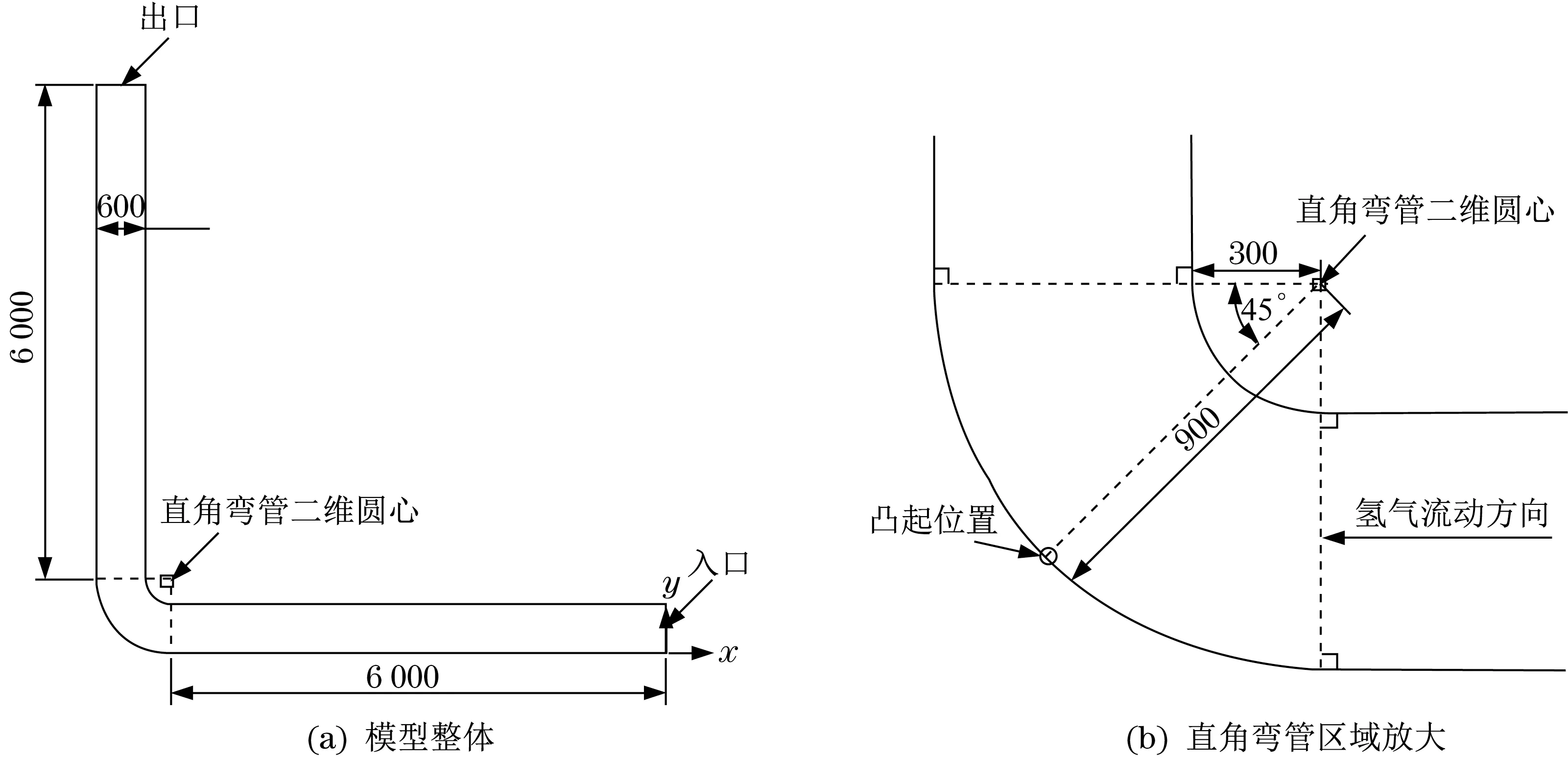
图1 z=0的直角管道二维截面Fig.1 Two-dimensional section diagram of right angle pipe with z=0

1.2 凸起处的微小模型

3 种典型凸起均为对称形状，其对称轴均通过直角弯管圆心。凸起的二维截面如图2所示。凸起的底部宽度均为18 mm，最大高度为11.95 mm，且在管壁的同一位置，均对称于同一对称轴。数字1、2、3、4、5、6、7代表的直线是本次研究使用Fluent模拟设定的监测线，将它们分别命名为监测线1～监测线7。在数字8 代表的曲线上按照等距原则设定20 个监测点。利用这些监测线、监测点获取凸起上各点的压力值和速度大小。

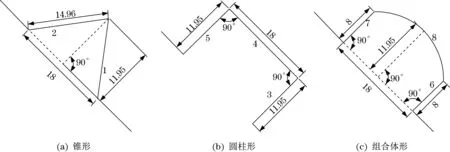
图2 典型凸起的二维截面Fig.2 Two-dimensional cross-section diagram of typical bulges

2 网格划分及模拟参数设置

2.1 网格划分

为减少计算量，提高计算精度，对原来的几何模型进行简化，取原始管道模型的中轴面建立二维管道模型。在划分网格时采用四边形的结构化网格划分方法，划分完成过后将其转化为非结构网格导入Fluent求解器进行计算。

利用ICEM 所划分出的网格（取凸起附近的一部分管道示意）如图3所示。图3（a）的网格数量约为65万，图3（b）和图3（c）网格数量约为70万，经检验网格质量均在0～1 之间且平均网格质量在0.9以上。

图3 几何模型的结构化网格划分Fig.3 Structured mesh division of geometric model

2.2 模拟参数设置

2.2.1 假设条件

忽略氢气流动对管道几何尺寸造成的微变、氢气流过凸起表面及其附近对管道内的温度变化、氢气管道内的密度变化、氢气管道内的壁厚。

2.2.2 模拟参数设置

本次模拟的氢气流速为8 m/s，在圆形管内流动，特征长度L取圆管的直径d。推导得圆管内流动的雷诺数计算公式为［8］

式中：V为截面氢气的平均速度；v为流体的运动黏度。

氢气的运动黏度为241×10-6m2/s，圆管直径为0.6 m，代入式（1）得出氢气流动的雷诺数Re=19 917＞2 320，管道内的风流状态为湍流。因此选择标准k-ε模型计算流体，常数取值见表1。压力-速度耦合算法选择SIMPLE算法。

表1 标准k-ε特定常数取值Tab.1 Standard k-ε specific constant values

氢气管道中的温度为300 K，Fluent 初始气压为1.013 25 kPa，其他参数设置见表2。

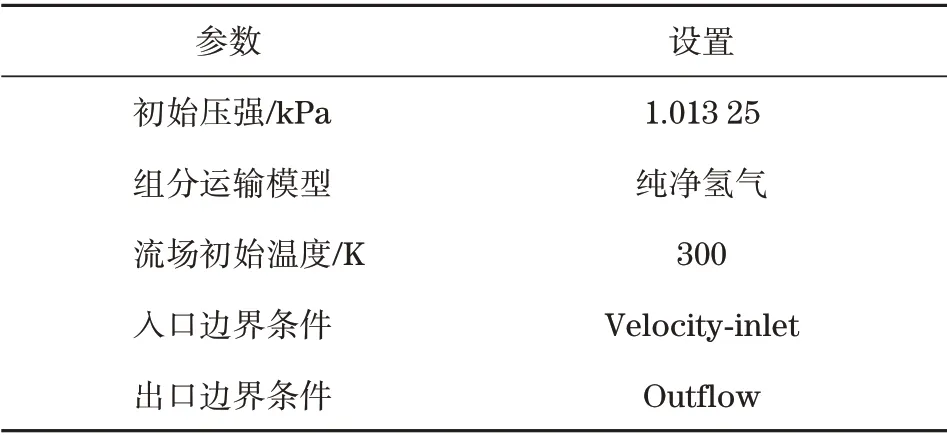
表2 Fluent模型主要参数设置Tab.2 Main parameter settings of Fluent model

3 结果与讨论

3.1 压力分布

直角管道凸起处的压力大小与分布影响管道的强度和使用寿命，某部分压力过大或者分布不均可能会造成细微裂缝，严重影响输送安全。因此对凸起表面压力分布进行了模拟仿真，氢气管道直角弯管凸起处的压力分布云图如图4所示。

根据模拟过程中凸起不同位置（Y坐标值）的压力的变化，绘制变化曲线，如图5所示。

分析图4和图5可以得出结论：凸起附近较大的压力场均在右侧靠近监测线的区域，且锥形凸起附近的压力峰值最大，圆柱形凸起和组合体凸起的压力峰值几乎相等。随着纵坐标的增大，凸起左侧轮廓线压力逐渐增大，但压力普遍较小，且均为负压，凸起右侧轮廓线上压力会先上升然后骤降，使得此曲线的上顶点处附近压力值较小，监测线3 的平均压力最小，圆柱形凸起顶部压力先下降而后突然上升，然后趋于稳定，曲线8 上压力值大小呈现出抛物线形式的变化，开口向上，压力先降后升，且曲线末端（纵坐标最大位置）压力值小于始端。

图4 直角弯管凸起附近压力分布Fig.4 Pressure distribution near the bulges of right-angle bend pipe

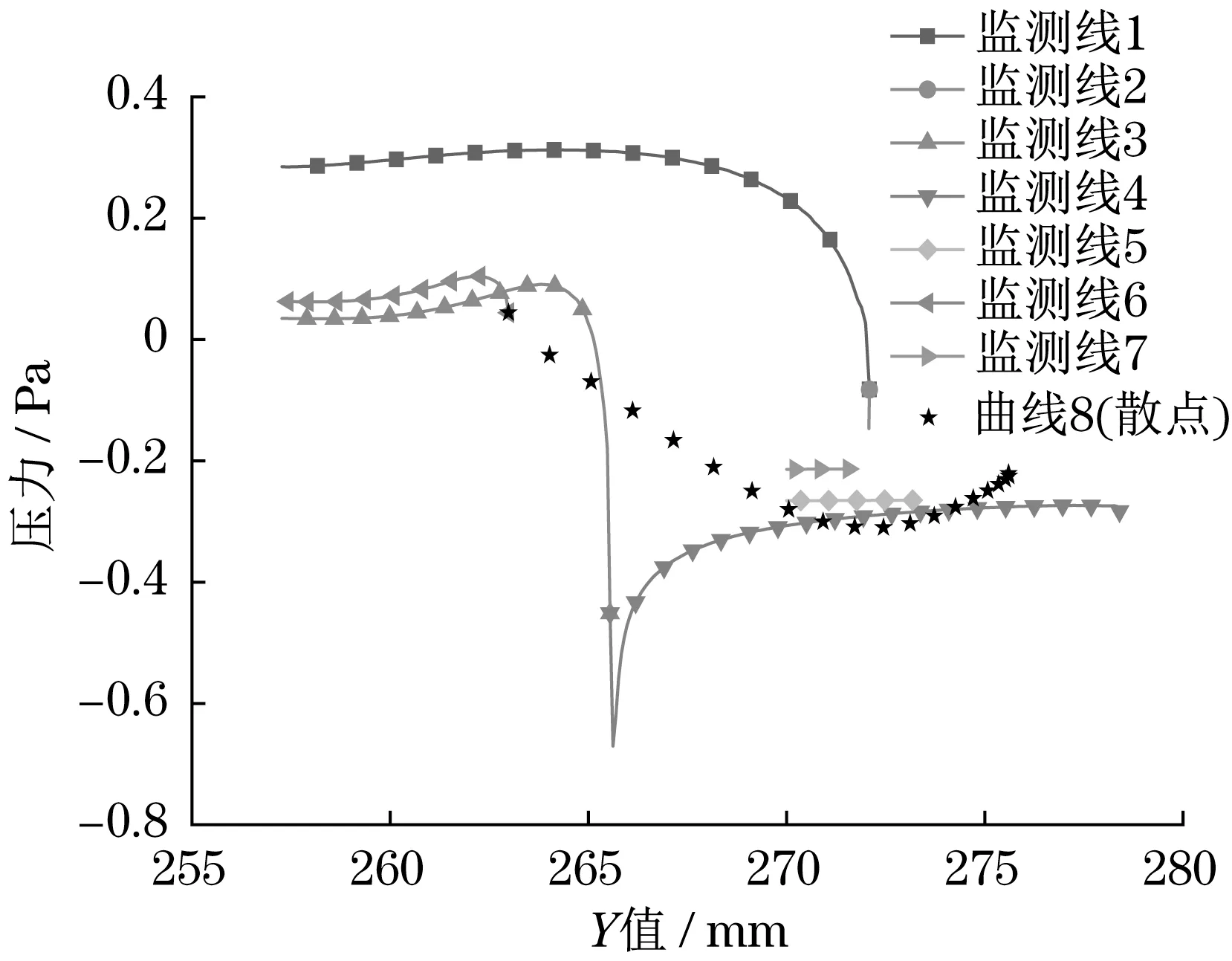
图5 3种凸起不同监测位置的压力变化Fig.5 Pressure changes at different monitoring positions of three bulges

3.2 速度分布

气体对凸起表面的冲击也是必须要考虑的因素，这涉及氢气流动时的稳定性，能直接反映冲击情况的便是速度大小分布与方向，管道直角弯管处内壁凸起附近气体流速云图如图6所示。气体速度分布情况如图7所示。

分析图6和图7可知：凸起表面的氢气流动速度均非常低，且在凸起左右两侧靠近管壁处形成低速区域，背风侧形成速度死区，组合体形凸起速度死区最小；氢气流动方向一开始平行于管壁，后逐渐变化，到锥形凸起顶点或圆柱体凸起和组合体凸起右侧顶点时与管壁大约呈60°夹角，随着继续流动又逐渐平行于管壁。

图6 直角弯管凸起附近速度分布Fig.6 Velocity distribution near the bulges of right-angle bend pipe

图7 凸起附近速度矢量分布Fig.7 Distribution of velocity vector near bulges

3.3 剪切力分布

剪切力的大小体现了流体对管道内部的冲击情况，本文根据模拟过程中凸起不同位置对剪切力变化的影响，绘制了变化曲线，如图8所示。

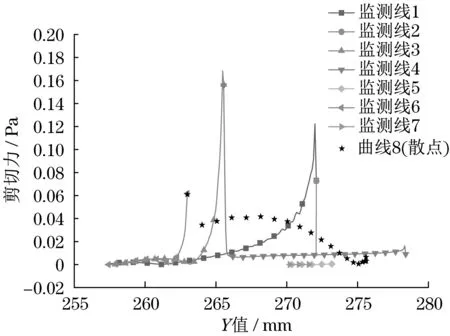
图8 3种凸起不同监测位置的剪切力变化Fig.8 Shear force changes at different monitoring positions of the three bulges

分析图8可知，凸起迎风侧剪切力变化规律是：自下向上剪切力逐渐增大，在中上段骤增，使迎风侧顶点处剪切力较大；圆柱形凸起顶部随着Y坐标的增大，剪切力最初骤降，后趋于平缓；而较为平缓的组合体凸起顶部曲面上，剪切力随着纵坐标的增大呈波浪式变化，总体是下降趋势，变化的剧烈程度较小。

4 结论

（1）锥形凸起相较于其他2种凸起压力峰值最大，圆柱形凸起压力峰值最低；凸起迎风侧附近区域形成较大的压力场，迎风侧顶部压力较小；凸起曲面顶部压力无突变现象，斜平面顶部压力先突变后趋于平缓；凸起背风侧压力随着位置改变变化不明显。

（2）3 种凸起表面相近区域氢气流动速度差几乎相同，凸起表面氢气流动速度较低并在凸起两侧形成低速区域，背风侧区域面积较大，形成速度死区，组合体形凸起速度死区最小；氢气流过时速度方向与管壁之间的夹角变化是从0°到约60°再到0°。

（3）剪切力分析结果表明：氢气对迎风侧顶部冲击较大，其他段无明显变化，组合体形凸起相对于其他2 种凸起剪切力峰值较小，流体对其冲击力度较小；顶部形状变化越平缓，流体对其冲击越平稳；背风侧几乎无冲击。

（4）圆柱形凸起压力峰值小，而迎风侧顶部受到的冲击较大，使得其对氢气流动阻碍作用较小而且容易被流体冲蚀，使凸起形状发生改变，更有利于流体流动，产生良性循环。