曲面微槽在螺旋槽动压径向空气轴承中应用的数值研究

董志强，王洪涛

（太原科技大学机械工程学院，山西 太原 030024）

由于螺旋槽动压径向空气轴承相对于一般构型动压空气轴承在承载力方面有明显优势，被广泛关注和研究［1-7］。由于计算流体动力学（computational fluid dynamics，CFD）技术的计算精度和效率大大提高，通过数值模拟设计研究空气轴承，相对于解析解和实验法能大幅降低成本［8-9］，提高性能。Renn 等［10］、Gao 等［11］都通过采用CFD软件取得了一定的研究成果；Al-Bender［12］通过谐振扰动形式对静压轴承的动态特性进行了分析；Lee 等［13］对气体轴承的静态特性以及动态特性进行了深入的探究；许怀绵等［14］对箔片轴承的变形问题进行了探究；戚社苗等［15］通过偏导数法，获得了扰动频率对气体轴承的影响规律；马纲等［16］对柱面气膜密封的结构参数设计进行了探究。

通过对文献的分析调研，在空气轴承结构参数对轴承承载力和稳定性的影响方面研究报道较多，鉴于精雕机曲面加工微槽道的能力越来越来强，使曲面曲边微槽代替传统的直面直边微槽成为可能。本文对气体轴承槽型结构进行了改进，用曲面槽代替直面槽，改进螺旋槽空气轴承微槽道，通过CFD流体动力学仿真，对构型改进前后的轴承参数影响进行了分析。

1 物理模型与计算方法

1.1 物理模型的建立

物理模型的建立如下：槽的形状由槽宽比、槽深比、槽长比以及槽角确定。其中，β为槽角，h为偏心距离。

式中：a为槽宽比；Γ为槽深比；为槽长比，ag为槽宽；ar为脊宽；cg为槽处轴承间隙；cr为脊处轴承间隙；lg为轴向槽全长；L为轴承长度。

改进后的槽型有了一定的弧度。图1为螺旋槽动压径向空气轴承结构简图。螺旋槽动压径向空气轴承几何参数见表1。

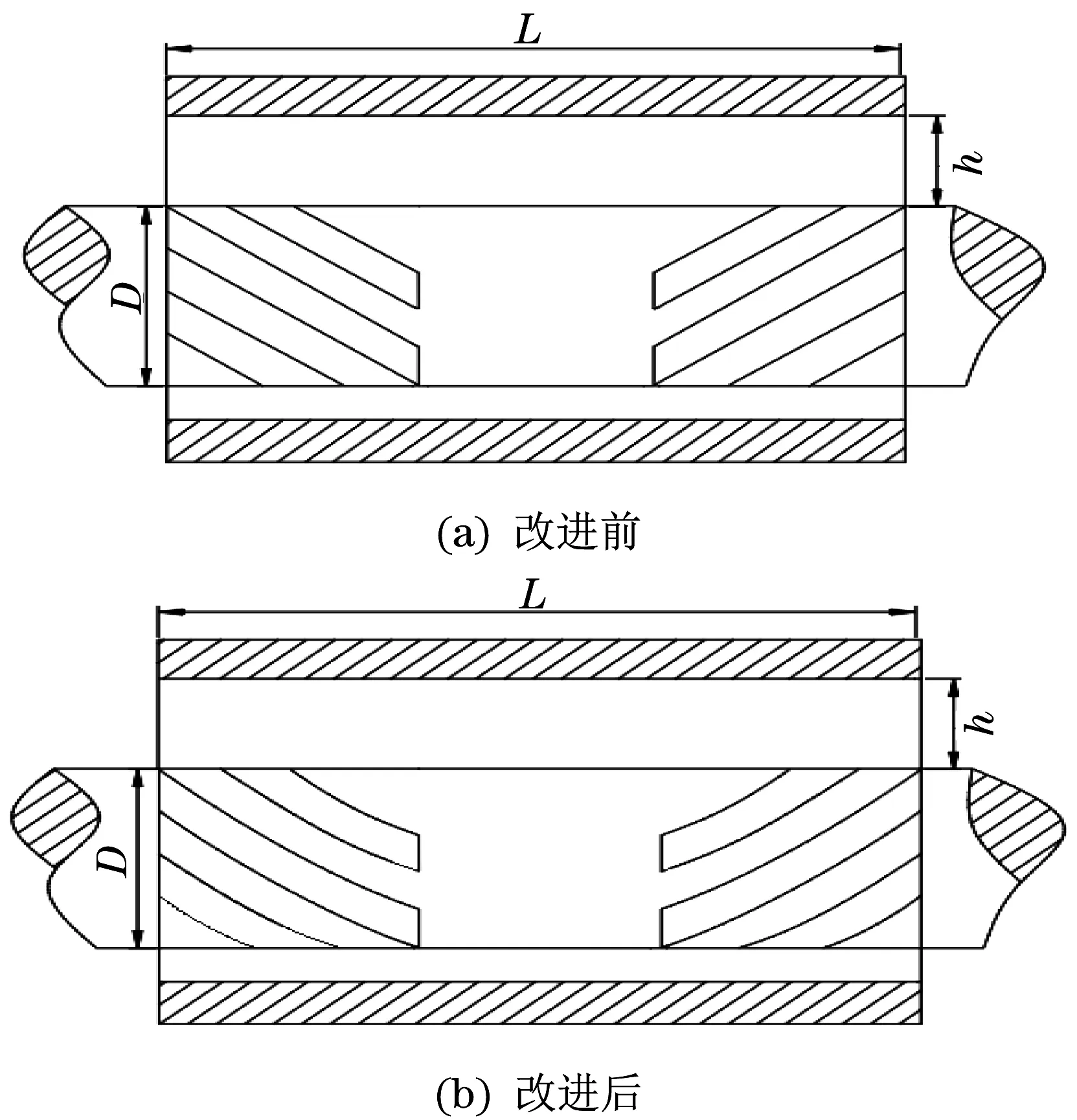
图1 螺旋槽动压径向空气轴承结构简图Fig.1 Working face expansion and structure diagram of spiral groove dynamic pressure radial air bearing

表1 螺旋槽动压径向空气轴承几何参数Tab.1 Geometric parameters of spiral groove dynamic pressure radial air bearing

2.2 纳维-斯托克斯方程

流体动力学仿真基于纳维-斯托克斯方程：

螺旋槽径向空气动压轴承承载力为

式中：wx为光滑轴承的承载力，N；wy为槽作用引起承载力的增量，N；G为螺旋槽结构系数；ε为偏心率；pa为环境压力，Pa；-z=Lg/L为槽长比；S=πDL为轴承面积，mm2；λ=L/D为长径比；Λ为可压缩系数。

螺旋槽结构系数：

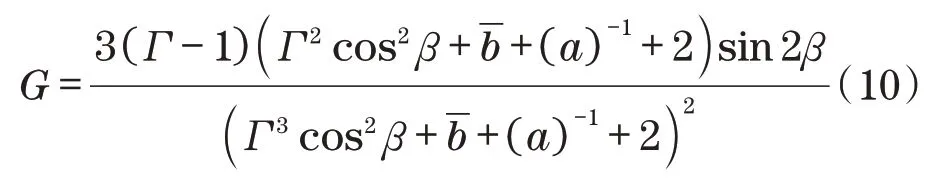
式中：Γ=cg/cr为槽深比；=ag/(ag+ar)为槽宽比，ag、ar分别为槽宽和台宽；β为槽角。

螺旋槽动压气体径向轴承总承载力为

2.3 气膜的建立

在SolidWorks 建立螺旋槽动压空气模型，再导入ANSYS 中，通过对空气流域进行抽取，得到了气膜流场区域，如图2所示。

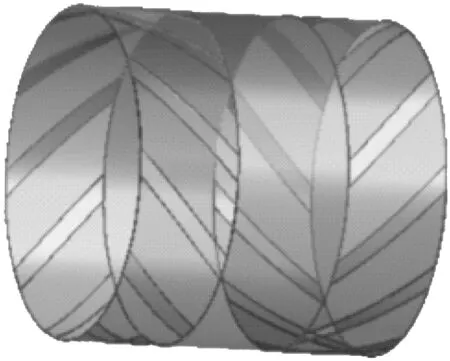
图2 气膜流场区域Fig.2 Gas film flow field area

2.4 气膜流域网格

由于轴承是偏心结构，不能利用对称性划分网格，所以对螺旋槽空气轴承进行整体区域划分。因为气体流场区域的复杂性，考虑到画网格时的方便性，本文运用ANSYS 中的mesh 进行划分，将槽区和台区通过前处理软件进行拆解划分网格，先整体划分网格，再分区精画，最后分层，经过多次尝试，得到气膜网格，如图3所示。整体网格质量经检测能够满足仿真要求。

图3 气膜流域网格Fig.3 Gas film watershed grid

2.5 边界条件的设置

空气轴承的两端分别为空气的压力进出口，为1个大气压，轴承的外壁面设置为轴承的固定壁面，内壁面设置为轴承的旋转壁面。速度为主轴的旋转速度。

2.6 网格无关性验证

根据数值收敛性分析，网格越多网格尺度越小，数值计算结果精度越高。当网格尺度减小到一定程度，计算精度趋于收敛，计算结果与网格尺度关联度消失。网格无关性验证结果如图4所示。随着网格数量的增加，承载力趋于平稳，综合考虑计算成本和收敛性分析，选取网格均布，数量为872 000个。

图4 网格独立性验证参数对比Fig.4 Comparison of grid independence verification parameters

3 计算结果与讨论

3.1 轴承构型改进前运行工况参数的影响分析

对轴承构型改进前进行气动力学分析，设置计算算例研究了空气轴承的转速n、偏心率ε、槽长、槽数对径向轴承中心面压力的影响。图5为数值计算对应径向轴承合理的压力场分布云图；图6、图7、图8和图9计算分析了不同工况参数下径向轴承的压力截面分布。随着偏心率和转速的增大，压力最大区呈现增大趋势，而压力最小区呈现最小趋势，且变化明显，说明轴承承载力受偏心率和转速的影响较大。同时观察到，压力曲线形状是相同的，但大小不同，压力最大区位置和压力最小区位置是相同的，符合轴承理论气膜压力分布，和文献计算结果吻合，验证了数值模型的正确性。

图5 轴承中心面压力场云图Fig.5 Pressure field cloud of bearing center surface

图6 轴承中心面压力曲线Fig.6 Pressure curve of bearing center surface

图7 轴承中心面压力曲线Fig.7 Pressure curve of bearing center surface

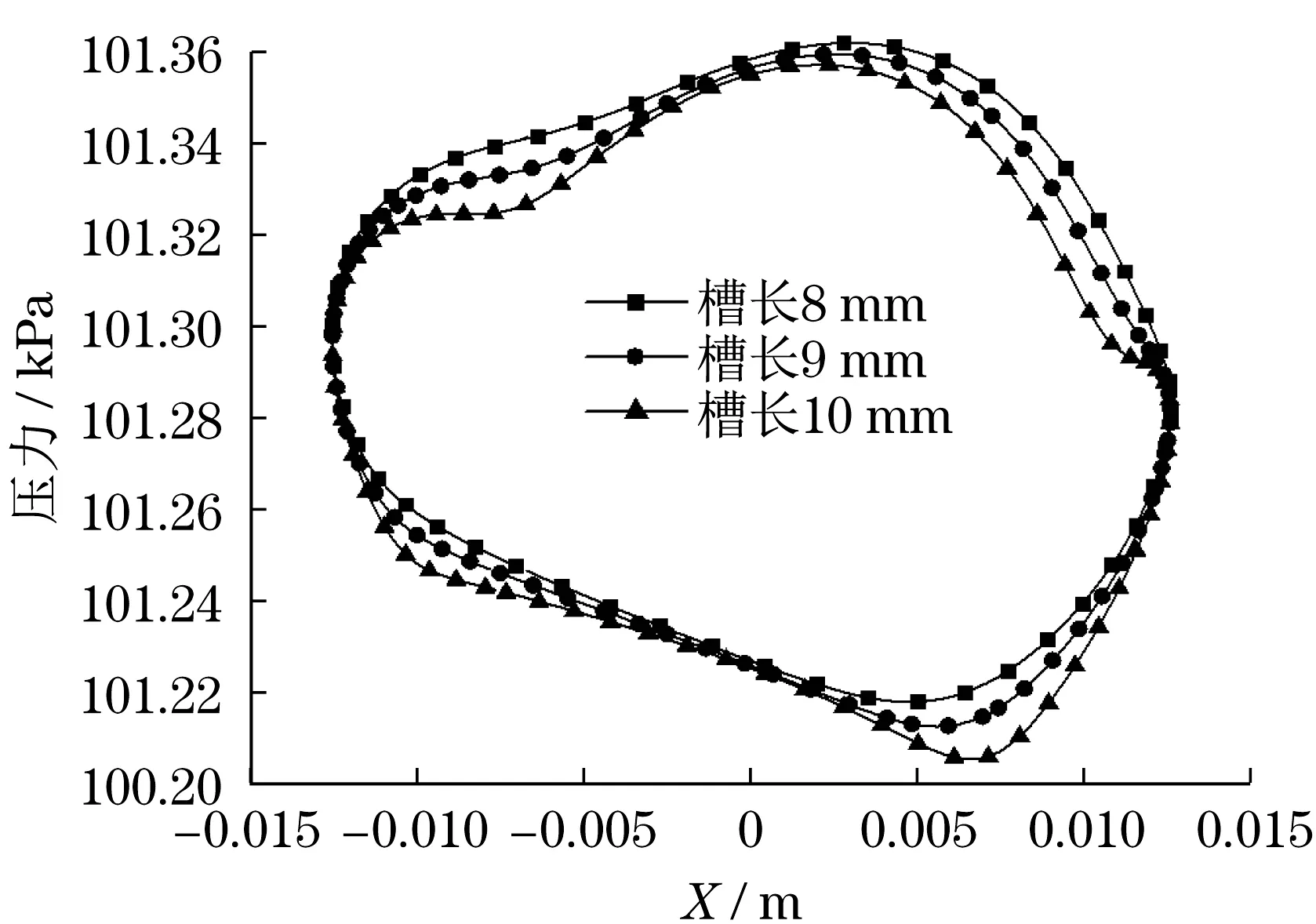
图8 轴承中心面压力曲线Fig.8 Pressure curves of bearing center surface

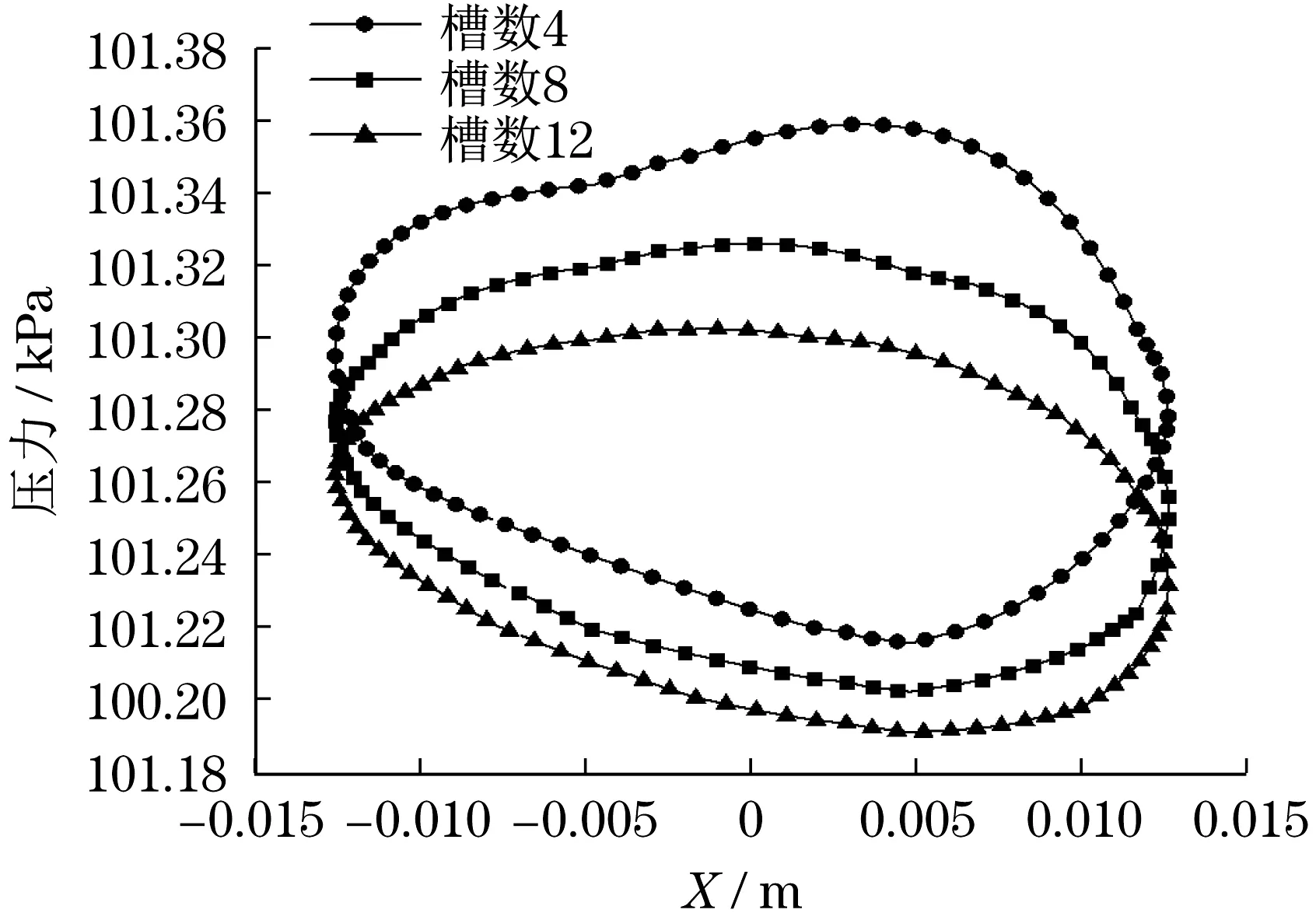
图9 不同槽数时轴承中心面压力曲线Fig.9 Pressure curve of bearing center surface

3.2 轴承构型改进后随工况参数影响变化的对比分析

为研究螺旋槽轴承构型改进前后不同工况参数对承载特性影响的差异性，根据槽深、槽宽、气膜、转速、构型差异，设置不同的轴承计算模型，得到槽深、槽宽、气膜、转速和构型与承载力之间的影响关系如下。

由图10可知，当转速一定时，随着槽深的增大，承载力随之变大。由于空气流经螺旋槽所经过的横截面积在增大，导致空气流经螺旋槽时所产生的阻力也在增大，动压效应也随之增强，承载力增加。改变槽型结构后，随着转速的增加，承载力相对于改进前明显增加。

图10 不同转速下承载力随槽深的变化Fig.10 Variation of bearing capacity with groove depth at different rotational speeds

由图11可知，随着槽宽的增长，承载力也在增加，进入螺旋槽的空气流量增多，使动压效应增强。改进螺旋槽轴承构型后，承载力随着槽宽的增长先增加随后减小，最后呈现上涨的趋势，但还是较之前结果有一些改善。

图11 不同转速下承载力随槽宽的变化Fig.11 Variation of bearing capacity with number of slots at different rotational speeds

由图12可知，当转速一定时，随着气膜间隙的增大，承载力呈现非线性减小，气膜间隙一定时，随着转速的增大，承载力增大。改进螺旋槽后，承载力明显增加。

图12 不同转速下承载力随气膜间隙的变化Fig.12 Variation of bearing capacity with air film clearance at different rotational speeds

4 结论

本文通过对螺旋槽空气动压径向轴承的研究，得出以下结论：①虚拟设计曲面螺旋槽微槽道，应用CFD数值仿真，通过对其在不同轴承参数下的性能进行比较分析，证明了曲边界在螺旋槽微槽道的应用具有可行性。②增加槽深、槽宽能提高轴承的承载力，增加气膜厚度，承载力呈现非线性减小。增加转速，也可使轴承的承载力增加，但可能会使轴承的工作系统不稳定，研究表明曲面槽和直面槽受轴承参数影响特性一致。本研究可为空气轴承的构型改进提供参考。