表面织构动压滑动轴承油膜力解析模型*

(1.河南科技大学机电工程学院 河南洛阳 471003；2.洛阳铁路信息工程学校 河南洛阳 471934； 3.国家轴承质量监督检验中心 河南洛阳 471003)

旋转机械是当今社会应用最普遍的机械设备，例如：电动机、航空发动机、叶片叶轮等。随着社会发展和人类的进步，旋转机械也向着重载高速、轻量化、大跨度、柔性强的方向发展[1]。旋转机械设备的核心零部件是轴承-转子系统，该系统具有明显的非线性。由于非线性现象对旋转机械的安全运行和生产，造成了重大安全隐患。因此，随着研究的深入，该系统转子间的非线性油膜力的影响愈发受到重视。

对非线性油膜力的研究，通常基于Reynolds方程解析油膜力，解析方法包括有限元法或有限差分法(Finite Difference Method，FDM)[2]、简化模型法、变分法[3]以及数据库法。然而，有限元法或FDM虽然计算结果准确性高，但计算速度慢且耗时；简化模型法虽计算精度低，但速度快，求解方法简单；变分法虽计算精度高，但编程不易且迭代次数多；数据库法具有高效和可靠等特点，但建数据库较为复杂，普遍应用性较差。以上求解方法各有优劣，为此国内外学者探讨了建立一种快速、高精度的解析模型，来求解轴承-转子系统的非线性油膜力。为了在不同边界条件下尽可能准确地求解Reynolds方程[4]，从而得到能够适用于非线性动力学的非线性油膜力，文献[5-6]提出一种油膜力计算方法，分析了油膜力的内部规律和特性；文献[7]基于动态“π”油膜假设模型，采用分离变量的方法对油膜力进行了解析；文献[8]提出一种结构简单、实用性强的油膜力解析模型；文献[9]通过二维变分不等式降阶的方法，对油膜力进行了解析。日前，研究人员虽然对轴承的油膜力做了一些研究，但对表面织构动压滑动轴承油膜力解析模型的研究却鲜有报道。

本文作者基于Sommerfeld边界条件推导了表面织构动压滑动轴承油膜力解析式，求解了不同织构参数下、不同织构区域量纲一油膜力，通过与其他模型在不同长径比和偏心率下的计算结果进行对比，验证了提出方法的正确性和有效性。

1 表面织构动压滑动轴承油膜压力理论模型

1.1 Reynolds控制方程

流体润滑的基础是Reynolds方程，解析该方程比较复杂，一般情况下需要简化该方程以便解析。根据相关假设，适合表面织构动压滑动轴承的Reynolds方程为

(1)

式中：μ为油液动力黏度，Pa·s；h为油膜厚度，m；p为油膜压力，Pa；Ω为轴转速，m/s；z为轴承长度方向坐标，m；θ为轴承周向坐标，m。

1.2 表面织构动压轴承油膜方程推导

表面织构动压轴承油膜理论模型示意图，如图1所示。

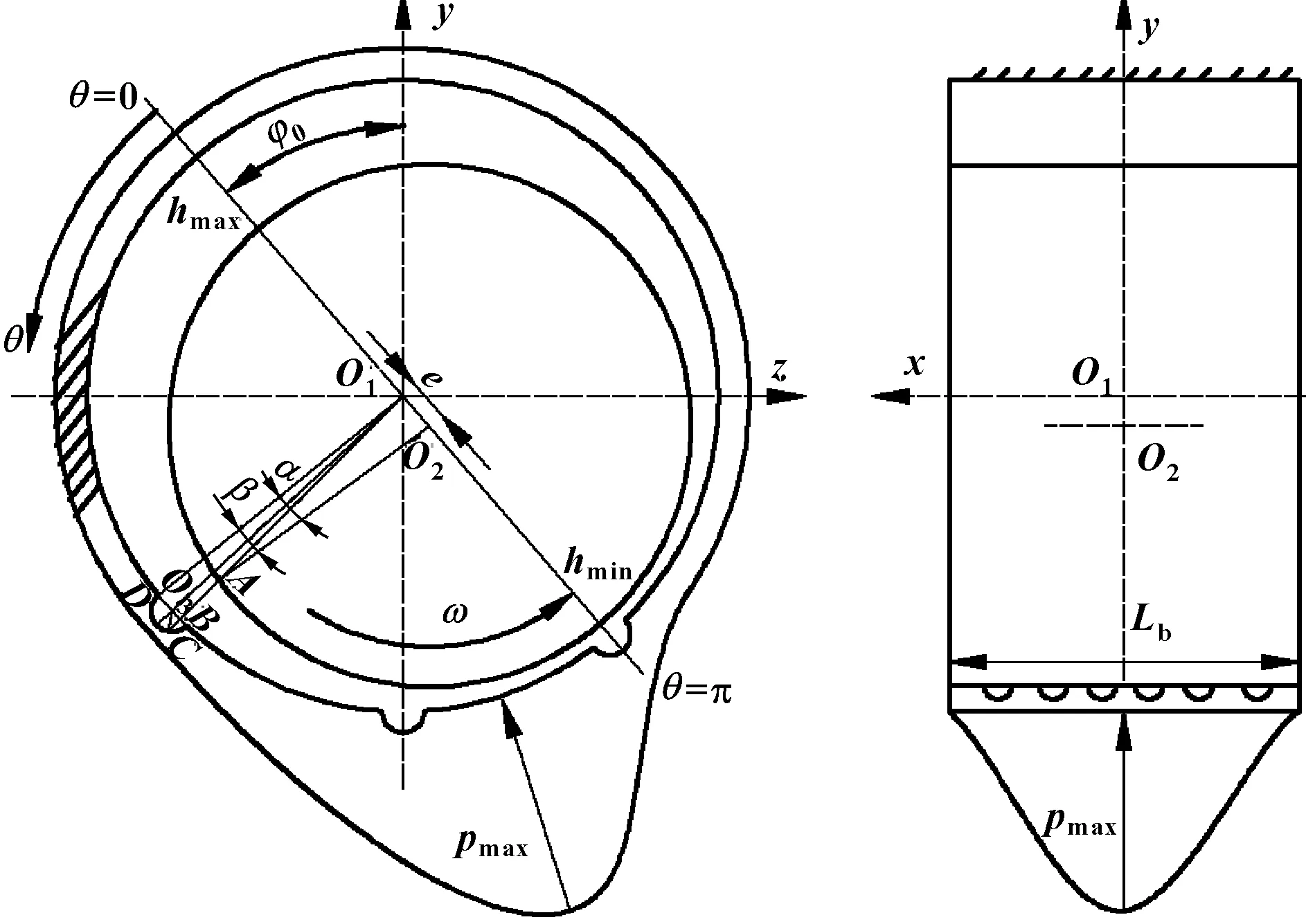
图1 表面织构滑动轴承示意图

光滑轴承油膜厚度为h1，油膜间隙c=R1-R2。则光滑轴承的油膜厚度表示如下：

h1=c+ecosθ

(2)

式中：e为轴承偏心距；c为轴承间隙。

在图1所示的表面织构动压滑动轴承示意图中，BC表示圆形凹坑的油膜厚度h2，且BC=O1C-O1B。故，织构化动压轴承油膜厚度表示如下：

h3=h1+h2

(3)

表面织构轴承中任意一个凹坑织构的油膜厚度h2为

(4)

因此，表面织构轴承油膜厚度h4为

(5)

表面织构轴承油膜厚度解析式对于大尺寸凹坑织构的计算具有指导意义[10]。表面织构轴承的微凹坑织构一般比较小，推导的油膜厚度解析式用于计算往往不够准确，因此进行一定程度的修正是必要的，使理论结果满足工程实际的需求。文中提出一种油膜厚度的计算方法——等体积法，对油膜厚度解析式进行修正。选择任意某一织构处的凹坑进行分析，表面织构轴承凹坑织构局部区域示意图，如图2所示。

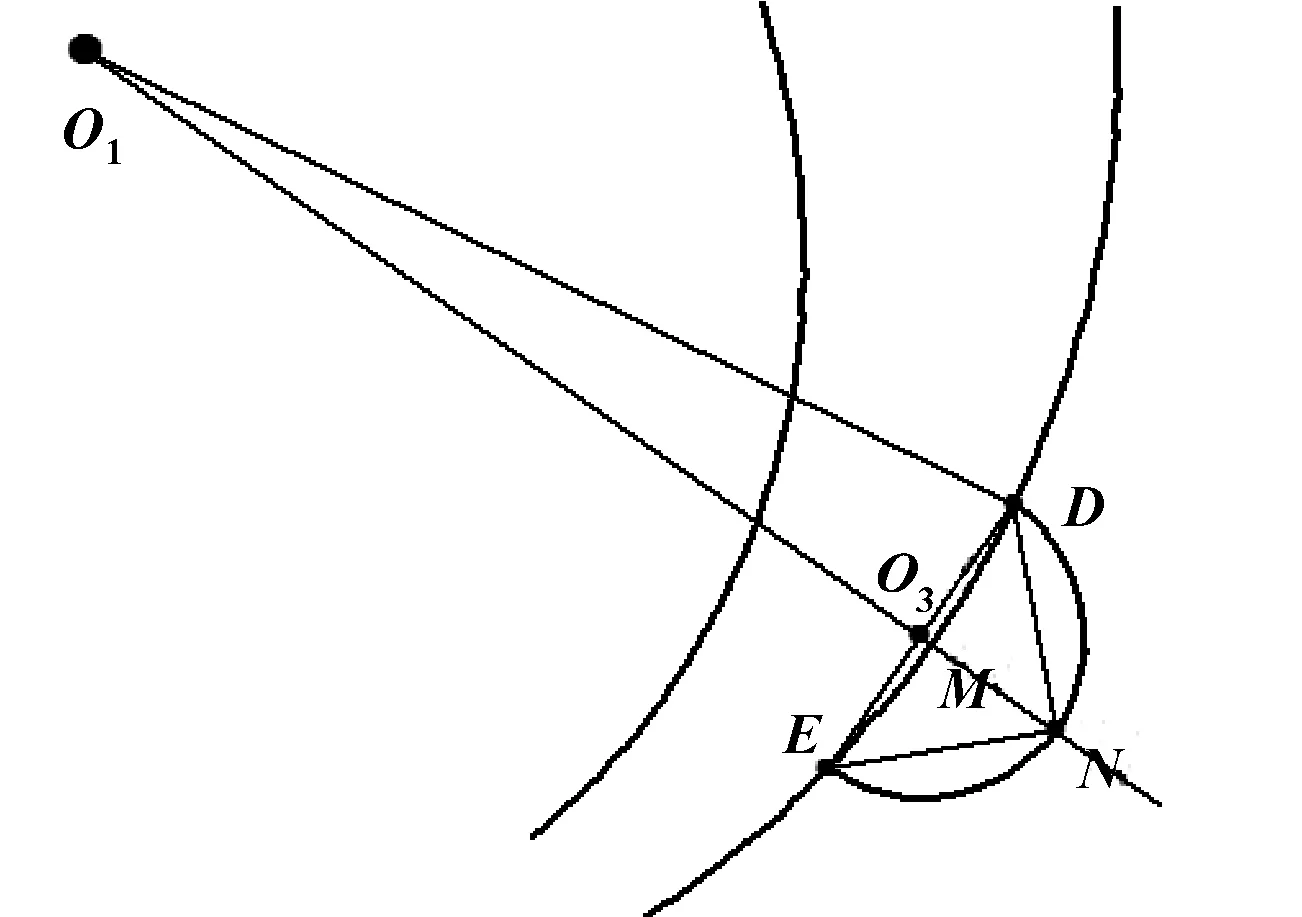
图2 表面织构轴承局部区域示意图

在图2中，有以下几何关系：

(6)

(7)

根据等体积法，则V球=V圆柱。在图2中，表面织构轴承微凹坑油液的油膜体积VEMDN表示如下：

VEMDN=VENDO3-VEMDO3

(8)

半球体体积表达式如下：

(9)

故，半球体体积VEMDO3为

VEMDO3=

(10)

将式(9)、(10)代入式(8)则表面织构轴承任意微凹坑增加的油膜体积为

(11)

令R1/R3=k，则式(11)圆形凹坑增加的油膜厚度表达式为

(12)

经过修正后，织构化动压滑动轴承的油膜厚度解析式如下：

(13)

光滑轴承油膜厚度与织构轴承油膜厚度的三维分布，如图3所示。

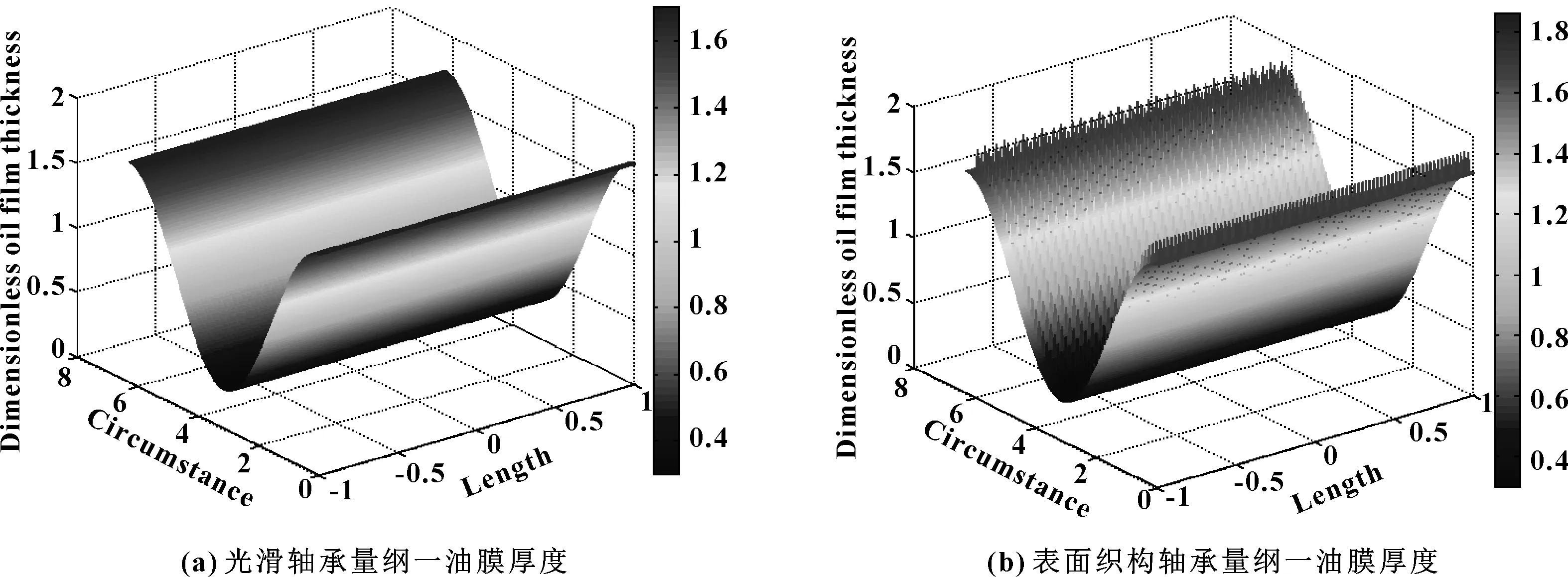
图3 动压滑动轴承量纲一油膜厚度三维分布图

1.3 表面织构轴承Reynolds方程量纲一化

表面织构轴承解析模型的分析中，为了提高分析结果的普遍性，对Reynolds方程量纲一化处理。经过量纲一化处理后，分析中的变量相对减少，方程式结构更加紧凑，突出强调相关变量的影响，且减小无关变量对分析结果的干扰。量纲一化后的结论，提高了结论的适用性。

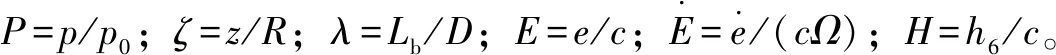
其中Reynolds方程(1)表示了一个非齐次二阶偏微分方程，其中油膜压力P(x,θ)是一个随着轴向和圆周两个方向变化的函数。对织构油膜厚度进行轴向和圆周方向求导得：

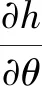
(14)

(15)

联立式(14)、(15)和式(1)，对表面织构轴承Reynolds方程式(1)进行量纲一化后得：

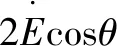
(16)

式中：P表示织构轴承量纲一油膜压力；p0在织构轴承中表示为p0=6μΩR2/c2

式(16)中，等式的左边是一个二阶偏导数，右边是油膜压力在圆周方向随着角度变化而变化的函数表达式。令等式右边油膜压力圆周方向的函数表达式为f(θ)，则有：

(17)

1.4 表面织构动压轴承油膜压力解析表达式

表面织构轴承油膜压力P(ζ,θ)是由沿轴向分布压力u(ζ)和圆周方向分布压力v(θ)两部分组成。分离变量后变成轴向压力u(ζ)和周向压力v(θ)两部分。为了求解织构轴承油膜压力的分布，采用分离变量的方法对表面织构轴承油膜压力分布P(ζ,θ)进行变量分离，则，表面织构轴承油膜压力P(ζ,θ)分离变量后为

P(ξ,θ)=u(ξ)v(θ)

(18)

式(18)经过分离变量后，织构轴承在圆周方向的函数v(θ)为

(19)

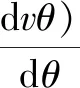
(20)

经过求解后，式(20)中Z(θ)的解集如下：

(21)

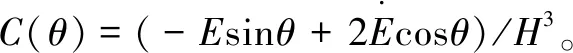
为得到圆周方向油膜压力v(θ)的函数表达式，对式(21)两端进行积分，则有：

(22)

织构轴承油膜压力P(x,θ)在圆周方向压力v(θ)函数中的c1、c2和C表示常数。令C=0，经过整理后得到周向油膜压力v(θ)函数表达式如下：

(23)

表面织构轴承油膜在Sommerfeld油膜边界下周向油膜压力分布为

(24)

Sommerfeld油膜边界下周向油膜压力v(θ)函数中的常数c1和c2表示如下：

(25)

(26)

在Sommerfeld油膜边界下，圆周方向油膜压力v(θ)分布如图4所示。

表面织构轴承油膜压力P(ζ,θ)沿轴向油膜压力为u(ζ)。为求解织构轴承轴向油膜压力u(ζ)，对式(17)等式左右两端同乘sin(θ-θ1)/H3，织构轴承周向由θ1向θ2变化。令，

a2=d1/d2;b=d3/d2;

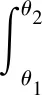
(27)

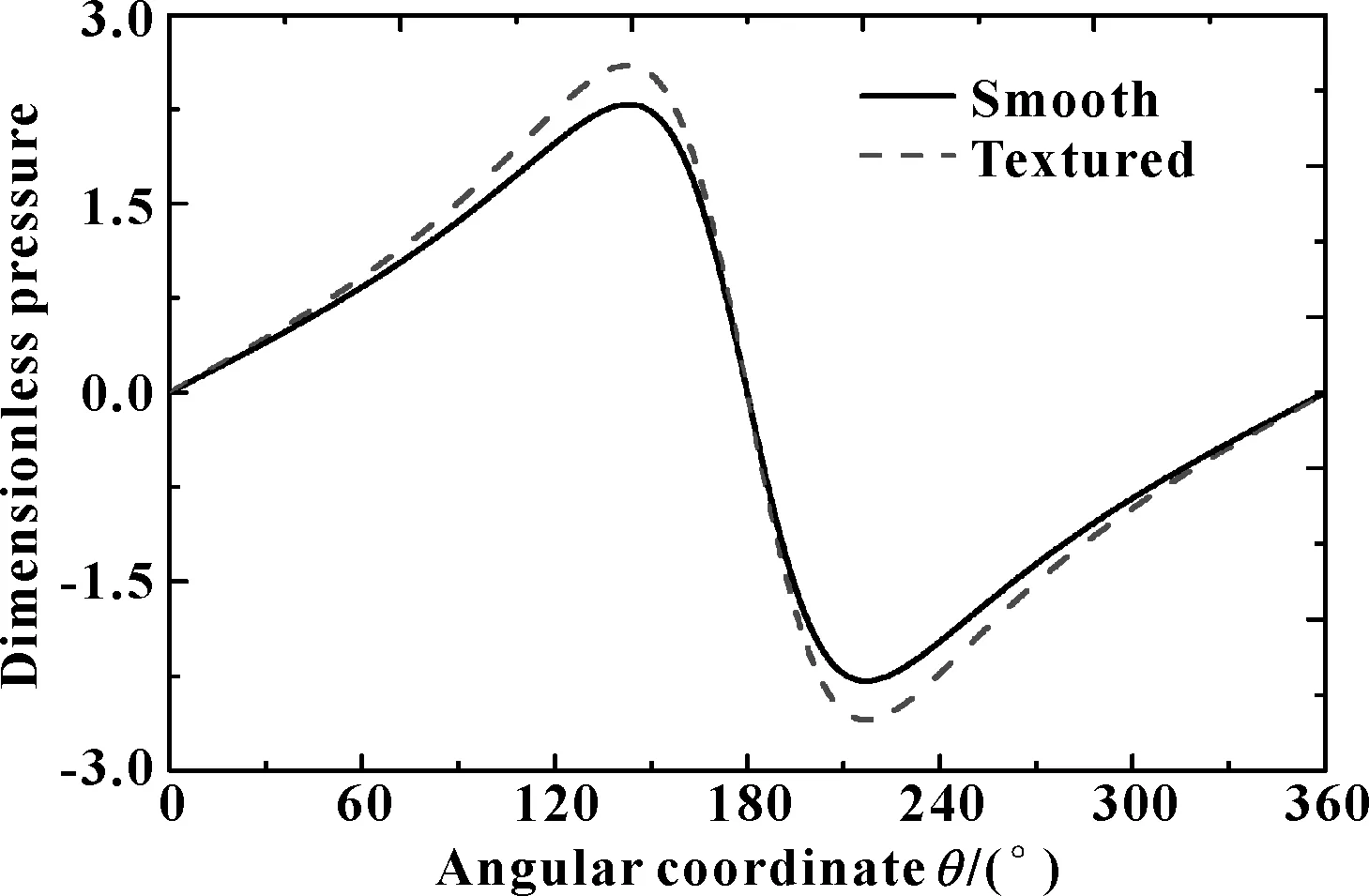
图4 周向量纲一油膜压力分布

轴向的Sommerfeld油膜边界条件：

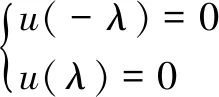
(28)

式(27)为二阶常系数非齐次微分方程，而该方程等式的右边常数b存在3种情况：

(1)假若b=0时，式(27)变成一个二阶常系数齐次方程，该方程的解表示如下：

u(ζ)=c3ζ+c4ζ

(29)

此种情况(b=0)不可能存在。因此，二阶常系数齐次方程求解得出的解应该舍去。

(2)假若b>0时，式(27)变为一个二阶常系数非齐次方程，且该方程的特征方程存在2个不同的特征值。那么，该方程的解表示如下：

u(ζ)=c5cos(bζ)+c6sin(bζ)

(30)

满足式(30)条件的是一对共轭复根特征值，而等式(27)虽然存在2个不同的特征值，但不存在一对共轭复根特征值。因此，没有可被接受的虚数解。故，二阶常系数非齐次方程(27)的解不符合该方程的需要，应舍去。

(3)假如b<0时，式(27)变成一个二阶常系数非齐次方程，且该微分方程的特征方程存在2个不相等的实根特征值。该方程的解表示如下：

u(ζ)=c7eaζ+c8e-aζ

(31)

式中：ci(i=3，4，......，8)表示常数。表面织构动压轴承在Sommerfeld油膜边界下确定常数ci后，将常数ci代入式(31)，即可得到二阶常系数非齐次微分方程的解：

(32)

表面织构轴承在不同ζ下的轴向油膜压力u(ζ)分布，如图5所示。

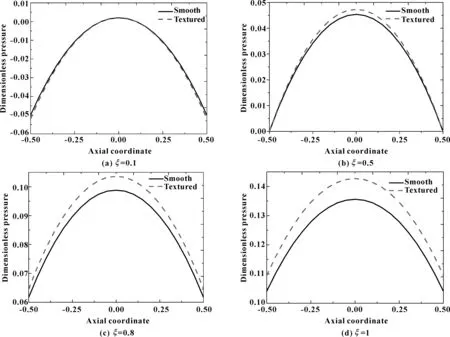
图5 轴向油膜压力u(ζ)分布

在图5中，油膜压力在轴向表现为一种抛物线形状，且光滑轴承和织构轴承油膜压力随着ζ的变化，轴向油膜压力值分布也不相同。光滑轴承轴向油膜压力值在ζ=0.1下普遍高于织构轴承轴向油膜压力值；而织构轴承轴向油膜压力值在ζ≥0.5下大于光滑轴承轴向油膜压力值，即，随着织构轴承ζ增加，轴向压力值呈现一种逐渐大于光滑轴承轴向油膜压力值的规律。结果表明，织构轴承轴向油膜压力受到ζ的影响，有且只有当织构轴承的ζ≥0.5时，轴承内表面的织构才能起到更好的承载作用。

联立式(23)、(32)、(18)，经整理可得到织构轴承油膜压力P(ζ,θ)解析式为

(33)

2 圆形凹坑轴承油膜力解析式

式(33)表述了圆形凹坑织构轴承的油膜压力分布。织构轴承在径向Fx和切线方向Fy的油膜力表示如下：

(34)

由织构轴承油膜力F的定义，从而得到表面织构轴承油膜力Fx和Fy分别表示如下：

(35)

(36)

因此，表面织构轴承油膜力F为

(37)

3 算例与分析

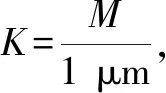
3.1 凹坑结构参数对油膜压力的影响

动压滑动轴承在旋转过程中，轴径渐由发散区域(降压区)进入到收敛区域(升压区)。为了分析凹坑结构对织构轴承油膜压力的影响，选择圆形微凹坑深度T=6，凹坑间距K分别为0.2、0.5和1，表面微凹坑对织构动压滑动轴承油膜压力的影响如图6所示。

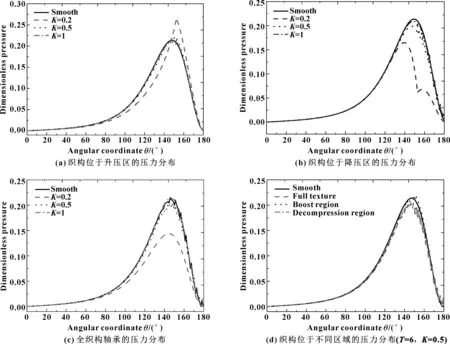
图6 不同间距的凹坑轴承油膜压力分布

从图6(a)可看出：织构轴承油膜压力值高于光滑轴承油膜压力值。因为微凹坑存在收敛区域时，织构轴承油膜压力由于受到收敛间隙与表面微凹坑二者共同作用，使得旋转的动压滑动轴承产生的动压作用叠加。因此在该区域内的织构对于轴承的作用是积极的，即有利于润滑和承载。当轴径旋转至降压区时，如图6(b)所示，光滑轴承的油膜压力高于织构轴承。凹坑轴承间距K=0.2时的量纲一油膜压力约为光滑轴承的77.2%。此时，织构轴承受到的影响最为显著，且油膜压力在变化过程中存在2个峰值，使得油膜压力明显下降，从而引起润滑和承载能力下降。从图6(c)可看出：对于全织构轴承，当织构间距K在0.2～1之间变化时，轴承的量纲一油膜压力分布趋近于光滑轴承。因此，全织构轴承不仅不会提高轴承油膜压力，且织构密度还影响着油膜压力，即织构越密集，油膜压力下降越显著。

选择圆形凹坑轴承的织构参数T=6，K=0.5，得到的不同位置区域的织构轴承油膜压力如图6(d)所示。可知：织构位于升压区时，圆形凹坑织构轴承的油膜压力总体变化趋势略高于光滑轴承；而光滑轴承的油膜压力却明显高于织构位于降压区的轴承和全织构轴承，说明全织构与位于降压区的织构不仅不能提高油膜压力，还在一定程度上降低了油膜压力；织构位于降压区的轴承与全织构轴承的油膜压力变化趋势虽基本一致却有略微不同，表明全织构相较降压区的织构在承载和润滑方面具有一定的优势。故，织构位于升压区的轴承在润滑和承载性能方面优于其余3种条件下的轴承。综上所述，为提高轴承的润滑和承载性能应将织构加工在轴承的升压区[10]。

取表面织构轴承间距K=0.2，深度T分别为2、10和30，表面织构对轴承油膜压力的影响如图7所示。

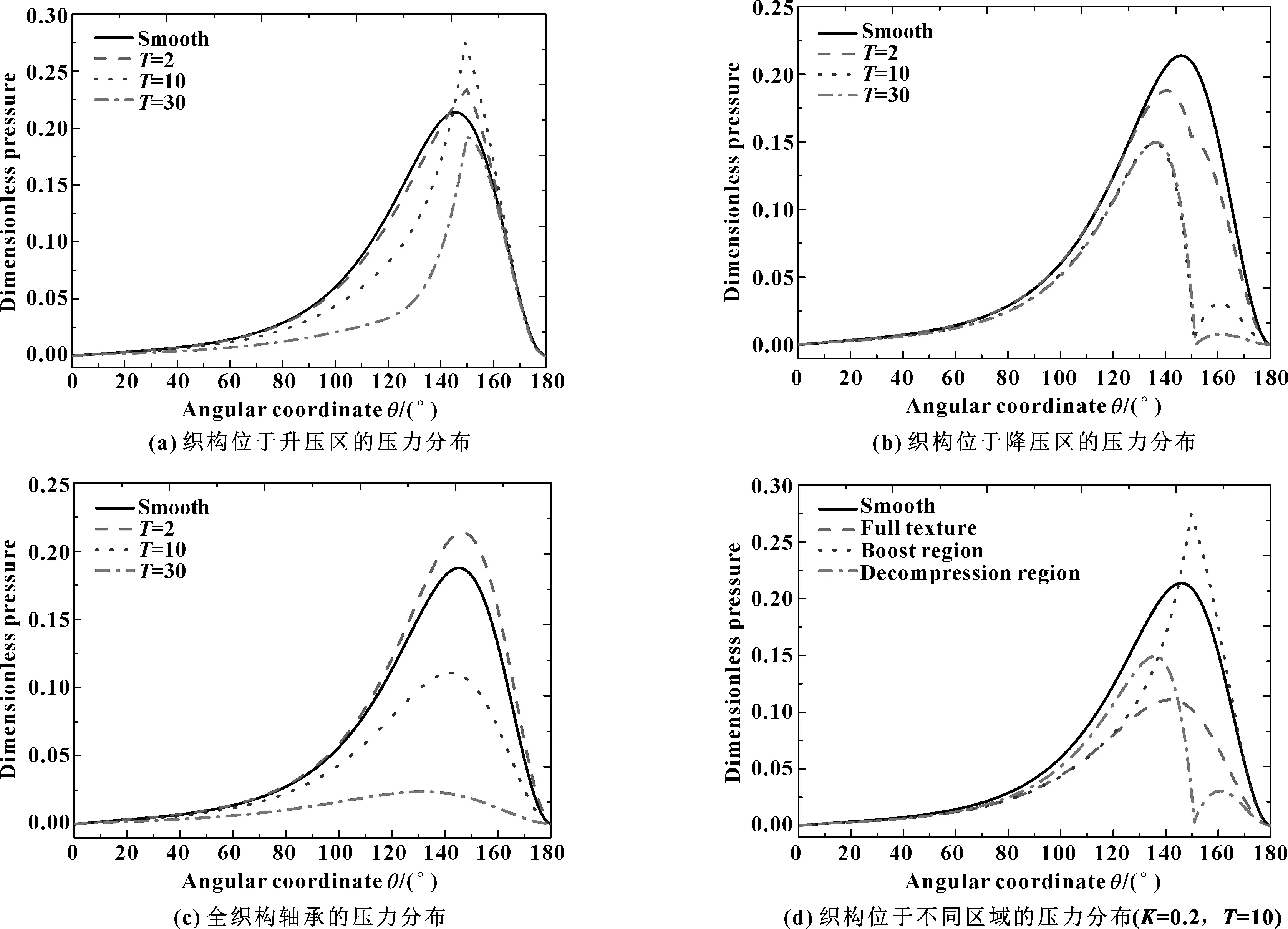
图7 不同深度的织构轴承油膜压力分布

由图7(a)可看出：织构存在收敛区域时，油膜压力发生不同的变化，这是由于间隙收缩形成的动压效应与增加的油膜二者共同作用的结果。由图7(b)可看出：轴径旋转至降压区时，织构深度T在2～30变化范围内，轴承发生空化现象越发显著，表明存在于降压区的织构对轴承的润滑和承载性能不利。由图7(c)可看出：不同深度的全织构轴承油膜压力变化明显，表明织构深度对轴承的油膜压力产生明显的影响，且深度愈深，压力愈小。

为了比较不同位置区域的织构轴承油膜压力，选择圆形凹坑织构轴承的织构参数K=0.2，T=10进行对比，如图7(d)所示。可知：织构位于升压区时织构轴承的油膜压力峰值明显高于光滑轴承，表明轴承在该织构参数下的动压效应更突出；而光滑轴承与全织构轴承在油膜域内的油膜压力分布均表现得比较平稳，不存在突然变化的动压；相较于全织构而言，织构位于降压区的轴承动压出现了波动性，这会引起振动的增加，不利于润滑和承载，进而造成摩擦磨损的增加。因此，织构位于升压区的轴承动压效应优于其他状态下的轴承，且轴承的润滑与承载性能也最佳。

3.2 不同长径比下织构轴承油压力分布

根据式(33)，不同长径比下圆形凹坑织构轴承油膜压力分布如图8所示。可以看出：不同长径比(L/D)下的圆形凹坑织构轴承最大油膜厚度位于θ=120°～150°处，最小油膜厚度位于θ=0和π处；且该织构轴承在0≤θ≤π区域内量纲一油膜压力分布近似一种连续的抛物线分布；随着长径比(L/D)的增加，最大油膜厚度下的最大量纲一油膜压力也不断增加。而由图5可知，在织构轴承轴向上，量纲一油膜压力分布表现为抛物线分布，原因在于织构轴承两端产生了泄漏，故此油膜压力是0。比较图8中不同长径比(L/D)下的油膜压力曲线可知，文中提出的方法的计算结果同文献[11-16]的结果基本一致，证明文中提出方法的正确性和有效性。

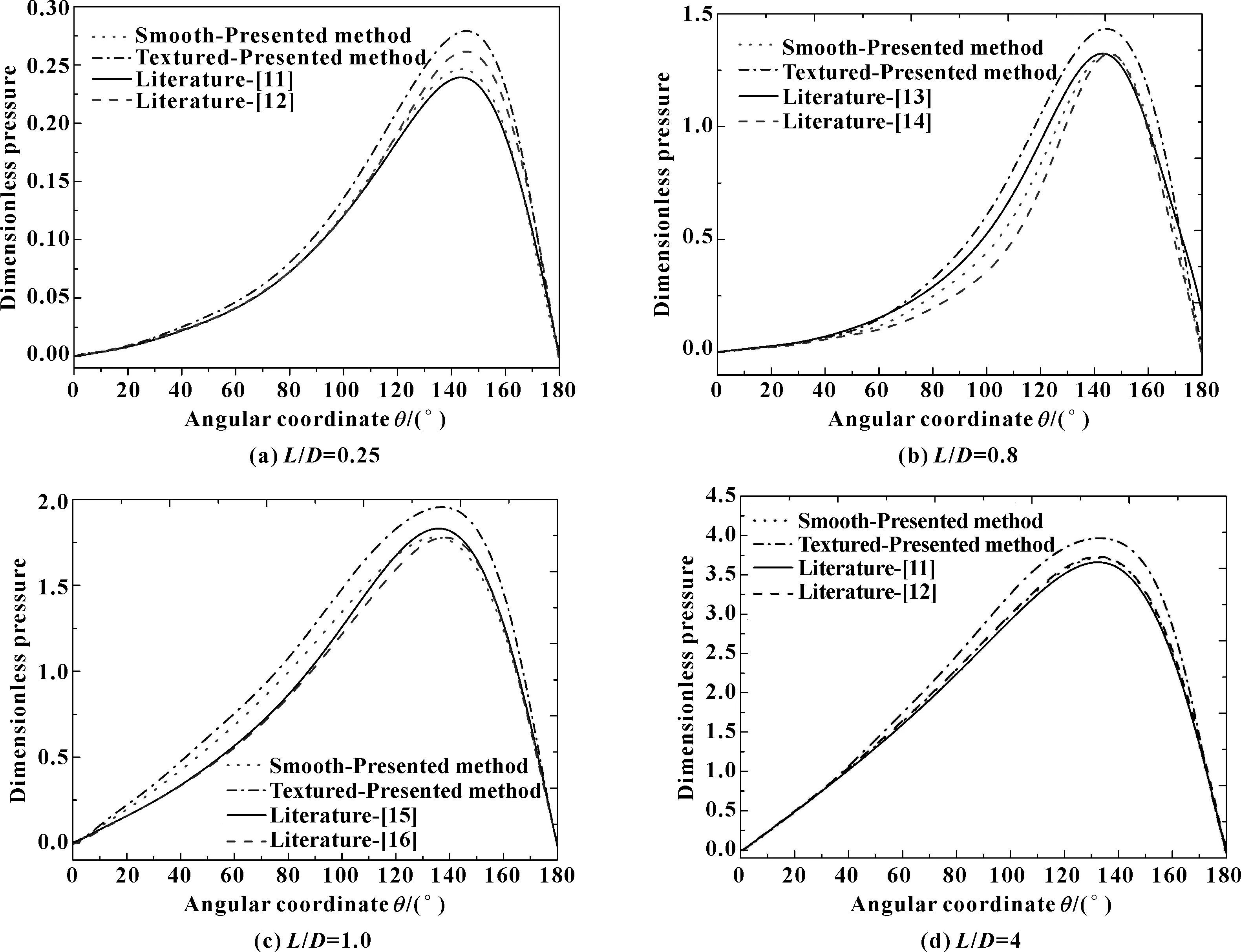
图8 不同长径比(L/D)下量纲一油膜压力分布

3.3 偏心率(ε)对油膜力Fx和Fy的影响

根据式(35)、(36)可得到圆形凹坑织构轴承油膜Fx和Fy与偏心率(ε)的关系，如图9所示。图9中，织构轴承非线性油膜力Fx和Fy随偏心率(ε)的变化趋势相似，均是随偏心率的增加而非线性增加；且在相同偏心率下织构轴承径向油膜力Fy高于轴向油膜力Fx。

比较图9中不同偏心率下的油膜压力Fx和Fy曲线可知，文中提出方法的计算结果同文献[17]的结果基本一致，证明文中提出方法的正确性和有效性。

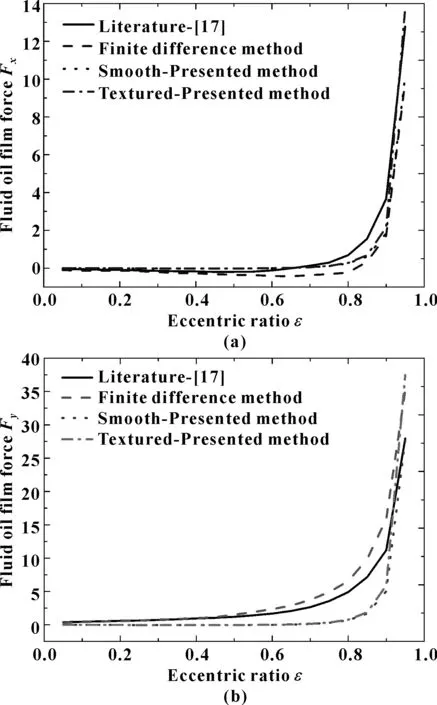
图9 油膜力Fx和Fy与偏心率(ε)的关系

4 结论

(1)基于Sommerfeld油膜边界，通过分离变量的方法对表面织构轴承Reynolds方程进行解析，并对织构轴承的油膜力解析式进行推导。

(2)利用油膜压力解析式，对凹坑结构表面织构轴承在升压区、降压区和全织构下的油膜力进行分析，结果表明，升压区的表面织构承载和润滑性能提升显著；而降压区和全织构时的表面织构承载和润滑性能不佳。

(3) 凹坑结构表面织构轴承在不同长径比下的油膜压力分布近似呈连续的抛物线分布；而油膜力Fx和Fy变化趋势相似，均是随偏心率的增加而非线性增加。对比文献中不同长径比和偏心率下油膜力，验证了作者提出方法的正确性和有效性。