弹簧振子链系统的振动局域化现象研究

赵 鹏， 纪 刚， 周其斗， 谭 路， 唐永壮

(海军工程大学 舰船与海洋学院，武汉 430033)

周期系统在航空航天、土木建筑、机械工程等领域广泛存在。理想周期系统(无阻尼)在频域上表现为“通频带”和“止频带”特性。当激振频率处于通频带时，波动会无损失地传遍整个系统。当激振频率处于止频带时，波动的幅值和能量会表现出衰减特征。

然而在实际生产中，由于材料不均匀性或制造误差，实际结构会与设计目标存在偏差[1]，小偏差将对系统的振动传递特性有较大的影响。因为振动频率即使处于理想周期系统的通频带内，结构的不规则性也会导致波的能量局限在小范围内，从而形成局部振荡[2]。所以分析非周期系统波动的衰减机理可以为振动控制提供理论依据。

国外对振动局域化现象的研究较早，Hodges[3]最早开始在结构领域中研究非周期结构的局域化效应。由于实际模型都可类比为弹簧振子链，因此Hodges和Woodhouse最早开启了弹簧振子链的局域化研究，并通过试验证明了非周期耦合弹簧振子系统存在局域化现象。在含有阻尼的局域化效应研究方面，Langley[4]分析了含有阻尼一维结构的振动模态局域化，研究了阻尼对响应的影响，发现阻尼与系统一定不规则程度引起的局域化系数具有相同的量级。Castanier等[5]研究了空间简支梁中阻尼和非周期性对结构动力学特性的综合影响。以上研究内容主要基于统计理论的数学手段开展证明，并通过蒙特卡罗数值方法模拟统计特性，因此未曾在实例模型中得到验证。本文将从能量传递角度，分析具体实例模型振动幅值和能量的变化情况，定量化计算衰减因子并与模型验证，同时深入分析无序和阻尼引起结构振动衰减特性的一般规律。

本文将以含有对地刚度的弹簧振子链系统为研究对象，基于波传递理论，分析当子单元对地刚度无序分布时的局域化系数，以及周期结构存在阻尼时的振动衰减因子，分别给出具体的数学解析表达式。建立相关有限元模型，获得各振子单元的频响分析结果，通过比较理论衰减系数和振动幅值沿轴向的变化情况验证相关结论的正确性。同时分析二者联合作用下的振动衰减效应，对比含有阻尼系数下周期和非周期系统质量单元的频率响应曲线，深入分析阻尼和结构无序对振动传递性能的影响。研究内容可以为工程设计中的振动控制提供技术支撑。

1 无阻尼弹簧振子链系统波动传递分析及衰减因子计算

1.1 具有等对地刚度的周期弹簧振子链系统

周期弹簧振子链系统的平面布置图，如图1所示。将系统的两端进行固支，外界激振力以幅值F，频率ω作用在左端第一个弹簧处，每个振子质量相同均为m，相互之间通过刚度系数为k的弹簧耦合，同时各自又经由刚度为kd的弹簧与大地固接。

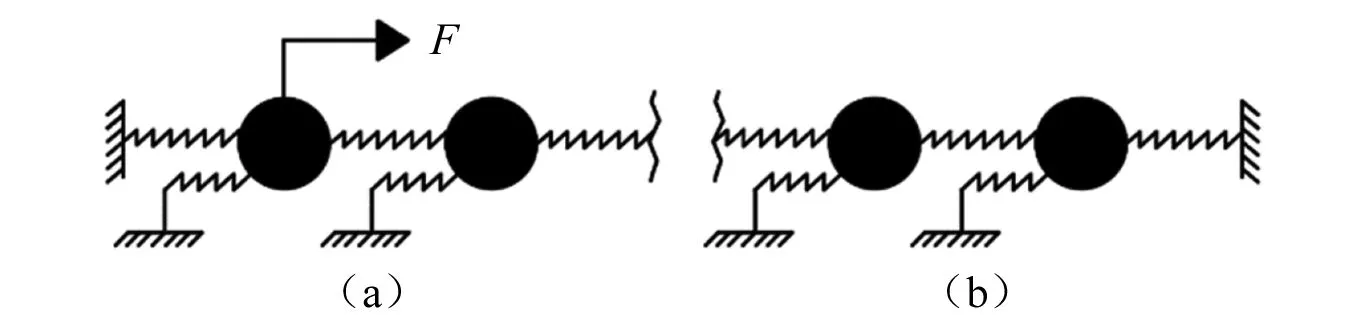
图1 含有对地刚度的弹簧振子链系统Fig.1 Mass-spring system with ground stiffness

设第i个质量单元的位移向量表示为xi，则系统的运动方程可以表示为

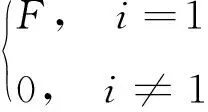
(1)

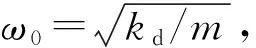
(2)

对于周期系统而言，状态传递矩阵[T]处处相同，由文献[6]知波动衰减系数为

γ衰=ln|λ|

(3)

式中，|λ|≥1，是传递矩阵[T]的特征值，从而解得波动衰减系数表达式

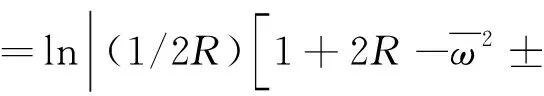
(4)

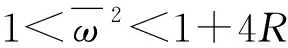
1.2 具有对地刚度无序分布的弹簧振子链系统

改变弹簧振子系统的周期性主要从两个方面着手：①改变振子质量的同一性；②将振子的对地刚度进行无序设计。对地刚度的不一致性在工程中有更广泛的应用，这里将对地刚度进行无序扰动。设第i个质量单元的对地刚度为ki，引入无因次刚度变量Δfi=(ki-kd)/kd，此时单元间的传递矩阵不再处处相同，每一项均是随机传递矩阵

(5)

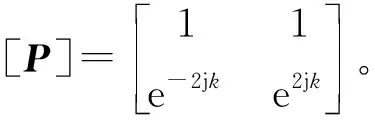
(6)

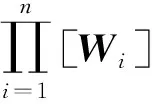
(7)

传递矩阵变化为

Wi=[P]-1[T0+ΔTi][P]=
W0+[P]-1[ΔTi][P]

(8)

连续乘积为

(9)

运用式(6)得到弹簧振子链对地刚度无序分布下的局域化系数理论公式

(10)

式中，σ2为振子无因次刚度系数的统计方差值，在物理含义上表征为结构的无序程度，无序程度越大，局域化系数越大。定量计算公式的推导过程就是对无穷多个随机传递矩阵的乘积取近似，子单元数量越多，理论公式反应的衰减效应越精准。

2 有阻尼弹簧振子链系统的衰减因子计算

第1章是假定弹簧在没有阻尼条件下的波传递行为，单纯考虑无序引起的局域化特征，然而实际结构是有阻尼的，下面分析阻尼对周期弹簧振子链系统衰减效应的影响。

将质量块与大地之间的耦合弹簧均赋予阻尼系数δ，阻尼的存在，使得材料刚度在数学上表达为复数形式，即弹簧具有复数弹性模量，波传递矩阵多了一虚部项

(11)

同理，应用式(3)，得到阻尼引起的衰减因子为

(12)

简化为

(13)

从公式可知，γ阻尼与阻尼系数成正比。在材料属性确定的条件下，由阻尼引起的局域化效应与激振频率密切相关。阻尼衰减因子随无因次频率的变化关系图，如图2所示。通频带中央频率对应的理论值最小，向与止频带的交界处数值逐渐增大。

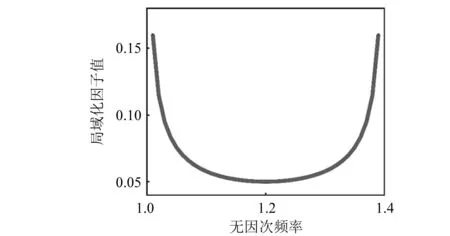
图2 局域化系数随无因次频率的变化关系Fig.2 Variation of localization factor with frequency

3 利用实例模型的数值仿真验证衰减效应

3.1 周期系统通频带的数值验证

对于周期弹簧振子链系统，可以看作是一个弹簧振子单元沿水平方向的周期性复制。由于每个单元间的波传递矩阵完全相同，波在系统中传播不会存在散射，仅存在边界处的反射。对于周期系统，在特定频率下，当传导波和反射波满足一定相位相协条件时，就会叠加形成模态，而这些模态往往会表现出聚集现象[9]。

为验证上述结论，现对含有对地刚度的弹簧振子链系统进行有限元分析。弹簧振子链模型的相关参数和材料属性，如表1所示。

表1 周期弹簧振子链模型相关参数Tab.1 Related parameters of periodic spring oscillator chains

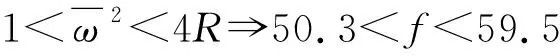
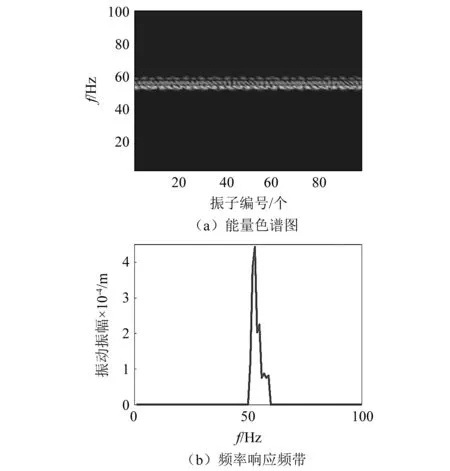
图3 周期系统的通频带Fig.3 The passband of periodic system

3.2 对地刚度无序引起的衰减效应验证

周期系统中弹簧振子的对地刚度为1×105n/m，现设计扰动刚度的最大偏移量为1×104n/m，即对地刚度在区间(90 000,110 000)服从均匀分布，通过随机函数程序给出99个振子的对地刚度系数，算出一组数据的无因次方差。将99个数值赋予给模型的对地刚度系数属性，重新进行有限元分析，得到的“能量-频率-位置”关系的色谱图，如图4所示。对比周期系统的色谱图可以发现，“亮带”发生了明显变化，即使在通频带也发生了能量局域化现象。

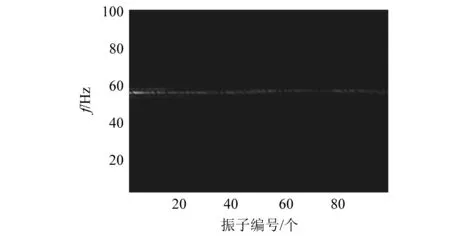
图4 非周期系统能量色谱图Fig.4 The contour map of aperiodic system

当f=53 Hz,f=57 Hz时的系统振动幅值图，如图5所示。在第30～第40个振子间振幅基本衰减为0，由于对地刚度的无序特征，振动主要被控制在激振源附近。

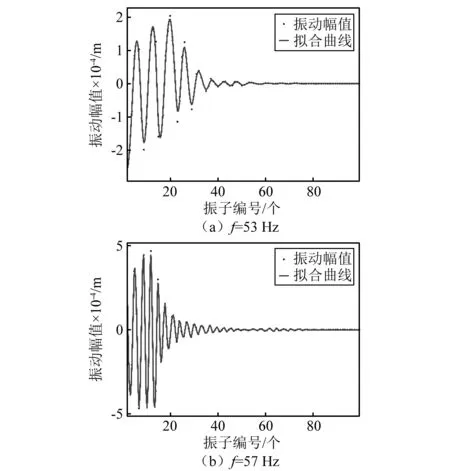
图5 典型频率下的振动幅值图Fig.5 Vibration amplitudes of typical frequency

对振动幅值取对数后，与理论预报结果进行对比，如图6所示。

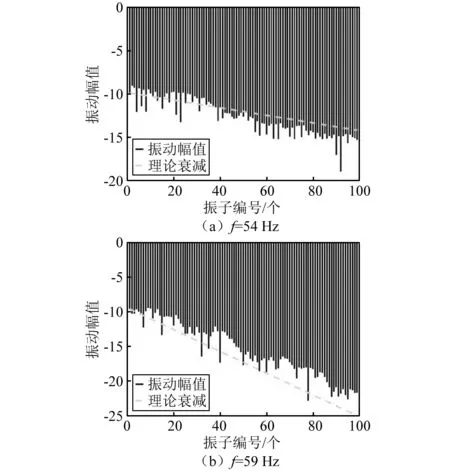
图6 振动幅值曲线同理论局域化系数的比较Fig.6 Comparisons of vibration amplitudes and theoretical results

即使在外界激振力不变的情况下，弹簧振子系统受迫振动的频率响应也随着系统无序程度的大小和分布而变化。当振子数量足够多时，振幅会沿着振子链呈现指数衰减的趋势。理论推导的预报结果反映了单元幅值在空间上衰减的整体平均效应。

从图6可知，由对地刚度无序引起的局域化系数理论公式与有限元结果相当吻合，理论公式可有效地反映振动衰减特征。

3.3 阻尼引起的衰减效应验证

在周期弹簧振子链模型的基础上赋予阻尼系数0.01，代入式(13)计算通频带内各激振频率对应的衰减因子，与有限元模型分析得到的幅值拟合情况如图7所示。

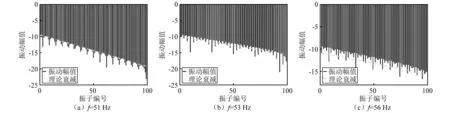
图7 振动幅值变化同理论局域化系数的比较Fig.7 Comparisons of vibration amplitudes and theoretical results

阻尼使得周期系统不再存在通频带，振幅在整个频域上的响应都呈现出均匀的衰减趋势。从理论预报与有限元模型分析的对比情况来看，阻尼引起的局域化理论公式非常精准地反映出了波幅的变化规律。

4 阻尼和无序引起的振动衰减特性对比研究

对于周期有阻尼系统，每个振子之间的波传递矩阵都是相同的，局域化系数的表达式是精确的。而对于非周期无阻尼系统，每个振子之间的波传递矩阵是随机扰动的，所以在公式推导中采用了Furstenberg定理的传递矩阵理论，当随机矩阵的数量趋于无穷大时，其连续乘积的极限值为一个常数[10]，从而使得非周期系统的局域化系数有解析值存在。所以由无序引起的局域化系数理论公式适用于子单元数量无限多的情况，其反应了一个总体平均的效果。

由系统结构无序引起的局域化特征和阻尼引起的振幅衰减趋势相似，可见结构的无序性好像给系统赋予了阻尼，但又区别于阻尼，这是从结构的角度改变了系统的振动特征。

现分析在阻尼和结构无序联合作用下的振动传递衰减现象，此时系统的波传递矩阵同时包含了阻尼项和无序项，总的衰减因子由两者共同贡献

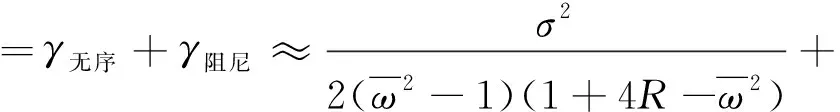
(14)

在3.2节非周期弹簧振子链模型的基础上赋予不同的阻尼系数0.000 1，0.001，0.01和0.1，观察在通频带中央频率f=55 Hz处，无序和阻尼联合作用下的局域化效果与理论预报公式的对比情况，如图8所示。

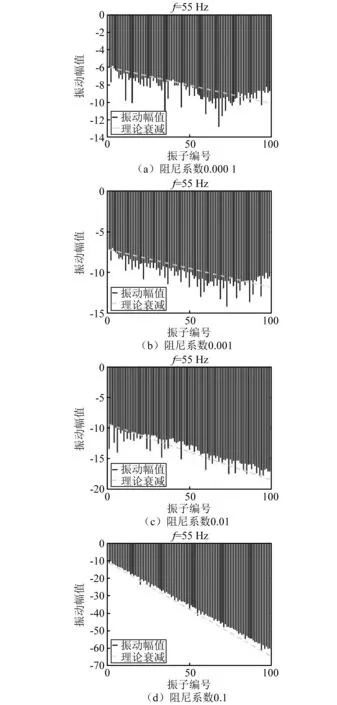
图8 振动幅值变化同理论局域化系数的比较Fig.8 Comparisons of vibration amplitudes and theoretical results

通过观察理论衰减线的斜率和振动幅值的变化趋势可以看出，当阻尼系数为0.000 1和0.001时，阻尼对振动传递的影响很小，系统的振动衰减特征主要由结构无序贡献，振幅大致遵循指数衰减的趋势。随着阻尼系数增大为0.01时，阻尼和无序对局域化的贡献近乎相等，振幅变化比较平稳，但有个别响应分布在理论预报结果的两侧。当阻尼系数为0.1时，振幅变化非常平稳，严格按照指数规律衰减，此时系统的局域化效应主要由阻尼决定(见图8(d))。

这说明由结构无序引起的空间衰减是指数渐近的，理论预报公式反映了大量数据下的平均效果，所以个体的实现可能与理论结果有一定的偏差。另一方面，阻尼在每个子单元处都是相同的，振动会沿着各单元产生均匀的衰减，阻尼局域化预报公式是精准的。

在分析了单频激振下所有质量单元的响应后，现在单独分析某一子单元在一系列激振频率下的振动行为。选择对地刚度最大扰动量10%，阻尼系数0.01，由99个弹簧振子组成的系统。第1个和第25个质量单元的频率响应，如图9所示。

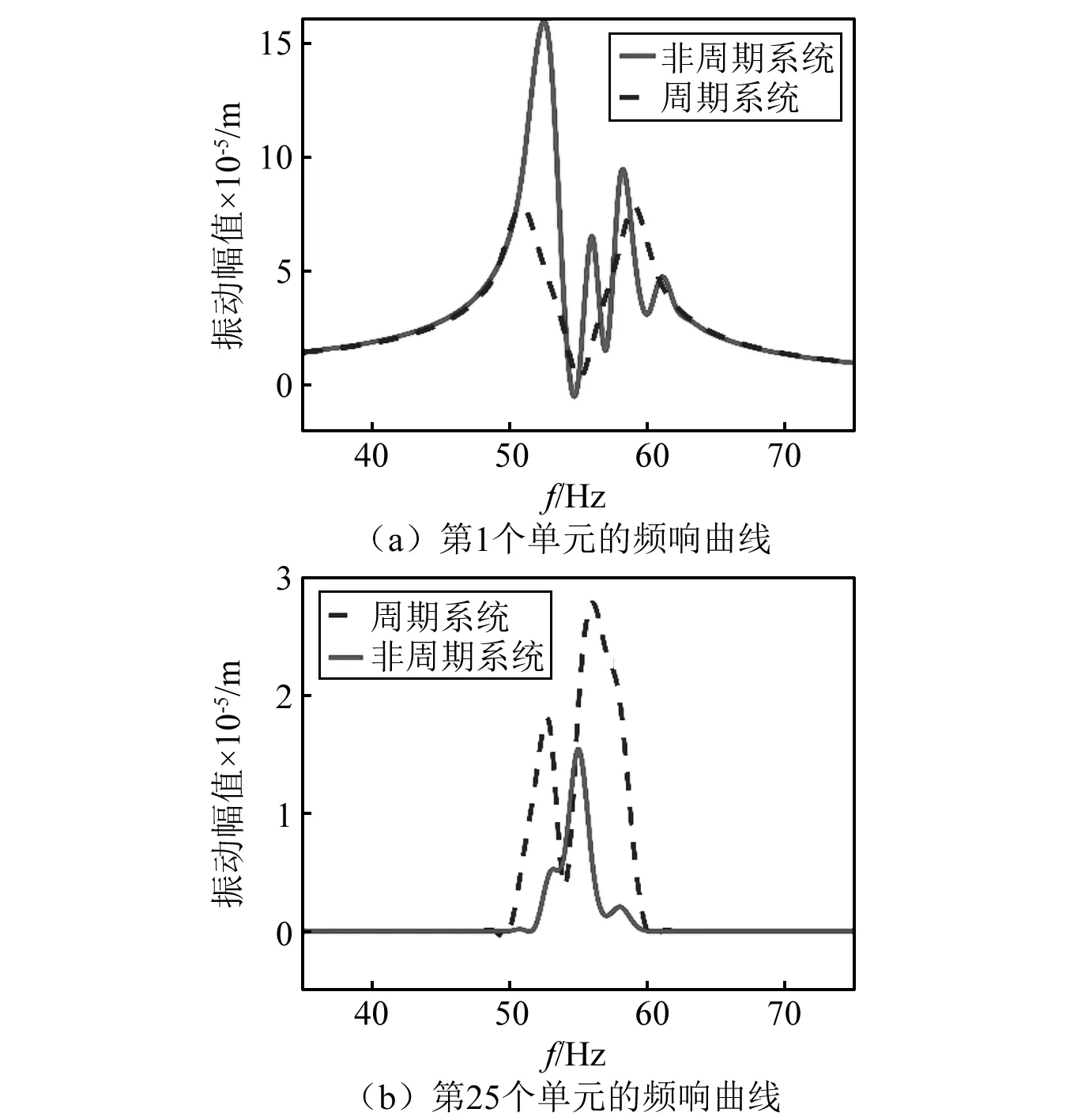
图9 振动幅值随频率的变化曲线Fig.9 Variation curves of vibration amplitudes with frequency

观察第1个振子的频率响应曲线可知，结构在通频带(51～59 Hz)处的响应幅值更大，并且通带内存在几个峰值。因为在这些频率下，局部模态在第1个质量单元附近被激发。图9中虚线为相同阻尼系数下的周期系统，波峰数量明显少于非周期系统。在大部分频率范围内，非周期结构表现出了更大的响应，这说明非周期系统在靠近激振源附近处的能量更大，根据能量守恒原理，远离振源处的能量会很小，即振动被“局域化”。结构无序导致了单元幅值在空间上的衰减，因为传递过程中能量在每个单元处都存在散射。远离中通带时，能量的散射更为普遍，这也从理论公式中得到证明，因为通频带边缘处无序局域化系数达到最大值。

非周期结构下第25个振子的频响曲线明显不同于第1个振子，其在形状上更趋向于周期结构，传递到第25个振子处的能量已经衰减很多，但响应比周期结构更小。可以观察到无序引起空间振幅衰减的基本性质，结构无序会使能量在单元处发生随机散射，相比于周期结构，响应在激振源附近更大，在远离激振源的位置更小。

5 结 论

本文以弹簧振子链为研究对象，研究了对地刚度无序分布和阻尼对结构振动传递特性的影响。分别推导出了二者引起的振动衰减系数，并通过有限元分析实例模型验证了相关结论，深入分析了无序和阻尼对系统振动传递特性影响的一般规律。

(1)γ阻尼的表达式非常精准地反映了振动幅值的变化情况，因为系统的传递矩阵是确定的。而γ无序推导过程中运用了统计扰动理论，得到的是近似解，反映了大量数据下的平均衰减效应。

(2) 结构的无序会产生与阻尼类似的振动衰减效应，但阻尼和无序引起局域化特征的物理机制是不同的。阻尼使得激振能量在系统中均匀耗散，每个单元处的衰减效果相同。然而对于无序结构，由于每个子单元处的阻抗不同，入射波会在每个振子处发生散射，并且散射量不相同，从整体平均效果上看，空间振动幅值会呈现指数衰减的趋势。

(3) 阻尼会使振动能量发生耗散，而结构无序是将振动能量局限在一定区域，并没有使能量减小，利用结构无序的局域化效应可以实现振动传递的控制。此时若在振源附近敷设高阻尼材料，可使结构总的振动能量发生衰减，防止振动被局限化后应力集中影响设备的使用寿命。