正梯度冲击下冻结红砂岩力学性能及损伤效应研究

张慧梅， 陈世官， 王 磊， 袁 超

(1. 西安科技大学 理学院，西安 710054;2. 西安科技大学 建筑与土木工程学院，西安 710054)

随着我国煤炭资源开发向西部矿区转移，西部矿区将迎来新的一轮建井热潮，而西部煤炭资源多为侏罗系煤层，其上覆巨厚白垩系富水基岩，具有胶结力弱、强度低等特征，故在煤矿立井的建设中多采用冻结法施工，以达到止水、提高软弱围岩强度的效果[1]。但在实际建设过程中，由于冻结方案的选取不合理等原因，使得冻结交圈不彻底的冻结壁在遭受工程爆破荷载时发生破坏，出现渗水及透水事故[2-3]。因此，研究冲击荷载下冻结软岩的动力响应规律，为工程安全施工提供基础理论依据。

到目前为止，许多学者从不同的角度对软岩进行了大量的研究。Shen等[4-5]研究了不同热处理后砂岩的损伤特征。Bai等[6-7]研究了冻结砂岩在三轴压缩应力下的变形机制和强度特征。刘波等[8-9]在不同冻结温度和围压下对不同含水率红砂岩进行了三轴试验，并指出地应力的作用增强了红砂岩的孔隙限制能力和抗冻胀性。Wang等[10]研究了冻结砂岩在不同荷载下的微观破坏机制，发现砂岩中的冰在压缩下具有支撑和填充作用，而未冻结的水膜在拉伸和剪切下起胶结作用。Liu等[11-12]基于核磁共振(nuclear magnetic resonance， NMR)研究了寒冷地区岩石的孔隙演化特征。

国内外学者对冲击作用下冻结软岩及各类岩石的力学性质也进行了大量研究。Wang等[13-14]研究了冻结砂岩在冲击载荷作用下的力学性能和能量耗散规律，发现不同温度下红砂岩的动态力学性能差异是由冻结岩石介质不同的水冰相变和冷收缩率造成。马冬冬等[15-16]在不同围压和温度条件下对人工冻土进行了霍普金森压杆(split Hopkinson pressure bar，SHPB)试验和动态本构模型研究。Shan等[17]利用SHPB装置研究了冻结红砂岩的动力学。当平均应变率较低时，损伤仅分布在试样边缘。然而，随着平均应变率的增加，损伤范围向试样中心扩展。Hu等[18]研究了花岗岩在低速循环冲击下的机械响应和能量耗散特性。Li等[19]研究了单轴冲击压缩载荷和低温耦合作用下含水大理岩的本构模型。张蓉蓉等[20]对冻融和热冲击循环作用下红砂岩的动态力学性能和本构模型开展了SHPB试验研究。Yang等[21-23]对冻结饱和红砂岩进行了SHPB试验，以研究冻结砂岩在冲击下的破坏机理和强度变化特征。纪杰杰等[24]研究了冲击荷载作用下岩石破碎分形特征及动力学特性。杜超超等[25-26]研究了动静组合加载和被动围压下复合岩样及煤岩的动态力学特性。

虽然国内外学者对冻结软岩及各类岩石的静、动力学进行了大量的研究，取得了许多优秀的成果，然而，考虑实际工程的研究较少。因为，在冻结软岩凿井施工中，冻结壁受到的冲击荷载并不是均匀的、一成不变的，而是有强弱顺序和方向性的，当爆破区域距离冻结壁较远时，冻结壁内损伤体将受到拉剪破坏，随着凿井掘进的不断深入，损伤体受到的冲击应力波不断加强，表现为典型的正梯度冲击(即冲击载荷逐步增加)，如图1所示，损伤体的破坏由拉剪破坏向压剪破坏转变。

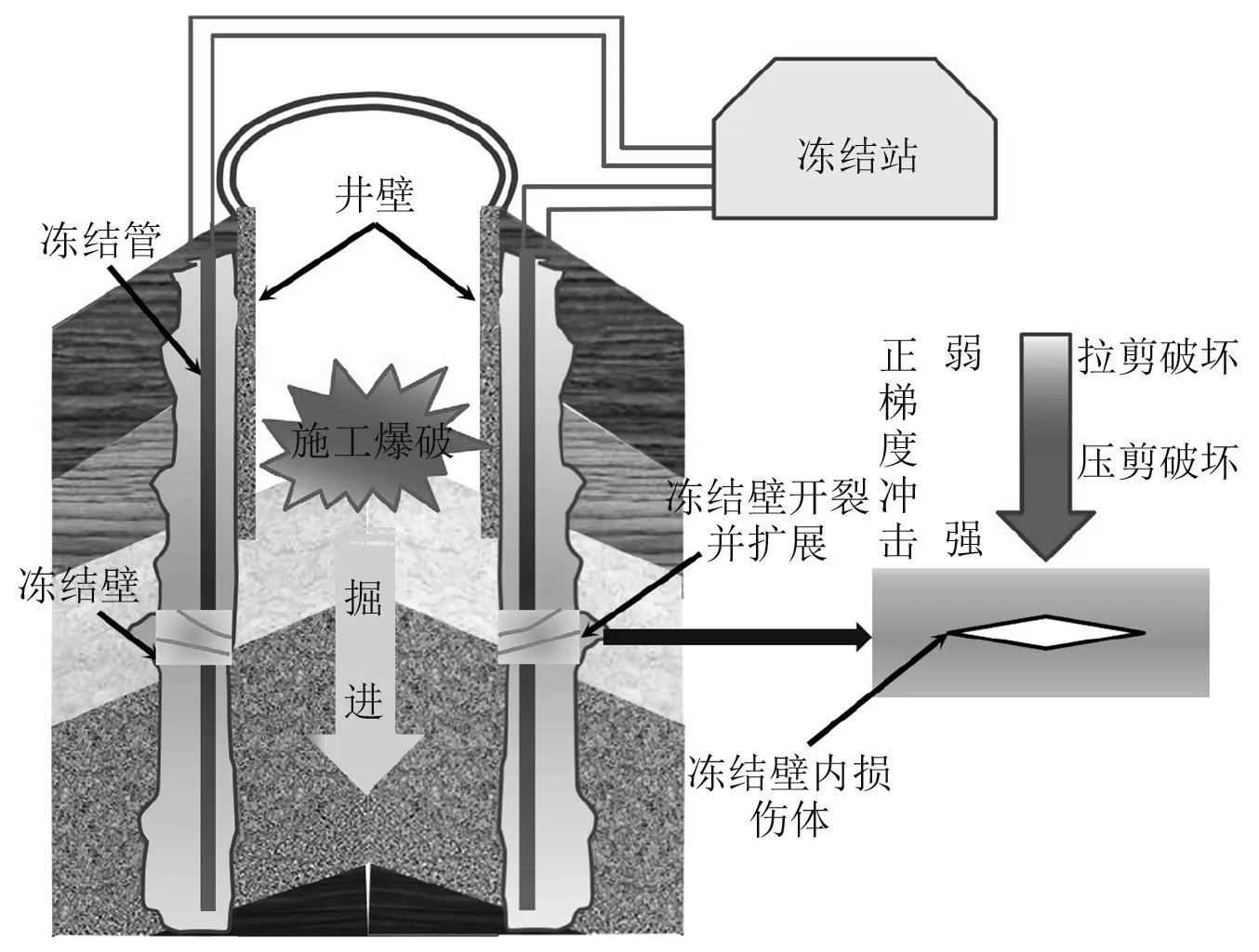
图1 冻结壁受荷示意图Fig.1 Schematic diagram of frozen wall under load

因此，本文利用SHPB装置在不同冻结温度(25 ℃，-5 ℃，-10 ℃，-15 ℃和-20 ℃)下对红砂岩进行了正梯度冲击压缩试验，并利用NMR系统测量了冲击后岩石样品的孔隙变化参数，以研究损伤演化规律。研究结果可为寒冷地区岩质边坡、隧道和矿井的施工提供有益的指导。

1 试验材料和方法

1.1 试样制备

试样取自西部矿区的白垩系洛河组红砂岩，是典型的弱胶结砂岩(后文中统称为红砂岩)，颜色暗红、质松，由泥质胶结物组成，利用X射线衍射仪对其进行矿物成分及表面能谱分析，如表1和图2所示。发现起主要胶结作用的黏土矿物蒙脱石和绿泥石等含量总占比仅有8%，其化学成分以二氧化硅含量最高，分别达到了20.34%和12.19%；其次为氧化铝，含量分别为8.72%和4.5%，以无机胶结形式将颗粒胶结或包裹在一起，具有一定的黏结强度。

表1 矿物成分表Tab.1 Mineral composition table

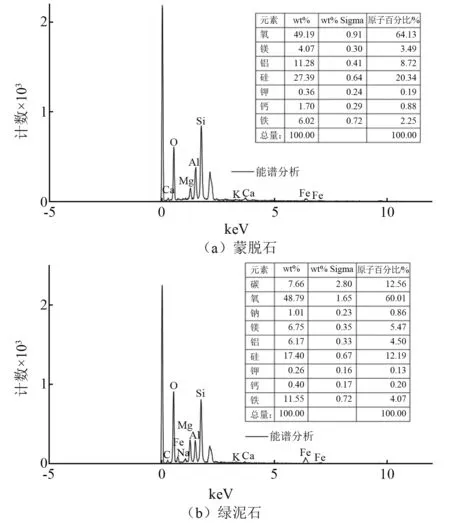
图2 砂岩颗粒表面能谱分析Fig.2 Surface energy spectrum analysis of sandstone particles

依据国际岩石力学学会标准，选用长径比为0.5的试样进行冲击试验，试样直径为50 mm，高度为25 mm，试样的端面平整度经过精细打磨符合规范要求(即平整度在0.02 mm公差范围内)，如图3所示。同时在制取试样过程中剔除表面有明显缺陷及超声波检测波速异常的试样，降低试验结果的离散性，红砂岩的基本物理力学参数，如表2所示。

图3 砂岩试样Fig.3 Sandstone sample

表2 红砂岩基本物理参数Tab.2 Basic physical parameters of red sandstone

冻结红砂岩样品的制备：首先，将制备好的样品置于105 ℃的干燥箱中干燥24 h，然后取出用真空饱和装置进行加压饱和。将饱和样品两端涂上凡士林并用塑料薄膜包裹，然后放置在低温环境箱中，以0.02 ℃/min的恒定冷却速度缓慢冷却，达到设定温度后，稳定48 h，便可获得冻结红砂岩样品。而在SHPB冲击试验中，为减小试件与空气之间的温度交换，控制试样温度处于恒定状态。通过控制冲击试验过程的时间来进行控温，从冻结试样取出到冲击试验结束，整个过程控制在10 s内，即可实现对冻结试样温度的可控，进而减小试验的误差。

1.2 测试装置及工作原理

试验采用φ50 mm高强度合金钢质SHPB试验系统，如图4所示。该系统由长冲击杆(子弹0.5 m)、入射杆(3.0 m)、透射杆(2.5 m)、测速系统、超动态应变仪、瞬态波形采集存储系统和数据处理系统组成，其中杆件系统参数为： 密度7 800 kg/m3、纵波波速5 190 m/s、弹性模量210 GPa。

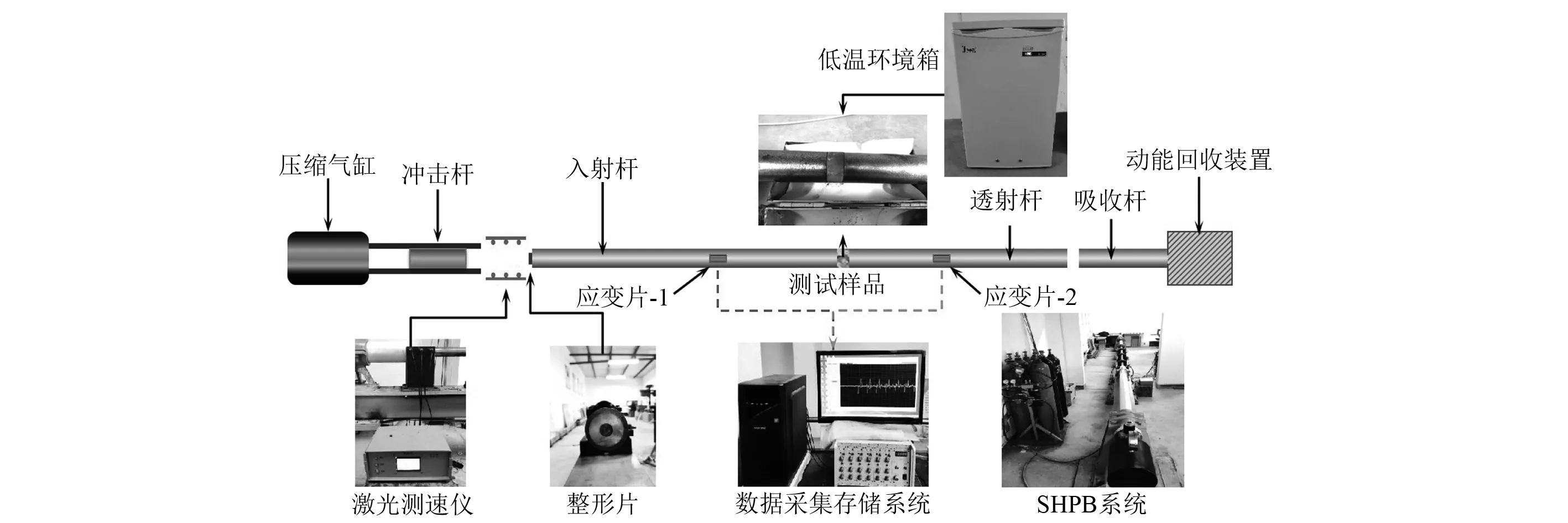
图4 SHPB试验系统Fig.4 SHPB test system

SHPB试验系统的基本原理是基于弹性杆中一维应力波假设和应力均匀性假设。试验中超动态应变仪对粘贴在入射杆和透射杆上的应变片信号值进行采集和存储，通过在入射杆端头粘贴带圆孔紫铜滤波片，过滤掉高频震荡波，使得波形由矩形波转变为类正弦波，保证了数据采集和处理的有效性和准确性，然后根据三波法计算公式，计算得出试样的应力、应变和应变率，如图5所示。其计算公式为

(1)

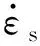
1.3 试验方案

由于在实际工程中不同冻结时间段的冻结温度不同，同时还存在岩体与冻结管距离不同导致冻结温度不同，故确定人工试验冻结温度为-5 ℃，-10 ℃，-15 ℃，-20 ℃以及对照温度常温25 ℃。同时，根据图1实际工程中冻结壁受冲击特征示意图以及前期多次试冲试验，确定了以1.6 m/s，2.4 m/s和3.2 m/s作为正梯度冲击速度。为保证正梯度冲击试验后，试样不发生完全破坏能够进行核磁共振试验，以试样的临界破坏作为本试验研究的破坏准则。不同冻结温度试样正梯度冲击后的形态如图6所示，能够满足核磁共振试验要求。

在冲击试验前，首先对每个饱和试样进行核磁共振检测，获得每个试样的初始T2谱曲线，然后开始进行不同冻结温度下正梯度冲击试验，由于在低温冻结试样内存在冰体会对核磁检测结果产生影响，无法准确获得试样内部孔隙结构的变化，故每次冲击后将试样放入饱和器内恢复常温饱和状态，再进行核磁共振试验，及时对冲击后试样孔隙的变化进行检测，检测完成后再将试样置于低温环境箱中进行冻结，为下次冲击做准备，以此顺序交替进行，直至试验结束。试验方案流程图，如图7所示。

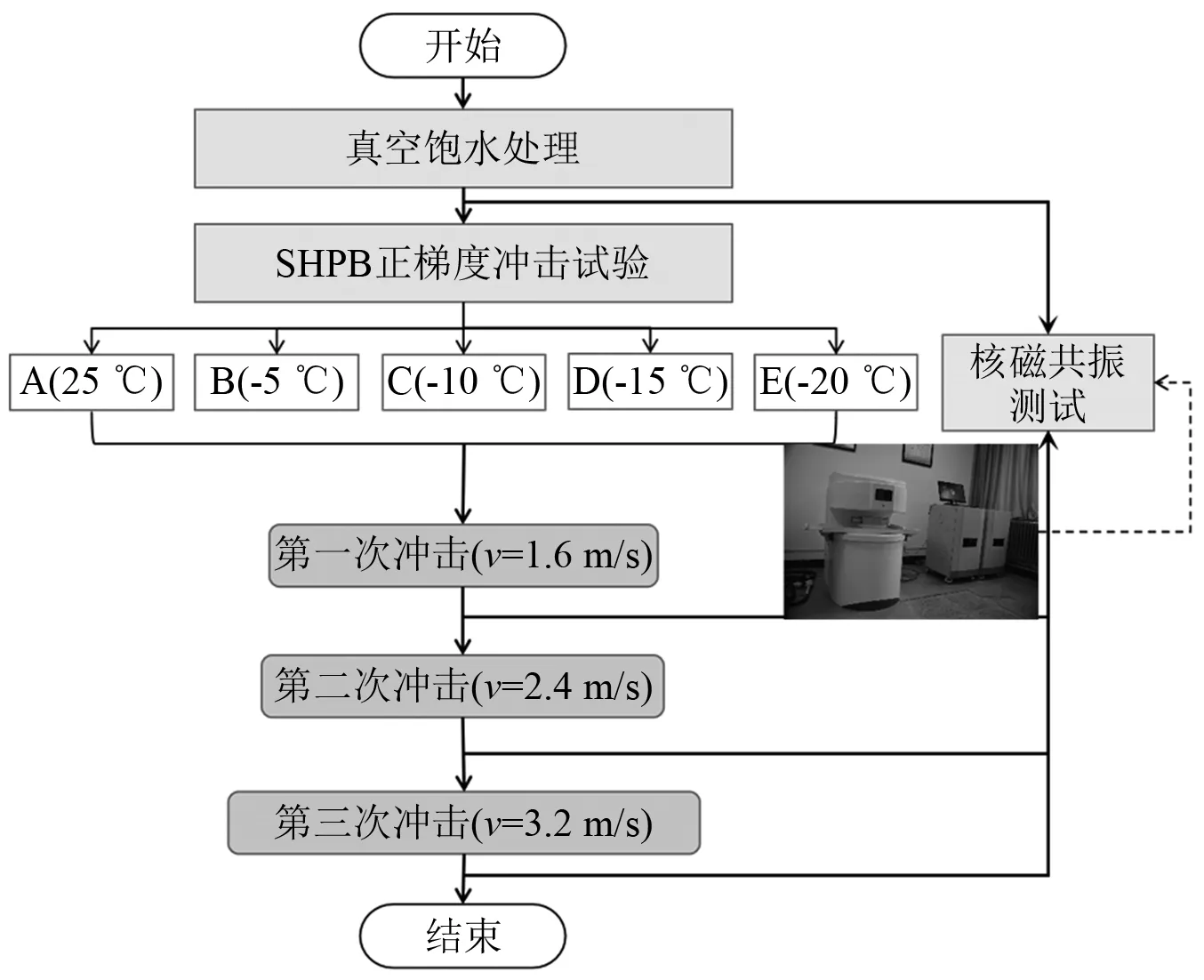
图7 试验方案流程图Fig.7 Flow chart of test scheme

2 试验结果

2.1 力学特征分析

2.1.1 应力-应变曲线特征

根据“三波法”原理，对采集到的有效数据进行解算，根据解算结果得到不同冻结温度下的红砂岩在正梯度冲击作用下的应力应变曲线，如图8所示。

由于在正梯度冲击下SHPB冲击红砂岩应力-应变曲线特征相似，因此以-10 ℃试样的应力应变曲线为例进行说明。其曲线特征大致可分为线弹性阶段、屈服阶段和卸载破坏阶段3个阶段，如图8所示。

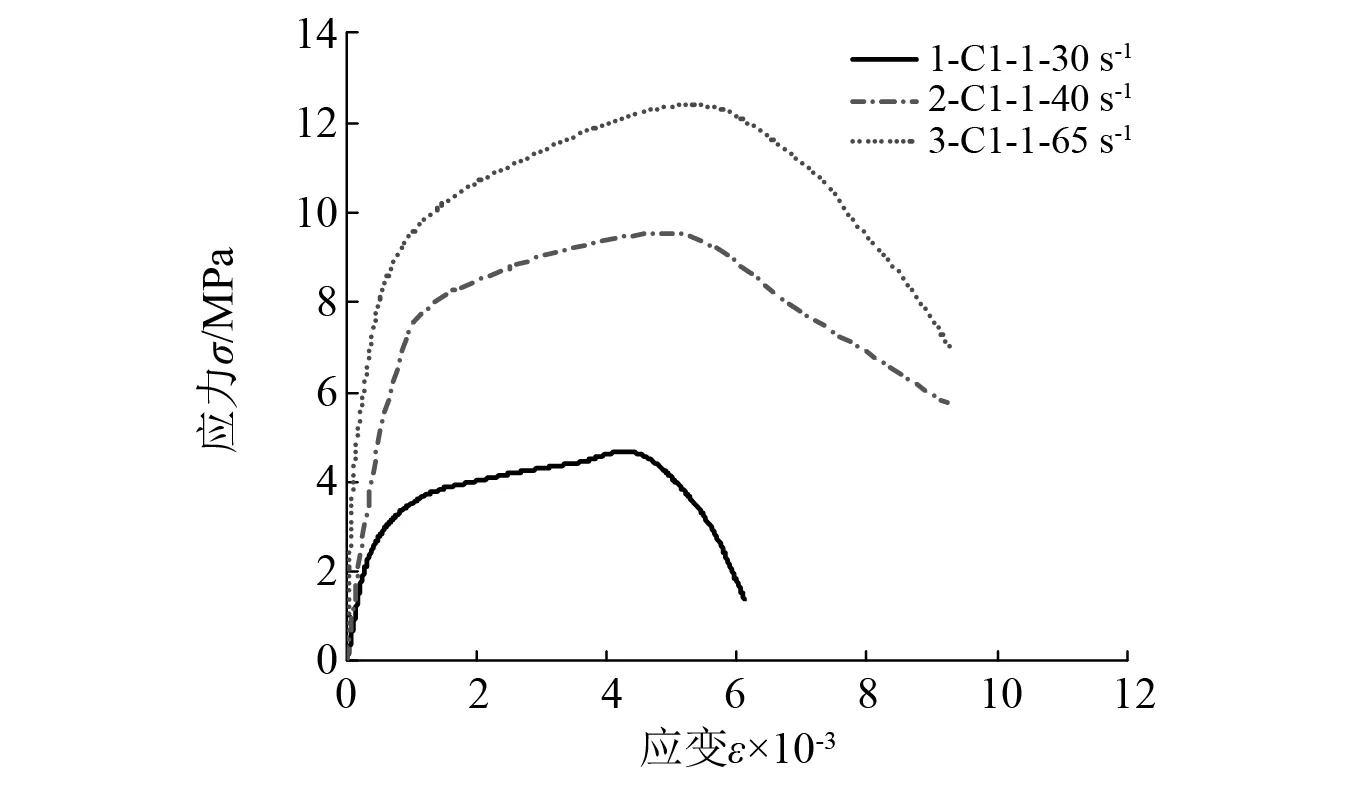
图8 正梯度冲击下-10 ℃试样动态应力-应变曲线Fig.8 Dynamic stress-strain curve of -10 °C specimen under positive gradient impact

线弹性阶段，与静载作用曲线相比，冻结状态下弱胶结砂岩的压密阶段几乎不存在，呈现出显著的线性上升段，线弹性阶段及裂纹稳定扩展阶段变化率更迅速，应力幅值变化迅速，在极短时间内弱胶结砂岩内部应力超过颗粒和胶结物质的强度，使得红砂岩初始弹性模量大，体现出一种较高的冲击韧性。

屈服阶段，在连续动载荷作用下，应力-应变曲线从初始弹性阶段的快速上升段开始出现明显下弯，曲线切线斜率显著低于初始加载阶段，该阶段试样内部微裂隙在应力波的作用下，经历了从出现缓慢增加到稳定扩展，再到部分较大扩展微裂隙相互贯通形成主裂纹的过程，使得试样在此应变率冲击下达到峰值强度点。

卸载破坏段，随着应变的增长，红砂岩应力呈快速下降趋势，其内部宏观破裂面增多，变形加快。

2.1.2 应力与应变率关系

本文研究的峰值应力为不同应变率冲击下对应的最大应力，并非为冲击破坏对应的破坏应力。因此依据正梯度下红砂岩动态应力-应变曲线，将红砂岩在动态冲击下的各项参数进行分析汁算，得到正梯度冲击下不同温度红砂岩试样的动态峰值应力参数，根据数据绘制了正梯度冲击下不同温度红砂岩动态峰值应力与应变率之间的关系，如图9所示。

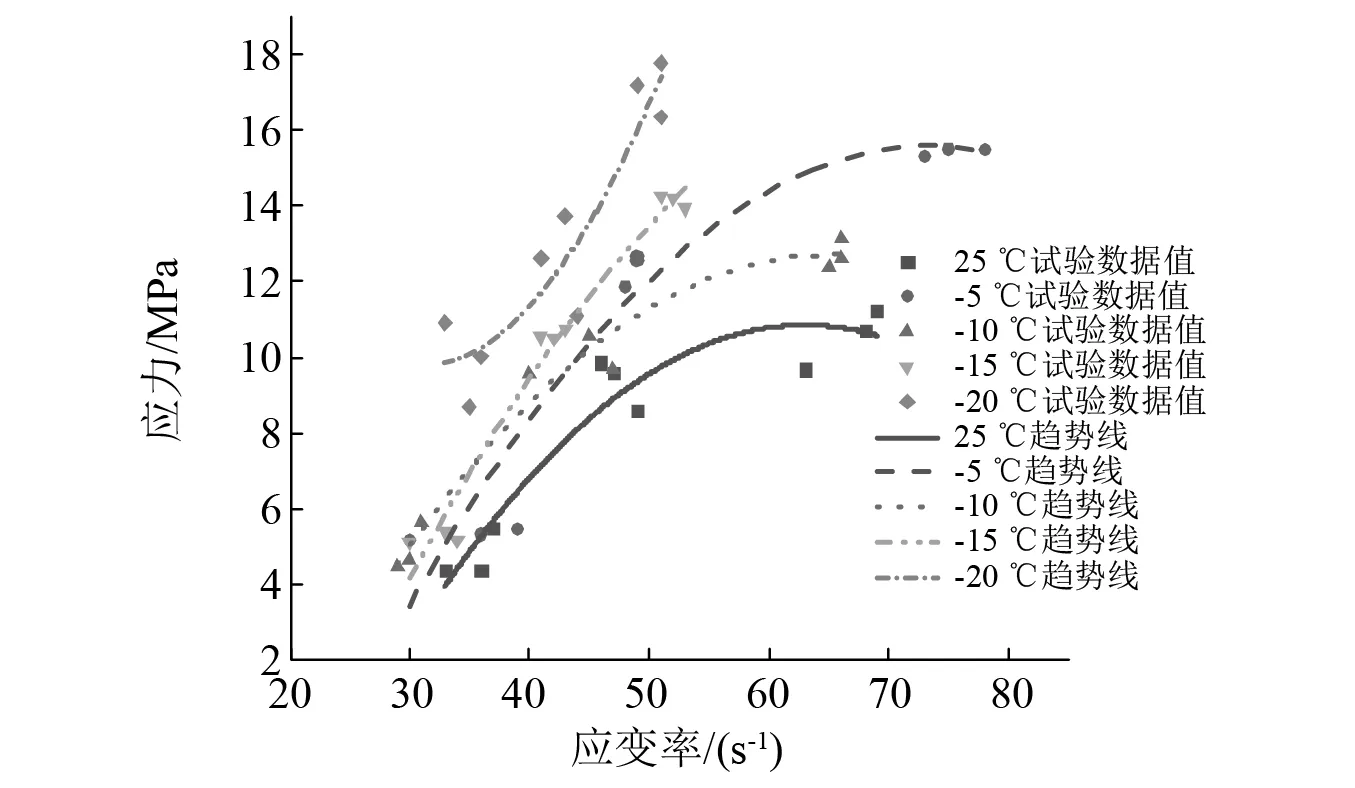
图9 正梯度冲击下不同温度红砂岩应力与应变率关系Fig.9 Relationship between stress and strain rate of red sandstone at different temperatures under positive gradient impact

由图9可知，不同冻结温度的红砂岩在梯度冲击载荷作用下整体的动态峰值应力随应变率的升高而加强，具有明显的应变率相关性。

在低应变率范围内即30～35 s-1，25～-15 ℃的峰值应力相近，范围在4.75～5.32 MPa，但-20 ℃的峰值强度要高于其他温度，这主要是在此温度条件下，岩石基质和冰介质发生固-固相变收缩引起的强度增大所致。

当冻结红砂岩在低应变率冲击后，再进行中应变率冲击，其范围为42.00～48.67 s-1，发现-5 ℃的峰值应力增幅最高，介于-10 ℃和-15 ℃，而在-15～-20 ℃的红砂岩，其峰值应力增幅则小于-5 ℃，这说明-5 ℃与-10 ℃之间由于未冻水含量的减少，冰体的增加对冻结红砂岩造成劣化，以提高强度的形式抵抗变形，而随着温度的继续下降，冰体的强度得到加强，故在-15 ℃时峰值应力要高于-5 ℃。

在中应变率冲击作用后进行较高应变率冲击，由试验可知在高应变率冲击作用下应变率随温度的降低呈现先升高后降低最后趋于平稳的趋势，温度效应明显，故红砂岩峰值应力将受到温度效应和应变率效应共同作用，当温度高于-10 ℃时，应变率效应发挥主导作用，红砂岩峰值强度随应变率的升高而增强，但增加趋势减缓，同时在-5 ℃时出现较高的应力增幅，说明在此温度下试样以扩大损伤来抵抗冲击。

2.1.3 应变与应变率关系

根据试验数据绘制了梯度冲击下不同温度红砂岩动态峰值应变与应变率之间的关系，如图10所示。

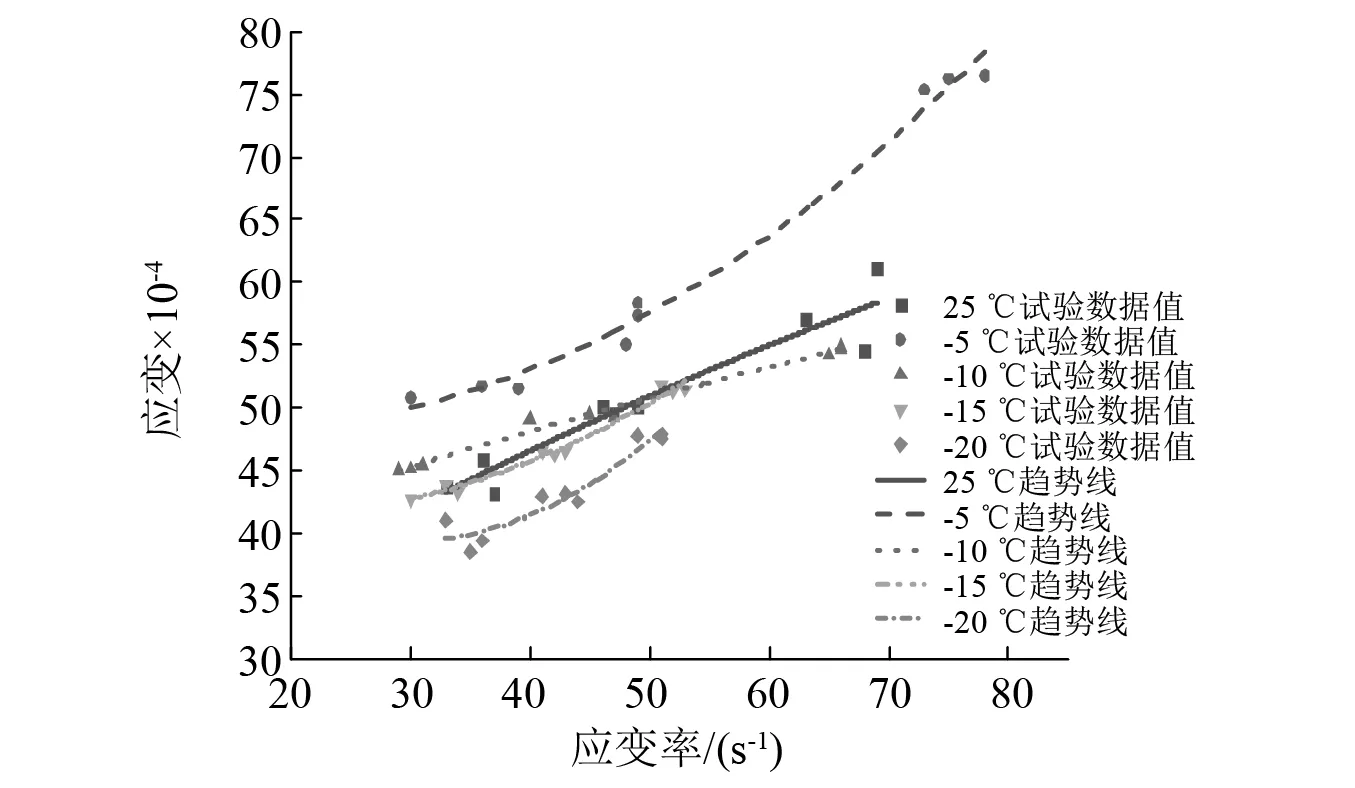
图10 不同冻结温度下应变与应变率关系Fig.10 Relationship between strain and strain rate under different freezing temperatures

峰值应变是衡量岩石变形的重要指标，其表征岩样在峰值强度的变形能力。从图10中对比不同冻结温度发现，以常温25 ℃趋势线为分界线，红砂岩峰值应变的变化趋势明显分为两个阶段：

在分界线上方，随着冲击应变率的升高，-5 ℃试样的峰值应变呈快速增长并达到最大值，由0.005 13增长到0.007 6，增幅高达48.15%。在分界线下方，即冻结温度在-10～-20 ℃时，随着冲击应变率的升高，峰值应变的增长趋势逐渐放缓，同时随着冻结温度的降低，峰值应变呈递减趋势，最终峰值应变由-10 ℃的0.005 46下降到-20 ℃的0.004 78，下降幅度为12.45%，-20 ℃试样的最终峰值应变较-5℃降低幅度高达37.1%。表明冻结红砂岩在峰值强度下的抵抗变形能力增强，同时试样的脆性破坏特征明显提升。

2.1.4 动态弹性模量与应变率关系

不同冻结温度下动态弹性模量与应变率的关系曲线，如图11所示。

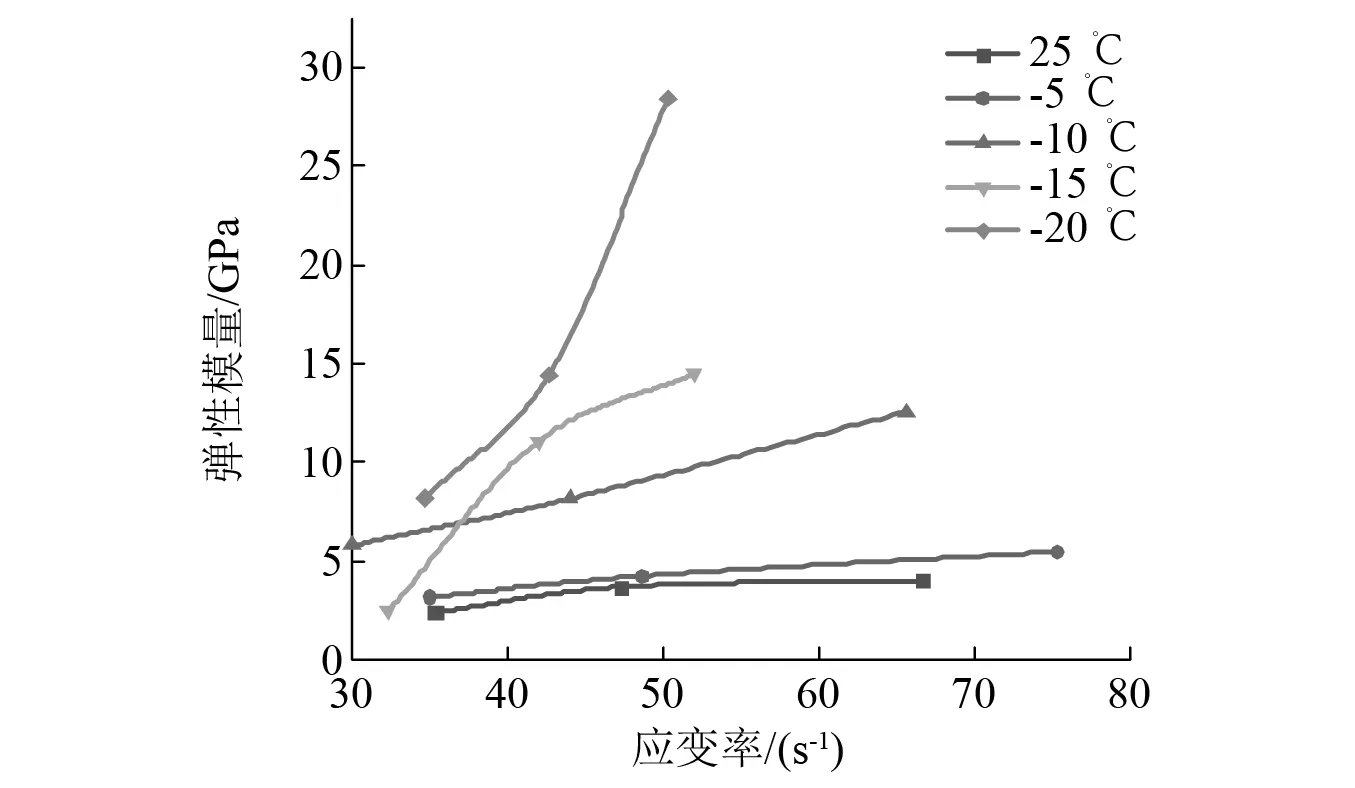
图11 动态弹性模量与应变率的关系Fig.11 Relationship between dynamic elastic modulus and strain rate

由图11可知，不同冻结温度下红砂岩的静态弹性模量介于0.997 5～7.423 5 GPa，与梯度冲击载荷作用下对比发现，红砂岩的动态弹性模量显著提高，在低应变率范围内即(30.00～35.33 s-1)，动态弹性模量是静态弹性模量的1.1倍～2.4倍；在中应变率范围内即(42.00～48.67 s-1)，动态弹性模量是静态弹性模量的1.83倍～3.71倍；在高应变率范围内即(50.00～75.33 s-1)，动态弹性模量是静态弹性模量的2.37倍～4.03倍，表明红砂岩材料的弹性模量具有显著的应变率敏感性。

2.1.5 冻结温度与应变率的关系

正梯度冲击下冻结温度与应变率的关系，如图12所示。由图12可知：随着冻结温度的降低，在第1次低速率冲击作用下，应变率在-10 ℃之前呈现下降趋势，下降幅度为17.77%，之后又由30 s-1上升到34.67 s-1，上升幅度为15.57%；在第2次中速率冲击作用下，应变率整体呈下降趋势，下降幅度为14%；在第3次高速率冲击作用下，应变率先上升在-5 ℃达到最大值75.33 s-1，上升幅度为13%，然后应变随温度的降低呈现下降趋势，由75.33 s-1下降到50.33 s-1，下降幅度高达49.67%。

上述现象表明冻结红砂软岩在低、中速率冲击作用下，应变率不随冻结温度的改变而发生明显变化，温度效应不显著，而在进行高速率冲击时，应变率随冻结温度的下降变化明显，对温度具有较强的敏感性，温度效应显著。

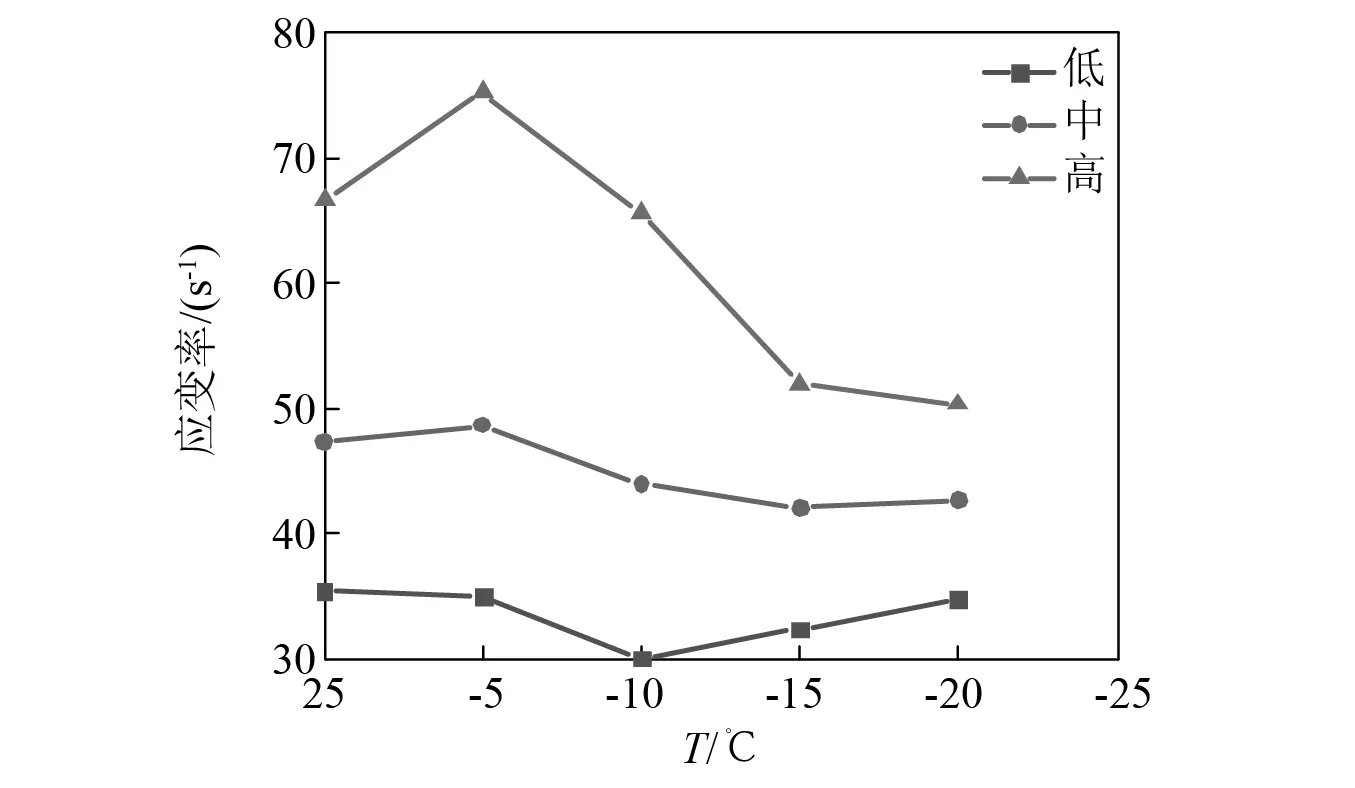
图12 正梯度冲击下冻结温度与应变率的关系Fig.12 Relationship between freezing temperature and strain rate under positive gradient impact

2.2 正梯度冲击下冻结红砂岩的损伤效应

2.2.1 T2谱分布分析

由核磁共振原理可知，核磁共振横向弛豫时间T2主要由岩石孔隙的表面积与体积之比决定，因此T2谱曲线可以直观反映岩石内孔隙大小与数量的变化情况。T2谱曲线中横坐标越大，代表相应孔隙尺寸越大，纵坐标则反映此尺寸下孔隙的数量，即孔隙大小和数量均与T2谱坐标呈正相关。通过分析T2谱曲线，可以得到岩样孔隙尺寸及其数量的变化规律。

由核磁共振测试得到的T2谱曲线形状可知，按照谱峰变化和对应孔隙直径将试样内部孔隙类别大致分为小孔隙、中孔隙及大孔隙共3种，通过3种等级孔隙对应谱峰变化情况来反映本试验中饱水冻结红砂岩在梯度冲击下的孔隙大小改变状况，进一步的可以知道试样内部损伤变化规律，如图13所示。

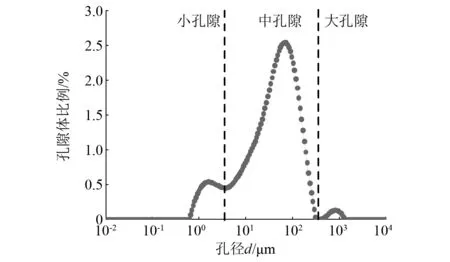
图13 未冲击未冻结试样的孔隙分布图Fig.13 Pore distribution of non impacted and non frozen samples

由正梯度冲击T2谱曲线可知，每个类别的孔隙在正梯度冲击作用过程中变化情况不尽相同，下面根据图14分别对不同孔径的变化情况进行描述与分析。

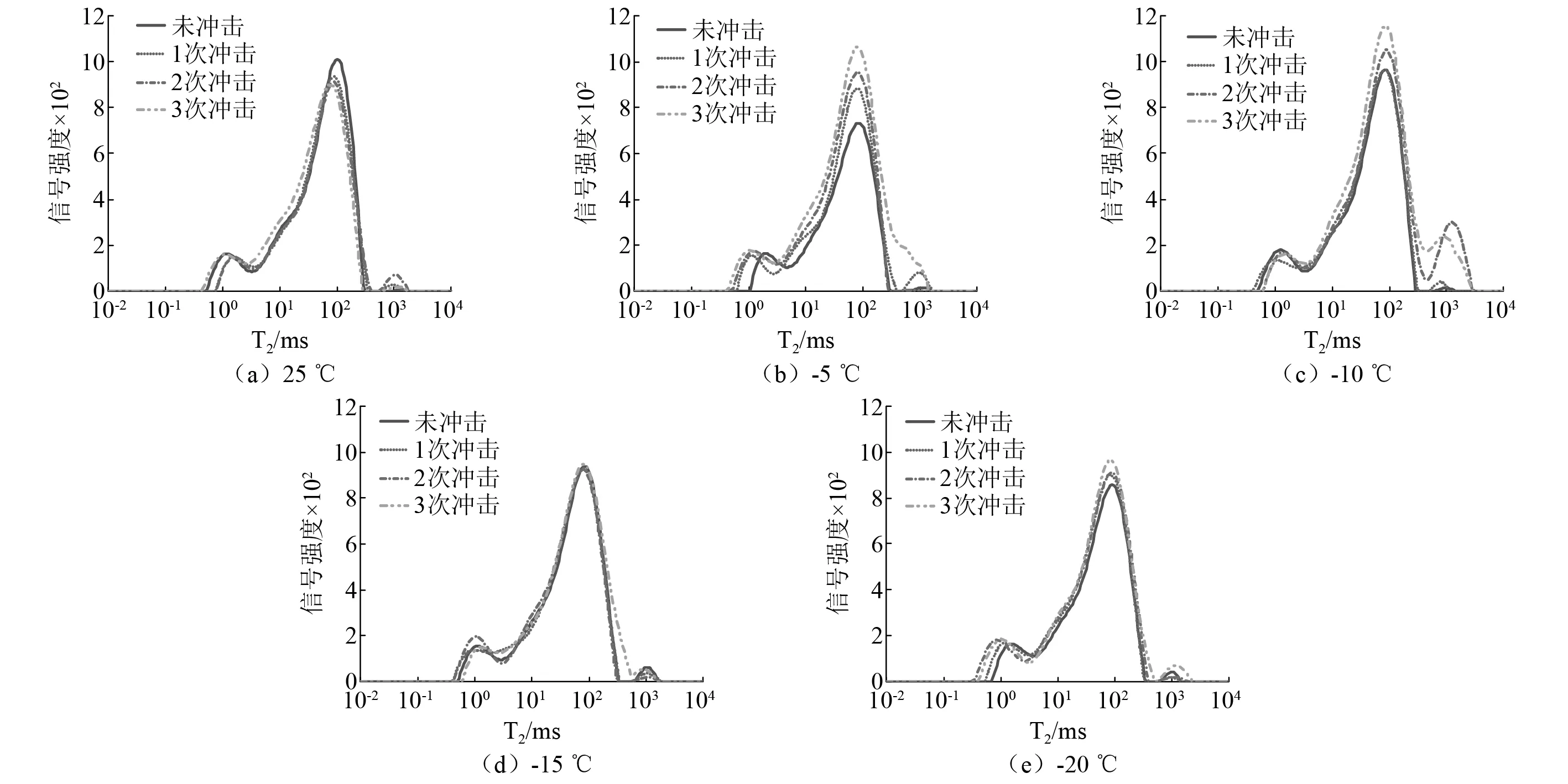
图14 正梯度冲击下红砂岩T2谱曲线Fig.14 T2 spectrum curve of red sandstone under positive echelon impact

小孔隙发展状况，在温度由常温25 ℃下降到-10 ℃过程中，代表小孔隙的谱峰表现为向左移动且峰值变大，温度越低此现象越明显，说明小孔隙孔径减小但数量增多；-15℃和-20℃小孔隙谱峰左移且峰值变小，可见在正梯度冲击下，冻结温度的降低对饱和红砂岩小孔隙的发展变化影响较大。

各温度试样代表中等孔隙的谱峰变化同小孔隙一样表现出明显的温度差异，-15～-20 ℃温度内，试样谱峰峰值的增长趋势，明显弱于在-5～-10 ℃内的试样，说明在-10 ℃出现拐点。随着冻结温度的降低，在拐点温度前中等孔隙数量显著增加，而拐点温度后，中等孔隙数量增幅显著下降，说明梯度冲击对中孔隙的形成影响最大。但由图14可知，全部谱峰横坐标相对原位置没有发生较大变化，表明正梯度冲击对中等孔隙孔径无明显影响。

对比不同温度试样代表大孔隙的谱峰变化情况，发现25 ℃，-5 ℃及-10 ℃试样谱峰峰值均显著提高并右移，而-15 ℃和-20 ℃大孔隙呈现小幅波动，表明饱和红砂岩在正梯度冲击作用下，在温度由25 ℃下降到-10 ℃过程中，大孔隙增多并发生扩展，孔径变大，而在冻结温度由-15 ℃下降到-20 ℃过程中，大孔隙增幅明显低于-10 ℃，且孔隙扩展较为稳定，说明-10 ℃为孔隙变化拐点。

2.2.2 T2谱面积分析

T2谱曲线的形态反映了岩石中孔隙的尺寸和数量的分布特征，曲线和横向弛豫时间轴的积分面积与岩石中孔隙数量成正相关。不同冻结温度红砂岩正梯度冲击前后核磁共振面积变化，如图15所示。

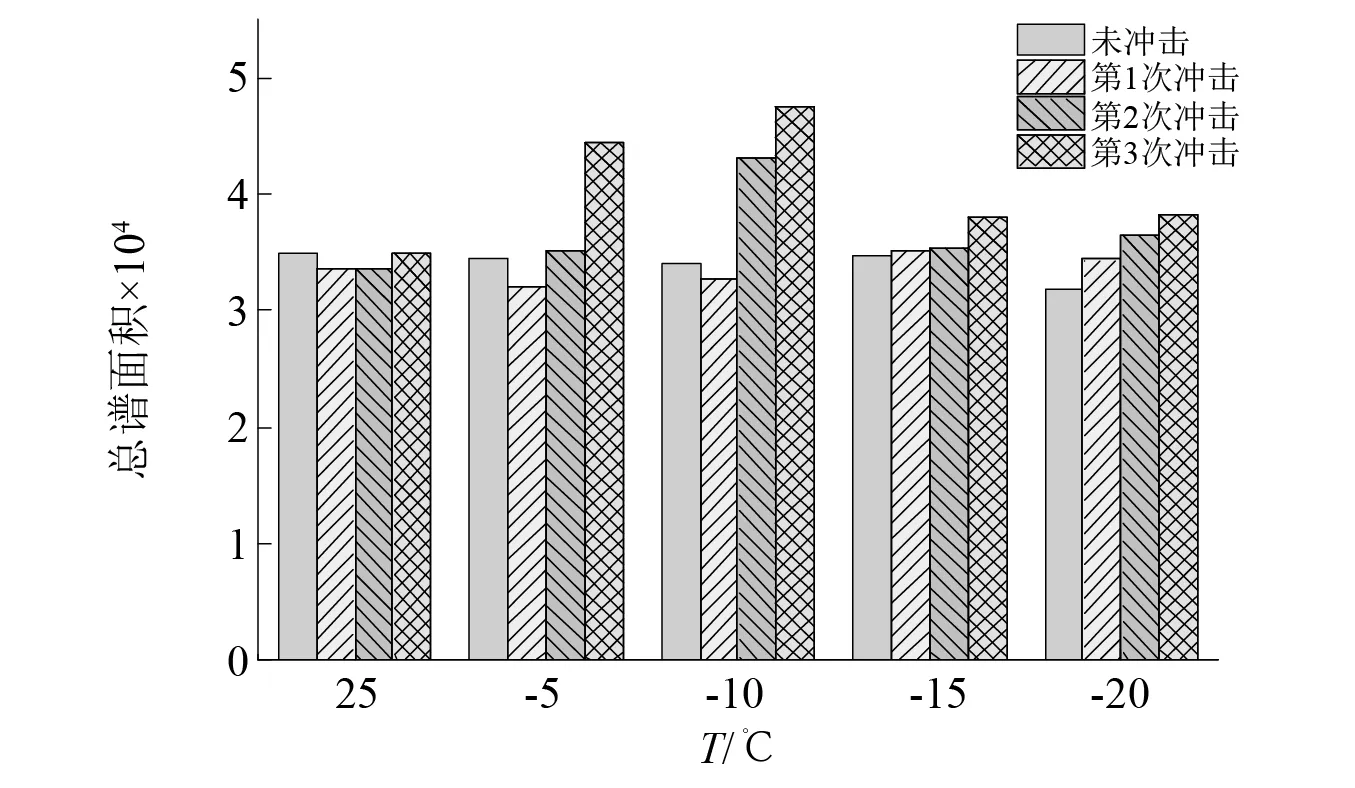
图15 不同冻结温度红砂岩正梯度冲击前后核磁共振面积分布图Fig.15 Nuclear magnetic resonance area distribution of red sandstone before and after positive gradient impact at different freezing temperatures

由图15可知，在正梯度冲击下各温度试样在初始总谱面积基本相同的条件下，25 ℃，-5 ℃及-10 ℃试样在经历第1次冲击后总谱面积均呈现小幅降低，降低幅度分别为3.78%，6.81%和3.86%，表明在较低的应变率撞击下，试样内部小孔隙得到压缩，从而造成孔隙数量减少，而在-15 ℃和-20 ℃时，试样总谱面积相对增加了1.5%和8.07%，孔隙数量不减反增，与其他温度等级相比表现出明显的温度效应。随着正梯度冲击的继续进行，各温度试样总谱面积均呈上升趋势，从小、中、大孔隙谱峰比变化情况可知：总谱面积的增加一方面来源于新孔隙的生成；另一方面主要是由于小、中孔隙在正梯度冲击作用下逐渐发育贯通成为大孔隙。对比正梯度冲击完成前后发现，-5 ℃及-10 ℃试样谱峰总面积与初始情况相比均有较大幅度增加，增幅分别为29.3%和39.57%，在-15 ℃和-20 ℃区间内，谱峰总面积增长较为稳定，增幅分别为9.8%和20.4%，发现在-10 ℃时达到最大值出现拐点，表明正梯度冲击在-10 ℃之前，冻结温度的降低起到劣化作用，造成试样内孔隙数量增多。

2.2.3 正梯度冲击作用下冻结红砂岩损伤演化规律

在进行不同梯度冲击试验过程中，为探究冻结红砂岩的梯度损伤演化规律，故在冲击试验前后结合核磁共振试验对试样在细观方面的损伤进行识别，试验测得的正梯度冲击作用下的孔隙度数据，如表3所示。

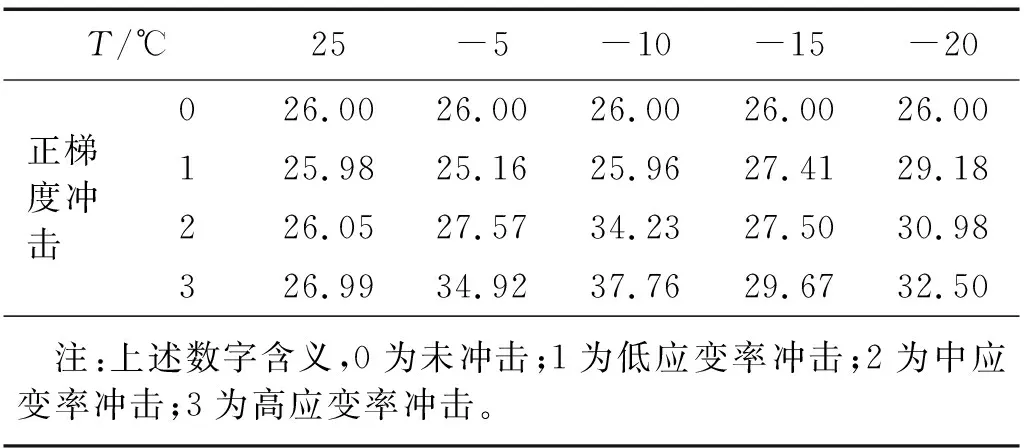
表3 正梯度冲击下不同冻结温度红砂岩的孔隙度变化Tab.3 Porosity changes of red sandstone under different freezing temperatures under positive echelon impact

对于天然岩石类材料来说，在成层历史中及天然环境作用下，材料内部本身就存在缺陷和劣化区，这就是岩石材料的初始损伤。而在施工开采过程中，岩石在受到不同梯度冲击作用下产生的损伤为扰动损伤，也可称为梯度损伤。本节主要依据不同梯度冲击前后的孔隙度变化，对冲击后产生的损伤进行定义，进而分析研究不同梯度冲击后，不同冻结温度红砂岩的损伤演化规律。

Kachanov和Rabotonov提出了用连续度Ψ来定义材料扰动后的损伤变量D，其中

(2)

D=1-Ψ

(3)

式中：VD为扰动损伤后有效承载面积；V为损伤前承载面积；Ψ为连续度。

根据损伤变量的定义方法，本节主要利用核磁共振试验测得的梯度冲击前后孔隙度来定义连续度Ψ和损伤变量D。在梯度冲击试验前，首先对加压饱和的红砂岩进行初始孔隙度n0的测量，然后再对每次冲击后的孔隙度n进行量测。由于梯度冲击试验中对于试样总体积V0的影响较小，故假设冲击前后试样总体积V0不变，则有

V1=V0(1-n0)

(4)

VB=V0(1-n)

(5)

式中：V1为未冲击时试样内部颗粒所占体积；VB为冲击后试样内部颗粒所占体积。

将式(4)和式(5)分别代入式(2)和式(3)，可以得到梯度冲击作用下红砂岩的连续度和损伤变量

(6)

(7)

式(7)为不同梯度冲击作用下，孔隙度与损伤变量的关系。其中D为标量，当D=0时为初始状态，即无损状态，当D=1时为完全损伤状态。

将表3数据代入式(7)，计算得出正、负梯度冲击后损伤变量变化趋势图，如图16所示。

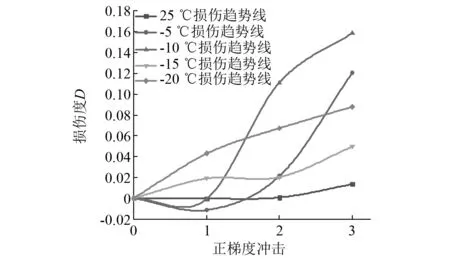
注：上述横坐标轴数字含义，0为未冲击；1为低应变率冲击；2为中应变率冲击；3为高应变率冲击图16 正梯度冲击下不同冻结温度红砂岩损伤度变化趋势Fig.16 Change trend of damage degree of red sandstone at different freezing temperatures under positive gradient impact

由图16可知：第1次冲击后，在25～-10 ℃的温度内具有“负损伤”，即与初始损伤相比，损伤减小，表明在冻结温度为-10 ℃之前，岩样中存在未冻结的孔隙，在低应变速率的影响下，导致该区域的孔隙压实；随着冲击速度增加(即应变率逐渐升高)，当冻结温度在-5～-10 ℃时，岩石样品的损伤趋势大大增加，最终在-10 ℃时损伤达到最大；对于-15～-20 ℃内的冻结温度，正梯度冲击下岩样的损伤趋势呈均匀增长趋势，发现正梯度冲击下-20 ℃冻结温度的损伤程度高于-15 ℃。结合应力-应变曲线可以看出，-20 ℃损伤程度的增加主要用于应力增长和强化。

3 结 论

本文采用直径为φ50 mm的霍普金森压杆试验装置对冻结红砂岩进行了正梯度冲击压缩试验。研究正梯度冲击荷载下，冻结红砂软岩的动力特性。同时，在冲击试验过程中，利用核磁共振技术对正梯度冲击前后的样品进行了损伤统计，研究了冻结红砂岩在梯度冲击下的损伤演化规律。主要结论如下：

(1) 正梯度冲击与低温耦合作用下红砂岩的动态应力应变曲线特征可分为3个阶段——线弹性上升阶段、屈服阶段和卸载破坏阶段。在正梯度冲击下，冻结红砂岩的动态抗压强度、应变和动弹性模量具有明显的应变率相关性。

(2) 在正梯度冲击下，应变率与冻结温度的关系如下——在低、中速率冲击下，冻结红砂软岩的应变率随冻结温度的变化不显著，温度效应不显著。而在高速率冲击下，应变率随冻结温度的降低先增大后减小，且温度效应显著，正梯度冲击的拐点温度出现在-10 ℃，表明在低、中速率扰动冲击后，在较高速率的冲击下，试样发生内部损伤，导致应变率峰值提前。

(3) 根据正梯度冲击前后各温度样品的T2谱曲线和核磁共振测试中孔隙面积的变化，得出以下损伤演化规律——在25～-10 ℃内，随着冻结温度的降低，中、大孔隙和孔隙总谱面积显著增加，而在-15～20 ℃内则呈小幅稳定增加。

(4) 通过孔隙度定义的损伤演化规律，发现正梯度冲击下的损伤程度和扩展演化速率较高，拐点温度出现在-10℃，随着冻结温度的降低，在拐点温度之前，试样损伤演化速率加快，在拐点温度之后，则相反。