轴向力作用下过屈曲Timoshenko梁与Euler-Bernoulli梁的自由振动特性对比

井 洁， 毛晓晔， 丁 虎， 陈立群

(上海大学 力学与工程科学学院 上海市应用数学和力学研究所，上海 200444)

在道路交通、桥梁建筑、工程机械等领域，梁是普遍使用的结构。在已有经典梁理论中，Euler-Bernoulli梁理论忽略了横向剪力和切应变的影响，适用于细长结构。但是，这种简化会高估梁的弯曲刚度，因此，Timoshenko梁理论被提出来以研究短粗结构。即使是细长梁，在考虑高阶振动时，剪切变形的影响依然是不可忽略的，因此Timoshenko梁理论相比Euler-Bernoulli梁理论具有更高的精确性，尤其是对于动力学而言[1]。

在实际应用中，梁往往会承受轴向应力，这会对梁的动力学特性产生较大影响。许醇义[2]通过数值计算推证轴向力对弯曲振动自振频率的影响，发现各种支承梁由于承受轴向压力使刚度减小，频率随压力的增大而减小；杜绍洪[3]通过有限差分法求解了简支梁的横向自由振动问题，构造出求解四阶非稳态线性偏微分方程的差分隐格式，数值试验表明构造的隐格式绝对稳定并且具有很高的精度阶。Ma等[4]研究了轴力作用下多裂纹梁的模态及疲劳寿命分析，发现轴向力除了会改变梁的动力学特性，还会加速梁的疲劳破坏； Karimi等[5]研究了梁在随机轴力作用下的非线性振动分析，结果表明梁的平均和均方值都是时间的函数，这意味着梁的侧向位移是一个非平稳过程； Li等[6]系统地研究轴向受压Timoshenko梁的弯曲、屈曲和自由振动问题，在模型中引入了表征变形过程中轴力方向的过渡参数，结果表明，过渡参数对轴向加载梁的弯曲、屈曲和自由振动均有显著影响，频率随轴向压力的增大而减小，这对轴力方向的确定具有重要意义； Liu等[7]研究了非连续梁在不同轴向载荷和连接弹簧刚度作用下的挠度和振动频率，结果表明，随着连接弹簧刚度的增大，连接弹簧的挠度呈指数级减小，振动频率呈指数级增加。这些研究都表明，轴向力的存在会对梁的动力学特性及使役性能产生重要影响。

当轴向压力继续增加，一阶固有频率会减小至零，结构发生过屈曲现象[8]，梁会变成本质非线性结构，其动力学响应会产生更复杂现象，例如在低频区域产生超谐波共振[9]。因此，研究梁承受过轴向力导致的过屈曲是很有必要的。诸多学者已经对不同结构的屈曲现象进行了研究，比如李世荣等[10]研究了加热弹性梁在热过屈曲构形附近的自由振动，数值结果表明，梁在未屈曲时，各阶频率都随升温而单调下降。在过屈曲后则相反；Li等[11]采用Timoshenko梁理论和高阶剪切变形梁理论对柱形结构稳定性进行了研究，重点分析了Engesser’s和Haringx’s假设对屈曲的影响。结果表明，两种假设对强剪切刚度柱的屈曲载荷影响不大，而对弱剪切刚度柱的屈曲载荷影响显著。平动弹簧刚度对屈曲载荷的影响比转动弹簧刚度更明显。Ziane等[12]考察了矩形空心截面的简支钢梁，考虑到较大的扭转和截面畸变，利用同伦摄动法研究了后屈曲非线性路径，得到了外力偶引起横向扭转屈曲临界值的闭合表达式。Einafshar等[13]针对薄壁梁的轴向弯曲屈曲、后屈曲和几何非线性分析，提出了一种高效的一维有限元模型。为验证模型的有效性，进行了各种屈曲、后屈曲和非线性弯曲试验，证明了所提薄壁梁稳定性和几何非线性分析公式的有效性和准确性。Ferreira等[14]研究复合材料蜂窝梁的屈曲和后屈曲分析，随着腹板长度的增加，腹板屈曲模式由局部屈曲变为后屈曲。这种效应增加了临界整体剪切。因此，相比非屈曲结构，屈曲结构的动力学研究更具挑战，目前还在不断发展完善。

对于梁结构，常用Timoshenko梁模型及Euler-Bernoulli梁模型。滕兆春等[15]基于Euler-Bernoulli梁建模，研究了过屈曲轴力下的横向自由振动。各阶频率在过屈曲前随轴向压力的升高而单调下降，这是由于轴向压力的存在使梁的挠度增加，相当于减少了梁的刚度，使固有频率降低，过屈曲附近一、二阶频率随轴向压力的升高而单调增加。而刘吉源等[16]利用瑞雷法得到任意边界条件下的Timoshenko梁固有频率泛函方程，对两边均为固定端约束的情形建立了频率方程，并分别讨论了轴向力、转动惯量和剪切变形对频率方程解的影响，进而得到相应的固有频率。Ding等[17]首次发现了转动惯量和剪切变形对超临界轴向运动梁横向振动的影响；王乐等[18]从Timoshenko梁平衡方程出发，建立了轴力作用下Timoshenko梁自由振动偏微分方程，给出了求解Timoshenko梁固有频率的方程，探究了其横向振动特性，计算结果表明轴向压力对最低阶频率的影响最大，阶次越高影响越小。Khodabakhsh等[19]采用非线性Timoshenko梁模型对功能梯度材料柔性输流管道的后屈曲和非线性振动进行了分析研究。数值结果证明了在分析短粗功能梯度材料管道时考虑截面旋转惯性和剪切变形的重要性，特别是对于初始振幅较高的刚性材料，再次说明将Timoshenko梁模型用于短粗梁研究的必要性。以上这些研究都肯定了Timoshenko梁模型在描述短粗结构的精确性，但是，对于其在过屈曲轴力作用下，其共振频率如何变化，特别是在基本过屈曲构形附近各阶频率如何变化，目前还缺少定量的研究结果。

本文基于Timoshenko梁建模，讨论了在轴力过屈曲时梁的自由特性，并且与Euler-Bernoulli梁进行了对比分析。应用广义哈密顿原理建立控制方程[20]，用Galerkin法离散成多自由度系统。在过屈曲状态下，得到了梁的固有频率，并讨论了参数影响。

1 数学模型对比

圆形截面梁如图1所示，材料密度为ρ，长度为L，横截面直径为D，两端受简支支撑。图1中：x和y分别为轴向和径向坐标；v(x,t)为梁的横向位移；t为时间。截面绕中性轴的转动惯量为I，剪切模量为G，杨氏模量为E，泊松比为μ，且受轴向力P作用，参数值如表1所示。

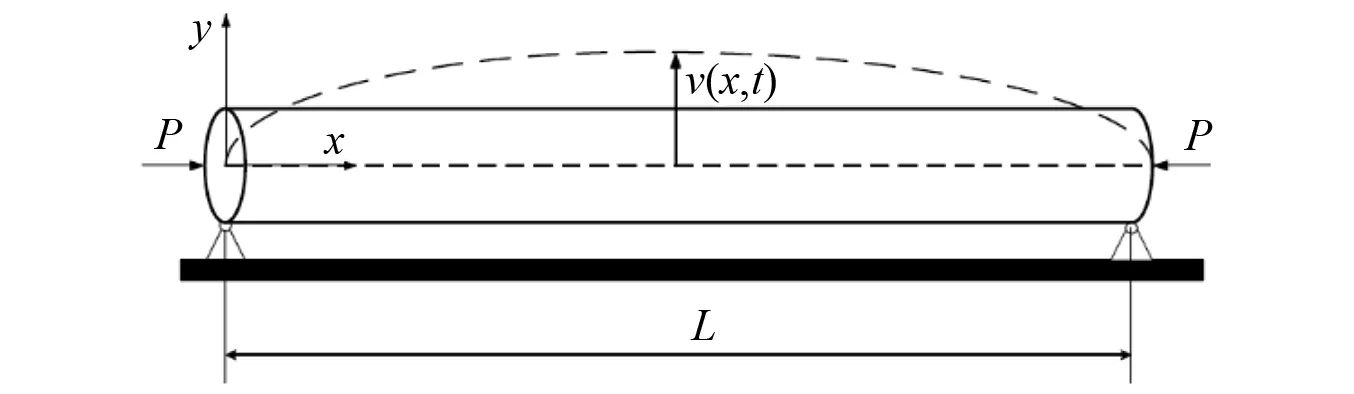
图1 梁的物理模型Fig.1 Physical model of the beam

表1 梁物理参数Tab.1 Physical parameters of the beam

1.1 Timoshenko梁模型控制方程

对于短粗梁，参考Tan等[21]的控制方程建立过程，采用Timoshenko梁模型进行建模基于广义Hamilton原理，导出Timoshenko梁横向振动偏微分-积分控制方程

(1)

式中：A为梁的横截面积；v(x,t)为梁的横向位移；x或t前面的逗号为对x或t的偏导数；ks为圆形截面剪切修正因子,其表达式为

(2)

根据表1中泊松比的取值，将其代入式(2)，ks则可取为0.89。

两端简支边界条件为

(3)

1.2 Euler-Bernoulli梁模型控制方程

同样，参考Tan等研究中应用Euler-Bernoulli梁理论建立控制方程的过程，可推导得到Euler-Bernoulli梁横向振动控制方程

(4)

简支边界条件如下

(5)

对比控制方程式(1)和式(4)可以看出Timoshenko梁模型为二阶偏微分方程组，而Euler-Bernoulli梁模型则为四阶偏微分方程。因此，Timoshenko梁在横向和转角两个广义坐标上分别具有两个边值条件，而Euler-Bernoulli梁仅在横向广义坐标上具有4个边值条件。

2 过轴向力静态屈曲分岔对比

2.1 简支梁屈曲非平凡位形解析解

考虑屈曲失稳引起的屈曲非平凡位形，由于其与时间坐标无关，忽略方程式(1)中的时间项，得到静态控制方程

(6)

两端简支边界条件为

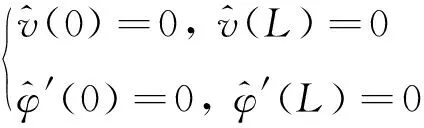
(7)

通过式(6)和式(7)，得到Timoshenko梁屈曲非平凡位形解析解

(8)

同理可以得到Euler-Bernoulli梁的屈曲非平凡位形解析解

(9)

式中，k为任意非零整数，在此将k取为1，研究第一阶屈曲非平凡位形。

两种梁模型的第一阶屈曲非平凡位形对比图，如图2所示。由于屈曲非平凡位形关于零平衡位形轴对称，因此本文只考虑正屈曲非平凡位形。图2中：实线表示Timoshenko梁的横向位形和转角；点线表示Euler-Bernoulli梁的横向位形；Pcr为梁的临界轴向力。图2选取的过屈曲轴向力为临界轴向力的1.1倍。从图2可知，Euler-Bernoulli梁的横向位形大于Timoshenko梁。

图2 两种梁模型的屈曲非平凡位形(P=1.1Pcr)Fig.2 The buckling non-trivial configuration of two beam models (P=1.1Pcr)

2.2 简支梁屈曲非平凡位形稳定性

考虑第一阶屈曲非平凡位形，不考虑外激励及阻尼，从截断方程中得到第一阶截断方程，最终得到第一阶非平凡位形上的未扰系统

(10)

其中

(11)

将该方程改写为状态方程，提取自治系统Jacobian矩阵，当矩阵特征值λ存在正实部时，一阶位形不稳定。与Euler梁一阶位形的稳定性对比，如图3所示。当轴向力达到屈曲值后，两种模型的一阶位形都稳定，但临界轴向力存在差异，显然Timoshenko模型因为考虑了截面转动，刚度稍弱于Euler-Bernoulli模型，临界屈曲发生地更早。

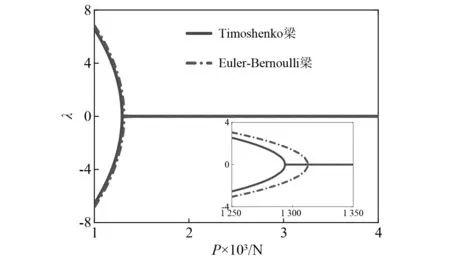
图3 一阶屈曲非平凡位形的稳定性Fig.3 Stability of first-order buckling non-trivial configuration

高阶屈曲非平凡位形与Euler-Bernoulli模型一致，都不具有稳定性。

2.3 参数对轴向力静态屈曲的影响

两种梁模型的临界轴向力可以通过式(8)和式(9)得出

(12)

为了更清晰地描述两种模型之间的差异，定义了临界轴向力的相对误差

(13)

式中：Pcr-E为Euler-Bernoulli梁模型的临界轴向力；Pcr-T为Timoshenko梁模型的临界轴向力；RPL为两种梁模型临界轴向力随长度变化的相对误差，同理RPD为两种梁模型临界轴向力随梁截面直径变化的相对误差。梁越细长，临界轴向力越小，且Euler-Bernoulli梁因刚度大于Timoshenko梁，其临界轴向力总是大于Timoshenko梁，如图4(a)所示。随着梁长的增加，这种差异越来越小，说明细长结构可采用Euler-Bernoulli梁理论。由图4(a)可知，在梁长大于0.1 m时，两种梁模型临界轴向力随长度变化的相对误差小于10%，而在图4(b)所取的范围内，临界轴向力随梁截面直径变化的相对误差总是小于1.5%，说明两种梁临界轴向力对长度变化的敏感程度大于对截面直径的敏感度。

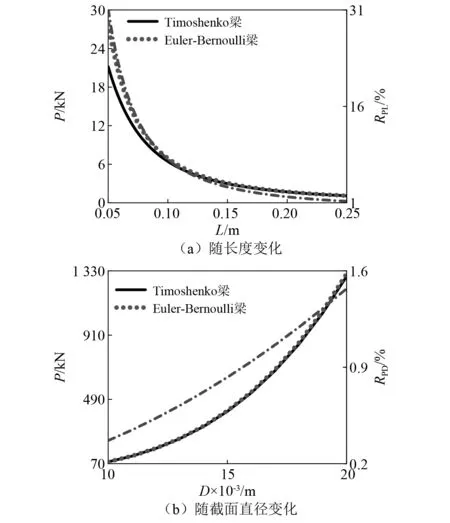
图4 两种梁模型临界轴向力的比较及相对误差Fig.4 Comparison of critical axial forces and relative errors for two beam models

两种梁模型的中点位移和轴向力之间的关系，如图5所示。由图5可知，引起Timoshenko梁平衡分岔的轴向力要小于Euler-Bernoulli梁的轴向力。但Timoshenko梁的平衡变形要大于Euler-Bernoulli梁的平衡变形。此外，当梁较短或较厚时，两种梁模型之间的差异更明显。

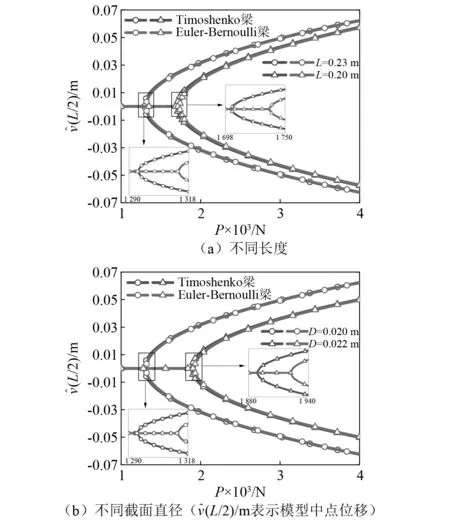
图5 两种梁模型随轴向力的变化情况Fig.5 Variation of two beam models changing with axial force

3 过轴向力固有频率对比

3.1 Galerkin截断

对于过轴向力下的简支Timoshenko梁，由式(1)推导得到自由振动控制方程

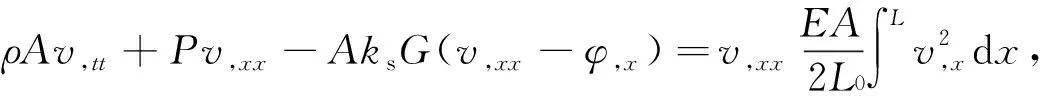
(14)

对式(14)进行坐标代换

(15)

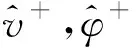
(16)

式(16)存在非线性项，对其进行局部线性化，得到

(17)

设式(17)的解为如下形式，仅保留前m阶

(18)

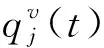
(19)

设权函数为模态函数自身，采用Galerkin法，得到离散的常微分方程系统。基于该离散系统，即可求解屈曲后Timoshenko梁的自由振动固有频率。系统刚度矩阵可写为如下形式：式(20)为屈曲前的刚度矩阵，式(21)为屈曲后的刚度矩阵

(20)

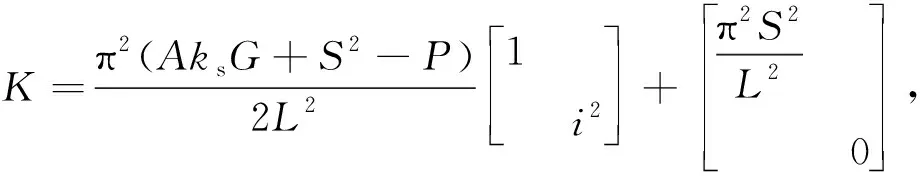
(21)

从式(20)和式(21)可以看出，在屈曲前，高阶频率会受到轴力的影响，而在过屈曲发生后，高阶刚度矩阵分量中不含轴力项，所以高阶频率不随轴力变化。

Galerkin截断得到的，随轴向力变化的前两阶固有频率，如图6所示。由图6中可知，在屈曲发生前，随着轴向力的增加，前两阶固有频率都在减小。但是在屈曲后，随着轴向力的增大，一阶固有频率随之增大，而二阶频率不发生变化。

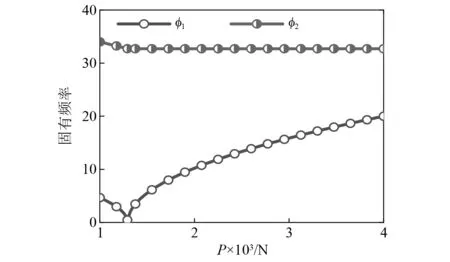
图6 Timoshenko梁的前二阶频率Fig.6 The first-two order frequencies of the Timoshenko beam

此外，基于线性派生系统式(17)，得到了严格意义上的模态，因此截断后广义坐标解耦，模态坐标间不存在能量交换，截断阶数不影响结果的收敛性。因此在接下来的文章中，如无特别说明，都将采用二阶Galerkin截断法对控制方程进行截断降维处理。

3.2 固有频率对比

为了便于展示出两种梁模型的差异，定义前两阶固有频率的相对偏差

(22)

式中：fEi为Euler-Bernoulli梁模型的第i个固有频率；fTi为Timoshenko梁模型的第i个固有频率；Ri为固有频率的误差率。由图7可知，相同参数条件下，两种梁的前两阶固有频率随轴向力的变化趋势定性相同：屈曲前都随轴向力减小；而在屈曲后，一阶频率随轴向力的增大呈增大趋势，二阶频率基本不受轴向力的影响。但在定量上，两者存在区别：由于Timoshenko梁屈曲更早，相同的过轴向力下，其一阶频率大于Euler梁一阶频率。因二阶频率不受过轴向力影响，其二阶频率一直比Euler梁小，且差异要大于一阶频率。

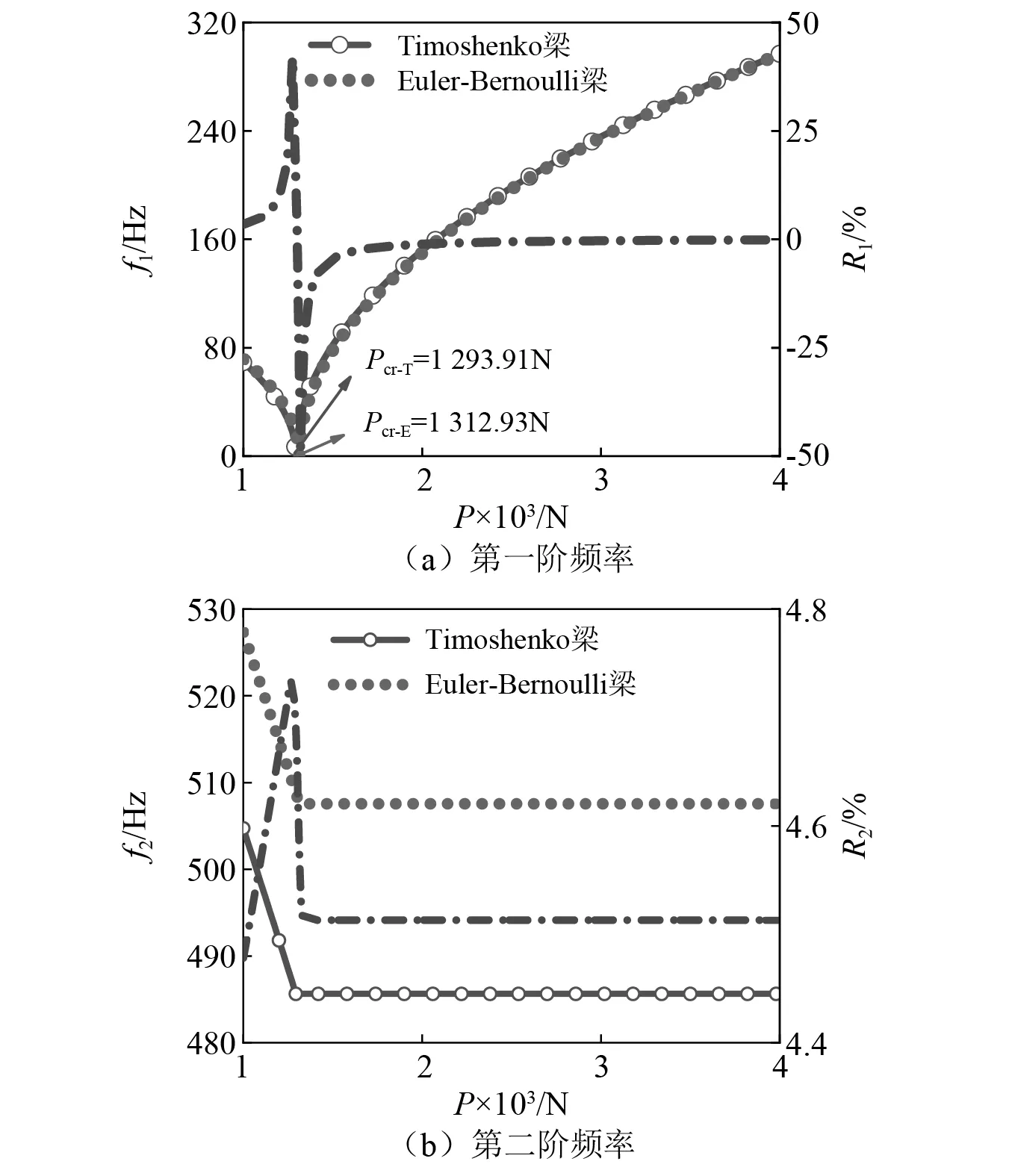
图7 两种梁的前二阶频率对比Fig.7 Comparison of the first-two order frequencies of the two beams

3.3 参数对固有频率的影响

与2.3节一致，不同梁长和截面直径条件下，Timoshenko模型和Euler-Bernoulli模型前二阶频率随过屈曲轴向力的变化，分别如图8、图9所示。见图8(a)和图9(a)，随着梁长的增加，一阶频率差异减小。虽然图示两种梁长的频率存在交叉现象，但将横坐标分别做对应临界轴向力的移轴后，依然是较短的梁比较长的梁具有更高的固有频率。见图8(b)和图9(b)，两种梁模型的第二阶固有频率不随轴向力变化，但Euler-Bernoulli梁的二阶频率总是大于Timoshenko梁的二阶频率。

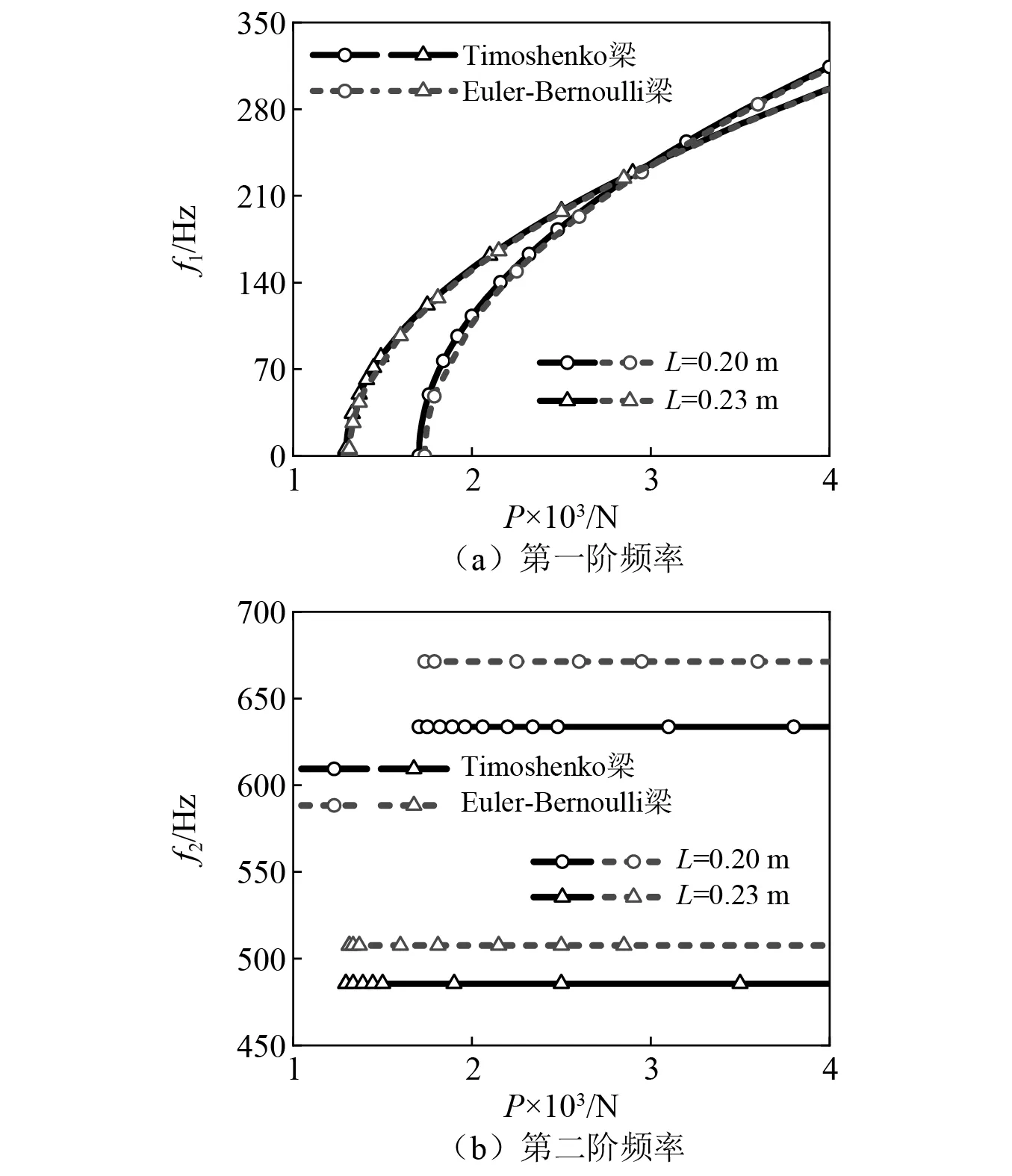
图8 长度不同时两种模型的固有频率对比Fig.8 Comparison of the natural frequencies of the two models with different lengths

同样选取2.3节的参数条件，长细比对固有频率相对误差的影响，如图10所示。图10(a)清楚地表明，随着轴力的增加，两种模型第一阶过轴力屈曲固有频率的相对偏差呈现出减小的趋势，两种模型越来越接近。在轴力大于3 000 N时，第一阶固有频率的相对误差小于1.5%。在同一轴力条件下，长细比越大，固有频率的差值越小。由图10(b)可知，同一长细比条件下，第二阶固有频率的误差不受轴力影响，长细比越大，两种模型第二阶固有频率的相对误差越小。

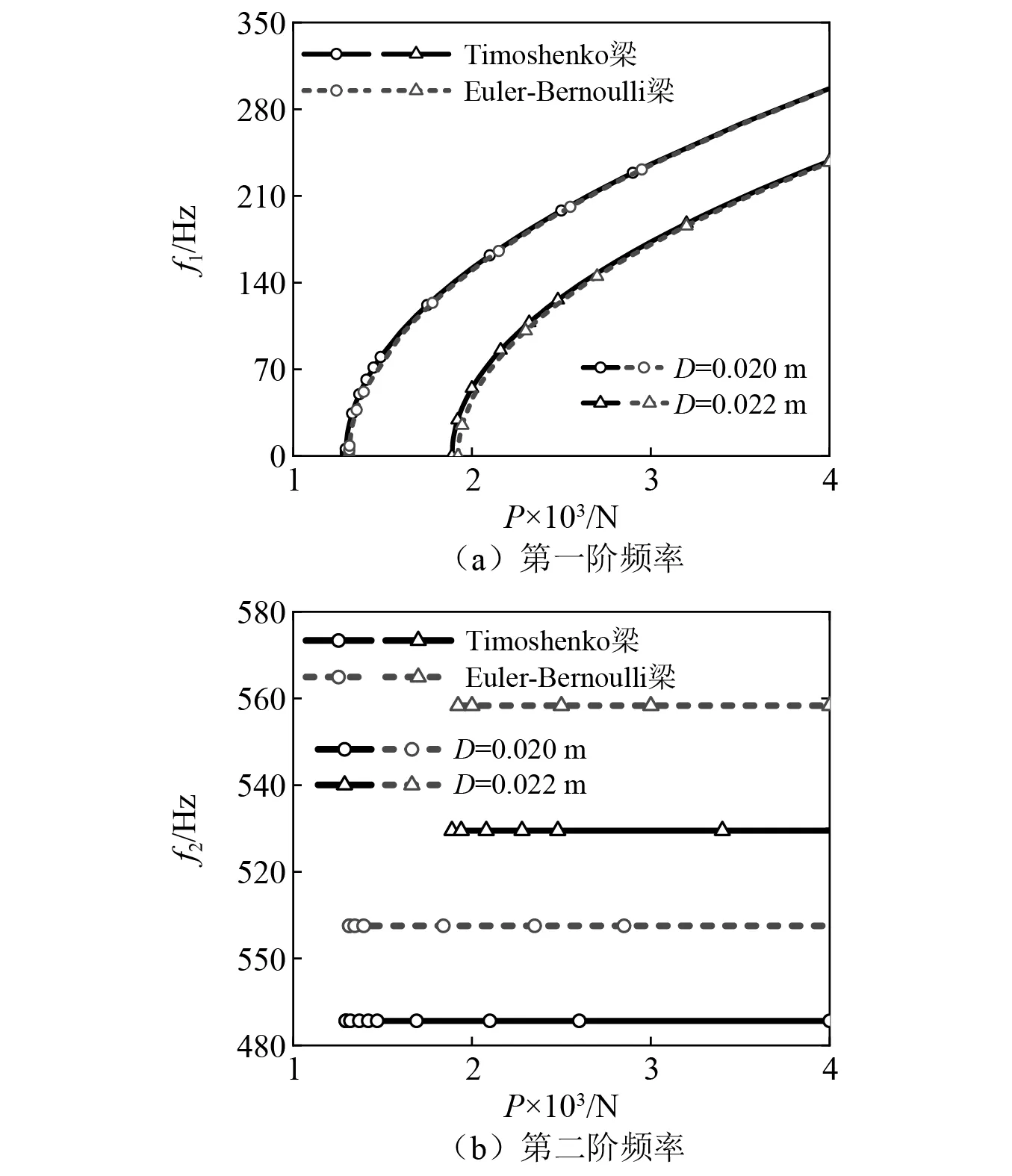
图9 截面直径不同时两种模型的固有频率对比Fig.9 Comparison of natural frequencies of two models with different section diameters

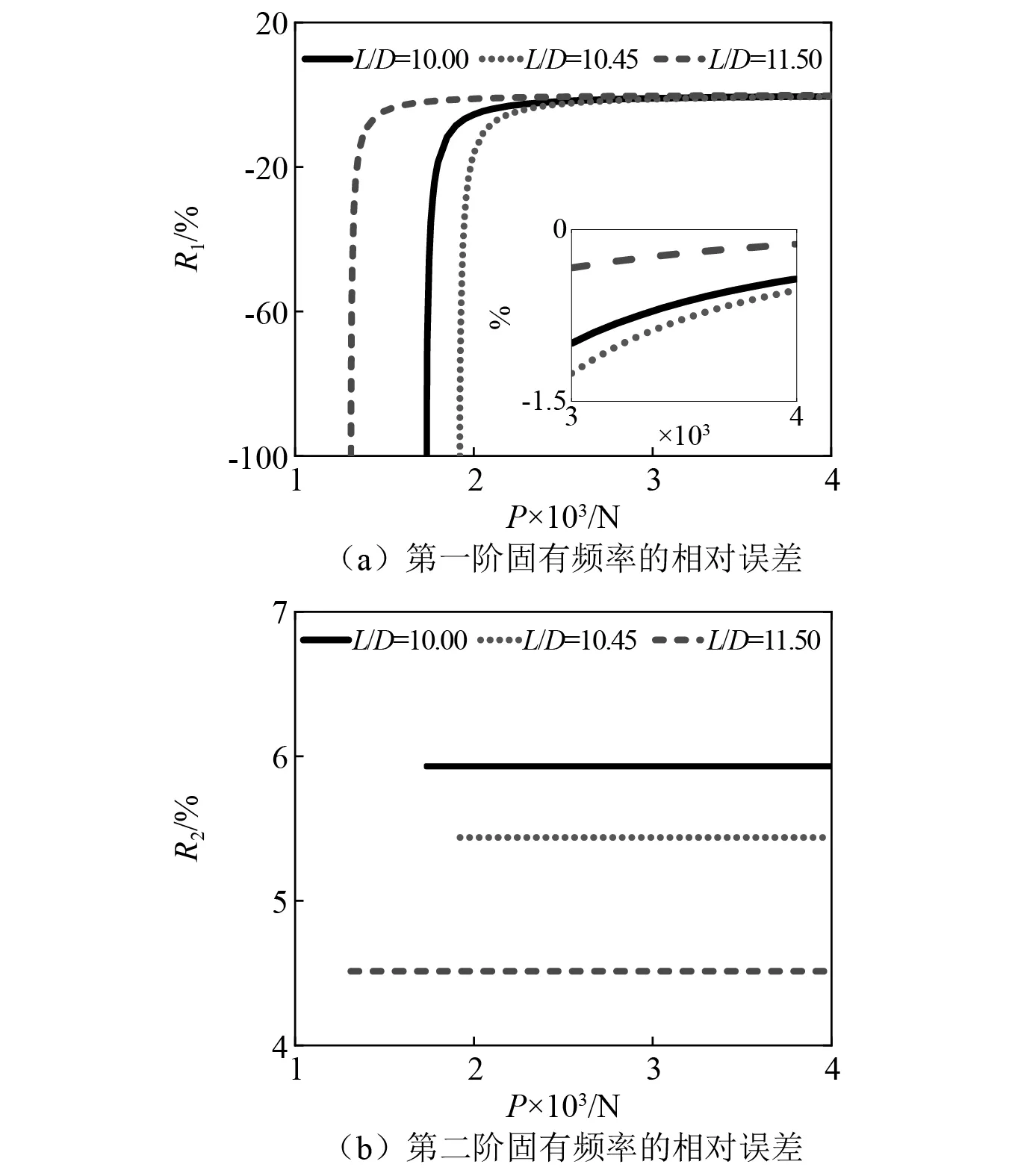
图10 两种模型在不同长细比下前两阶固有频率的相对误差Fig.10 The relative error of the first two natural frequencies of the two models under different slenderness ratios

为详细探讨截面转动对Timoshenko梁刚度的影响，在此分析了不同横向变形下的弯曲势能和剪切势能。在2.1节中已经推导出了简支梁屈曲非平凡位形解析解，如式(8)所示。可见每一个轴力都对应一个屈曲位形，所以在此变为研究不同轴力下的弯曲势能和剪切势能，其表达式为

Ub=∭VσxεxdV,Us=∭VτyxγyxdV

(23)

式中：V为梁的体积；Ub和Us分别为Timoshenko梁的弯曲势能和剪切势能；σx和εx分别为法向应力和法向应变；τyx和γyx为剪切应力和剪切应变。梁的弹性本构关系为

σx=Eεx,τyx=ksGγyx

(24)

应变-位移关系为

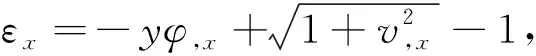
(25)

式中，y为横截面上任意点距中性面的距离。以上均可参考Tan等研究中的建模过程。

由图11可知，弯曲势能和剪切势能随轴力的增大均呈增大趋势。但不同的是，弯曲势能是非线性增大，而剪切势能是线性增大。所以剪切势能占总变形势能的比重随轴力的增大而减小，截面转动软化了Timoshenko梁的刚度。即轴力越大，剪切势能占比越小，弯曲势能占比越大，两种模型越接近。这一结论也可以与“图10(a)清楚地表明，随着轴力的增加，两种模型第一阶过轴力屈曲固有频率的相对偏差呈现出减小的趋势，两种模型越来越接近”相互验证。

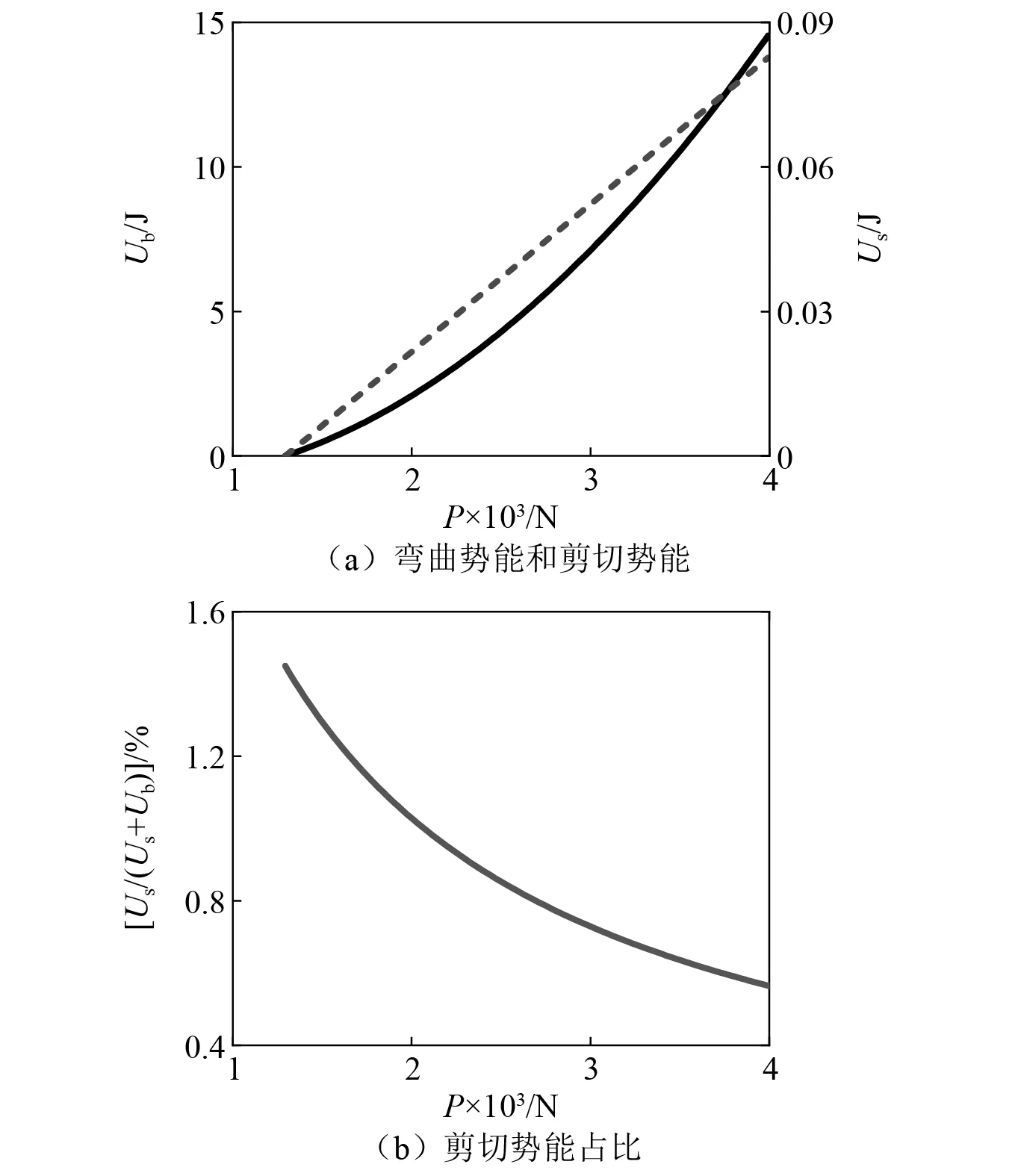
图11 不同轴力下的势能及占比图Fig.11 Potential energy and its proportion under different axial forces

4 结 论

本文研究了轴向力过屈曲的条件下，Timoshenko梁的振动特征，并与Euler梁模型进行对比分析。通过Timoshenko梁模型，建立两端简支条件下屈曲压力、屈曲后位形的解析表达式，并判断一阶位形的稳定性。运用Galerkin截断法计算了梁在轴向力过屈曲条件下的固有频率，确定系统参数的影响，并且对弯曲势能和剪切势能进行分析讨论，得出如下结论：

(1) 与屈曲前固有频率与轴向力的关系相反，在过屈曲发生后，一阶频率随轴向力的增大而增大，二阶及二阶以上频率不随轴向力变化。

(2) 两种梁临界轴向力对长度变化的敏感程度大于对截面直径的敏感度。且Euler-Bernoulli梁过屈曲轴向力比Timoshenko梁大，即Timoshenko梁比Euler-Bernoulli梁更早进入过屈曲状态。

(3) 在屈曲前，Euler-Bernoulli梁的固有频率总是大于Timoshenko梁；在屈曲后，由于临界屈曲发生更早，Timoshenko梁的基频在相同轴向力下总是大于Euler-Bernoulli梁；但将过屈曲轴向力与两种模型相应临界轴向力做归一化处理后，Timoshenko梁基频仍然大于Euler-Bernoulli梁。

(4) 轴力越大，两种梁模型一阶频率相对偏差越小，Timoshenko梁的剪切势能所占比重越小，两种模型越接近。由此可以看出，Timoshenko梁的一部分振动能量存储在截面转动变形中，软化了弯曲刚度，这种软化作用在高阶频率上体现更明显，与Euler-Bernoulli梁相比，高阶频率差异要大于基频。

(5) 对于长细比较大的梁，固有频率差值会越小。进一步说明了将Euler-Bernoulli梁用于细长梁研究、而将Timoshenko梁用于短粗梁研究的合理性。