广义Tikhonov正则化工况传递路径分析

唐中华， 昝 鸣， 张志飞， 徐中明， 晋 杰

(1. 重庆大学 机械与运载工程学院，重庆 400044； 2. 交通运输部公路科学研究院，北京 100088)

工况传递路径分析(operational transfer path analysis，OTPA)是定位与辨识振动噪声问题及传递路径的有效方法[1-2]。相比经典传递路径分析(classic transfer path analysis,CTPA)，工况传递路径分析仅需要不同工况下目标点与指示点的响应数据，不需要拆分系统及测试系统频率响应函数与工况载荷力，从而能够节省实验时间，实验效率较高[3-4]。广泛应用于汽车[5]、高速列车[6-7]及船舰[8]等工程领域。

工况传递路径分析基于传递率函数展开实验，传递率定义为运行工况下目标点响应与指示点响应之间的比值[9]。但在实际工程应用中，指示点响应矩阵通常是病态的[10]，因此工况传递路径分析估计传递率函数矩阵的过程是一个病态的反问题。Tikhonov正则化是处理反问题的有效方法，通过引入正则化矩阵L和正则化参数[11]，可以提高反问题解的准确度。成玮等[12]将Tikhonov正则化引入工况传递路径分析中，仿真与实验结果均表明，相比传统奇异值分解(singular value decomposition，SVD) 法，Tikhonov正则化法所获取的各路径贡献量精度更高，误差更小。Li等[13]提出了一种基于条件数准则的多参数Tikhonov正则化方法来估计传递率函数。实验结果表明多参数Tikhonov正则化法有效提升了工况传递路径分析的精度。但在估计传递率函数矩阵过程中，正则化矩阵为单位矩阵(即：L=I)，此时称为标准Tikhonov正则化。标准Tikhonov正则化经过奇异值分解得到的奇异向量振荡较严重，构成的正则化解准确度较低[14]，会影响各路径贡献量的计算精度。而正则化矩阵可以约束正则化项，并且正则化矩阵可以控制反问题解的基向量的选择，因此正则化矩阵可以选择非单位矩阵[15-16]，此时称为广义Tikhonov正则化。采用一阶偏导矩阵作为正则化矩阵时，结合广义奇异值分解，得到的广义奇异向量振荡幅度较小，因此构成的正则化解准确度更高。Beck等[17]将广义Tikhonov正则化引入图像去模糊中，重构的图像优于标准Tikhonov正则化结果。Gauthier等[18]利用广义Tikhonov正则化进行波束形成声源识别，重构的声源更加清晰，更加接近原始声场。因此，广义Tikhonov正则化是处理反问题更优的选择，但在工况传递路径分析中应用较少。

为提高工况传递路径分析的准确度，将广义Tikhonov正则化应用于工况传递路径分析中。将一阶偏导矩阵作为正则化矩阵，以广义奇异值分解得到的广义奇异向量作为解的基向量，并采用L曲线法选择正则化参数，分析得到各路径的贡献量。最后，在集中质量块模型上进行工况传递路径分析仿真及在一铝板上展开工况传递路径分析实验，验证广义Tikhonov正则化工况传递路径分析方法的有效性。

1 工况传递路径分析

假设一系统为线性时不变系统，根据工况传递路径分析理论，指示点响应矩阵X与目标点响应矩阵Y之间的关系可表示为

Y=XT

(1)

式中，T为传递率函数矩阵。式(1)展开成矩阵形式

(2)

式中：r为目标点个数；n为指示点个数；m为工况数。为了保证指示点响应矩阵X可逆，要求工况数大于等于指示点数，即m≥n。

1.1 奇异值分解

工况传递路径分析，如式(1)，在估计传递率函数矩阵T时，由于指示点响应矩阵X通常是病态的，因此式(1)可看作是一个病态的反问题。奇异值分解常用在反问题求解中。对指示点响应矩阵X进行奇异值分解，有

(3)

式中：U和V分别为左奇异向量ui和右奇异向量vi构成的酉矩阵;VH为V的共轭转置矩阵；Φ为所有奇异值构成的对角矩阵，Φ=diag(φ1,φ2,…,φn)，且有φ1≥φ2≥…≥φn>0，即所有奇异值按降序排列。

于是通过指示点与目标点响应矩阵得到的传递率函数矩阵可表示为

(4)

通过传递率函数矩阵及指示点响应矩阵，即可得到每种工况下每条路径的贡献量，例如工况1下，各路径对目标点1的贡献量为

(5)

由式(4)可知，在求解传递率函数矩阵过程中，当目标点响应Y在测量过程中被噪声ΔY干扰时，较小的奇异值会放大噪声的影响。最大的奇异值与最小奇异值之比φ1/φn定义为矩阵的条件数，反映矩阵的病态程度。当矩阵条件数越大(矩阵病态越严重)，TSVD受误差影响越严重。且根据Hansen和Christensen-Dalsgaard等的研究，随着i的增大，奇异向量ui和vi振荡越严重，因此TSVD的准确度较低，同时影响每条路径贡献量的准确度。为提高其准确度，常用Tikhonov正则化来改善反问题的病态性。

1.2 标准Tikhonov正则化

Tikhonov正则化在最小二乘法的基础上，通过引入正则化项，并通过Lagrange方程将反问题转换为无约束最优化问题，从而求解。其目标函数为

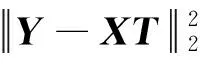
(6)

式中:λ为正则化参数，可通过L曲线选取[19-20]；L为正则化矩阵，通常L=I，即标准Tikhonov正则化。

则标准Tikhonov正则化的解TSTik可表达为

TSTik=(XHX+λ2I)-1XHY

(7)

结合式(4)可得

(8)

式中:ui,vi,φi意义与1.1节中一致，分别为指示点响应矩阵X的奇异向量和奇异值;fi为过滤因子

(9)

用TSTik替换式(5)中TSVD，即可得到每条路径的贡献量。

对于较大奇异值，fi趋近1；而对于较小奇异值，fi<1。因此，较小奇异值的影响可通过fi得到改善。

TSTik通过标准Tikhonov正则化引入了过滤因子fi，其准确度相比TSVD有一定程度的改善，但其仍由指示点响应矩阵X的奇异向量构成，仍然会受奇异向量ui和vi较大振荡的影响。且根据Hansen的研究，虽然奇异向量ui和vi分别为指示点响应矩阵X的列空间和行空间的最佳基向量，但是vi不一定是期望正则化解的最佳基向量。因此，有必要引入非单位矩阵作为正则化矩阵来控制正则化解的基向量选择，进一步提高传递率函数矩阵的准确度。

1.3 广义Tikhonov正则化

式(6)中，当L≠I时，则称为广义Tikhonov正则化。而正则化矩阵L可选择一阶偏导矩阵L1

此时，广义正则化问题可用矩阵对(X，L)的广义奇异值分解(generalized singular value decomposition，GSVD)来分析

(10)

γi=ci/si

(11)

最后可得广义Tikhonov正则化解TGTik

(12)

(13)

2 仿真分析

为了验证广义Tikhonov正则化在工况传递路径分析中的有效性，在九自由度集中质量块模型[21]上开展工况传递路径分析，如图1所示。

图1 九自由度模型Fig.1 Nine degrees of freedom model

该模型共包含9个质量块，各质量块之间通过弹簧和阻尼单元连接，各质量、刚度与阻尼参数如表1所示。仅考虑各质量块的平动自由度，忽略转动自由度。

表1 质量、刚度和阻尼参数Tab.1 The parameters of mass, stiffness and damping

若将被动部分的质量块M1当作目标点，则主动部分的振动可通过3条路径传递至M1，即路径35，路径46和路径78。用F=10 N(如图2)分别激励质量块M9，M5，M6和M8形成4组工况用来估计工况传递路径分析的传递率函数矩阵，分别记为工况一、工况二、工况三和工况四，保证工况数大于路径数。

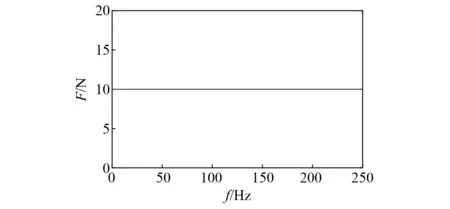
图2 仿真激励载荷Fig.2 The load for simulation

2.1 经典传递路径分析

经典传递路径分析虽然耗时长，工作量大，但其准确度较高，因此将经典传递路径分析所得的各路径贡献量当作准确值[22]，来验证广义Tikhonov正则化在工况传递路径分析中的有效性。

经典传递路径分析第一步需要将系统拆分，如图3所示，然后获取被动部分的频响函数H13，H14和H17。

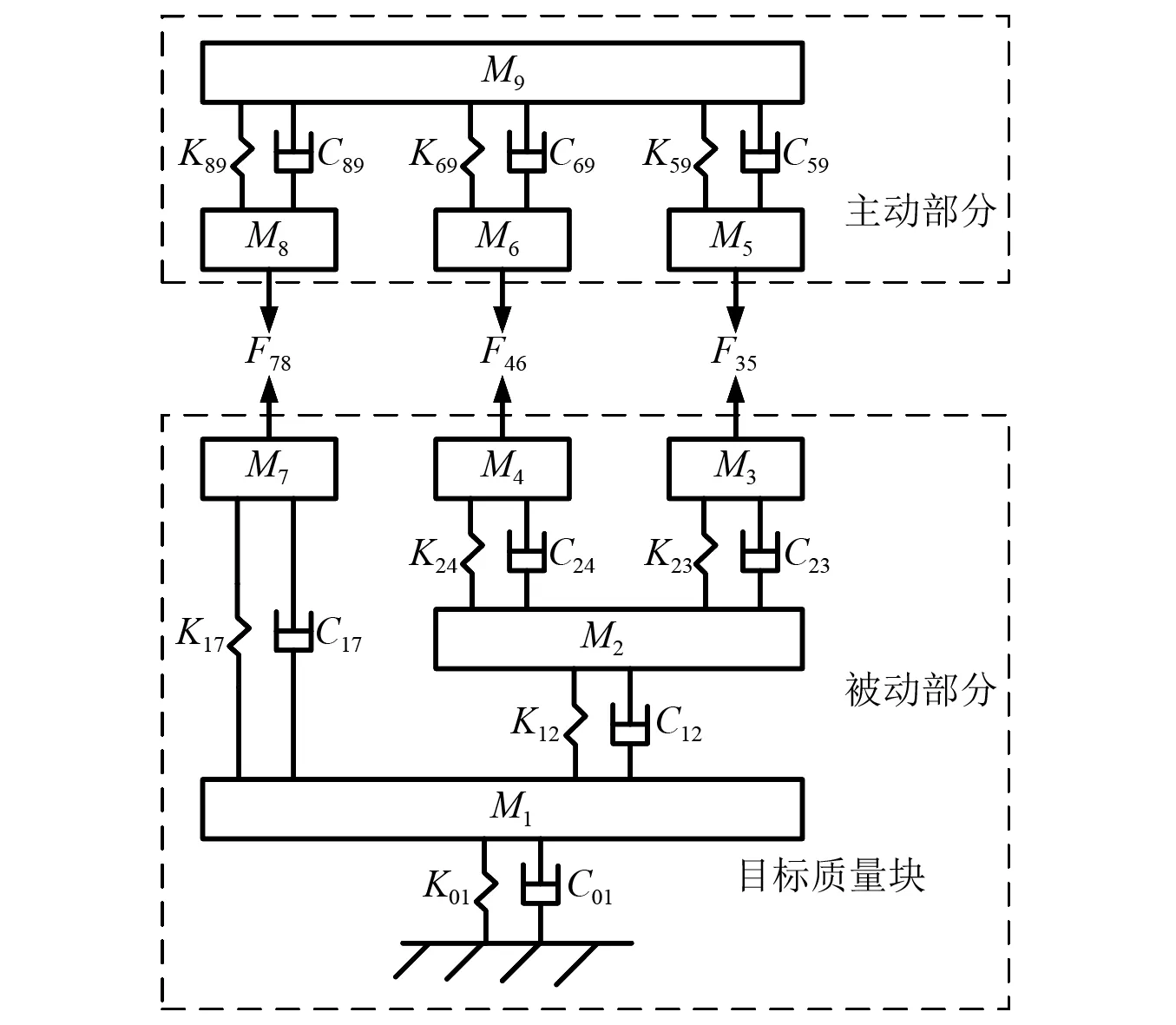
图3 拆分模型Fig.3 Split model

经典传递路径分析第二步是获取质量块M3，M4和M7受到的工况力(仅考虑工况一)。对于该九自由度模型，可采用悬置刚度法获取工况力

(14)

式中,(x3,x5,x4,x6,x7,x8)为工况一下的各质量块位移响应。

最后，通过工况力和对应的频响函数，即可得到工况一下各路径的贡献量(如图4～图7所示)。

(15)

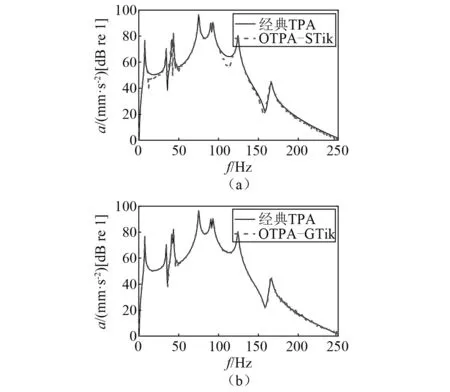
图4 目标点总响应Fig.4 The total response of the target point

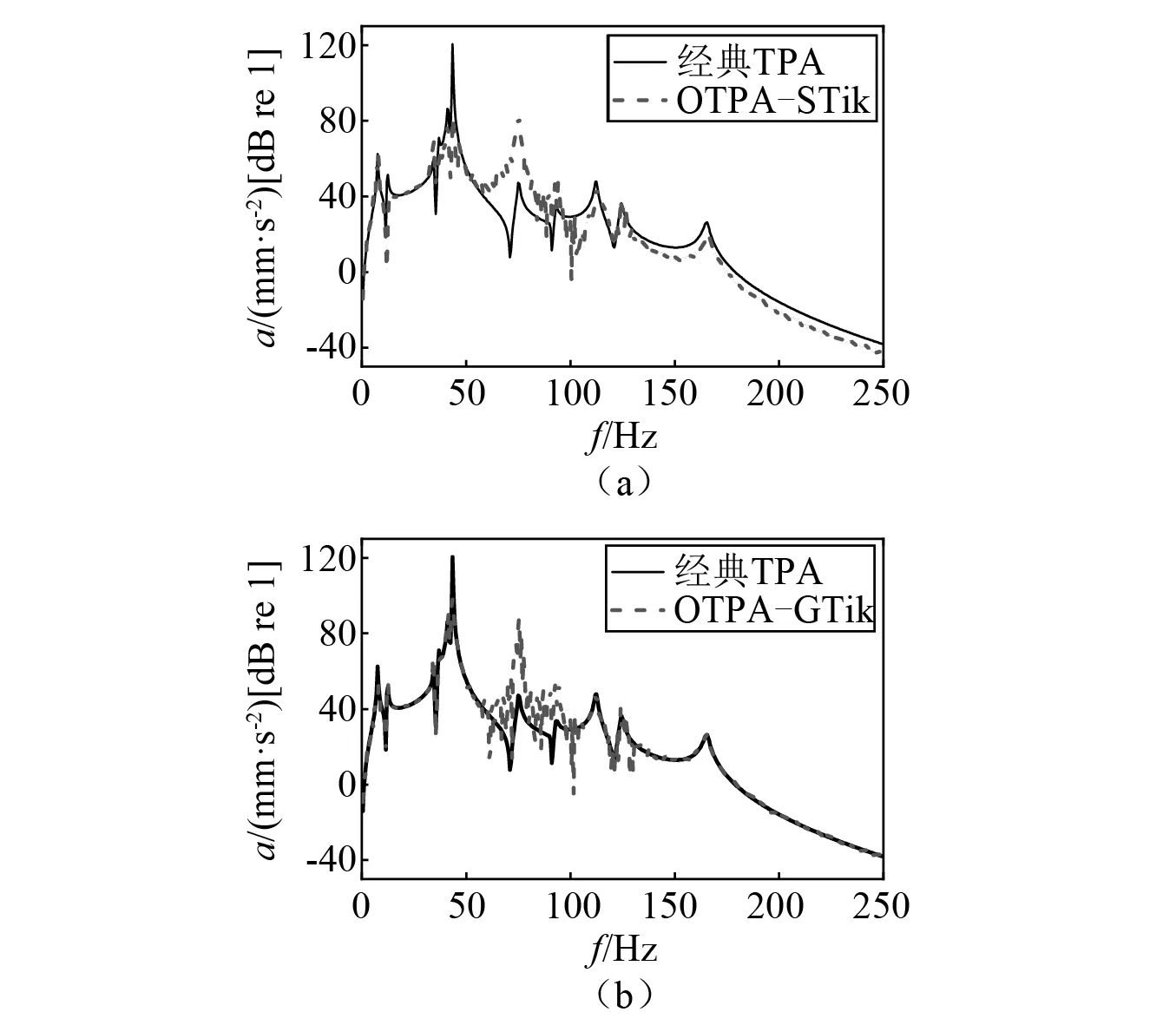
图5 路径35Fig.5 The contribution of path 35

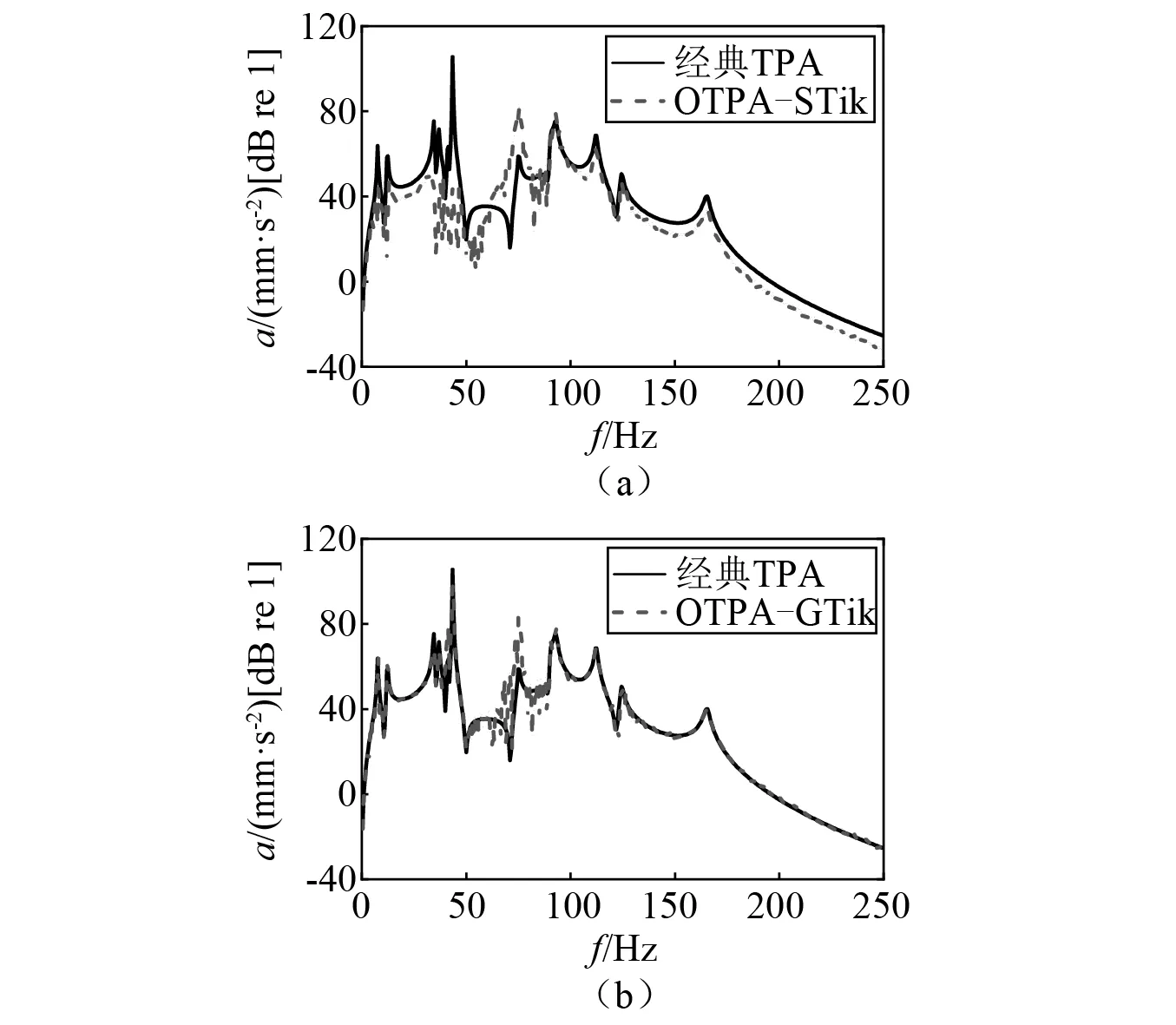
图6 路径46Fig.6 The contribution of path 46

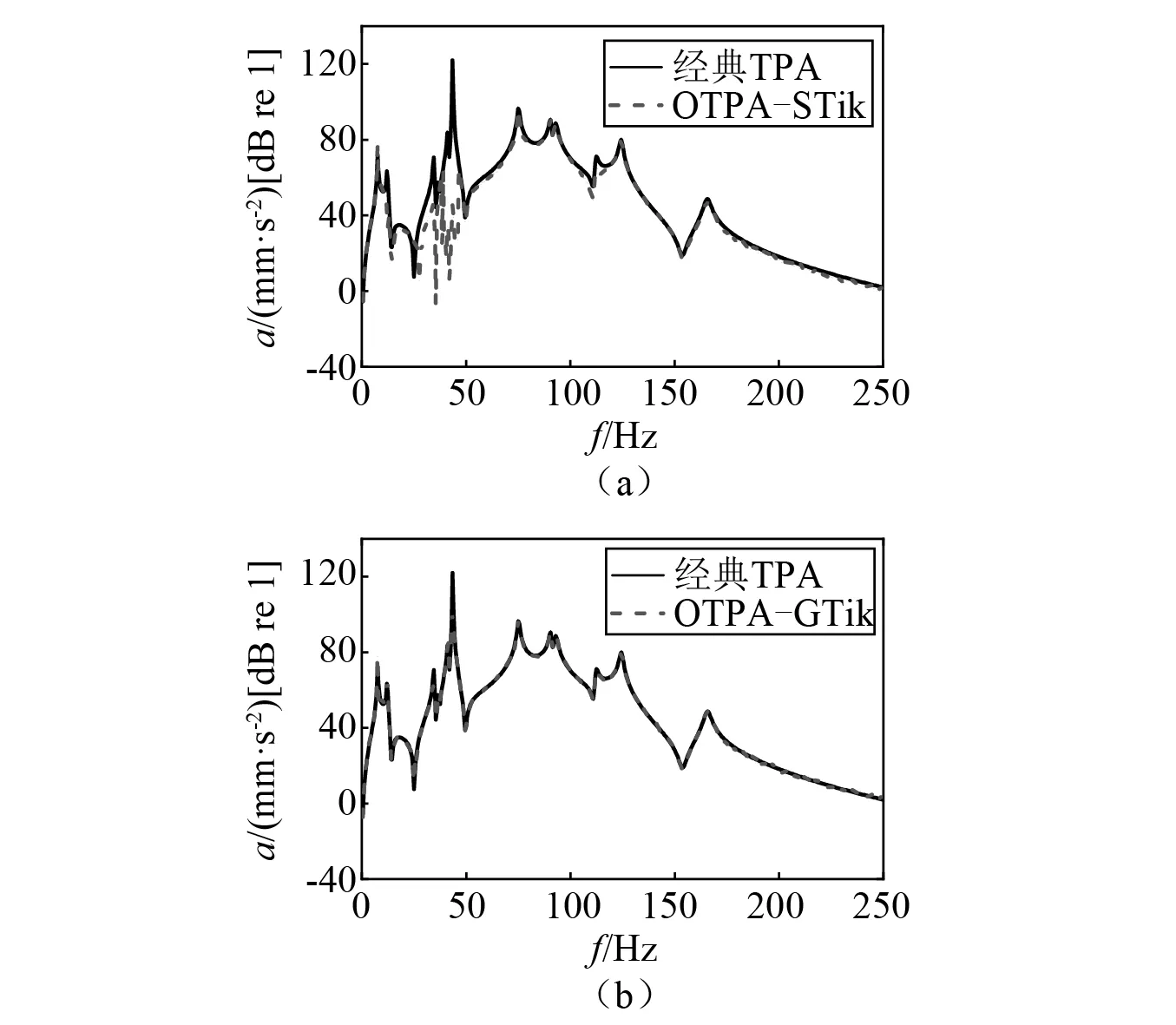
图7 路径78Fig.7 The contribution of path 78

2.2 工况传递路径分析

2.2.1 耦 合

在工况传递路径分析中，某个指示点的信号应仅为相应源的响应信号。然而，每种工况下，所有源同时工作，因此每个指示点的信号均耦合有其他源的信息。耦合会影响工况传递路径的贡献量辨识，若以含有耦合的信号进行工况传递路径分析，准确度较低。在存在耦合的情况下

(16)

为消除耦合的影响，可在主、被动部分上分别布置一个指示点，然后以两个指示点的响应差进行工况传递路径分析，即指示点响应矩阵取

X=[x3-x5x4-x6x7-x8]

2.2.2 工况传递路径分析

在实际测量过程中，测量数据不可避免会受到噪声的干扰，因此假设仿真所得的目标点响应矩阵Y和指示点响应矩阵X受随机噪声的影响，噪声服从高斯分布

(17)

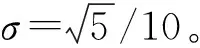
结合4组工况数据，分别运用标准Tikhonov正则化法与广义Tikhonov正则化法估计目标点与指示点之间的传递率函数矩阵。得到传递率矩阵后，根据式(5)计算工况一的各路径贡献量，并与2.1节的经典传递路径分析各路经贡献量进行对比，见图4～图7。

由图4可知，广义Tikhonov正则化法合成的工况传递路径分析总响应与经典传递路径分析总响应吻合很好，而标准Tikhonov正则化法合成的工况传递路径分析总响应在某些频段稍有偏差。对于路径35，在60～80 Hz处，两种工况传递路径方法得到的贡献量均有偏差，而在其他频率段，广义Tikhonov正则化法比标准Tikhonov正则化法准确度高。对于路径46和路径78，广义Tikhonov正则化法得到的贡献量在整个分析频率段与经典传递路径分析的贡献量吻合均较好，而标准Tikhonov正则化法在分析频段内误差较大。由此可知，当采用广义Tikhonov正则化法来估计传递率函数矩阵，最后获取的路径贡献量准确度更高，验证了广义Tikhonov正则化法在工况传递路径分析中的有效性。

为量化两种工况传递路径分析法获取的贡献量与CTPA结果的匹配程度，引入FRAC(frequency response assurance criteria)值CFRA[23]

(18)

式中：f1与f2为分析的频段上下限；YOTPA(f)为工况传递路径分析获得的贡献量；YTPA(f)为经典传递路径分析获得的贡献量；“*”为复共轭。FRAC值介于0～1，1为两个频域数据完全匹配。

图8是两种工况传递路径分析法的FRAC值。由图8可知，广义Tikhonov正则化法的FRAC值均大于标准Tikhonov正则化法的FRAC值，也表明广义Tikhonov正则化法获取的路径贡献量准确度更高。

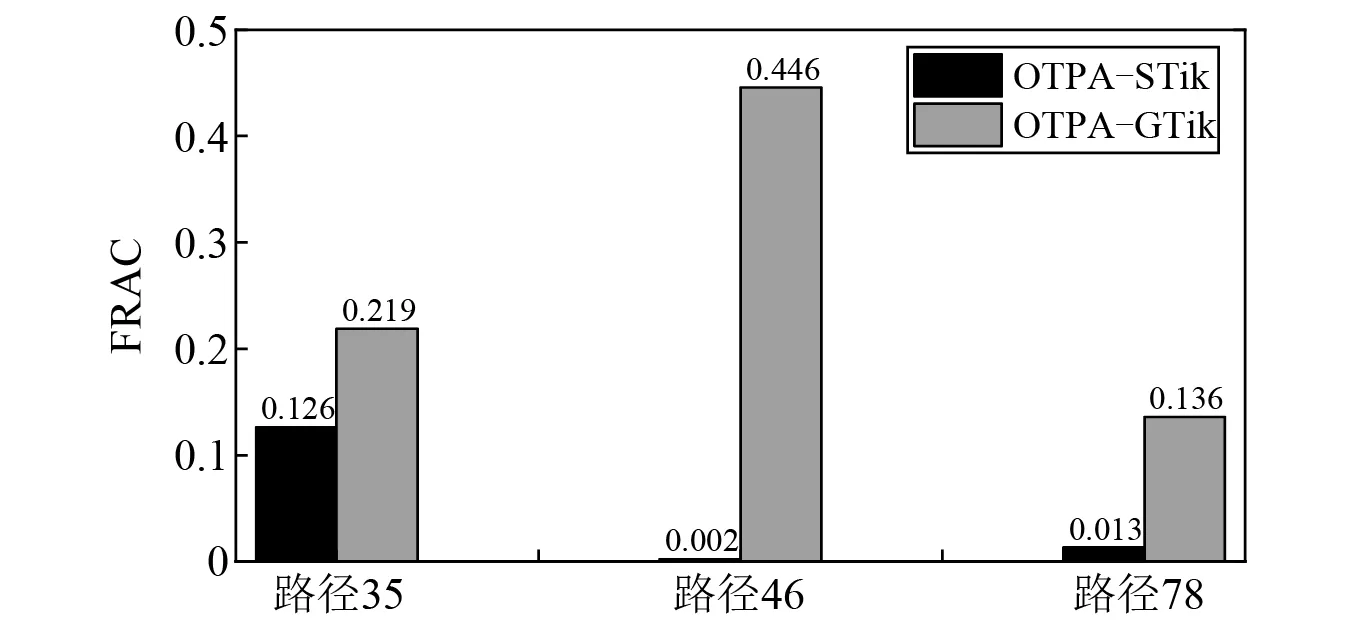
图8 仿真FRAC值Fig.8 The FRAC value of simulation

3 实验验证

为了进一步对比标准Tikhonov正则化法和广义Tikhonov正则化法在工况传递路径分析中的效果，在一铝板上进行工况传递路径分析实验，如图9所示。铝板一端固定在支架上。铝板长×宽×厚为800 mm×400 mm×5 mm，密度为2 700 kg/m3，泊松比为0.31，弹性模量为71 000 MPa。

图9 实验布置图Fig.9 The setup for experiment

激励源为两个激振器，记为源a和源b。通过改变激励类型，产生4组垂直于板面的激励力(即4组工况，如表2所示)，并分别用两个力传感器记录激励力的大小。对每个激励源布置一个指示点(指示点1和指示点2)，指示点应尽量靠近激励源；选择点Y为目标点，用加速度计测试指示点与目标点垂直于板面的振动加速度。

表2 实验工况Tab.2 The experimental operations

3.1 经典传递路径分析

仍以经典传递路径分析获取的贡献量为准确值，因此首先进行经典传递路径分析。经典传递路径分析第一步测试源a和源b到目标点Y的频率响应函数Hya和Hyb。第二步，以力传感器的输出值为工况力，即直接测量法获取激励源的工况力。频响函数Hya和Hyb如图10所示。源a和源b的工况力(工况一)如图11所示。

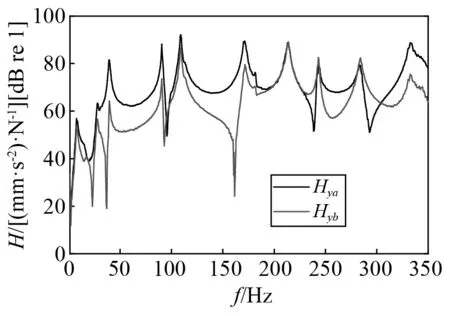
图10 频响函数Hya和HybFig.10 FRF Hya and Hyb

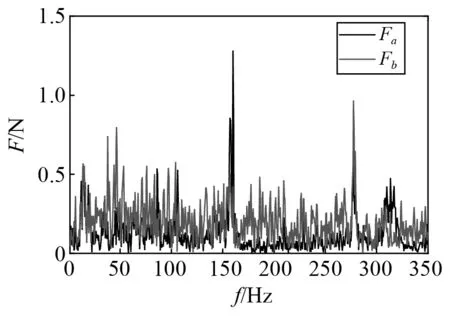
图11 工况力Fa和FbFig.11 The operational load Fa and Fb

最后通过已获取的频率响应函数和工况力，即可得到两条路径的贡献量。两条路径贡献量的总和即为目标点的总响应，并与实际所测目标点响应对比验证经典传递路径分析的正确性，如图12所示。由图12可知，在整个分析频段内，合成的总响应与目标点实测响应吻合较好，表明经典传递路径分析结果可信。

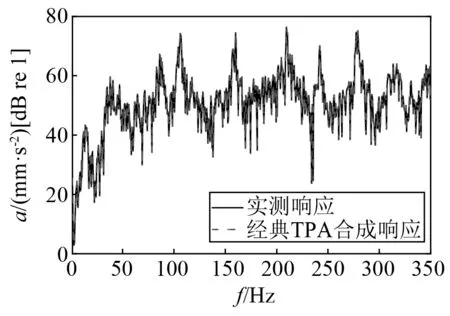
图12 目标点Y的实测响应与CTPA合成响应Fig.12 The measured response and synthesized response of target point Y

3.2 工况传递路径分析

3.2.1 耦 合

与仿真一致，指示点信号若耦合有其他源的信息，如图13所示。耦合同样会影响实验工况传递路径结果的准确度。因此在进行工况传递路径分析之前，需要消除耦合的影响。

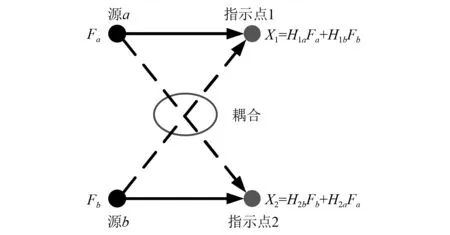
图13 耦合示意图Fig.13 The sketch for crosstalk

对于指示点1，其实测响应X1可表示为

X1=H1aFa+H1bFb

(19)

式中:Fa和Fb分别为源a和源b的载荷；H1a和H1b分别为源a和源b到指示点1的频率响应函数；H1bFb即为X1含有的耦合;Fb通过力传感器可测得，因此只需测试获得频响函数H1b，即可消除X1的耦合部分

(20)

对于指示点2，可采用同样的方式消除耦合部分。指示点1和指示点2的响应(工况一)消除耦合前后对比，如图14所示。由图14可知，指示点信号消除耦合前后，在某些频段变化较大。因此，若以未消除耦合的信号进行后续工况传递路径分析，势必降低工况传递路径分析结果的可信度，也说明消除耦合的重要性。

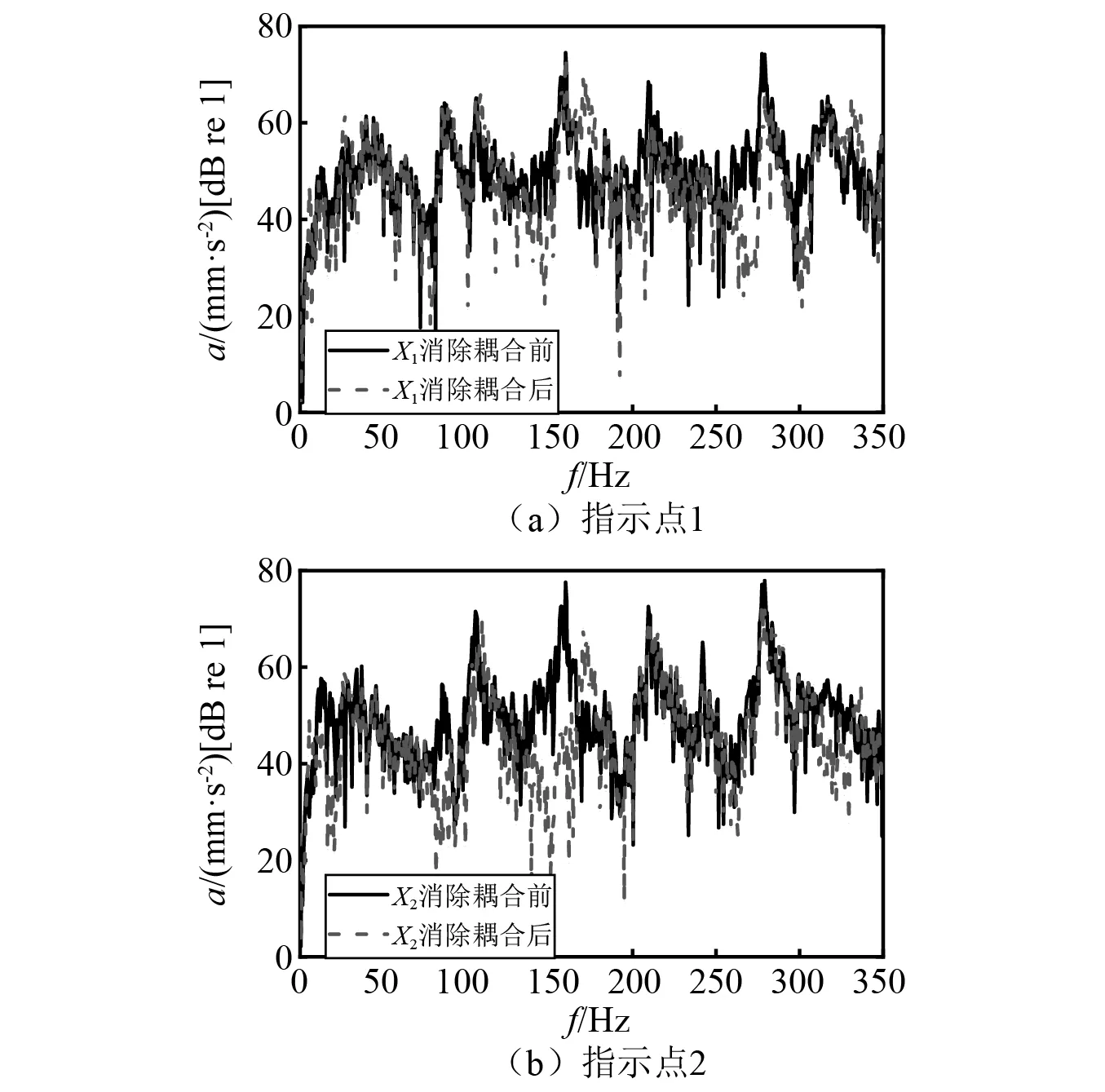
图14 消除耦合前后对比Fig.14 Comparison before and after eliminating coupling

3.2.2 工况传递路径分析

根据式(20)消除4组工况数据中指示点1和指示点2的耦合部分后，然后分别利用标准Tikhonov正则化法和广义Tikhonov正则化法估计目标点与指示点之间的传递率函数矩阵，最后根据式(5)得到每条路径的贡献量。图15是两种工况传递路径分析方法合成的目标点总响应曲线图。图16与图17分别是路径1与路径2的贡献量图。

图15 目标点总响应Fig.15 The total response of target point

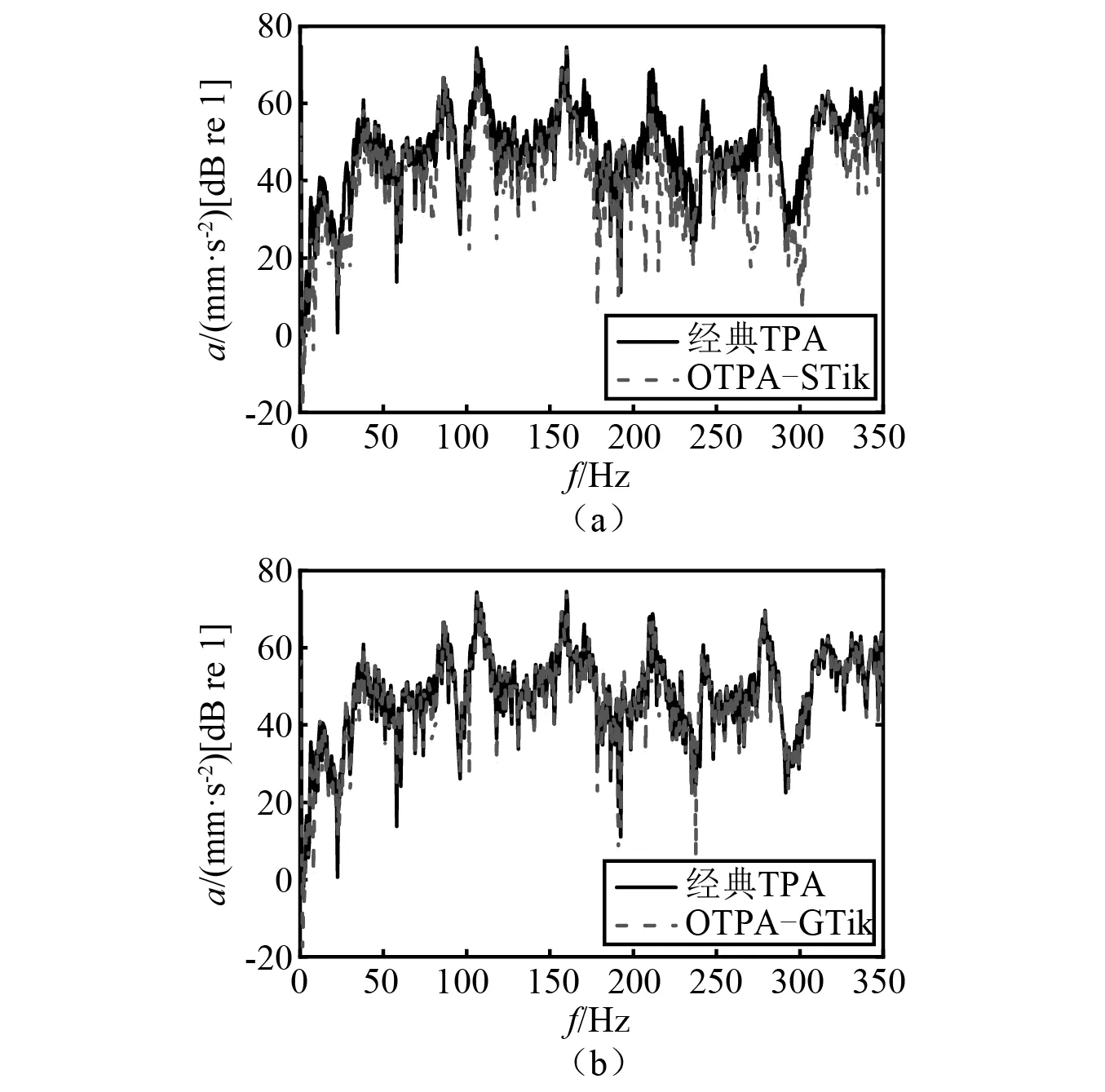
图16 路径1贡献量Fig.16 The contribution of path 1

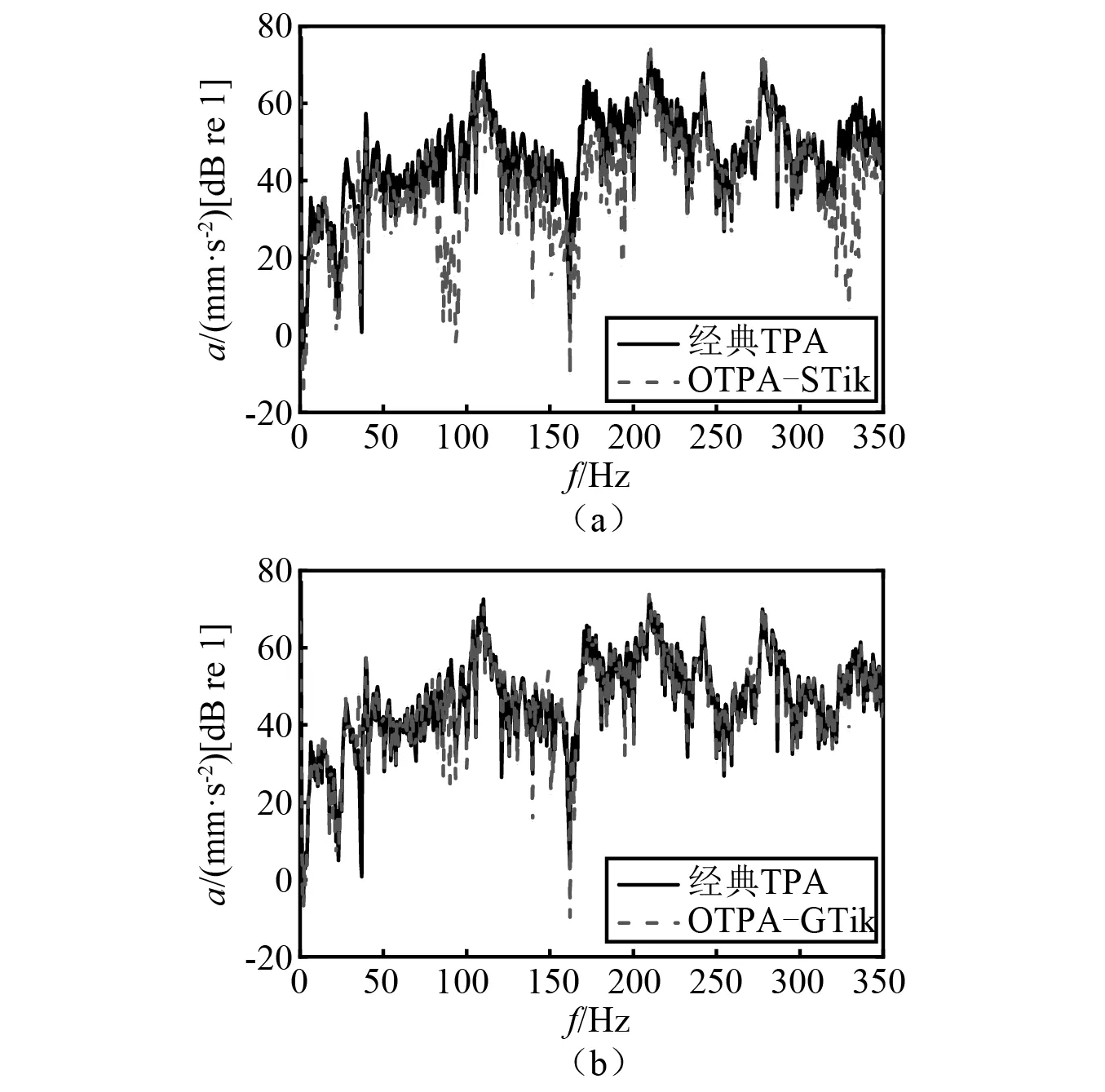
图17 路径2贡献量Fig.17 The contribution of path 2

图15中，广义Tikhonov正则化工况传递路径分析法合成的总响应与CTPA结果吻合较好，误差较小。而标准Tikhonov正则化工况传递路径分析法合成的总响应与CTPA结果有些许偏差，表明标准Tikhonov正则化法在估计传递率函数矩阵时，出现了较大的误差。

从图16与图17每条路径贡献量结果可知，广义Tikhonov正则化工况传递路径分析法获得的每条路径贡献量与CTPA结果在整个分析频段内吻合较好，只在某些频率有偏差，表明广义Tikhonov正则化法获得的传递率矩阵准确度较高，识别贡献量效果较好。而标准Tikhonov正则化工况传递路径分析法获得的每条路径贡献量在整个分析频段内失真较严重，识别贡献量的准确度较低。

同样采用FRAC值来对比两种工况传递路径分析法获取的贡献量与CTPA结果的匹配程度。图18是两种工况传递路径分析法的FRAC值。由图18可知，广义Tikhonov正则化工况传递路径分析法的FRAC值为0.858和0.799，大于标准Tikhonov正则化工况传递路径分析法的FRAC值：0.741和0.635，表明广义Tikhonov正则化工况传递路径分析的各路径贡献量与CTPA结果匹配更好，也说明广义Tikhonov正则化法用于工况传递路径分析中，能获得准确度更高的贡献量，能更准确地识别振动传递的主导路径。

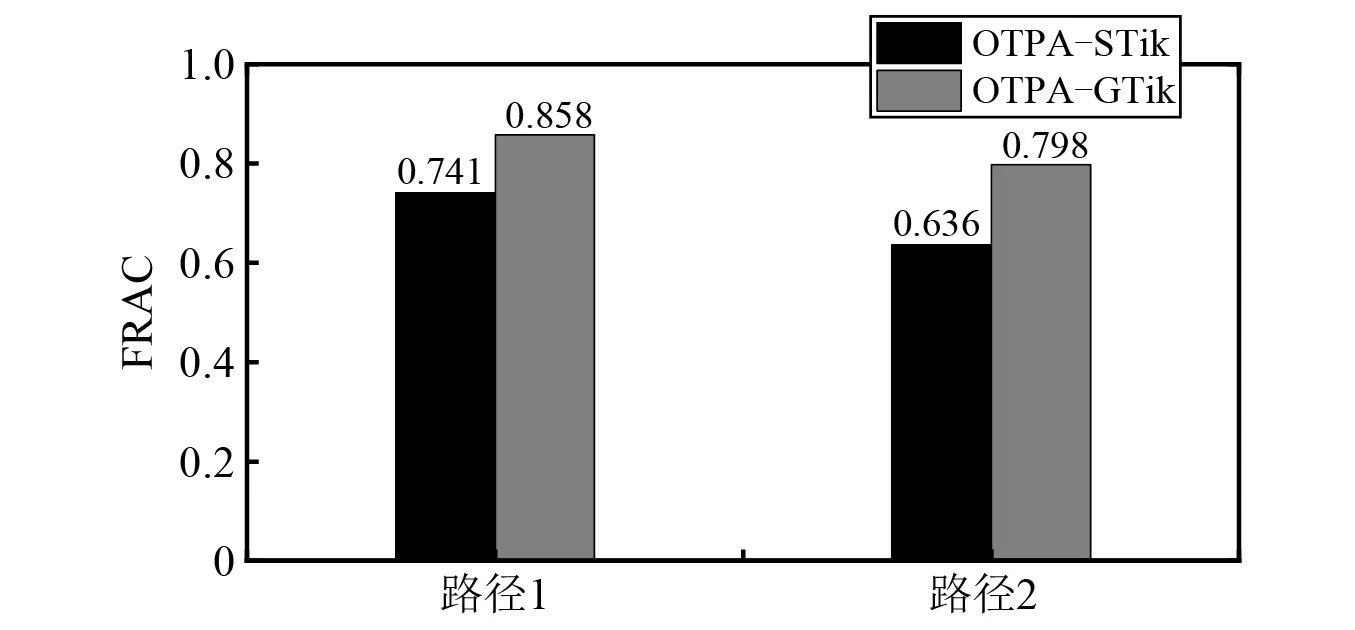
图18 FRAC值Fig.18 The FRAC value

4 结 论

将以一阶偏导矩阵作为正则化矩阵的广义Tikhonov正则化应用于工况传递路径分析中，利用广义奇异值分解得到正则化解的基向量和L曲线法选取正则化参数，得到了广义Tikhonov正则化工况传递路径分析的各路径贡献量。最后通过工况传递路径分析仿真与实验发现，与标准Tikhonov正则化相比，广义Tikhonov正则化在识别路径贡献量方面准确度更高。