基于矩的传递函数模型的“不兼容”非高斯风压过程模拟研究

吴凤波， 姜 言， 彭留留， 吴 波， 罗 颖

(1. 重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；2. 西南大学 工程技术学院，重庆 400700； 3. 重庆大学 土木工程学院，重庆 400044；4. 长沙理工大学 土木工程学院，长沙 410015)

风压通常被用于建筑结构抗风设计，特别是建筑围护结构的抗风设计。研究表明，建筑迎风区域的风压可以用高斯分布进行描述，而分离区处的风压常常具有显著的非高斯特性[1-3]。结构风致响应非线性分析通常需要较长风压时程，因此准确模拟非高斯风压对于建筑结构的抗风设计十分重要。

由于简便性，传递过程法被广泛用于非高斯风压的模拟[4-7]。传递过程法的思想是将非高斯过程表示为高斯过程的函数，该函数通常被称为传递函数。Winterstein[8]研究表明，非高斯过程可显式地表示为对应高斯过程的Hermite多项式，因而Hermite多项式模型(Hermite polynomial model,HPM)被广泛用于非高斯风压的模拟[9]和极值估计[10]。由于传递函数具有单调性的要求，HPM具有一定范围的可行区。这就意味着，对于不在HPM可行区内的非高斯风压，HPM不再适用。最近，Johnson转换模(Johnson transformation model,JTM)[11]由于具有比HPM更大的可行区而被用作传递函数。Wu等[12]围绕HPM和JTM在非高斯风压模拟方面进行了系统的对比研究，研究表明HPM和JTM对弱非高斯风压的模拟效果较好，而对强非高斯风压的模拟效果不佳。HPM和JTM的模型参数通常可基于非高斯过程前4阶统计矩(均值、标准差、偏度、峰度)进行估计，因而又被称为基于矩的传递函数模型。

首先，本文介绍了HPM和JTM两个模型；其次，给出了两个模型模拟“不兼容”非高斯风压的方法；随后从理论上对比了两个模型模拟非高斯风压时出现不兼容情况的异同；最后，基于数值案例对两种模型模拟“不兼容”非高斯风压的效果进行了系统的对比和评估。

1 基于矩的传递函数模型

1.1 HPM模型

当标准非高斯过程Y(t)的峰度大于3时，Y(t)可表示为相应标准高斯过程Z(t)的Hermite多项式函数

(1)

式中，κ，h3和h4为模型系数，可根据Y(t)的偏度和峰度进行估计，估计公式见文献[13]。

当Y(t)的峰度小于3时，它可表示为[14]

(2)

式中，a′=b3/(3b4)；c′=(b′-a′2)3；b′=(b2-b3α3-b4α4)/(3b4)，b2,b3,b4为模型系数，可根据Y(t)的偏度和峰度进行估计，其估计公式见Ding等的研究，其中α3和α4分别为偏度和峰度。

由于传递函数需要满足单调性的要求，因此HPM具有一定的可行区，如图1所示。对于软化过程，HPM可行区可表示为

3+(1.25α3)2≤α4

(3)

对于硬化过程，HPM可行区可表示为

1.25+(1.35α3)2≤α4

(4)

1.2 JTM模型

Johnson基于中心极限定理提出一种能够将标准高斯过程Z(t)转换为标准非高斯过程Y(t)的四参数转换模型，该模型被称为Johnson转化模型(JTM)。一般地，JTM可表示为

(1) 无界转换模型，SU

y=g(z)=ε+λsinh[(z-γ)/η]

(5)

(2) 有界转换模型，SB

y=g(z)=ε+λ{1+exp[(γ-z)/η]}-1

(6)

(3) 对数正态转换模型，SL

y=g(z)=ε+λexp[(z-γ)/η]

(7)

式中：ε和γ为控制Johnson曲线位置的参数；λ和η为控制JTM曲线尺度的参数，其值总是大于零。这4个参数可基于标准非高斯过程Y(t)的偏度和峰度经迭代计算获得，具体详情可见Wu等的研究。

SL转换的可行区是偏度-峰度图中的一条曲线，该曲线的闭合表达式为

(8)

α4=w4+2w3+3w2-3

(9)

式中，w=exp(η-2)。

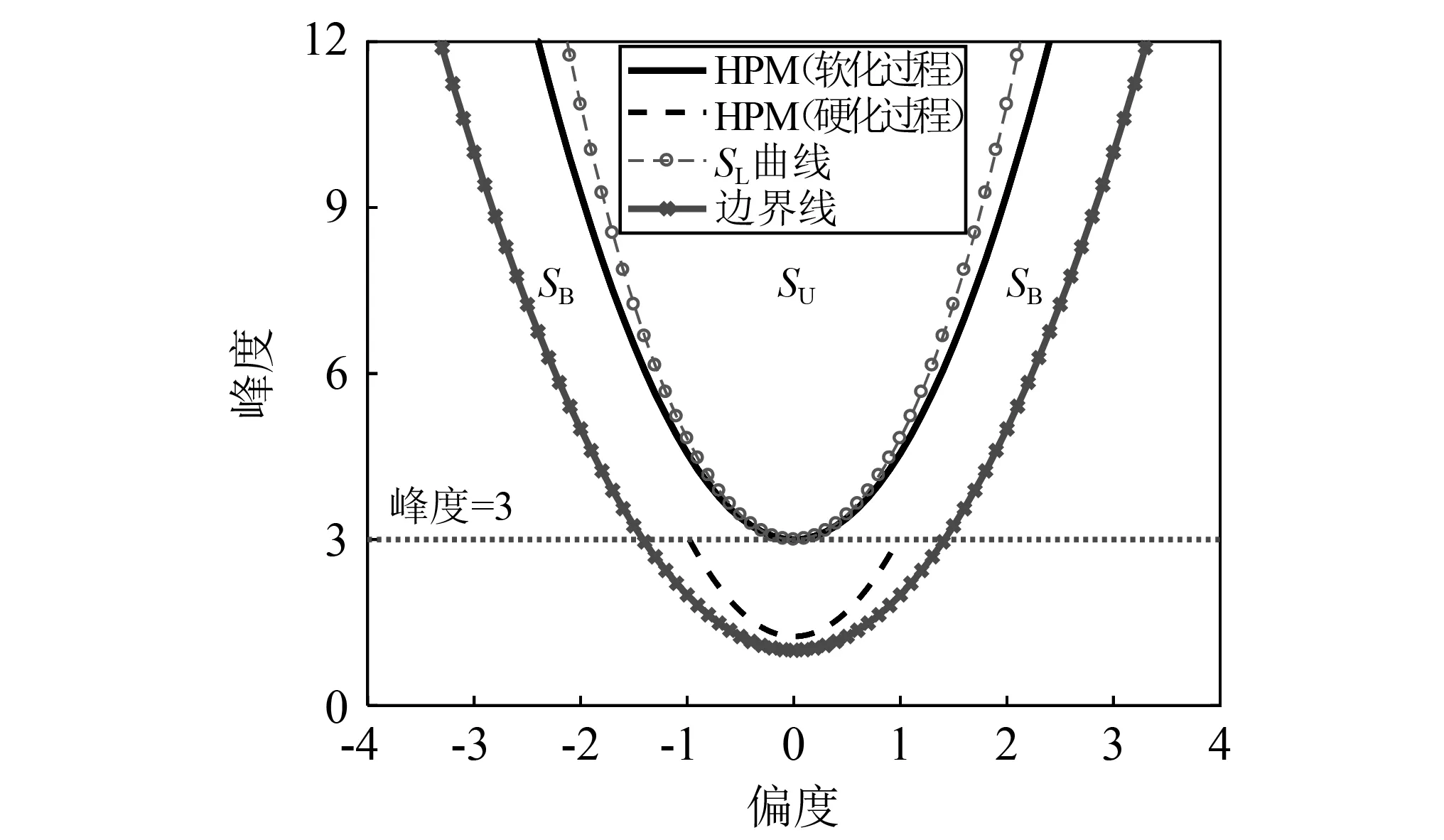
图1 HPM和JTM模型的适用范围Fig.1 Application range of HPM and JTM models

2 “不兼容”非高斯风压过程的模拟

2.1 基于谱的高斯风压模拟方法

本文主要运用谱表示法进行高斯随机过程的模拟。谱表示法是一种利用谱分解和三角函数技术叠加来模拟随机过程样本的方法。以一维单变量零均值平稳高斯随机过程为例，该方法可表示为[15]

(10)

Al=[2SZ(ωl)Δω]1/2,l=0,1,…,N-1

(11)

ωl=lΔω,l=0,1,2,…,N-1

(12)

Δω=ωu/N

(13)

2.2 相关函数偏离关系

在模拟得到高斯过程样本后，将这些样本通过传递函数HPM或JTM即可得到相应的非高斯过程样本。但模拟前我们往往只知道非高斯过程的功率谱或相关函数，且高斯过程相关函数与非高斯过程相关函数存在偏差。因此，我们需要先基于非高斯过程Y(t)的功率谱或相关函数得到相应高斯过程的功率谱或相关函数。

Grigoriu给出了标准非高斯过程Y(t)的自相关函数ρNG(τ)为

(14)

式中，z1=z(t)，z2=z(t+τ)，φ[z1,z2;ρG(τ)]为二元标准高斯向量的联合概率密度函数，其表达式为

(15)

式(14)通常被称为相关函数偏离关系，已知ρNG(τ)，通常情况下可通过迭代法(如牛顿迭代法)求解相关函数偏离关系来获得ρG(τ)。然而，当由JTM或HPM表示的概率分布与指定的标准非高斯过程功率谱SY(ω)“不兼容”时，式(14)的解不存在。下面就“不兼容”情况展开详细说明。

2.3 “不兼容”非高斯过程的模拟方法

对于上述两种不兼容情况，国内外学者基于传递过程理论，提出了几种获得与非高斯过程概率分布兼容的功率谱的迭代方法。在这些方法中，Shields等[16]针对单变量模拟提出的迭代方法不仅精度高，而且计算效率高。因此，本文也采用该方法来评估HPM和JTM模拟“不兼容”非高斯风压的性能。该迭代方法可表示为

(16)

(17)

当迭代所产生的误差变化很小时，迭代结束。

2.4 “不兼容”非高斯过程的模拟流程

假定非高斯过程X(t)的前4阶矩分别为μX，σX，α3X和α4X，X(t)的相关函数记为RX(τ)。基于HPM或JTM模拟非高斯过程X(t)的步骤如下。

步骤1标准化X(t)以获得标准非高斯过程Y(t)，则μY=0；σX=1;α3Y=α3X;α4Y=α4X；ρNG(τ)=RY(τ)=

步骤2基于标准非高斯过程Y(t)的前4阶矩估计HPM和JTM模型参数，得到HPM和JTM传递函数。

步骤3采用傅里叶变换将ρNG(τ)转化为功率谱，即获得目标功率谱SNG,Tg(ω)。

步骤4按照2.3节确定由HPM或JTM表示的非高斯过程概率分布与目标非高斯过程功率谱是否存在不兼容。当出现不兼容，按照以下步骤继续模拟。

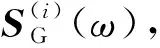
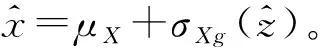
3 HPM和JTM的理论对比

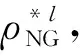
图2 HPM和JTM确定的非高斯过程相关函数最小值(软化过程)Fig.2 The minimum values of the non-Gaussian correlation functions by HPM and JTM (softening process)

图3 HPM和JTM确定的非高斯过程相关函数最小值(硬化过程)Fig.3 The minimum values of the non-Gaussian correlation functions by HPM and JTM (hardening process)

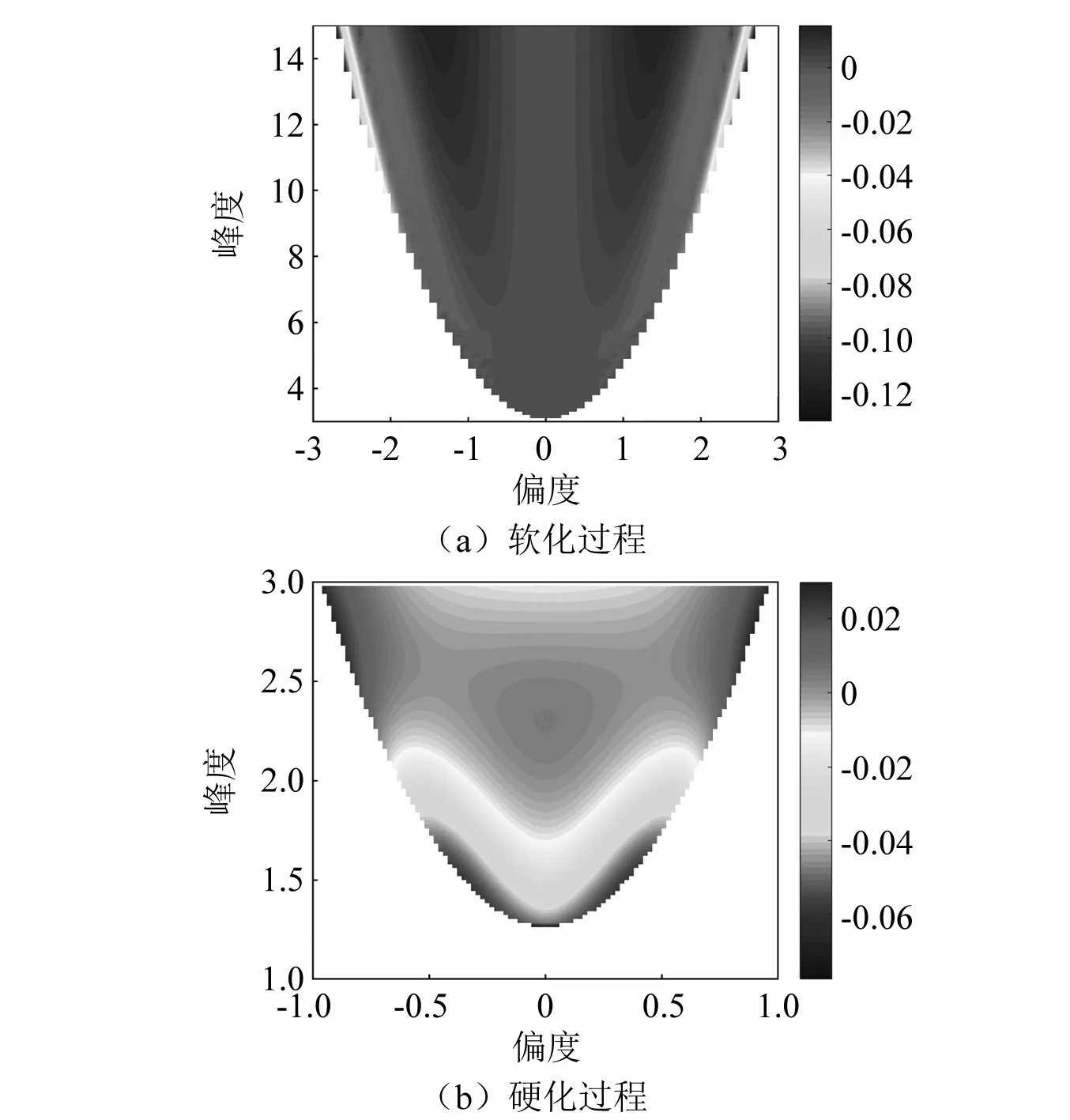
图4 HPM与JTM确定的非高斯过程相关函数最小值间的相对差距Fig.4 The relative gap between the minimum value of the non-Gaussian correlation functions by HPM and JTM

其次，我们对比HPM和JTM出现第二类不兼容的情况。同第一类不兼容情况一样，为了获得较为全面的结论，我们针对软化和硬化过程开展对比研究。同时，图2和图3表明基于式(14)获得的相关函数对峰度不太敏感，而对偏度较为敏感，因此这里重点探讨指定峰度下相关函数随偏度变化而如何变化的问题。

参考Grigoriu，本文取标准非高斯过程相关函数如下

(18)

对于标准软化过程，给定非高斯过程相关函数，基于HPM或JTM采用式(14)经迭代计算获得指定峰度为22偏度分别为-0.5和-3.0的高斯过程相关函数ρG(τ)；对于标准硬化过程，按照类似方法获得指定峰度为2.5偏度分别为-0.3和-0.7的高斯相关函数ρG(τ)。获得ρG(τ)后，采用傅里叶变换即可获得高斯过程功率谱SG(ω)，如图5所示。从图5可知，偏度(绝对值)越大，基于HPM和JTM获得的高斯过程功率谱最小值越小，即更易出现第二类不兼容情况。此外，基于HPM获得的高斯过程功率谱最小值小于基于JTM获得的相应值，即HPM比JTM更易出现第二类不兼容情况。

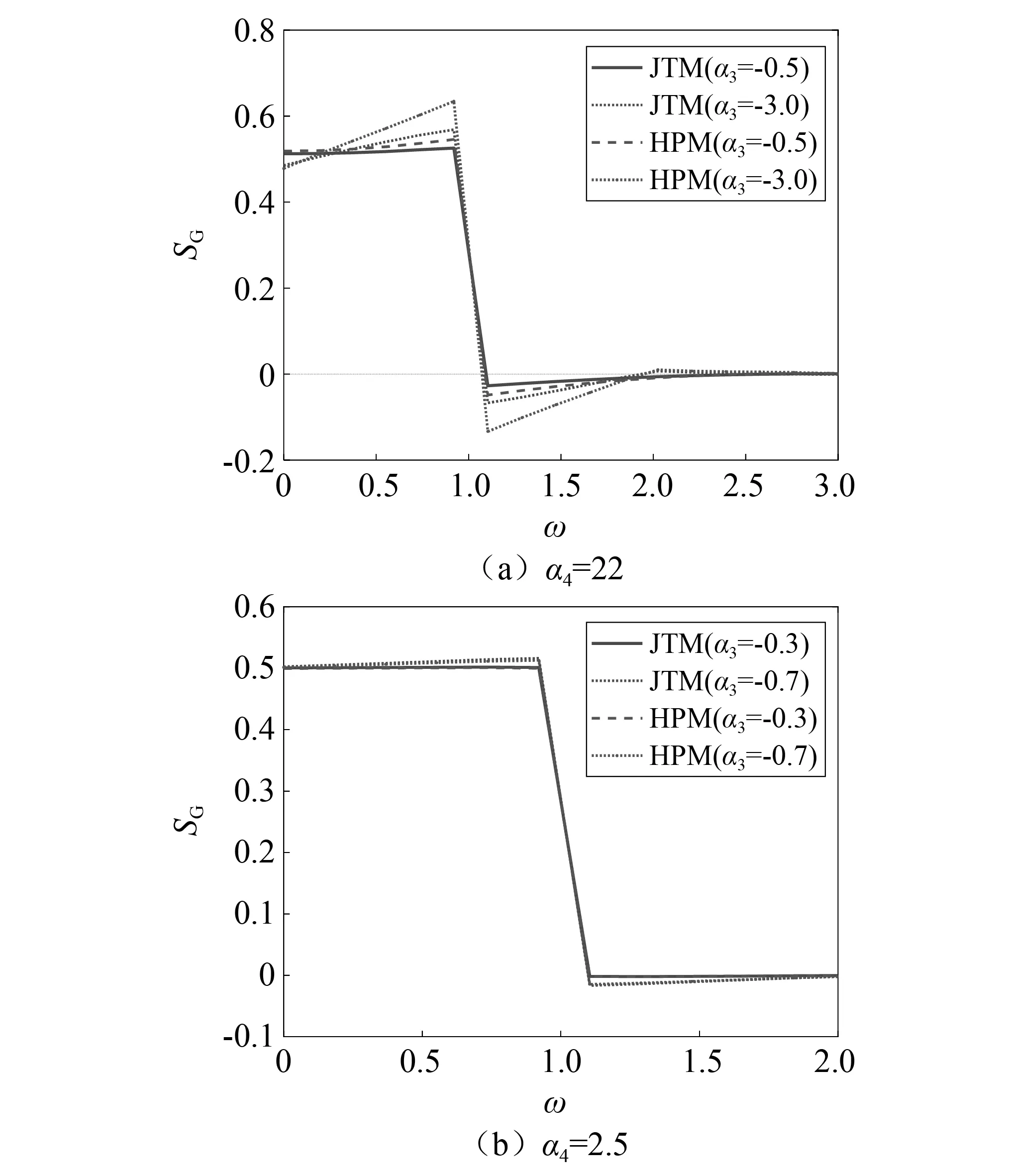
图5 HPM和JTM确定的高斯过程功率谱Fig.5 PSDs of the Gaussian process by HPM and JTM

4 数值案例

(19)

式中：φ和Φ分别为标准高斯分布的概率密度函数和累计分布函数；ξ，δ和α分别为SG分布的位置、尺度和偏度参数。

SHS概率密度函数可表示为

p(x)=

(20)

式中,ξ，δ和α分别为SHS分布的位置、尺度和偏度参数。

本文将对3个偏度逐渐增大的非高斯过程进行数值模拟，重点探讨不同偏度对兼容性的影响，概率分布的参数信息，如表1所示。表1还列出了各分布的前4阶矩，以便用于确定HPM和JTM模型参数。

参考Grigoriu的研究，本文取标准非高斯过程的相关函数如下

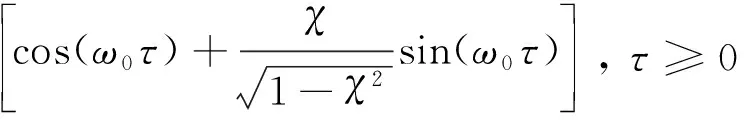
(21)

式中，ω0>0， 0<χ<1。通过逆傅里叶变换可将ρNG转化为目标功率谱SNG,Tg。

本文考虑两种相关函数，分别为窄带过程(χ=0.02;ω0=1.0)和宽带过程(χ=0.3;ω0=1.0)，见表1。将窄带过程和宽带过程对应的χ和ω0代入式(21)，可计算出目标相关函数ρNG(τ)的最小值分别为-0.94和-0.39。

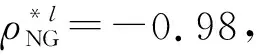
表1 数值模拟案例参数取值Tab.1 Theparameter values of the numerical simulation cases

图7对比了基于HPM和JTM迭代后获得兼容的非高斯过程功率谱SNG和目标功率谱SNG,Tg，其中误差ε定义见式(17)。从图7可知，基于JTM迭代产生的误差ε整体比基于HPM迭代产生的误差ε小一些。特别对于图7(d)中的强宽带非高斯过程，基于JTM获得的非高斯功率谱比基于HPM获得的功率谱更接近目标功率谱。

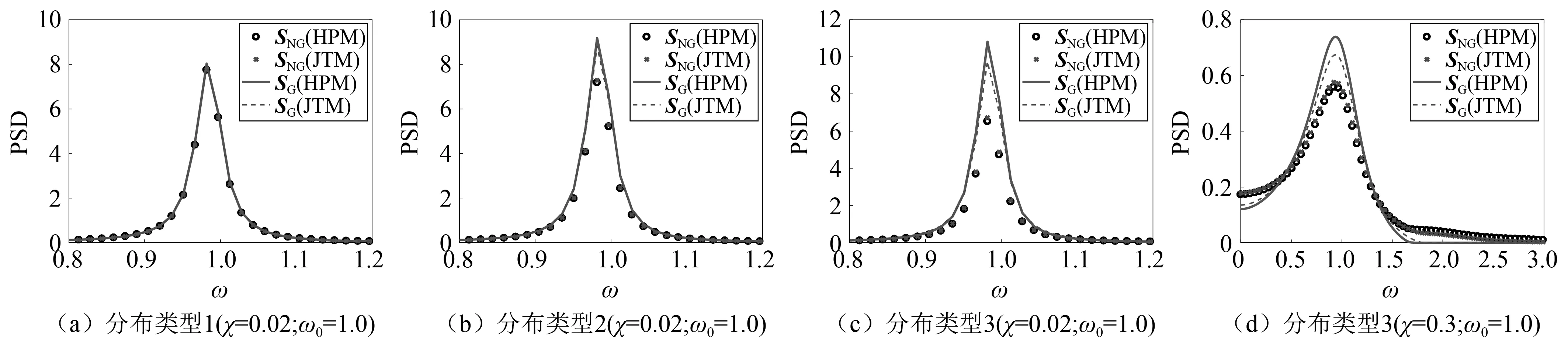
图6 基于传递函数模型迭代估计的高斯和非高斯过程的功率谱Fig.6 PSDs of the Gaussian and non-Gaussian processes by translation function models

基于迭代获得的最终高斯功率谱SG进行数值模拟。模拟中，取N=2 048，模拟样本为100。对比了模拟的非高斯概率密度(所有样本的均值)和目标概率密度，如图8所示。由图8可知，基于JTM和HPM模拟的概率密度整体上与目标值吻合较好，其中图8(c)～图8(d)表明基于JTM获得的非高斯概率密度比基于HPM获得的概率密度更接近目标值。

图7 基于转换函数模型迭代估计的非高斯过程的功率谱Fig.7 PSDs of the non-Gaussian process by translation function models

图8 基于转换函数模型模拟的非高斯过程概率密度函数Fig.8 PDFs of the non-Gaussian process by translation function models

5 结 论

本文首先对HPM和JTM两种传递函数模型进行了介绍；其次，介绍了“不兼容”非高斯风压过程的模拟方法；然后，基于理论分析，针对软化过程和硬化过程系统对比了HPM和JTM两种模型出现第一类和第二类不兼容的情况；最后基于具体数值案例对HPM和JTM模拟“不兼容”非高斯过程做了系统评估。整个研究得出以下结论：

(1) 理论分析表明，基于HPM和JTM获得的非高斯相关函数最小值对峰度值不太敏感，而对偏度较为敏感。随着偏度值(绝对值)增加，基于HPM和JTM获得的非高斯相关函数和高斯功率谱最小值增加，即HPM和JTM更易出现第一类不兼容；同时，基于HPM和JTM获得的高斯过程功率谱最小值越小，即HPM和JTM更易出现第二类不兼容。

(2) 理论分析表明，对于软化过程，在偏度-峰度坐标系中的左上方或右上方局部区域里，JTM通常比HPM更易出现第一类不兼容情况；在靠近偏度-峰度坐标系中可行区边缘区域，HPM通常比JTM更易出现第一类不兼容情况。对于峰度大于2.2的强偏斜硬化过程，JTM通常比HPM更易出现第一类不兼容情况；而对于峰度小于2.2的强偏斜硬化过程，HPM通常比JTM更易出现第一类不兼容情况。

(3) 数值案例表明，相比HPM，基于JTM迭代获得的非高斯功率谱更接近目标值，即JTM模拟“不兼容”非高斯风压过程的总体效果比HPM稍好。

致谢

感谢国家自然科学基金(51908074)、重庆市自然科学基金面上项目(cstc2021jcyj-msxmX1141；CSTB2022NSCQ-MSX1349)和重庆市教育委员会科学技术研究项目(KJQN202200729)对本文的资助。