大高宽比浮放馆藏文物运动状态影响因素研究

杨维国， 葛家琪， 张家铭， 王 萌， 刘 佩， 邹晓光

(1. 北京交通大学 土木建筑工程学院，北京 100044; 2. 中国航空规划设计研究总院有限公司，北京 100120)

馆藏文物是我国文化的瑰宝，馆藏文物大多采用浮放的方式陈列，在地震来临时容易产生滑移、摇摆甚至倾覆等不同的运动状态[1-2]。由于传统的抗震设计方法和减隔震设计方法均是以保护建筑结构主体为目的提出的，对于浮放文物这类非结构构件没有进行充分地考虑[3]。在地震来临时，即便博物馆主体结构没有损坏，也不能保证馆藏浮放文物的安全，因此对浮放文物运动状态的研究是相当必要的[4]。

由于浮放文物在地震作用下的响应是高度的非线性行为，可供参考的试验数据较少，理论公式多是以简谐波或脉冲形式提出的[5-8]，对复杂的地震作用下的运动状态的研究还比较稀缺。目前国内外对浮放运动状态的研究[9-12]多是基于Housner[13]提出的SRM (simple rocking model)，该模型将浮放文物简化为平面内的矩形刚体，并严格绕两个底端角点发生转动，然后通过小角度内的线性近似得到文物的摇摆运动方程。但实际上文物体态各异，实际发生的运动状态也并非完全符合这些假定。因此，对浮放系统运动状态的影响因素及其影响机理的研究可以在一定程度上为馆藏文物的防震工作提供理论指导的依据。

基于上述原因，对浮放文物运动状态及其影响因素和安全控制指标的研究具有重要意义。

1 浮放馆藏文物摇摆系统理论

1.1 摇摆运动理论

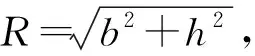
(1)

式中，sgn(θ)为关于θ的符号函数

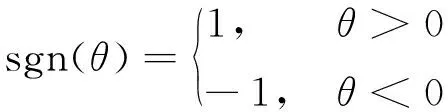
(2)

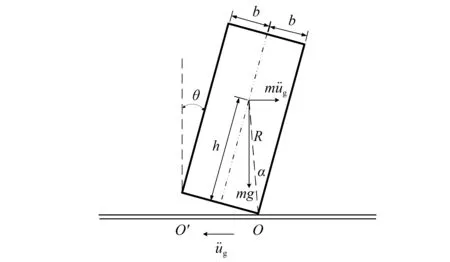
图1 浮放系统计算简图Fig.1 Computing model of freestanding system

根据静力平衡，当惯性力矩大于重力提供的抗倾覆力矩时试件启动摇摆，即

(3)

此外，接触面的摩擦因数μ还要满足发生摇摆运动的必要条件[14]

b/h<μ

(4)

馆藏文物一般以陶瓷器、珐琅器、木漆器以及有镀层或釉层的金属器为主，展台面的材料一般有亚克力、木材、布材等；上述两类材料间的摩擦因数一般不低于0.3，若试件发生以摇摆为主的运动，由式(4)估算出该类文物的质心高宽比一般大于3。

1.2 研究对象的选择——大高宽比浮放文物

浮放系统在地震作用下的运动状态主要可分为滑移和摇摆两大类，其中滑移运动在一定程度上可以通过摩擦做功消耗地震的部分能量，因此适当的滑移是有利的，保证文物不会滑落或碰到周围物体即可；而摇摆可能会直接引起浮放文物的倾覆，极有可能摔碎造成严重的损失。

在摇摆的每半个周期内，物体和台面就会碰撞一次，必然会损耗能量。设碰撞前的半个周期所对应的幅值摆角为θi，碰撞后的半个周期所对应的幅值摆角为θi+1，Ek,i和Ek,i+1分别为碰撞前后的动能，定义碰撞前后瞬间的动能之比为能量恢复系数r，可得

(5)

根据刚体冲击力学的理论，碰撞瞬间对旋转中心的动量矩守恒并与式(1)联立可得

(6)

由式(6)可知，r由试件的几何尺寸决定，对于矩形块体，其能量恢复系数与高宽比的关系如图2所示。

图2 能量恢复系数Fig.2 Energy recovery coefficient

可见高宽比越大的浮放文物，摇摆过程中通过碰撞耗能的比例越小。此外，对于高宽比越大的浮放块体，其几何特征角α越小，摇摆角超过该值而倾覆的可能性也较高。

综上所述，本文研究的“大高宽比文物”即为浮放状态下，受到地震作用时容易发生摇摆的一类物体。

2 浮放花瓶振动台试验

2.1 试验介绍

为探究浮放文物在水平激励下的基本运动规律，对陶瓷花瓶进行振动台试验，用拉力计测得花瓶与亚克力展台面的摩擦因数约为0.35，花瓶的基本物理参数如表1所示。

表1 浮放陶瓷花瓶的基本参数Tab.1 Parameters of freestanding ceramic vase

在花瓶顶面中心固定倾角姿态传感器监测花瓶的摇摆角，同时在振动台面上布置激光位移传感器监测花瓶的滑移量，并用加速度拾振器采集振动台面的加速度反馈信息。定义激励方向为X向，水平面内与其垂直的为Y方向，绕X轴的旋转角为UR1，绕Y轴的旋转角为UR2，试验布置及坐标规定如图3所示。

图3 试件及布置Fig.3 Test specimens and arrangement

分别输入水平单向的简谐波和地震波，简谐波的加速度幅值PGA(peak ground acceleration)调幅范围为0.10～0.35g，调幅梯度为0.05g；频率由1.0～3.0 Hz，调幅梯度为0.5 Hz；地震波选取El-Centro波和Taft波，时程曲线如图4所示。PGA由0.1～0.4g以梯度0.05g调幅。若试件出现快速倾覆则终止试验，每组试验重复3次，若出现不同结果，则补做试验至某相同结果连续出现3次为止。

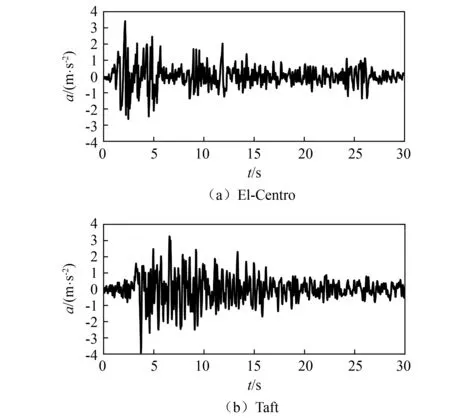
图4 输入的地震波加速度时程曲线Fig.4 Time history curve of acceleration of input seismic waves

2.2 简谐波下的试验结果及分析

花瓶在简谐波下的试验结果如表2所示。由于花瓶底面为圆形，在单向激励下可能出现扭转的现象，限于篇幅，部分摇摆时程曲线如图5所示。

表2 花瓶在简谐波下的试验现象Tab.2 Experimental results under simple harmonic waves

图5 简谐波下浮放花瓶的摇摆响应Fig.5 Rocking responses of freestanding vase under simple harmonic waves

在PGA均为0.25g而频率不同时，试件可能经少次摇摆就倾覆，也可能经多次摇摆随后倾覆。在一定范围内，简谐波频率越高，试件越难倾覆；相同频率下，PGA越大，试件越易倾覆。

2.3 地震波下的试验结果及分析

两条地震波下的试验现象如表3所示。与表2对比可知，相同PGA下的地震波和简谐波，简谐波更容易使文物花瓶发生摇摆和倾覆。

表3 花瓶在地震波下的试验现象Tab.3 Experimental results under seismic waves

WW/T 0069—2015《馆藏文物防震规范》中将不发生摇摆作为不发生倾覆的条件，根据其公式，取安全系数k0=1.2，得到不发生倾覆的PGA最大估计值为

(7)

试验结果表明：试件在PGA=0.25g以下无明显现象，当PGA=0.30g时发生摇摆，两条波的PGA达到0.35g和0.40g时发生倾覆，公式的估计值偏于保守。部分试验曲线，如图6所示。当PGA=0.3g时，两条地震波下的摇摆角都很小，但El-Centro波下的摇摆角要比Taft波的更大；当PGA=0.35g时，两条波下都发生了倾覆，但El-Centro波下发生倾覆的时刻要明显更早。

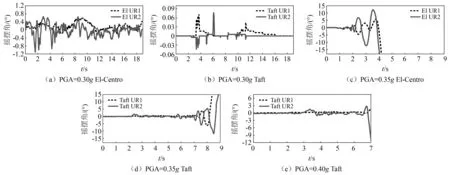
图6 地震波下浮放花瓶的摇摆响应Fig.6 Rocking responses of freestanding vase under seismicwaves

3 基于有限元的参数化分析

3.1 有限元模型的建立与验证

参考以往对摇摆系统动态有限元建模的研究[15-19]，选用ABAQUS 6.14/Explict软件作为分析平台。摇摆时文物和台面不发生大变形，因此材料均考虑为弹性，并用Rayleigh阻尼模拟浮放系统中所有能量耗散机制。

台面采用可变形体的C3D8R单元，花瓶采用S4R壳单元，网格属性中增强沙漏控制，接触为通用接触。根据以往研究的建模方法，切向选择罚函数控制的库伦摩擦公式，并且认为动静摩擦因数相等可以较好地模拟浮放系统接触界面的摩擦行为，法向选择“硬”接触，并允许接触后分离。

初始分析步中约束住台面的3个平动位移；除初始分析步外，共设置3个分析步：第一个分析步对整体施加重力；第二个分析步为静置分析步，用于消除重力激振的影响；第三个分析步释放X方向的约束，并在该方向上施加地震波，有限元模型如图7所示。

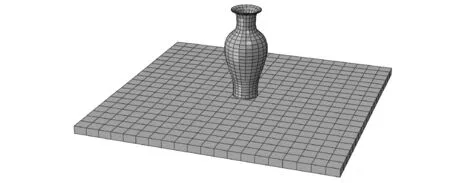
图7 有限元模型示意图Fig.7 Schematic picture of FEM

选取El-Centro波0.35g工况下的两条试验曲线与有限元结果对比，其中有限元模型的输入荷载按台面实际采集到的波进行输入，摩擦因数采取2.1节中通过静拉试验测得的数值0.35。对比结果如图8所示。整体上有限元与试验的结果吻合度较高，证明该建模方法有效。

图8 有限元与试验结果对比Fig.8 Comparison of FEM and experimental results

根据上述分析，影响浮放系统运动状态的因素可分为直接因素和间接因素两大类。直接因素是文物本体的性质(高宽比，几何形状等)，而间接因素包含放置条件(摩擦因数)以及激励特性。对于某个特定的文物，直接因素无法改变，文保工作者更关心的是如何改变放置条件(间接因素)从而更有效地保护文物。

因此，有必要基于数值计算，对地震加速度，展台面的摩擦因数以及展台面的倾斜程度进行参数化分析。

3.2 加速度对浮放文物运动状态的影响

将El-Centro波分别调幅至0.25g，0.30g，0.35g和0.40g，摇摆响应计算结果如图9(a)所示。随着PGA的增大，花瓶摇摆时程大体相似，但相位有所提前，当PGA达到0.40g时，试件发生倾覆。为精细化研究，在0.35～0.40g以0.01g再次调幅，结果如图9(b)所示。

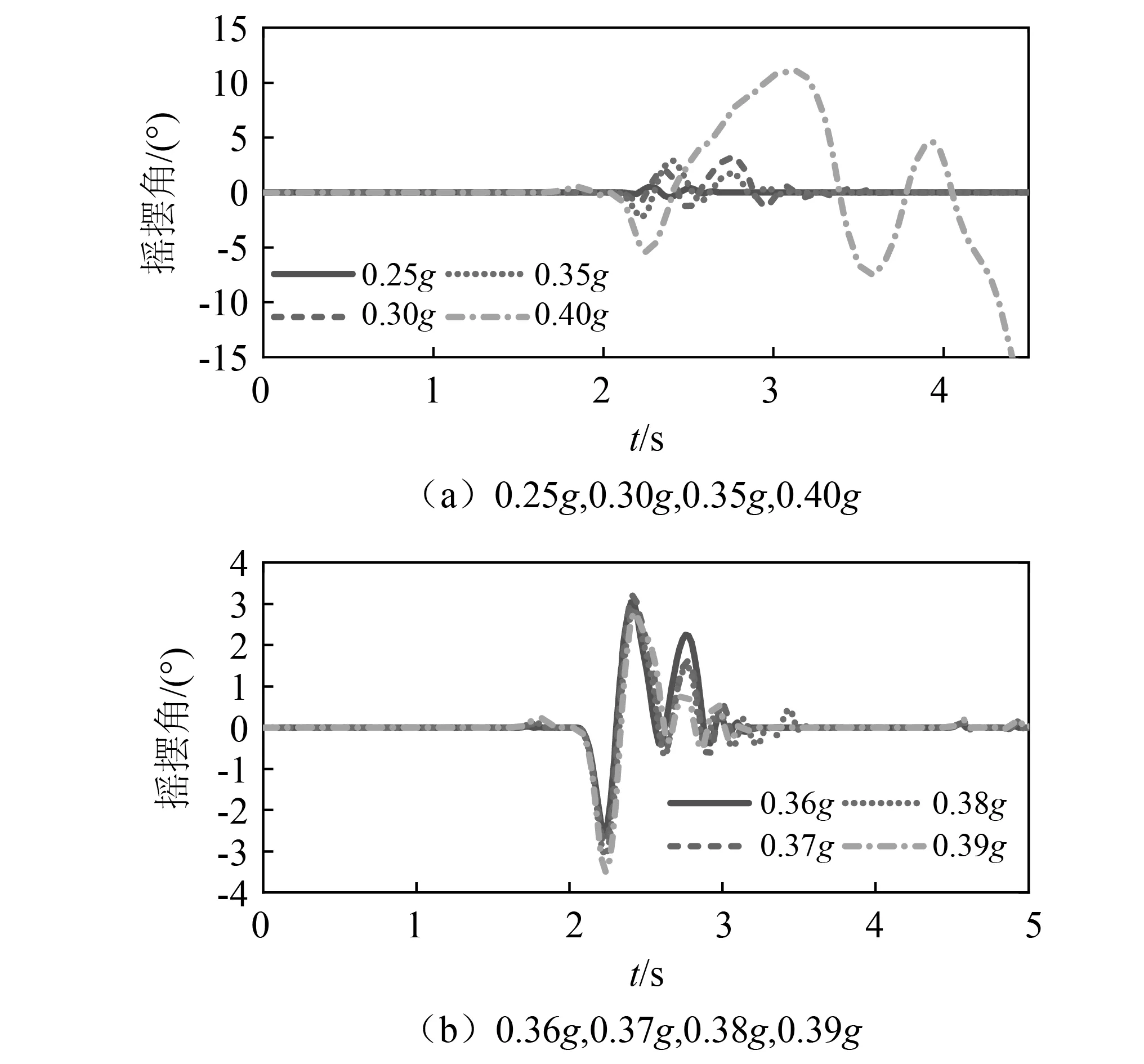
图9 El-Centro波不同加速度幅值下的摇摆角响应Fig.9 Rocking responses under El-Centro waves with different acceleration amplitudes

将试件底面中心点与台面中心点的水平位移差作为滑移量，其响应如图10所示。各工况下的滑移量与试件底面的尺寸相比均很小，最大的滑移量约为底面直径的1/220，因此可以认为发生了理想摇摆。此外，试件在激励加速度较大的时刻发生较明显的滑移，随后滑移到新的平衡位置。在μ满足摇摆的条件下，随着PGA的增大，系统由滑移转变为以摇摆为主的运动状态，并且随着PGA的增大，摇摆越明显。

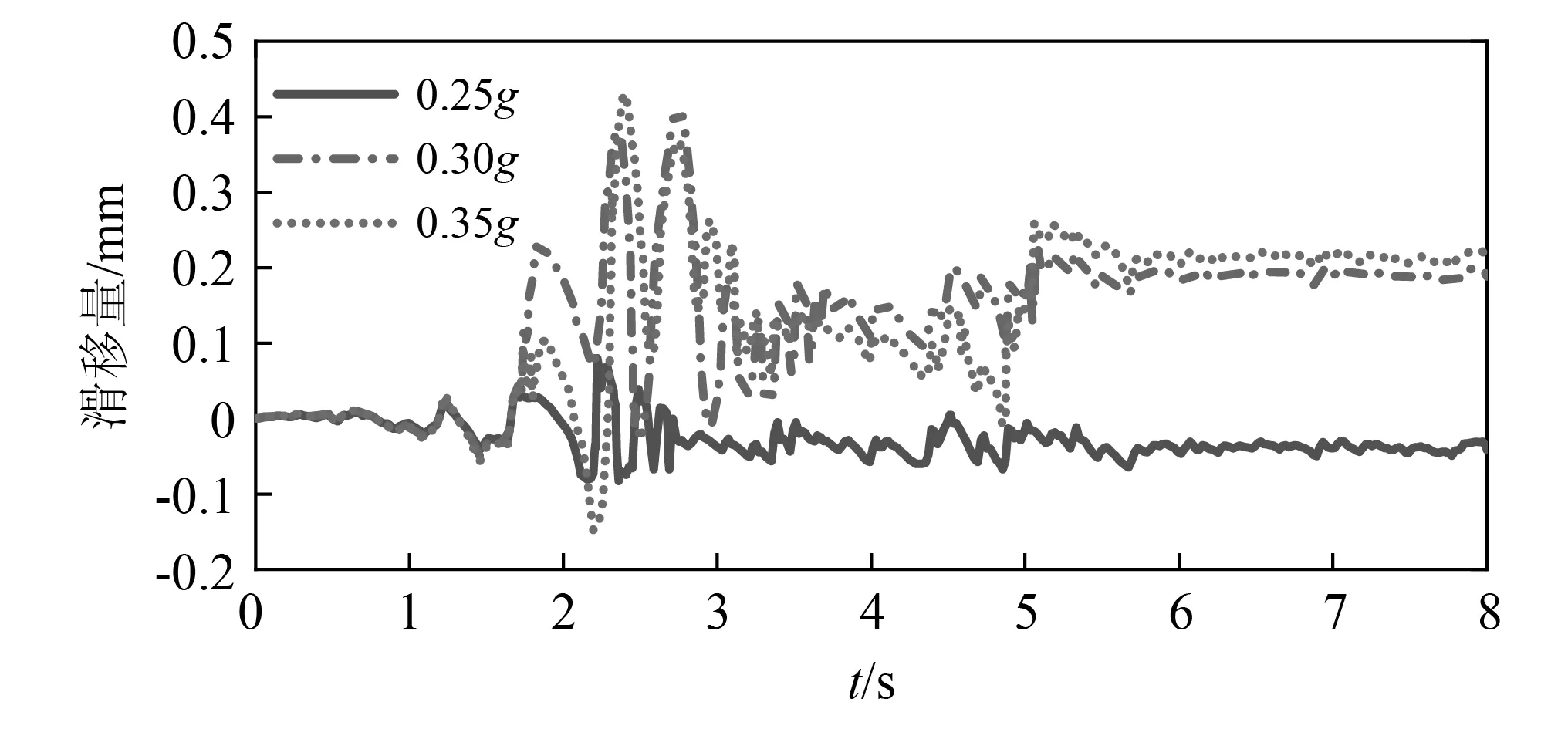
图10 El-Centro波不同加速度幅值下的滑移响应Fig.10 Slipe responses under El-Centro waves with different acceleration amplitudes

3.3 摩擦因数对文物运动状态的影响

在El-Centro波下，将ABAQUS软件中的μ值以0.1为梯度从0.1～1.0调幅。当PGA=0.3g时，不同摩擦条件下摇摆角响应如图11所示。当μ为0.1和0.2时，文物仅滑移；此后，随着μ的提高，前几次摇摆的曲线较为一致，随后整体趋势相近，但彼此存在相位差。整体来看，随着μ的提高，浮放文物的运动状态从纯滑移变为以摇摆为主，但摇摆角并不严格随着μ的提高而增大，摇摆角最大的情况并不是在μ=1时出现，而是在μ=0.4时出现。

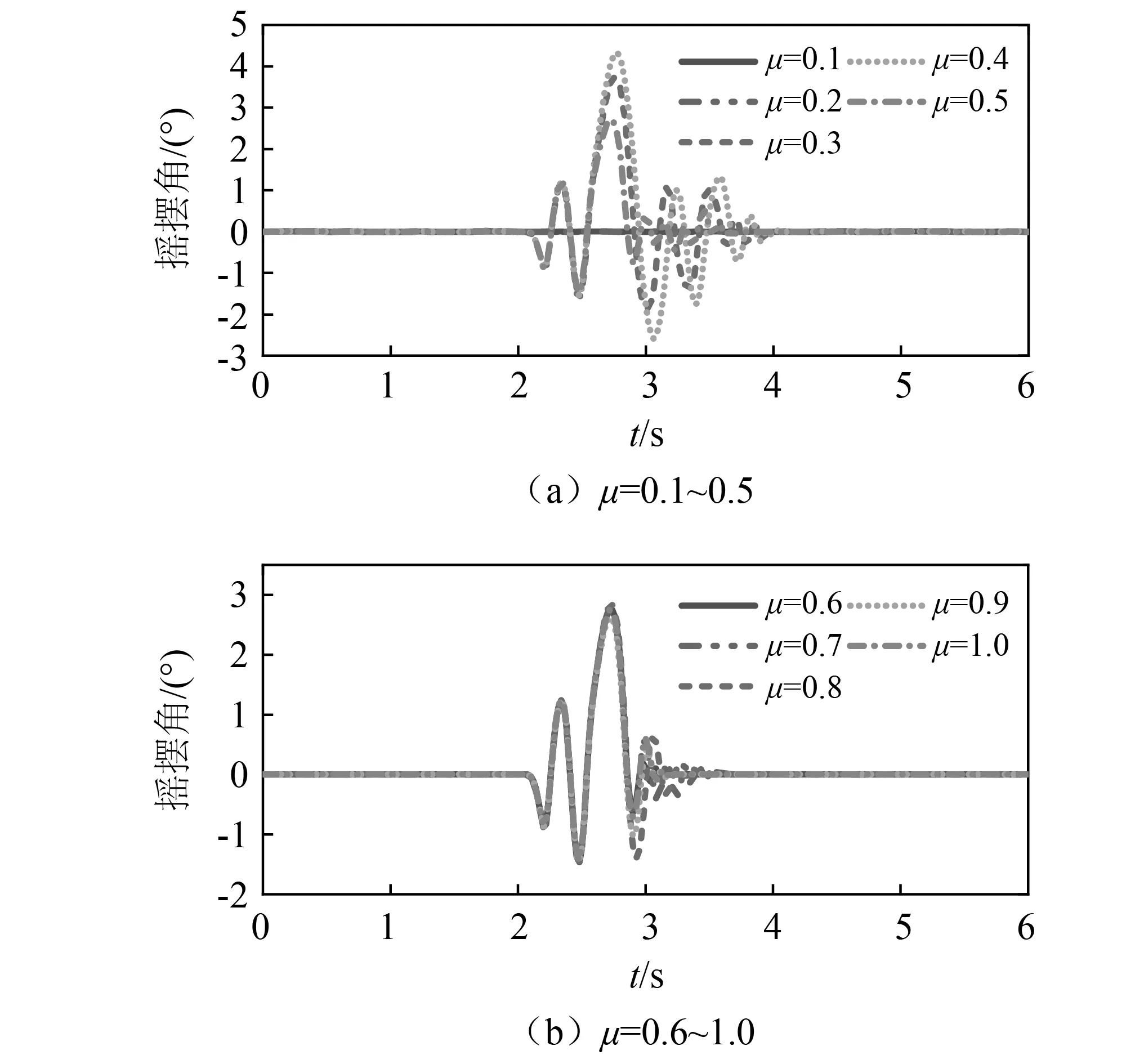
图11 PGA=0.3g时不同摩擦因数下的摇摆角响应Fig.11 Rocking responses under different friction coefficients at PGA=0.3g

滑移量响应如图12所示。当μ为0.1和0.2时，文物仅滑移，最大滑移量随着μ的提高而降低。当文物摇摆后，其最大滑移量降到0.4 mm以下，其中μ=1.0时的最大滑移量最小。相较于文物的几何尺寸，可以认为当文物发生明显摇摆时，运动状态主要受摇摆控制。此外，滑移变化是同步的，均在加速度较大处发生较大滑移，随后在新平衡位置继续运动。

当PGA=0.35g时，不同摩擦条件下的摇摆响应如图13所示。与PGA=0.3g时的规律类似。其中，摇摆角最大的情况出现在μ=0.5的工况下。

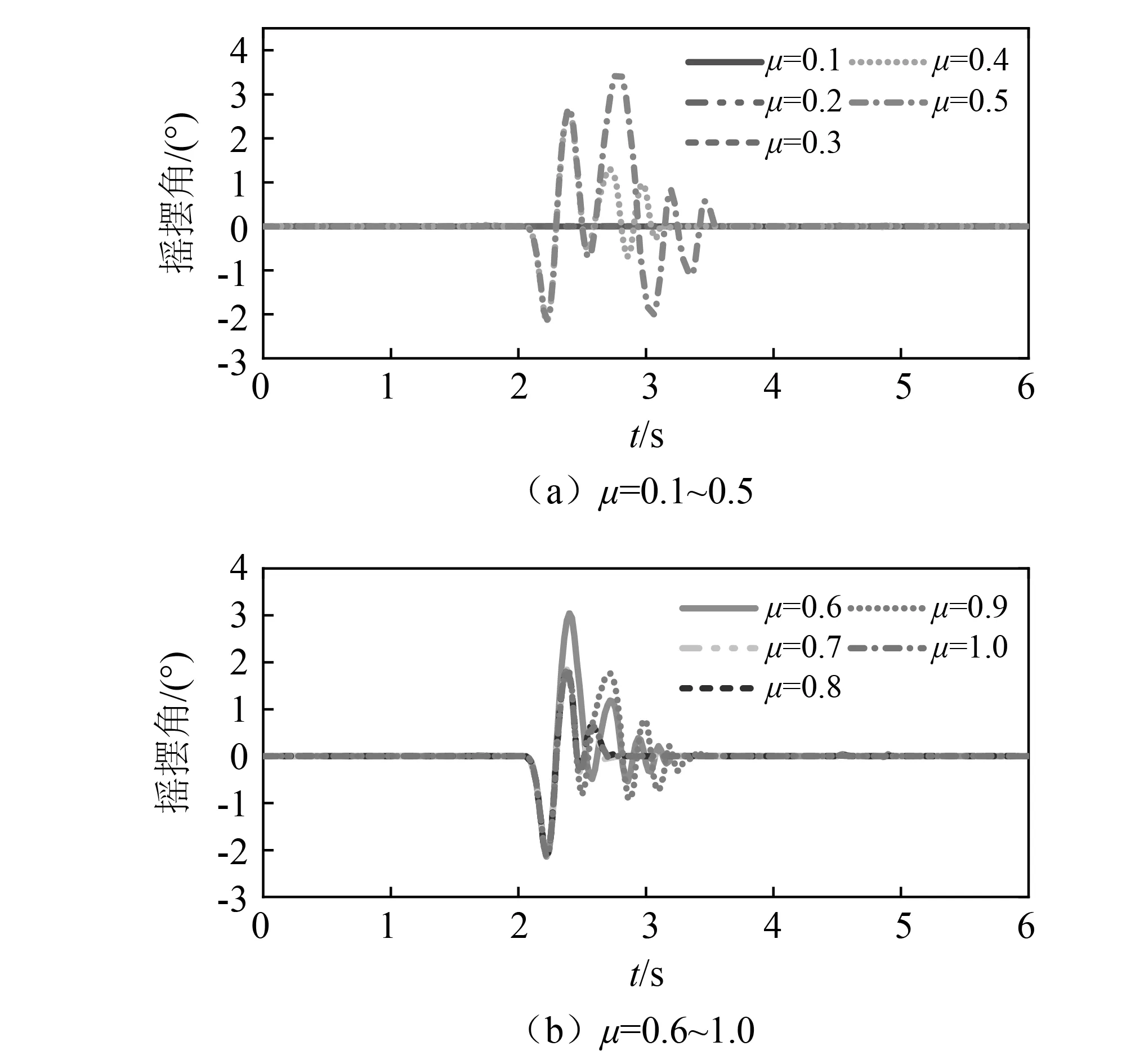
图13 PGA=0.35g时不同摩擦因数下的摇摆角响应Fig.13 Rocking responses under different friction coefficients at PGA=0.35g

PGA=0.35g时的滑移响应如图14所示。规律与PGA=0.3g的情况相似，滑移量最小的工况为μ=1.0下的工况。与图12对比可知：当系统运动状态以滑移为主时，相同的摩擦因数下，PGA越大，其滑移越明显；但当文物运动状态以摇摆为主时，滑移表现则出现非线性的特点，并不总是随着摩擦因数的提高而降低，但最小的滑移量均出现在μ=1.0的工况下。因此从整体上说，若希望降低浮放系统的滑移响应，最有效的措施是增大接触面的摩擦。

图14 PGA=0.35g时不同摩擦因数下的滑移量响应Fig.14 Slip responses under different friction coefficients at PGA=0.35g

在PGA= 0.4g的El-Centro波下，浮放系统可能发生倾覆，其最大滑移量和最大摇摆角如表4和表5所示。值得说明的是，对于文物发生倾覆的情况，最危险的不利状态是倾覆而非滑移，所以对此类工况的滑移量取为摇摆角达到α时刻之前的最大滑移量。

表4 摩擦因数对浮放文物滑移量和摇摆角的影响1Tab.4 Test results under different friction coefficients 1

表5 摩擦因数对浮放文物滑移量和摇摆角的影响2Tab.5 Test results under different friction coefficients 2

由表4和表5可知：随μ着的微小增加，滑移量大幅衰减同时摇摆现象加剧，其中μ=0.1和0.2的工况下，浮放文物以滑移运动为主，与式(4)的计算结果一致，在μ=0.3～0.5的工况下，浮放文物发生倾覆；但当μ提高达到0.6和0.7时，运动状态仅为摇摆而非倾覆；当μ=0.8～1.0时，运动状态又变为倾覆。综合上述所有工况可以得到：一个很光滑的摩擦条件可以有效地避免系统发生摇摆运动，但摇摆响应并不是随着摩擦条件越粗糙而越剧烈。

3.4 台面倾斜对文物运动状态的影响

在PGA=0.3g的条件下，将展台面沿着与地震累计位移方向相同的方向(正向)、负向及面外的正交方向分别倾斜一个较小角度，计算出El-Centro波下浮放文物的相对摇摆角响应，如图15所示。Taft波下的摇响应，如图16所示。

无论台面朝哪个方向倾斜，随着倾斜角度增加，摇摆响应曲线在幅值和相位上均呈现出很强的非线性变化规律。在El-Centro波下，对于正向倾斜的情况，见图15(a)。当倾斜角为1°和2°时，相比于未倾斜的情况，其最大摇摆角反而减小，但当倾斜角达到3°时，试件发生倾覆；对于负向倾斜的情况，见图15(b)：负向的台面倾角使得文物的正向摇摆角减小，同时负向摇摆角增加，所以在一定范围内，台面的负向倾角对抗倾覆是有利的；对于正交方向倾斜的情况：倾斜角度越大，摇摆响应UR2也逐渐明显，见图15(c)；且伴随一定的面外扭转运动，见图15(d)。

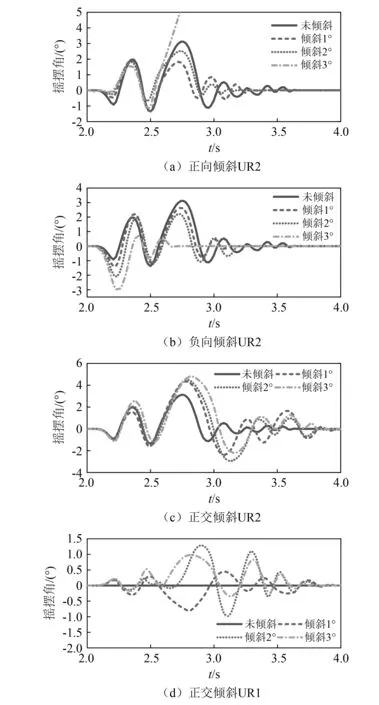
图15 El波下浮放文物的摇摆响应Fig.15 Rocking responses under tilting tables

Taft波下浮放文物的摇摆响应，如图16所示。在Taft波下，正向倾斜仅1°时就会发生倾覆，见图16(a)。而负向倾斜会使摇摆响应在8 s附近减小，同时在5 s附近增大，见图16(b)。在正交方向上存在倾斜时，X和Y两个方向上均存在非线性的响应特征，当台面倾斜达到5°时，浮放文物发生倾覆。

综上所述，台面的水平程度和倾斜方向也会不同程度地影响浮放文物的运动状态，由于地震波是多方向且不可预测的，无法保证台面总朝着有利方向倾斜。因此，为了避免扭转运动，最大程度上保证浮放系统的安全储备，要尽可能地保证台面水平。

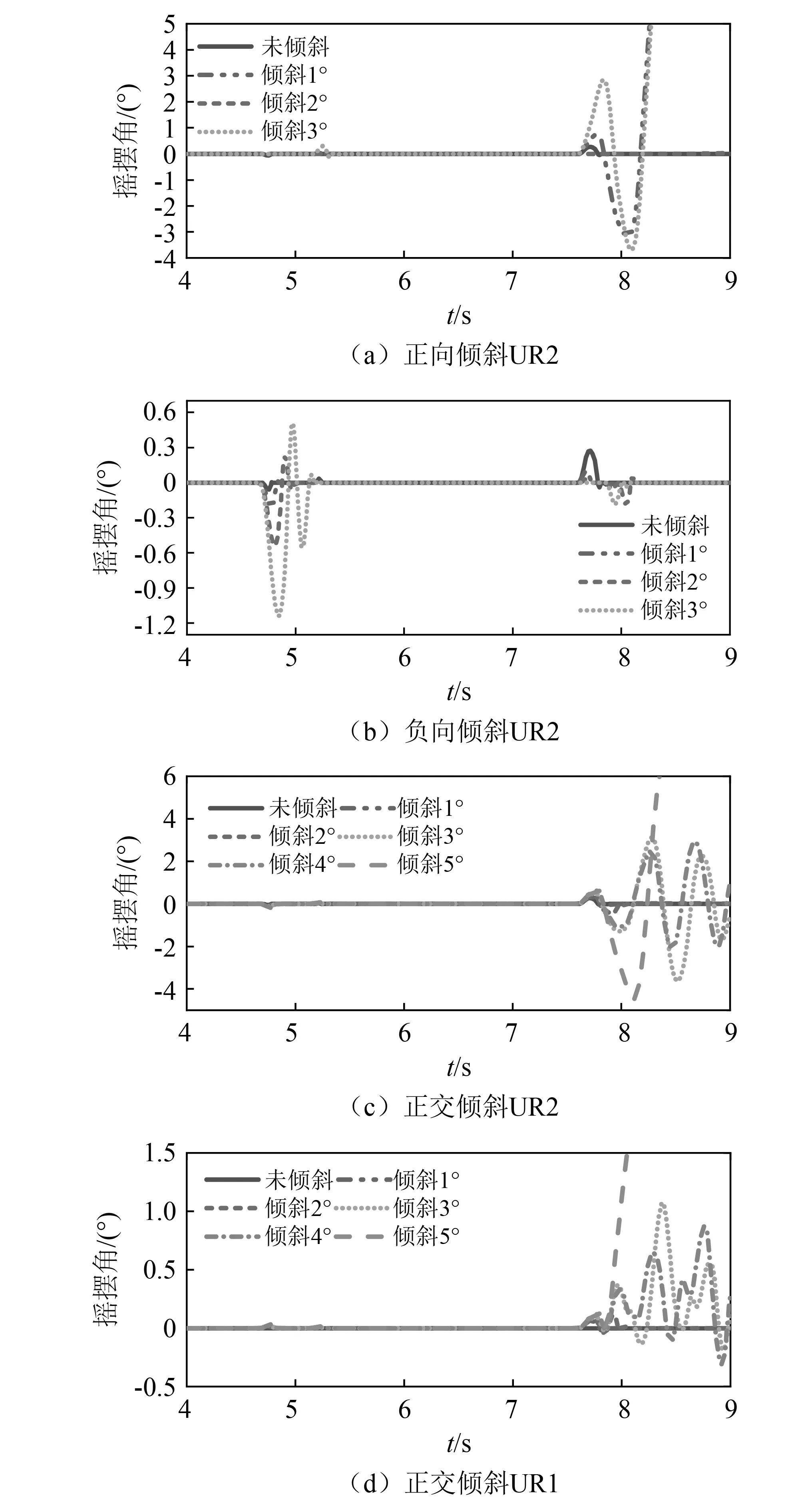
图16 Taft波下浮放文物的摇摆响应Fig.16 Rocking responses under tilting

4 结 论

(1) 本文通过振动台试验和基于有限元的参数化分析得到了大高宽比浮放文物运动状态的影响因素及其影响规律，为大高宽比浮放文物的展出工作提出了建议。其中根据理论计算，定义了大高宽比浮放文物为浮放状态下易发生以摇摆为主的运动的一类浮放文物，其质心高宽比一般应大于3。