一类具有常数移民特征的时滞SEI 传染病模型的周期解
刘 娟,潘玉荣,张子振
(1.蚌埠学院 数理学院,安徽 蚌埠 233030;2.安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
在新冠疫情持续蔓延的背景下, 关于传染病的研究已受到世界各国的重视, 医学科学的最新研究成果已帮助人们更好地控制了疫情的传播。
在研究生物数学过程中, 人们常常利用数学模型研究一些生物现象, 利用动力学思想研究传染病的传播规律, 数学模型已成为分析疾病传播的有效工具[1-2]。
最近, 一些学者利用数学模型分析了传染病的传播状况, 从数学的角度提出控制传染病传播的建议。 朱晶[3]研究了基于Logistic 增长和心理作用的SIR 传染病模型,讨论了模型解的渐近行为。 在SIR传染病模型中, 要求恢复者对疾病具有永久的免疫力,这显然不符合实际情况,原因是感染者康复后仍有可能再次被感染。 王俊荣等[4]、李小妮等[5]和李文轩等[6]提出了更符合实际的SIRS 传染病模型。 考虑到传染病具有潜伏期,一些学者在SIR 和SIRS 传染病模型的基础上,通过引入潜伏者状态研究了SEIR传 染 病 模 型[7-8]和SEIRS 传 染 病 模 型[9-10]。 但 以 上 研究涉及的传染病模型均忽略了潜伏者和感染者的移民特征。 例如,艾滋病和新冠肺炎都具有移民特征,尽管各国对出入境人员采取了疫情防控措施, 但仍有少量感染者会进入这些国家。 为此,Khan 等[11]提出并研究了易感者、 潜伏者和感染者均具有常数移民特征的SEI 传染病模型

1 Hopf 分岔的存在性


2 分岔周期解的性质



3 数值仿真
选取参考文献[11]中的参数BS= 0.6,BE=0.1,BI= 0.3,µ= 0.026,γ= 0.1,β=0.001,可得模型(2)的特例


图1 τ=16.586 8时模型(30)的局部渐近稳定性
当τ>τ0= 18.509 7时,模型(30)在P*(12.186 7,3.040 8,23.234 0)是非局部渐近稳定的,且产生Hopf分岔。 仿真效果如图2 所示。 通过计算可得λ′(τ0) = 0.004 39 − 0.000 26i,C1(0)= − 0.000 69+0.029 46i。根 据式(29)可以得到µ2= 0.157 17 >0,β2=−0 .001 38< 0,T2=− 0.00176 <0。因此由定理2可知,模型(30)在τ0=18.509 7处产生的Hopf 分岔是超临界的,分岔周期解是稳定递减的。
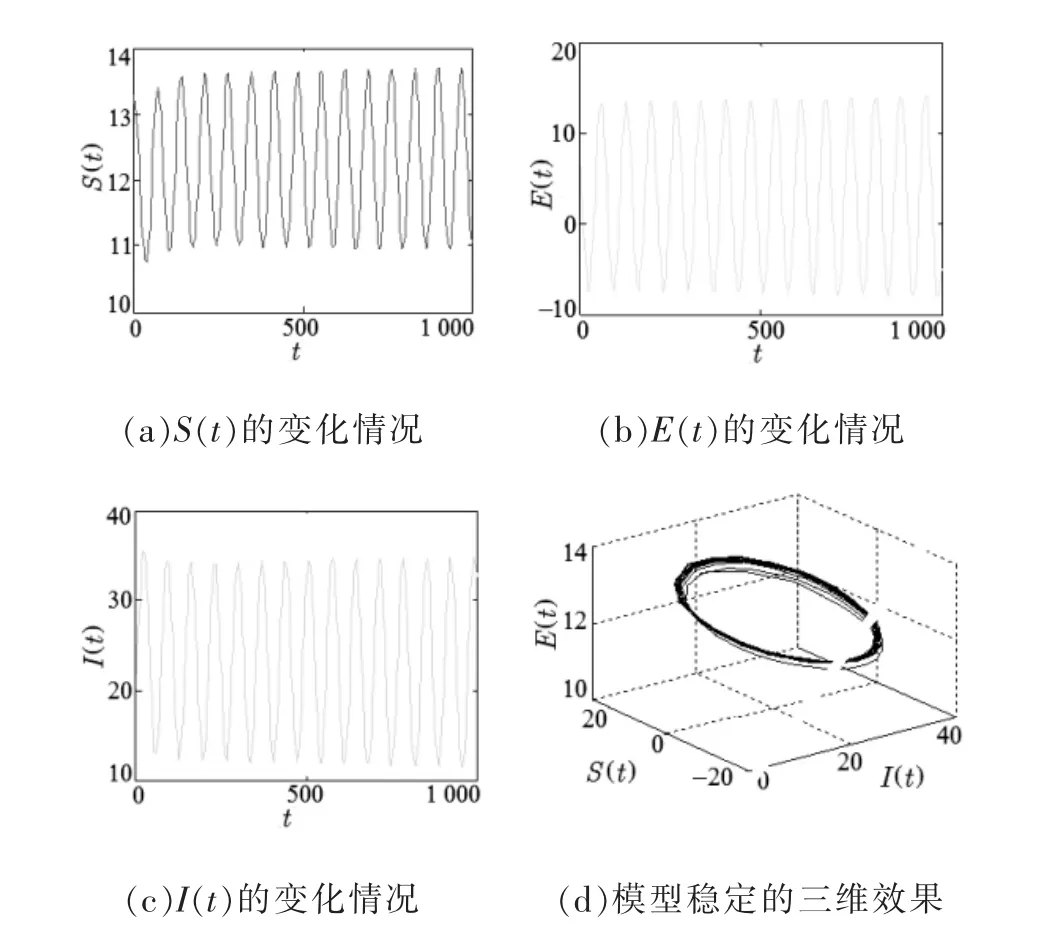
图2 τ =21.495 3时模型(30)的非稳定性
4 结论
在本文中,我们研究了一类易感者、潜伏者和感染者都具有移民特征的时滞SEI 传染病模型, 将疾病的潜伏期时滞作为分岔参数, 导出了模型局部渐近稳定和产生Hopf 分岔的充分条件,还研究了分岔周期解的方向、稳定性及周期大小,通过仿真示例验证了所得结果的正确性。
本文的研究结果表明, 当疾病的潜伏期时滞较小(低于临界值τ0)时,模型处于理想的稳定状态,这有利于疾病传播的控制。 当潜伏期时滞超过临界值τ0,模型将处于非稳定状态,并产生Hopf 分岔,模型中的易感者、潜伏者和感染者将进入周期震荡状态,这不利于疾病传播的控制。

