绿色基金视角下风险度量模型的实证对比探究

庹林华，陈 涛

(沈阳化工大学 经济与管理学院，辽宁 沈阳 110000)

1 引言

根据证券投资基金业协会数据，2021年国内绿色基金相关企业注册量从2010年的6家增长至52家，近5年绿色基金数量的平均增长率达到了40%，展现出巨大的市场潜力。随着“碳达峰”“碳中和”愿景的提出，我国未来预计将会成立更多的绿色基金。但我国绿色基金起步晚，发展时间短，整体规范性不足。实操中存在着筹资、投资两头难的问题，基金投向的各种绿色产业大多数投入期限长、投资回报率偏低，存在着很大不确定性。目前在金融风险度量方面的研究多是集中于整个金融市场，或是股票市场。基金由于收益较低，一般被为风险较小的投资方式。当前国内的政策发展环境下，绿色基金呈现出巨大势头，因此对绿色基金的风险不应该简单忽视。

2 常用金融风险度量模型

2.1 在险价值VaR模型

在险价值VaR模型，指在特定的时间长度和给定概率水平下，正常市场环境中，某金融资产或者投资组合在未来一段时间内的最大可能损失值。VaR模型一般计算出来是一个负值，负号代表损失。VaR模型的局限性是，并没有利用完整的分布信息而只使用整个分布上的一个点，因此容易产生滞后性，甚至无法识别发生重大风险的情况。VaR模型可以衡个体风险，无法识别各金融机构之间的相互影响。

2.2 条件在险价值CVaR模型

CVaR模型是假设某个资产的收益为x，损失为-x，则CVaRα(X)=E(-X|-X≥VaRα)，该模型度量了尾部极端风险的均值。CVaR模型的变动灵敏，更加能反映市场的变化，适用大规模的资产组合的风险度量。CVaR模型是传统VaR模型的修正和优化，但始终是在传统VaR模型计算出的值上进行测度的，因此会影响到CVaR模型计算的有效性。

2.3 POT模型

POT模型是极值理论在风险测度运用中的其中一种，全称是阈值尖峰模型。极值理论是处理与概率分布的中值相离极大的情况的理论，常用来分析概率罕见的情况。一般用于研究很少发生，但一旦发生却会有巨大影响的随机变量极端变异性的建模及统计分析方法，非常适合金融市场风险复杂多变的情形。POT模型假设收益分布的尾部服从广义帕累托分布，确定收益分布的阈值，从阈值开始为尾部数据集建立风险计算模型。局限性在于阈值确定的高低会影响结果的准确性。

2.4 ES模型

ES模型是指预期损失，表示在事先给定的分位数下，小于此分位数所对应收益的尾部损失的平均值，是CVaR模型上的一种改进。ES模型与CVaR模型的联系与区别是，若损失X的密度函数是连续的，则ES模型的结果与CVaR模型的结果相同；若损失X的密度函数是不连续的，则两个模型计算出来的结果有一定差异。局限性是容易因传统VaR模型的计算结果而影响模型的有效性。

3 实证分析

为了更加客观、精确地反映实证结果，将不考虑疫情因素的影响，以兴全绿色投资混合LOF基金2019年1月1日至12月31日在相关网站公布的每日增长率代表收益，剔除无效数据后共有236个数据为样本。由计量软件分析，该每日增长率序列的均值为0.001956，中位数0.0018，最大值0.0438，最小值-0.0489，标准差0.012018。偏度0.294679大于0，为右偏分布形态，峰度4.727064大于3，其分布凸起程度大于正态分布凸起程度，呈尖峰状态。同时，J-B统计量远大于临界值0。因此，兴全绿色投资混合LOF基金的日增长率序列具有尖峰厚尾特征，不能用正态分布来拟合此收益序列。

观察EViews中每日增长率数据的Line&Symbol图，可以看出该数据序列具有波动集群现象，即收益的巨大变化通常伴随着进一步的巨大变化。继续对该序列进行ARCH检验，残差平方项的P值为0.1526未通过显著性检验，即残差平方不能解释下一期的残差平方，没有显著的ARCH效应。因此，该序列不能进行波动率建模。在接下来的VaR等风险度量方法应用中，本文将采取其他方法。

对日增长率序列进行ADF平稳性检验。ADF值为-12.25157，分别小于显著性水平10%、5%、1%的临界值，能拒绝存在单位根的原假设，即该时间序列是平稳的。

3.1 VaR模型

本文采用Monte Carlo法计算VaR值。该方法的优点是不受金融工具复杂性影响、适用于非正态分布如尖峰厚尾，且估算精度较好，缺点是计算量较大。给定风险X和置信水平α下，在险价值VaR模型表示为：VaRα(X)=inf{x∈R,Fx(X)≥α}。根据计量软件分别在置信水平位95%和99%对日增长率序列进行VaR测度，进行了1000次蒙特卡罗模拟后得到结果VaR0.95=0.01753，VaR0.99=0.02517。进一步通过VaR值与损失均值之差，可得单个资产的经济资本度量值，结果分别为EC0.95=0.02578、EC0.99=0.03342。

3.2 CVaR模型

同时，根据CVaR值与损失均值之差，得到相应的经济资本度量值，结果分别为EC0.95=0.01176、EC0.99=0.02115。

3.3 POT模型

极值理论有两类模型，其中样本极大值模型(也称BMM模型)需要采集大量的数据且主要适合处理季节性明显的数据，不适合本文所采集的数据。本文采取极值理论的另一模型，阈值尖峰模型，简称POT模型，该模型描述的是超过某阈值的大量观察值的行为。把超越阈值是数据选做极值，当阈值充分大时，则这些选出的数据极值的函数分布收敛于广义帕累托分布，公式描述为：

3.4 ES模型

ES模型是指在一定的置信度水平下，损失超过 VaR 模型的条件下，投资组合遭受的平均损失，即期望损失。为了提高ES模型的准确性，将本文的蒙特卡罗模拟法来计算的VaR值与将广义帕累托分布计算的 VaR值分别应用到ES模型中并进行比较，比较结果如表1所示。

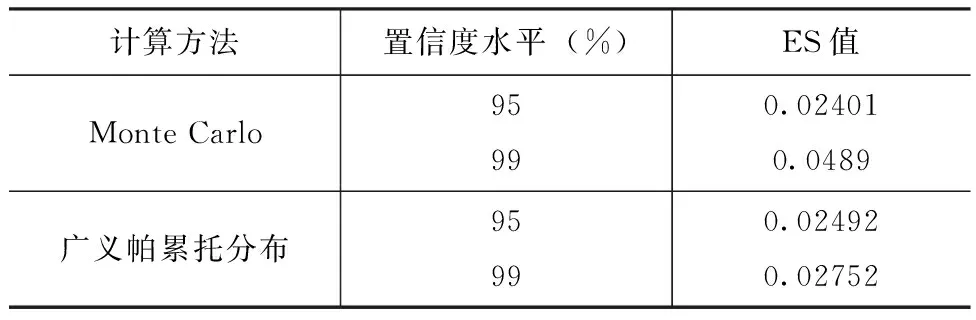
表1 不同算法下的ES模型比较

表1中可看出，两者在95%置信度水平下的ES值相差不大，99%置信度水平下蒙特卡罗法下的ES值更大一些。对于规模不大的组合资产而言，95%置信度下两种计算方法下的ES模型并无太大差别，随着置信度水平的提高，越精细化的计算方法所得出ES值也将更小。

3.5 失败率检验

在给定T天、t为超出VaR数目，若失败率

表2 不同模型的失败率检验

本文以波动较为剧烈的前100天为总天数。由表2结果，除了CVaR模型外的其他模型在不同的置信度水平下的失败率均在5%以下，并且失败率均差距不大。本文认为在短期内对规模不大的组合资产进行风险度量，选择ES模型、VaR模型或者POT模型比较合适。

3.6 VaR模型、CVaR模型、POT模型结果对比

由对比结果(见表3)可知，在短期内并且相同的置信度水平下，VaR模型的风险测度值和经济资本值均比CVaR模型的相应值要高，原因在于,CVaR模型更适合有足够样本且长期的风险度量。相同置信度水平下，POT模型风险测度值与经济资本度量值排在其他模型中间，并且相差不大，可以说比较综合全面。这是因为POT模型假设收益序列的尾部分布服从广义帕累托分布，并且也考虑到了风险厌恶者的偏好，与金融资产普遍存在的尖峰厚尾的特征分布相符，因此准确性更好。

表3 VaR模型、CVaR模型、POT模型结果对比

4 结论

本文以绿色基金市场中的兴全绿色投资混合LOF基金为研究对象，从VaR模型、CVaR模型、POT模型以及ES模型的角度对该基金短期内的风险进行度量，并将测度结果进行对比。综合来看，基于极值理论的POT模型由于考虑方面更加全面，因此在各模型的结果比较中表现更加良好，风险度量结果也比较适中。而由于受国内绿色基金本身规模不大的限制，CVaR模型在此次结果比较中表现稍差，进一步验证了对规模不大的金融组合资产进行度量时，选择VaR模型、POT模型或者ES模型是比较好的选择。