2022年高考理综全国乙卷25题第（2）问的解法探析

党维军，任爱红

渭南市瑞泉中学，陕西 渭南 714000

1 原题再现

如图1（a），一质量为m的物块A与轻质弹簧连接，静止在光滑水平面上；物块B向A运动，t=0时与弹簧接触，到t=2t0时与弹簧分离，第一次碰撞结束，A、B的 v-t图像如图1（b）所示。已知从t=0到t=t0时间内，物块A运动的距离为0.36v0t0。A、B分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞，之后A再次滑上斜面，达到的最高点与前一次相同。斜面倾角为θ（sinθ=0.6），与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求

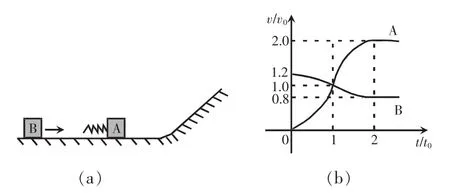
图1 原题题图

（1）第一次碰撞过程中，弹簧弹性势能的最大值；

（2）第一次碰撞过程中，弹簧压缩量的最大值；

（3）物块A与斜面间的动摩擦因数。

2 题意分析

该题考查了一个双弹簧振子的简谐振动模型。已知物块A质量为m，由题给的v-t图像可知：t=0时物块A、B的速度分别为0和1.2v0，至t0时刻二者速度相等，均为v0，且物块A运动的距离为0.36v0t0。前两问只涉及光滑水平面上的运动，根据动量守恒定律可得质量关系mB=5m，结合能量守恒定律可解得第（1）问弹簧最大弹性势能。第（2）问求第一次碰撞过程中，弹簧压缩量的最大值。

3 第（2）问解法探析

3.1 积分思想

物块A、B受轻弹簧的弹力大小相等、方向相反，根据牛顿第二定律可知加速度大小满足aA=5aB，且加速度都随时间变化。规定水平向右为正方向，在某时刻t（t≤2t0）二者速度可表示为：，联立可得

物块A、B组成的系统合外力为零，系统动量守恒，即 mB×1.2v0=mvA（t）+mBvB（t），代入质量关系mB=5m，也可以得到（1）式。

对（1）式在0到t0时间内定积分可得

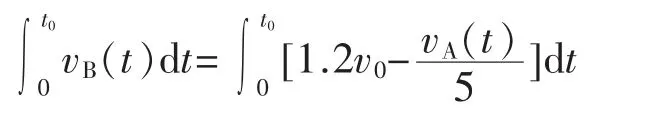
即0到t0时间内二者位移满足。代入已知条件sA=0.36v0t0，可得sB=1.128v0t0，根据位移关系可得弹簧的最大压缩量Δlm=sB-sA，代入数据可得Δlm=0.768v0t0。

3.2 质心参考系

设弹簧原长为l0，t=0时，质心C的位置如图2中所示，设物块B到质心的距离为l1，物块A到质心的距离为l2，则有mBl1=ml2，解得，质心相对地面的速度因物块A、B组成的系统合外力为零，根据质心运动定理[1]可知，质心相对地面的加速度aC=0，且以速度v0向右做匀速直线运动，为惯性参考系。

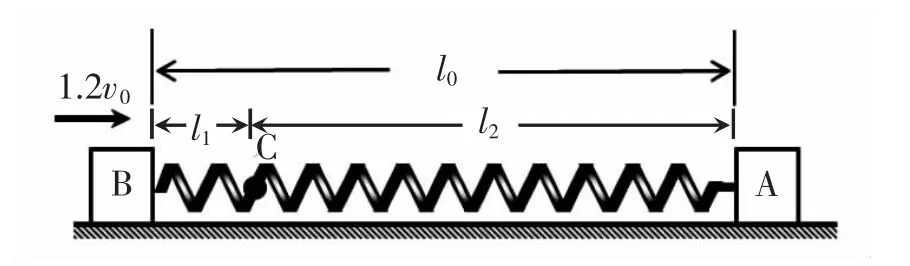
图2 系统运动分析

3.2.1 质心参考系下确定位移关系

t=0时质心C把该轻质弹簧分为自然长度为1:5的左右两部分，根据弹簧串联的规律[2]可知两部分劲度系数之比为5:1，记为5k和k。设t0时刻物块A、B相对质心C移动的距离分别为XA、XB，因轻弹簧两端弹力大小始终相等，则有：kXA=5kXB，即XA=5XB。已知0到t0时间内物块A相对地面的位移sA=0.36v0t0，根据位移的牵连关系有

代入后解得 XA=0.64v0t0，则 XB=0.128v0t0，压缩量的最大值Δlm=XA+XB=0.768v0t0。

3.2.2 质心参考系下的简谐振动

以质心为参考系，则质心C是静止的，物块A、B 的初速度分别变为：VB0=1.2v0-v0=0.2v0、VA0=0-v0=-v0，均是以质心C为固定端做简谐振动的弹簧振子[3]，t=0时刻均经过平衡位置，设物块A、B的运动学方程为

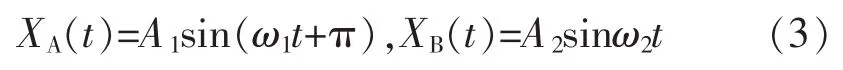
二者振动方向始终相反，且初始时物块A向左运动，故初相位为π。由弹簧振子的圆频率公式可得 ω1=ω2，即二者为同频率的简谐振动。由图1（b）知t0时刻弹簧压缩量最大，即A、B简谐振动的周期均为T=4t0，将其代入，可得A、B的圆频率均为。弹簧振子从平衡位置经四分之一周期至振幅最大处，动能转化为弹性势能且总能量守恒，故有，其中vm为平衡位置的速度，可得振幅，代入圆频率和各自的初速度，可得物块A、B的振幅分别为。压缩量的最大值，代入π可得Δlm≈0.7639v0t0。与前文答案不一致，原因是题给条件0.36v0t0取了近似，根据位移关系sA=-A1+vCt0，可得0到t0时间内物块A相对地面的位移，代入π可得sA≈0.3634v0t0，同理可计算出物块B相对地面的位移，代入 π可得sB≈1.1273v0t0。运用简谐振动规律可不用题给条件sA，直接算出准确的结果。

下面对题给v-t图像进行说明。对（3）式所示的运动学方程关于时间求导，可得A、B在质心参考系下的速度

代入初始条件：t=0时的速度VA0=-v0、VB0=0.2v0及，同样可解得振幅。根据速度的牵连关系：物块A、B相对质心的速度加质心相对地面的速度等于物块相对地面的速度，即vA（t）=VA（t）+vC，vB（t）=VB（t）+vC，代入对应结果可得

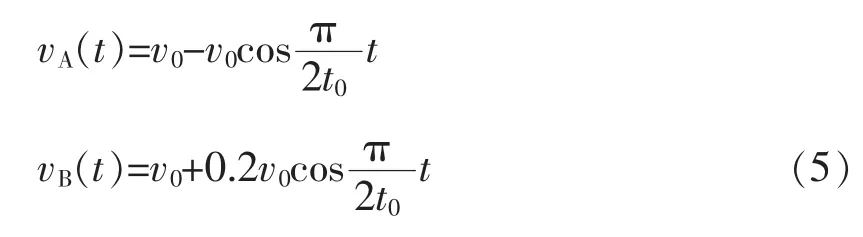
（5）式就是题给v-t图像的函数表达式，容易看出该图像是周期相同、相位差为π的两个余弦函数图像向上平移v0后得到的。确定了v-t图像的规律后，可根据定积分计算图像面积来求解第（2）问，此处不再赘述。

3.2.3 求弹簧劲度系数

设题中弹簧劲度系数为k0，可看作是由劲度系数为5k和k的左右两部分串联而成，联立，可得，根据弹簧串联规律有，解得，根据弹性势能公式，代入第（1）问的结果，同样可得。

3.3 非惯性参考系

为了方便，以物块A为参考系研究物块B的运动。因A受弹力具有加速度，故A为非惯性参考系。以A为参考系B的初速度仍为1.2v0，设经时间 t（t≤2t0）， B 相对 A 的位移记为 x（t），则弹簧弹力为 F=k0x（t），A 的加速度为，方向向右。根据直线加速非惯性系中的动力学方程有：-k0x（t）+5m（-aA）=5maBA，其中 5m（-aA）为惯性力，aBA为物块B相对物块A的加速度，整理得，可见以A为参考系物块B的运动仍是简谐振动，由题可知t=t0时弹簧压缩量最大，则B简谐振动的周期仍为4t0，圆频率仍为。 设运动学方程为 x（t）=A3sinωt，A3为振幅，即弹簧的最大压缩量，初速度即平衡位置的速度，故有，解得。

4 平均力法的错因分析

平均力法的解题过程如下，设FA、FB为0到t0时间内弹簧对A、B的平均力，根据动能定理分别有

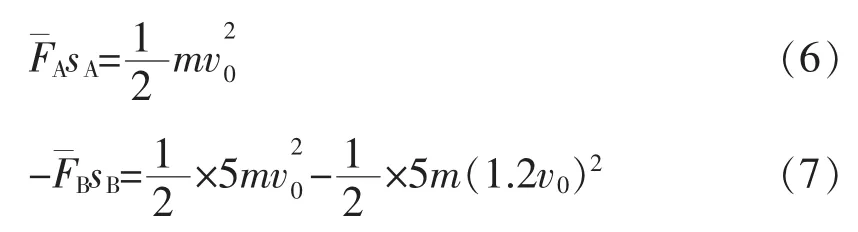
因弹簧两端弹力大小时刻相同，故平均力大小相等

联立（6）（7）（8）式可得 sB=2.2sA，弹簧最大压缩量 Δlm=sB-sA，代入 sA=0.36v0t0，可得 Δlm=0.432v0t0，与正确答案不同。

该法的错因分析如下：物体在方向不变的力的作用下做直线运动，平均力的计算分两种，一种是对时间的平均值，用于计算力的冲量；一种是对位移的平均值，用于计算力做的功。

就本题而言，在0到t0时间内对A、B分别应用动量定理有，解得，故弹簧两端弹力对时间的平均值相等。显然（6）（7）两式中的平均力应该用力对位移的平均值，因弹簧对A、B做的功不同，且A、B相对地面的位移也不同，那么平均力是否相同？将前文得到的结果sA≈0.3634v0t0和sB≈1.1273v0t0分别代入（6）（7）两式，解得，可见弹簧两端弹力对位移的平均值不相同，所以该方法的（6）（7）两式并没有问题，错误在（8）式，混淆了两种平均力。

另一种观点认为从t=0到t=t0时间内弹簧从原长变为最短，两端的弹力均从0变为最大Fm，平均力都等于。如果力随时间（位移）线性变化，则力对时间（位移）的平均值相同，本题中力随时间和位移都不是线性变化，故该结论不适用。