等效电源法巧析电路问题
赵 明
重庆市巴蜀中学校,重庆 400013
在电源内阻不能忽略的情况下,对于某些较为复杂的闭合电路,我们在分析电路中某部分电阻的电流、电压、功率等物理量的变化以及某些实验中的误差时,往往会出现复杂的数学运算,有时还会出现函数求极值等数学技巧问题,从而使问题变得繁琐,把物理问题变成了数学问题。本文利用等效电源[1]的思想处理电路问题,可以节约大量的数学运算时间,回归物理问题的本质,使物理问题简单化。
1 两类常见的等效电源问题
由闭合电路欧姆定律E=U+Ir可知:当I=0时,外电路断开,电源电动势数值上等于此时的路端电压,即E=U断;当U=0时,外电路短路,电路中的短路电流,可得。
因此,在把电路中的其他电阻和电源一起看成一个等效电源时,我们可以通过上面的方法得到下面两类情况下等效电源的等效电动势E'和等效电阻r',两者之间满足关系。
1.1 电源和一定值电阻R串联组成等效电源
如图1所示,此等效电源两端ab断开时,Uab=E,所以等效电动势E'=Uab=E。

图1 等效电源1
1.2 电源和一定值电阻R并联组成等效电源
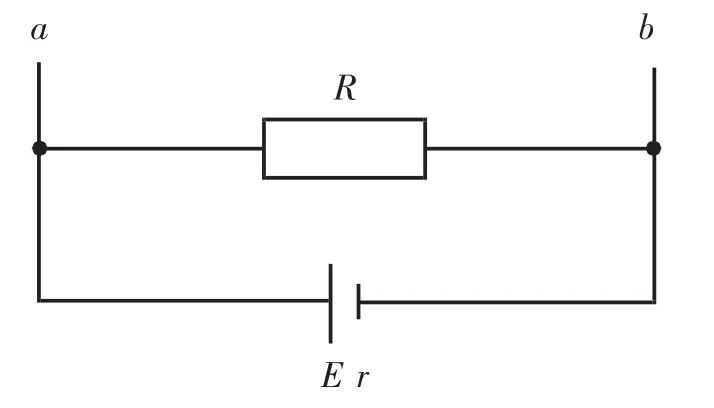
图2 等效电源2
2 滑动变阻器的功率最大问题
2.1 电源的最大输出功率结论
如图3所示,对于求解电源的输出功率,我们通常的解法是,对于纯电阻电路,结合闭合电路欧姆定律,有
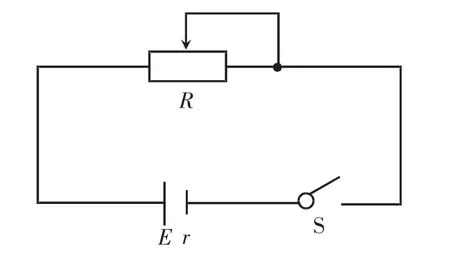
图3 变阻器与电源串联时的电路图
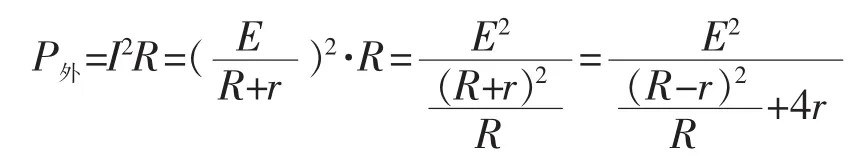
实际上,我们还可以用下面的方法得到更为一般的结论。
对任意电路,电源的输出功率均有
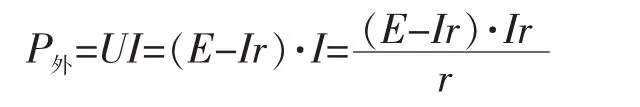
从数学角度来看,这是一个P外关于干路电流I的函数表达式,我们可以用数学均值不等式来求出电源输出功率的最大值。
(1)对任意电路:
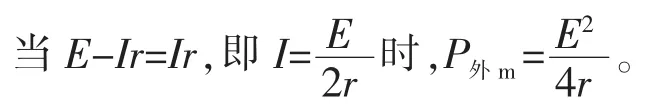
(2)纯电阻电路:
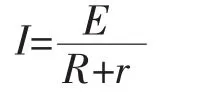
当R=r时,电源输出功率最大。
实际应用中,只需求解外电路中一部分变化电阻功率的最大值时,我们同样可以结合上面的推导来分析。
2.2 变阻器和定值电阻串联时的最大功率
如图4所示,我们需要求解滑动变阻器R的最大功率,不能直接用图3所得结论,我们可以用等效电源法来处理。如图4中的虚线所示,电源和R0串联组成等效电源,等效电动势E'=E,等效内阻r'=R0+r,此时滑动变阻器为等效电源的外电路,则可直接用图3所得电源的最大输出功率结论。
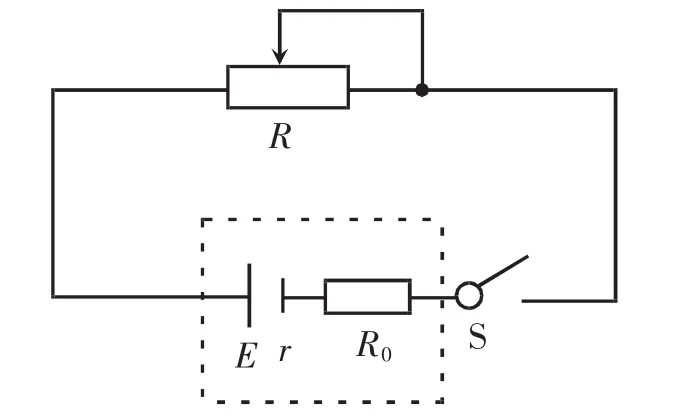
图4 变阻器与定值电阻串联时的电路图
当R=r'=R0+r时,滑动变阻器最大功率为

2.3 变阻器和定值电阻并联时的最大功率
如图5所示,当滑动变阻器和一定值电阻并联时,求解滑动变阻器的最大功率问题将变得较为复杂。若用常规解析法处理,会出现较为复杂的数学运算问题,其求解思路如下:

图5 电路图

通过上面的分析我们可以看出,常规解法往往需要用到复杂的数学运算,对于数学能力要求较高。特别是前述2.3中当滑动变阻器与定值电阻并联时涉及到的数学问题计算尤为复杂,还需要用到均值不等式的思路才能得到最后结果,对于数学基础较为薄弱的学生有很大的难度。
而等效电源法思路简单,计算容易,不易出错,学生在解题的时候所花时间也很少,相比于常规解法而言,等效电源法具有很大的优越性。
3 实验测量电源的电动势和内阻中的误差分析
3.1 实验电路中的两种连接方式
误差分析对于电路实验而言既是重点也是难点所在。由于电表内阻不能忽略,在测量电源的电动势和内阻的实验中存在不可避免的系统误差。在实验中,我们通常有两种电路连接方式,相对于待测电源而言,图6为电流表外接,图7为电流表内接。不管采用哪种连接方式,若不考虑电表内阻,改变滑动变阻器阻值,只要得到两组U、I值,都可以求出电源电动势和内阻的测量值。
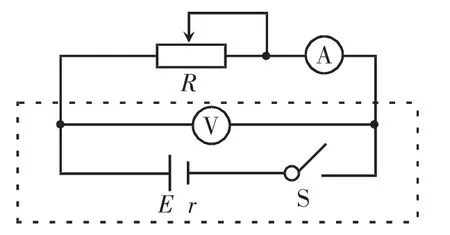
图6 电流表外接电路图
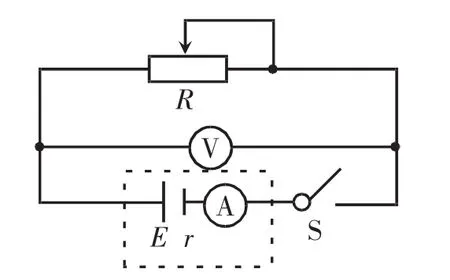
图7 电流表内接电路图
通常我们可以用解析法或者图像法对这两种电路连接方式进行结果的误差分析,均可以得出下面结论:
(1)在图6中,由于电压表分流,电动势和内阻的测量值均小于真实值,即 E测 (2)在图7中,由于电流表分压,内阻的测量值大于真实值,即 E测=E真,r测>r真。 常规解析法对于数学计算能力要求较高,数学运算复杂,容易出错。相比于常规法而言,图像法较为简单,但学生在理解图像中的两个特殊点时对实际电路经常提出下面两点疑问。(图8甲是电流表外接时电源的U-I图像,图8乙是电流表内接时电源的U-I图像。) 图8 电源U-I图 疑问1图8甲中的A点U=0,则外电路应为短路,外电阻阻值应该为零,但此时外电路为电流表和滑动变阻器串联。即使滑动变阻器阻值调为零,电流表电阻也不能忽略,所以外电路电阻不可能为零,所以外电路不可能短路。 疑问2图8乙中的B点I=0,则外电路应为断路,外电阻阻值应该为无穷大,但此时外电路为电压表和滑动变阻器并联。不管怎么调节滑动变阻器阻值,即使滑动变阻器阻值调为无穷大,电压表电阻也不能忽略,所以外电阻阻值不可能为无穷大,所以外电路不可能断路。 老师在回答此类问题时一般解释为这两种情况属于理想情况,可以有但实际实验中不能达到。这样解释从理论上可行,但因为这是属于实验中的误差分析,难免有点牵强,学生理解起来有一定难度。 下面我们用等效电源法[2]来处理此类误差分析问题。 如图6中的虚线所示,电源和电压表并联组成等效电源,则可以不考虑电压表分流。但实验所得测量值应为等效电源的等效值,即实验所得测量值应为等效电源的等效电动势E'和等效内阻r'。 如图7中的虚线所示,电源和电流表串联组成等效电源,则可以不考虑电流表分压。但实验所得测量值应为等效电源的等效值,即实验所得测量值应为等效电源的等效电动势E'和等效内阻r'。 由前面分析易得:E测=E'=E真,r测=r'=RA+r真。同样易得出结论:E测=E真,r测>r真。 通过对3.2与3.3中两种连接方式的误差分析,我们可以得出这样的结论:当电源内阻较小时,若采用电流表内接,由于RA与r真接近,因此虽然电动势测量值不存在系统误差,但是内阻测量值的相对误差很大;而若采用电流表外接,由于RV>>r真,虽然电动势和内阻测量值均存在系统误差,但是相对误差较小,所以我们在实际测量干电池的电动势和内阻时,通常采用图6的电路连接方法。但如果待测电源内阻较大,RA< 通过上面的分析可知,我们在用等效电源法分析时既避免了复杂的数学运算,又避免了图像法分析问题时带给学生的困惑,很好地解释了该实验中的误差分析问题,学生理解起来更为容易。 通过对滑动变阻器最大功率的求解及电源电动势和内阻实验中的误差分析,我们可以看出,在分析电路中某些较为复杂的问题时,相比于其他解法,等效电源法显得更为简单,可以有效地帮助学生理解和思考问题,解题思路更为清晰。因此,掌握等效电源的两种常见形式,并合理运用到电路问题分析中去,往往可以把电路中的复杂问题简单化,使电路中的数学问题变得简单。让学生可以充分利用物理的思维来解决电路问题,而不是一味地追求数学上的难度,这也是物理教学中的基本观点,使数学问题物理化。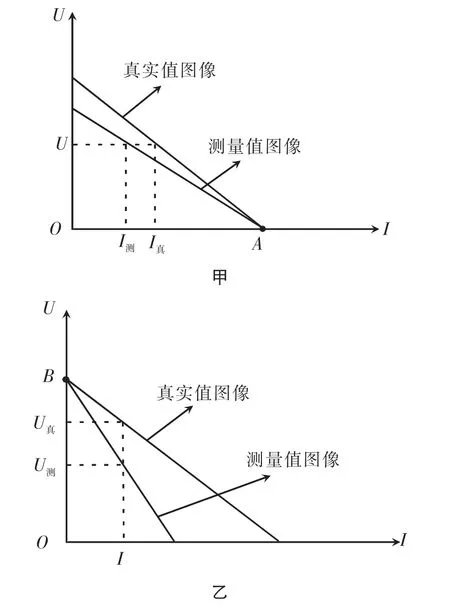
3.2 电流表外接时误差分析
3.3 电流表内接时误差分析
4 结束语

