低畸变离轴三反光学系统设计

王欣，王春艳，孙昊，刘欢，赵义武

（长春理工大学 光电工程学院，长春 130022）

星模拟器对航空、航天技术的发展起着至关重要的作用，目前正朝着长焦距、大口径、宽光谱、轻量化方向发展。由于星模拟器要模拟几光年甚至更远星体目标，因此对光学系统设计提出了更高的要求。为精确地校正航天器的姿态，要求星模拟器工作在宽光谱波段的同时可以模拟多星[1]。美国 McDonnell Douglas Aerospace研制的折射式星模拟器可模拟约50个星点，最大视场为 25°× 25°，单星张角精度优于 100″；中国科学院长春光学精密机械与物理研究应用光学国家重点实验室研制的小型星模拟器，可模拟2～8等星，视场为10.5°×7.5°，单星张角优于40″；哈尔滨工业大学超精密光电仪器工程研究所研制的星模拟器采用改进的卡塞格林系统，可模拟 0～5 等星，视场为 28'，准直性优于±120″[2]。

离轴反射式光学系统由于无中心遮拦、工作波段宽、无色差等优点可应用于星模拟器设计中，但由于反射镜优化变量少，离轴式光学系统像差不易控制。因此借助自由曲面良好的面型表征能力和平衡非对称像差的优势，使离轴反射式大视场、低畸变的光学系统设计成为可能。

1 光学系统设计理论

1.1 初始结构求解方法

离轴反射式系统通常求解方式是将共轴光学系统添加孔径偏心量和视场倾斜角，来获得理想的离轴反射式系统初始结构。对于同轴系统，三阶像差表达式为：

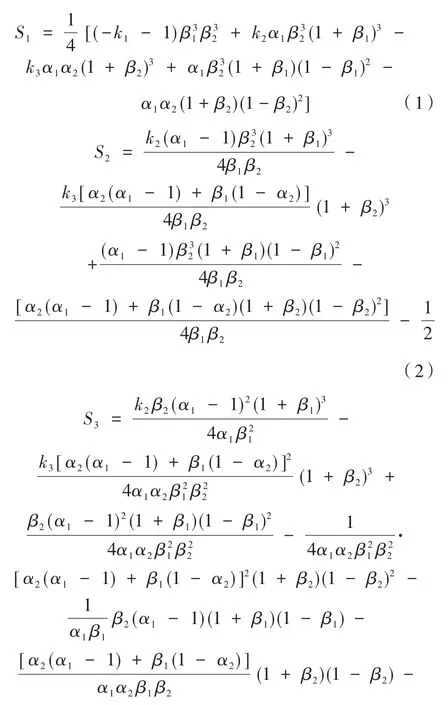
式中，S1、S2、S3分别为球差、彗差、像散；-ki表示第i面反射镜的二次锥面系数；α1、α2分别为次镜对主镜遮拦比和三镜对次镜遮拦比；β1、β2为次镜及三镜的垂轴放大率[3]。

选择无过渡像面的成像形式时，要求次镜对主镜的遮拦比α1＞0，三镜对次镜的遮拦比α2＞0，次镜的垂轴放大率β1＜0，三镜的垂轴放大率β2＜0，系统焦距f'＞0，同时反射式系统要求场曲S4=0[4]。在满足无过渡像面的情况下，求解α1、α2、β1、β2使得S1、S2、S3数值较小，且间隔合理。通过分析计算最终选择的初始结构数据为：α1=0.6，α2=0.4，β1=-1.4，β2=-0.5，此处取k1=-1，令S1=0，S2=0，计算可得k2=0.4，k3=-5，其三阶像差分别为：S1=0，S2=0，S3=0，同轴初始结构如图1（a）所示，求解的初始结构具有很好的成像质量，利于后期离轴系统的进一步优化设计。对得到的同轴初始结构添加边缘视场并进行离轴化处理，由于系统要求箱体宽小于780 mm，故光学系统的设计应尽量紧凑，设主镜的孔径偏心量为-300 mm，离轴角-3°，可满足系统要求，得到的离轴初始结构如图1（b）所示。

图1 初始结构

1.2 矢量像差理论

对于非旋转对称系统，同轴像差理论不再适用，因此引入了矢量像差理论用于对离轴光学系统的分析设计。矢量波像差是由各个表面因视场离轴所引起的像差贡献之和，当每个表面的偏心量及离轴量确定之后，系统的波像差也随之确定[5]。

则由主镜倾斜及偏心所引起的波像差为：

式中，第一项至第五项分别表示球差、彗差、像散、场曲及畸变；H表示归一化的视场矢量；ρ表示归一化的光瞳矢量[6]。

由于所设计的离轴初始结构引入了轴外视场，因此对式（4）分别分析轴上及轴外视场所引起的波像差变化，即W=W040-1(ρ·ρ)2+W0+W1，其中：

式中，W0和W1分别代表轴上视场分量及轴外视场分量在系统波像差中所做的贡献。分析式（6）可知，球差不受视场离轴影响，其余均受离轴影响较大，经ZEMAX仿真模拟，其数值分别为：S1=0，S2=-0.002 15，S3=0.000 34，S4=-0.007 48。

2 设计实例与像质分析

2.1 系统性能及指标

畸变对光学系统的成像清晰度没有影响，但它会直接影响星点的位置精度，因此消除系统畸变是设计的重点。根据畸变定义有：

为保证系统的成像位置精度，要求畸变值小于0.005 6%，模拟星等的范围为0～6星等，计算可得光源的对比度为 250∶1[7-8]，故本课题考虑选择像素大小为0.026 mm，型号为LCX023CMT的液晶光阀作为光源，其画幅尺寸为27.3 mm×21.3 mm，系统指标如表1所示。

表1 光学系统设计指标

2.2 设计结果

由于传统面型对于该指标实现较为困难，因此在所获得的初始结构中添加自由曲面，由于Zernike多项式在单位圆上的正交性，在对其各项单独进行优化时互不影响，故次镜选用Zernike多项式来平衡系统的像差；三镜采用XY多项式描述的自由曲面，选取六阶以下的项数进行优化，各项数均有选择，以此来保证弥散斑的对称性及圆整型[9]。

最终设计的结构形式如图2所示，主镜y方向倾斜角度为-5.1°，同时y方向的偏心距离为-190 mm，三镜y方向倾斜角度为3.8°，总长为649 mm，整体高度为335 mm，宽度为164 mm，最终设计的光学系统有很好的成像质量，光能损失小，边缘视场畸变小，设计上的孔径光阑位于主镜左侧500 mm处，孔径光阑由于要与星敏感器入瞳严格衔接，以免造成光能的损失，因此将孔径光阑置于主镜左侧较远位置，后根据该距离定制箱体，箱体尺寸为900 mm×600 mm×500 mm，系统结构参数如表2所示。

图2 系统结构图

表2 系统结构参数表

在所设计的光学系统中，次镜采用Zernike多项式所描述的自由曲面，参数如表3所示，三镜采用XY多项式所描述的自由曲面，参数如表4所示，面型图如图3、图4所示，次镜口径为Φ79 mm，表面矢高差为14.5 mm，三镜口径为Φ137 mm，表面矢高差为5.38 mm，可在MTC410单点金刚石车床上实现加工，采用基于单点金刚石车削技术的三轴联动加工方法，采用该方法已实现Φ682 mm口径、220 mm矢高的凹面反射镜的加工。

图3 次镜Zernike自由曲面的面型

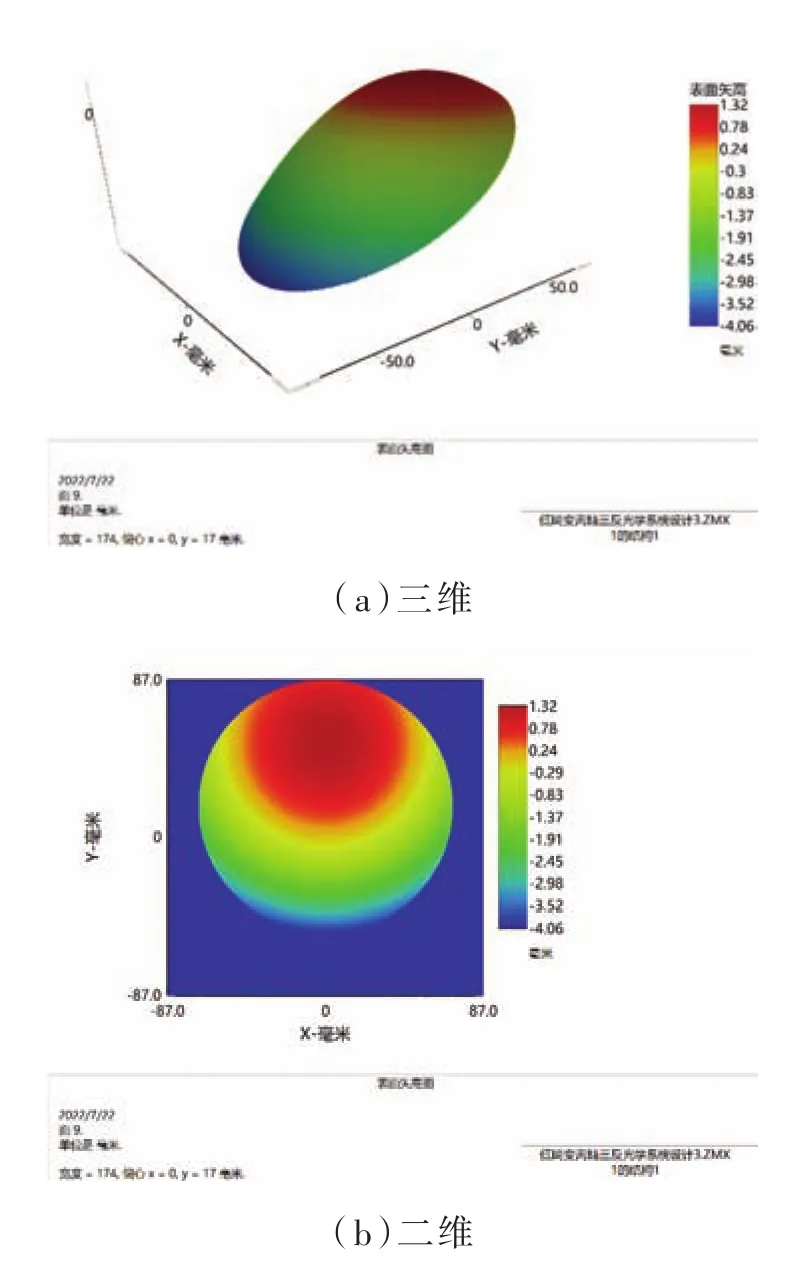
图4 三镜XY自由曲面的面型

表3 次镜Zernike多项式参数

表4 三镜XY多项式参数

主镜、次镜及三镜口径均属于小口径反射镜，根据反射镜的结构特点，选用背部中心支撑方式，可满足装调需求。

2.3 系统成像质量分析

光学传递函数是对光学系统成像质量的最综合评价，它能直接地反应光学系统的性能[10]。选用像素大小为0.026 mm的液晶光阀作为光源置于像面处，故求得奈奎斯特频率为：

由于离轴反射式系统失去了旋转对称性，故分别在+y、-y、+x、-x采样，分析图5（a）～图5（d）可知：最大畸变值为0.001 1%，优于0.005 6%；MTF曲线在19 lp/mm处均优于0.75，且接近衍射极限；质心点列图表明能量中心与主光线偏差不大，设计的光学系统最大弥散斑半径为0.458µm，弥散斑半径均小于艾里斑且光斑较为圆整；最大波前差为0.005 2λ，优于λ 10，此结果表明该光学系统具有良好的成像质量。

图5 光学系统像质评价图

3 结论

为克服反射式光学系统因增大视场所带来的像质缺陷，本文基于矢量像差理论分析了视场及视场离轴所引起的像质变化，构建了基于自由曲面的像差校正模型。根据矢量像差理论所分析的结果，利用自由曲面的面型特征，有针对性地选取Zernike多项式的项数及XY多项式的阶数，设计了含有自由曲面的大视场低畸变离轴三反光学系统。设计结果表明，在离轴反射式系统中引入不同形式的自由曲面，在一定程度上改善了各个视场的像质，并通过优化达到了预期的畸变要求。所设计的光学系统在2.4°的视场范围内，所达成的像质较好，可用于高精度的星敏感器的标定。本次设计仅限于对复杂面型的应用研究，后续将从复杂面型的检测技术研究展开。