Stewart六自由度并联机构位姿分辨率分析方法

梁凤超，赵筱琳，谭爽，范建凯，林喆，石志成

（北京空间机电研究所，北京 100090）

近年来，空间光学遥感器分辨率需求越来越高，使得超长焦距、超大口径空间光学遥感器成为重要研究方向之一。受镜面加工能力及火箭运载能力的限制，超大口径空间遥感器主镜通常采取分块拼接的方式[1-2]。而在轨展开机构拼接主镜精度有限，需高分辨率位姿调整机构对分块镜群及次镜的位姿实施在轨校正，以满足超大口径空间望远镜高分辨率成像的要求。即使对于主镜未采取分块拼接方式的光学遥感器，相机入轨后力热环境变化也会导致主次镜空间位姿发生改变，同样需要高分辨率位姿调整机构在轨调整次镜位姿[3-4]。而完成主镜分块镜及次镜位姿精密调整的关键是六自由度并联机构，该机构的位姿分辨率是影响分块镜及次镜位姿调整的关键。空间光学遥感器地面光学装调及光学像差在轨主动校正亟需研制高分辨率六自由度并联机构。

研制高分辨率六自由度并联机构不能也不必在其位姿分辨率参数还不明确的情况下制造实体机构，因为这是成本极高且很难收到良好效果的。因此，需要一种分析方法，实现在设计阶段分析六自由度并联机构位姿分辨率，确保其关键性能满足使用要求。针对此需求，本文提出一种基于驱动支链实际分辨率的位姿分辨率分析方法，为研制高分辨率Stewart六自由度并联机构提供有力的分析保障。

1 运动学建模

典型的Stewart构型6-UCU（U-虎克铰副，C-圆柱副）六自由度并联机构组成及坐标系定义如图1、图2所示。六自由度并联机构由上下两个平台和6个并联的、可独立自由伸缩的驱动支链组成，驱动支链和平台之间通过虎克铰A1、A2、A3、A4、A5、A6和虎克铰B1、B2、B3、B4、B5、B6连接。将下平台作为基础平台（定平台），以驱动支链的伸缩位移作为输入变量，则可以控制上平台（动平台）的空间位移和姿态。如图2所示，六自由度并联机构的结构参数有r-动平台铰点圆半径，R-静平台铰点圆半径、α-动平台铰点短边圆心角一半、β-静平台铰点短边圆心角一半和H-并联机构中位时p与O的距离，确定上述五个参数，就可以完全描述Stewart六自由度并联机构的基本结构。

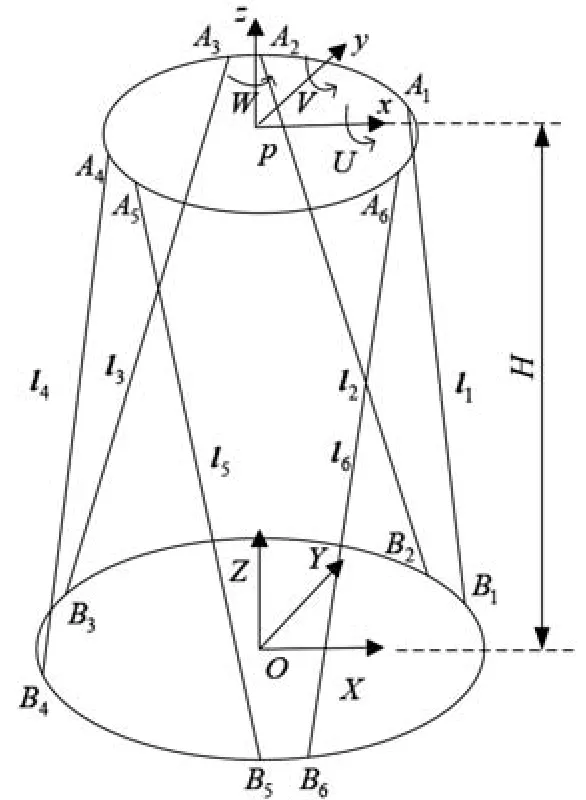
图1 典型Stewart

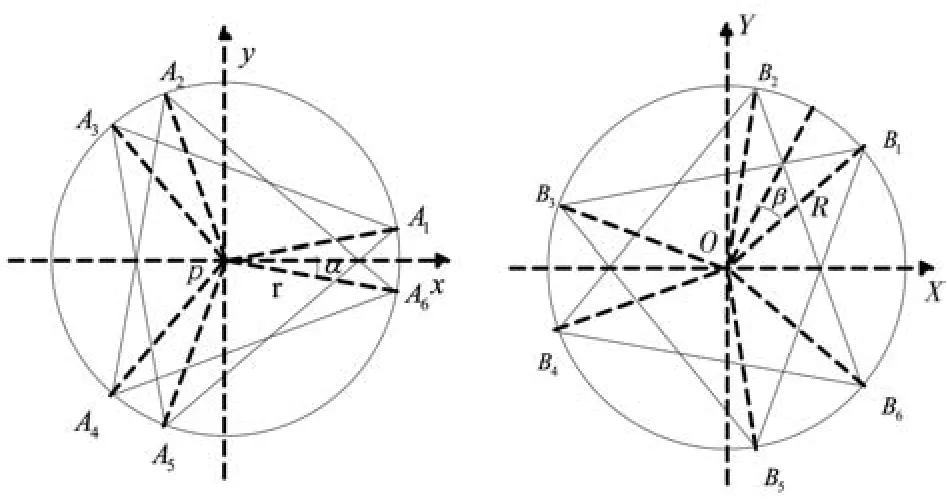
图2 上下平台铰点分布

1.1 运动学逆解数学模型

如图1、图2所示，为了建立Stewart六自由度并联机构运动学数学模型[5-10]，在静平台铰点所在圆的圆心处建立静坐标系O-XYZ，坐标原点为O；在动平台铰点所在圆的圆心处建立动坐标系p-xyz，坐标原点为p。坐标系确定之后，六自由度并联机构的运动平台的位姿用广义坐标向量q表示，其中q=[x y z U V W]T，[x y z]T表示p作为旋转中心时，点p在静坐标系中的坐标向量，[U V W]T表示p-xyz在静坐标系中的姿态角。这六个参数就确定了动平台的空间位姿。旋转变换矩阵可将动平台各点坐标统一在静坐标系中，根据动平台目标位姿计算出驱动支链位置（运动学逆解）或根据支链位置求出当前动平台位姿（运动学正解）。旋转变换矩阵表达式如下[11-13]：

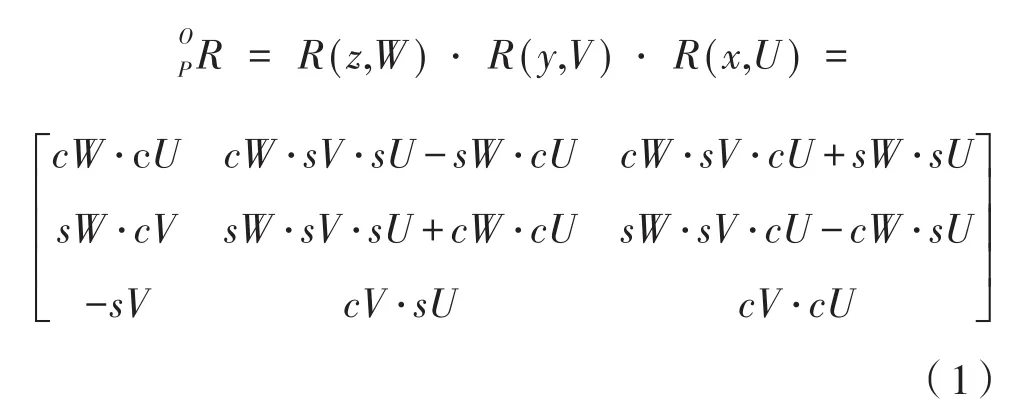
其中，cU=cos（U），cV=cos（V），cW=cos（W）；sU=sin（U）；sV=sin（V）；sW=sin（W）。动平台姿态广义坐标向量q=[x y z U V W]T时，各驱动支链的长度如下：

其中，矢量Li为图1所示的支链矢量AiBi；li为支链长度，i=1，2，…，6，i表示驱动支链的序号。至此，建立了并联机构运动学逆解数学模型。

1.2 运动学正解数学模型

目前并联机构的正解主要有数值法[14-15]和解析法[16-17]。数值法就是给定一个初值，从这个初值开始通过循环、迭代直到获得满足给定精度要求的解。数值法数学模型简单，可以求解任何并联机构。下面应用Newton-Raphson法建立六自由度并联机构运动学正解数值解模型。定义下面的目标向量函数f来描述驱动支链伸缩长度的估计值li与实测值|Li|之间的不同，即：

式中，li表示估计位姿对应的6个驱动支链伸缩长度的估计值；|Li|表示6个驱动支链伸缩长度的实测值；f1…f6分别表示li的平方与实测值|Li|的平方之间的偏差。

Newton-Raphson法以目标向量函数f取极小值为目标，求解六自由度并联机构位姿数组Q的步骤如下：

（1）测量6个驱动支链的坐标向量Li，计算驱动支链伸缩长度的实测值|Li|；

（2）选取运动平台的位姿初值Q，该位姿初值Q，利用逆解公式计算各支链伸缩长度估计值li；

（3）基于6个驱动支链伸缩长度的实测值和估计值li，构成数组函数f；

（4）计算雅克比矩阵；

（5）利用JδQ=-f计算位姿修正值δQ；

（6）如果δQTδQ＜ε（ε为位姿误差阈值）成立，则Q为所求的位姿，否则，进行下一步；

（7）计算Q=Q+δQ，并转到步骤（2）。

步骤（4）中雅克比矩阵的计算公式如下：

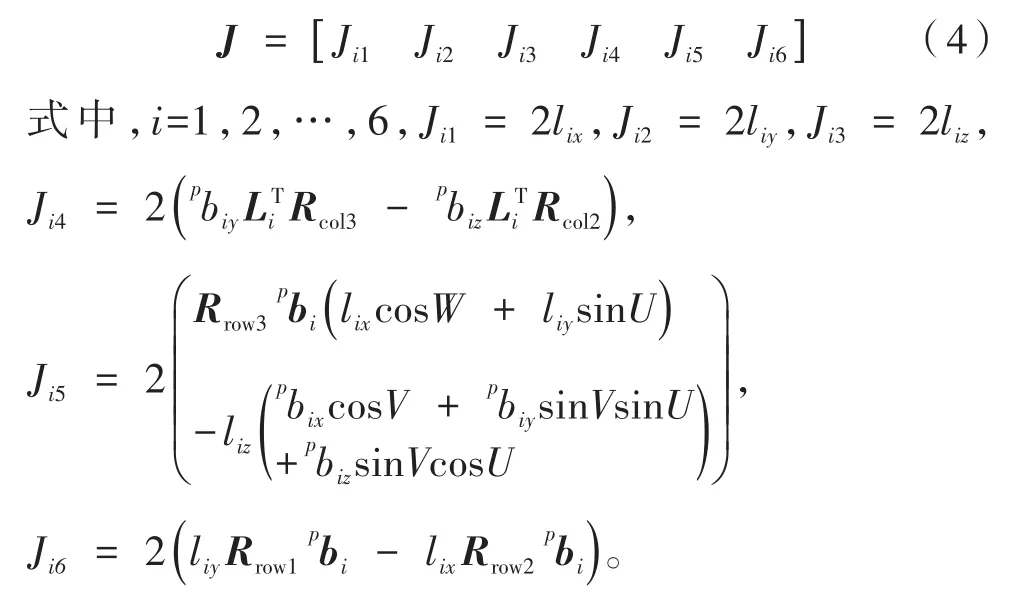
Li=[lixliyliz]T为第i个驱动支链的坐标向量；为动平台上第i个驱动支链对应的铰点在动坐标系p-xyz坐标系下的坐标向量；Rcol2、Rcol3分别表示旋转变换矩阵R的第2、3 列；Rrow1、Rrow2、Rrow3分别表示R的第 1、2、3行。

2 位姿分辨率分析方法

位移分辨率是给定指令后机构的最小运动增量，包括设计分辨率与实际分辨率。例如脉冲当量即为设计分辨率。但在实际应用中，由于间隙、形变等因素的影响，机构很难具有脉冲当量那么小的运动增量，实际运动分辨率会是脉冲当量数倍甚至数十倍，且只能由实测得到。

2.1 位姿分辨率

六自由度并联机构位姿分辨率是六个单自由度的最小运动增量[18]：即3个平移分辨率Δx、Δy、Δz和 3个绕x、y、z轴的转角分辨率 ΔU、ΔV、ΔW。

常规笛卡尔坐标运动机构每个驱动轴对应一个自由度，控制方式是独立控制每个驱动支链来控制该自由度的运动。虽然六自由度并联机构位姿分辨率指标是以笛卡儿坐标系形式表达的，但是六自由度并联机构是非线性、强耦合的多输入多输出系统：并联机构的一个输入即任一驱动支链伸缩，会影响所有输出，任一自由度输出由所有输入即驱动支链伸缩量来决定。想要得到单自由度运动分辨率，必须通过计算得到特定的控制指令，控制六个驱动支链运动，实现仅在指定的单自由度输出最小运动增量，而其他五个自由度输出为零或者可忽略的耦合运动量。该指定自由度的最小运动增量即为该自由度的运动分辨率。可见，分析六自由度并联机构位姿分辨率的关键之一就是求得动平台的单自由度运动指令，即求得一组驱动支链增量数组，按该数组驱动六支链即可实现动平台的单自由度最小运动。

另外，在分析六自由度并联机构的分辨率时，不能以支链理论计算脉冲当量去分析，而需考虑支链的实际分辨率，这样得到的分辨率更接近工程实际。

2.2 位姿分辨率分析方法

六自由度并联机构位姿分辨率分析方法如图3所示，以运动逆解、正解数学模型为基础、利用支链增量缩放不改变单自由度运动的特性、以驱动支链实际分辨率为量化基准，通过目标位姿计算目标支链增量，再对目标支链增量量化、寻找最小量化倍数绝对值，得到最小支链增量数组、支链长度，进而应用正解数学模型求出六自由度并联机构位姿分辨率。该分析方法具体步骤如下：

图3 六自由度并联机构位姿分辨率分析方法

（1）建立运动学模型

建立公式（1）～公式（4）所示的六自由度并联机构的运动学逆解、正解模型。

（2）初始化参数

初始化如下参数：结构参数r、R、α、β、H，支链实际分辨率FBL，目标位姿系数n（n一般取10～20），初始位姿q1=[x1y1z1U1V1W1]T，自由度序号j。

（3）计算q1对应的支链长度数组L1

调用运动学逆解模型，计算q1对应的支链长度L1=[l1l2l3l4l5l6]T。

（4）给定目标位姿

（5）计算支链长度增量数组

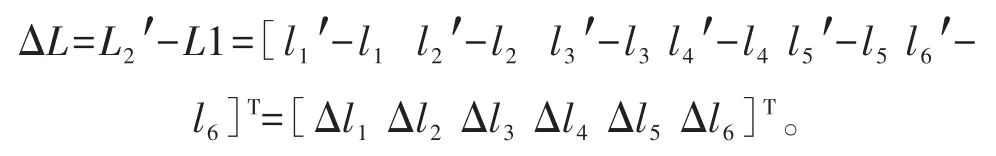
（6）ΔL按支链分辨率量化。

量化的意义在于得到各个支链的实际可达运动增量。ΔL按支链实际分辨率量化得到量化支链增量数组qΔL：

qΔL=[qΔl1qΔl2qΔl3qΔl4qΔl5qΔl6]T，量化的算法为：qΔli=Mi×FBL，Mi=int（Δli/FBL）。Mi为 ΔL相对于支链分辨率的量化倍数，int（）表示取整运算。

此时，将qΔL作为增量施加到各支链时，并联机构会输出步骤（4）中给定的单自由度运动，但因qΔL不是最小支链增量数组，该单自由度运动增量不是分辨率。由于对于同一个结构参数的并联机构，在对其进行单自由度驱动时，支链长度增量数组同时放大或缩小正数倍（仅缩放、不改变方向）时，机构仍保持原指令的单自由度运动。下一步要求出这个最小的正数倍Mmin，将qΔL数值除以Mmin，就得到该自由度分辨率指令，即最小驱动增量数组qminΔL。

（7）计算最小倍数绝对值Mmin

Mmin是计算单自由度分辨率指令即最小驱动增量数组的关键。如果支链理论增量Δli＜FBL，则量化倍数Mi=int（Δli/FBL）=0，进而量化值qΔli=Mi×FBL=0。确定Mmin要去掉为 0 的Mi，得到新的一组Mk∈Mi，Mk≠ 0，k=1，2，…，n，k≤6；然后，找出非零Mk绝对值的最小值Mmin：Mmin=Min（abs（Mk））；其中，abs（Mk）得到量化倍数的绝对值，abs（）是取绝对值运算；Min（abs（Mk））得到Mk的最小值绝对值，Min（）为取最小值运算。

（8）计算单自由度分辨率指令

将qΔL=[qΔl1qΔl2qΔl3qΔl4qΔl5qΔl6]T除以Mmin，即可得到该自由度分辨率指令：最小驱动增量数组qminΔL。

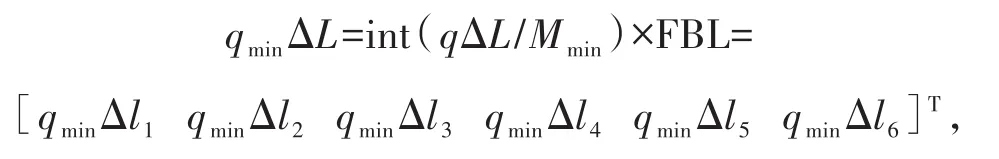
其中，qminΔli=int（qΔli/Mmin）×FBL。

（9）计算分辨率位姿q2

单自由度分辨率指令的支链长度数组为：

L2=L1+qminΔL=[l1+qminΔl1l2+qminΔl2l3+qminΔl3l4+qminΔl4l5+qminΔl5l6+qminΔl6]T。 然后 调用 正解数学模型，计算L2对应的位姿q2：q2=[x2y2z2U2V2W2]T。

（10）计算单自由度分辨率

分辨率位姿q2与初始位姿q1相减，得到该自由度分辨率：

当j=1时，得到x自由度分辨率Δx，Δqx=q2-q1；同理，j=2～6 时，分别得到 Δy、Δz、ΔU、ΔV、ΔW。

可根据需要，从步骤（2）开始，重新输入六自由度并联机构的结构参数与支链分辨率，进行新一轮分辨率分析。

3 分辨率分析及测试

3.1 分辨率分析

某空间相机次镜口径0.5 m，重25 kg，需研制高分辨率次镜Stewart平台，实现相机地面光学装调及在轨像差主动校正模拟。该Stewart平台分辨率指标为Δx、Δy、Δz：0.2 µm，ΔU、ΔV、ΔW：1″。

经过六自由度并联机构的参数化建模、运动学动力学分析、结构优化设计，得到六自由度并联机构的结构参数：r=239.51 mm、R=249 mm、α=6.589°、β=7.677 6°和H=195.03 mm。然后，须根据平台分辨率指标计算驱动支链实际分辨率需求。根据平移分辨率0.2µm、旋转分辨率1″的指标要求，在平台分别施加单自由度分辨率的运动增量，进行运动学逆解运算，可得到平台分辨率对驱动支链的分辨率需求。分析结果显示需要驱动支链分辨率优于60 nm才能实现平台的分辨率指标。该平台采用的驱动支链及其分辨率如图4所示，其理论分辨率即脉冲当量为5 nm，实际分辨率为50 nm，满足驱动支链优于60 nm的需求。

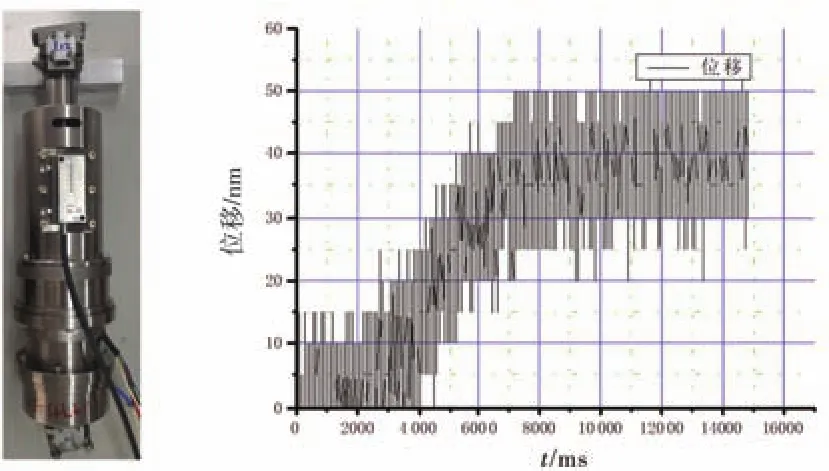
图4 驱动支链位移分辨率达到50 nm

接下来，须基于结构参数及驱动支链实际分辨率，分析Stewart平台的分辨率。由于六个自由度分辨率分析过程类似，下面仅以平移x方向分辨率为例，介绍一下分析过程。

首先，根据结构参数，计算上下铰点Ai、Bi的空间坐标、旋转矩阵R，得到运动学数学模型。由于初始位姿的选取不影响分析结果，取初始位姿q1为零位位姿。然后，调用运动学逆解模块，计算q1对应的杆长数组：L1=[272.301 812 272.301 812 272.301 812 272.301 812 272.301 812]T。之后，取n=10，则x方向目标位移增量为x=n×FBL=10×50 nm=0.000 5 mm。给定目标位姿qx=[0.000 5 0 0 0 0 0]T。接着调用运动学逆解模块，计算得到qx对应的杆长数组。L2'=[272.301 862 272.301 712 272.301 862 272.301 862 272.301 712 272.301 862]T。则支链长度增量数组ΔL=L2'-L1=[0.000 157-0.000 348 0.000 191 0.000 191 -0.000 348 0.000 157]T。之后，ΔL按支链分辨率量化后得到qΔL=[0.000 15-0.000 3 0.000 15 0.000 15 -0.000 3 0.000 15]T，但因qΔL不是最小支链增量数组，由qΔL作为输入得到的x方向运动增量不是分辨率。必须计算qΔL的最小倍数绝对值，进行等比例缩小，得到最小支链增量数组、支链长度数组。

经计算得到最小倍数绝对值Mmin=3。将qΔL等比例缩小3倍即可得到x自由度分辨率指令。qminΔL=[0.000 05 -0.000 1 0.000 05 0.000 05-0.000 1 0.000 05]T。此即分辨率位姿q2的驱动支链增量数组。而此时q2对应的单自由度分辨率指令的支链长度数组为：L2=L1+qΔL=[272.301 812 272.301 812 272.301 812 272.301 812 272.301 812]T。此时，调用正解数学模型，计算L2对应的分辨率位姿q2：q2=[0.166 7 0 0 0 -0.000 112 0]T。而 Δqx=q2-q1=[0.166 7 0 0 0 -0.000 112 0]T，则x自由度的分辨率为Δx=0.166 7 mm，绕x方向上有-0.000 112″的耦合量，与1″的指标相比可以忽略。

应用基于VC++开发了六自由度并联机构位姿分辨率分析软件，分辨率分析算法及工作流程如图3所示，软件界面如图5所示。经计算，得到该Stewart平台的分辨率分别为：Δx=0.17µm，Δy=0.15 µm，Δz=0.14 µm，ΔU=0.77″、ΔV=0.74″、ΔW=0.75″。部分中间结果如“支链增量（µm）”“增量量化（µm）”“最小驱动量（mm）”会显示出来，最后会显示分析结果：分辨率（µm/″）。理论分析结果表明：该Stewart平台平移分辨率优于0.2 µm，转角分辨率优于1″。

图5 位姿分辨率分析软件

3.2 分辨率测试

研制的Stewart次镜并联机构如图6所示。该并联机构的位移及转角分辨率是实现次镜位姿精密调整的关键，这就需要建立六自由度位姿测量系统，对该并联机构的位姿调整分辨率及调整范围进行测试。

图6 Stewart并联平台

Stewart次镜并联机构平移及转角分辨率测试系统如图7所示。系统由RENISHAW XL-80双频激光干涉仪、AUTOMAT自准直仪、Stewart次镜平台及模拟负载、并联机构控制器组成。双频激光干涉仪用于平移分辨率测试，自准直仪用于转角分辨率测试。整个测试系统搭建在恒温实验室内隔振光学平台上，可有效防止温漂引起的形变误差、隔离和衰减低频、高频振动。该测试系统平移测量分辨率达到1 nm、角度测量分辨率达到0.002″。

图7 Stewart并联机构分辨率测试系统

平台分辨率测试采用六个自由度分开测试的方法，每个自由度都是先以技术要求指标5倍的步距步进，停留约20 s，使设备稳定下来，再步进，前进5步后，再后退5步。然后依此步骤逐步降低指令值，例如x方向分辨率测试，分别x平移1µm、0.8µm、0.6µm、0.4µm、0.2µm、0.1µm的平移指令，激光干涉仪测试曲线能够很好分辨出x平移0.2～1µm的指令，而继续尝试给出更小的平移指令0.1µm时，测得位移曲线台阶不明显，故判定平台的x平移自由度分辨率为0.2µm。x平移自由度实测分辨率如图8所示。同理测得平台y、z自由度的平移分辨率也为0.2µm。

图8 平移x自由度分辨率测试曲线

平台绕x轴旋转分辨率指标为1″，依次给定5″、4″、3″、2″、1″、0.5″的转角步距指令，进行分辨率测试，自准直仪测试结果表明Stewart平台很好地分辨出了 5″、4″、3″、2″、1″的转角指令；当指令值低于1″时，曲线台阶不明显，判定平台绕x轴转角分辨率为1″。绕x轴旋转U自由度分辨率测试曲线如图9所示。同理测得平台绕y轴、绕z轴旋转的分辨率均达到1″。

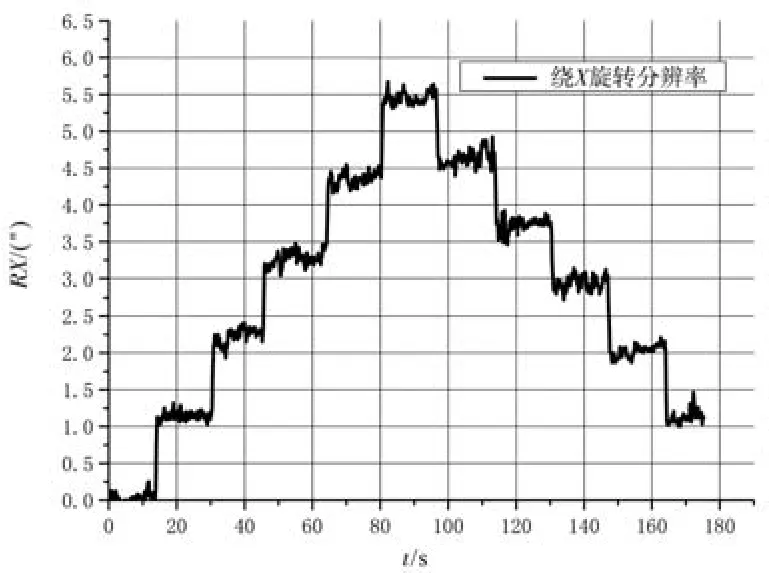
图9 绕x轴旋转U自由度分辨率测试曲线

该Stewart平台分辨率分析结果为，Δx=0.17µm，Δy=0.15 µm，Δz=0.14 µm，ΔU=0.77″，ΔV=0.74″、ΔW=0.75″。实测结果为平移 0.2 µm，旋转 1″，与理论分析结果基本一致。

4 结论

高分辨率Stewart六自由度并联机构是精密调整主镜分块镜及次镜位姿、实现空间光学遥感器光学像差主动校正的关键。为给高位姿分辨率Stewart六自由度并联机构研制提供分析保障，本文提出了一种在设计阶段分析并联机构位姿分辨率的分析方法。该方法通过建立六自由度并联机构运动模型，利用支链增量缩放不改变单自由度运动的特性，经对支链增量进行特殊量化处理，得到最小支链增量数组，进而求出位姿分辨率。

基于VC++开发了六自由度并联机构位姿分析软件，实现了不同结构参数六自由度并联机构的位姿分辨率分析。应用该软件分析了某空间相机次镜六自由度并联机构的位姿分辨率，测试结果表明，分析结果与实测结果基本一致。本分析方法成功设计了多台高分辨率六自由度并联机构，具有较强的工程指导价值。