基于SOP-SeedBS的高维数据稀疏变点检验
银炳皓,施三支,齐德全
(长春理工大学 数学与统计学院,长春 130022)
变点估计和检验问题是统计学中的一个经典问题,用于识别时间序列中的突变,发生这种突然变化的时间点称为“变点”。通过估计变点的位置,可以将原始数据集划分为较短的段,然后使用平稳时间序列的方法进行分析,解决各个领域相关的问题。变点问题在金融行业[1]、互联网安全[2]、生物医学[3]等领域都有着广泛的应用,例如,变点估计可用于发出有关异常金融事件的警报,检测网络上的分布式拒绝服务攻击,精确定位人脑中脑波活动的开始等。随着时代的发展和科技的进步,现实生活中的数据多以高维的形式出现,高维数据流导致了数据量的激增,这就要求变点分析方法能有所进步,并且在运算时间和方法准确性上达到一个良好的平衡效果。
经典的变点检验关注的是单变量时间序列,例如2012年Killick[4]提出的PELT方法是通过找到变点可能的数量和位置的成本函数最小值,来推断变点的最佳数量和位置。2014年Frick和Munk等人[5]提出的SMUCE算法针对指数族回归中的变点问题,引入了一种新的估计量;2014年Fryzlewicz[6]提出的 WBS 算法和 2018 年 Baranowski等人[7]提出的最窄超阈值法(NOT)提高了二元分割算法的性能。然而,经典的单变量变点检验方法通常不直接适用于现代应用中经常遇到的高维数据集。因此,学者们提出了几种方法来估计和检验高维数据中的变点,并且为了解决维数灾难的问题,现有的几种高维变点检验方法假设了变化信号具有某种形式的稀疏性,稀疏性假设大大降低了原始高维问题的复杂性。例如,在 2015年 Jirak[8]使用 CUSUM 统计量对不同子部分进行L∞聚合,对于稀疏变点的效果很好;2015 年 Cho 和 Fryzlowicz[9]的稀疏二元分割算法,也考虑了稀疏性;2018年Wang和Samworth[10]基于投影的方法中假设了一个变点前后的均值差异只在小部分维数坐标中是非零的;2019 年 Enikeeva和 Harchaoui[11]提出了基于具有稀疏性的扫描统计量的方法。关于高维数据的变点检验问题的工具仍在不断创新和发展,但大多不具有普适性,且运算时间较长。
本文通过研究具有稀疏变点的高维数据的特点,提出了一种基于稀疏最优投影的多变点检验方法,SOP-SeedBS方法能够检验出数据的维度p在小于或大于等于数据量n的情况下变点的位置及个数,并研究了变点间隔大小对该检验方法稳定性的影响。通过仿真模拟,在多种情况下与Wang和Samworth的Inspect方法(2018)进行了比较,结果表明,SOP-SeedBS方法具有较高的准确度,并在计算时间方面具有明显的优势。
1 SOP-SeedBS高维稀疏多变点检验
1.1 稀疏变点模型
设X1,…,Xn是n个相互独立的p维随机向量,Xt~Np(μt,σ2Ip),1 ≤t≤n,σ2是方差,记
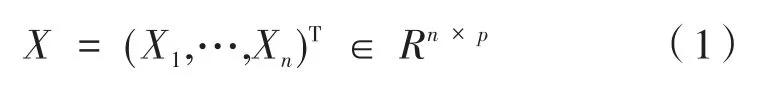
其中,p可能与序列的长度n相等,甚至大于序列的长度n。
假设存在υ个变点,变点检验的问题能被表示为经典的假设检验问题
假设备择假设成立,数据可划分成υ+1段的分段常数均值结构,换句话说,如果有υ个变点 1≤z1<z2<…<zυ,即∀0 ≤i≤υ。记z0=0,zυ+1=n, 记θ(i)=μ(i)-μ(i-1),i=1,…,υ。
本文假设均值的变化是稀疏的,即一个变点前后的均值差异只在小部分维度(p)中是非零的。记‖θ(i)‖0表示向量θ(i)中非零元素的个数,则‖θ(i)‖0≤k,k∈{1,…,p}且k≪p。本文只考虑参数μ(i)的检验问题,其他参数皆视为讨厌参数。假设变点位置z1,z2,…,zυ满足:
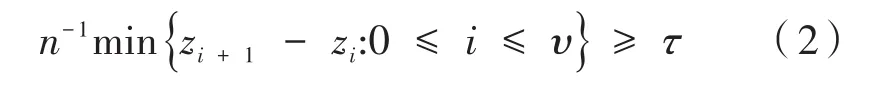
其中,τ是变点的最小间隔,0<τ<1。均值变化的大小满足:

其中,ϑ是均值变化大小的阈值。
1.2 稀疏最优投影(SOP)
Wang等人[10](2018)通过对高维数据进行高维CUSUM变换进而推导出数据矩阵的最优投影方向,并解决了计算第一个左奇异向量引出的凸优化问题。因此对于高维稀疏变点数据,本文根据类似的思想,并基于奇异值分解和凸松弛优化方法将高维数据投影成一维数据,由于本文研究的高维数据中均值变化是稀疏的,从而称该方法为稀疏最优投影(Sparse Optimal Projection)。
对于任意的a∈Rp,满足 ‖a‖2=1,其中
选择a=θ/‖θ‖2来最大限度地扩大两个数据片段之间的均值差异的大小。然而θ在实践中通常是未知的,本文的想法是寻找一个最优的投影方向v=θ/‖θ‖2,文献[10]启发了本文对数据矩阵X进行分解,再利用奇异值分解得到一个合适的投影方向后,将数据投影到一维空间。
假设均值变化只出现在数据矩阵X的k个列中,且在没有发生均值变化的p-k个列中的元素均值为μt=0,t∈{1,…,n},k∈{1,…,p} 。对数据矩阵X进行分解,得到X=μ+W,其中μ=(μ1,…,μn)T∈Rn×p是均值矩阵,W=(W1,…,Wn)T∈Rn×p,W1,…,Wn是独立的Np(0,σ2Ip)的随机噪声。当σ已知,零假设成立时,μ为恒定的常数向量,备择假设下只存在一个变点z时,矩阵X的元素均值可以计算出:
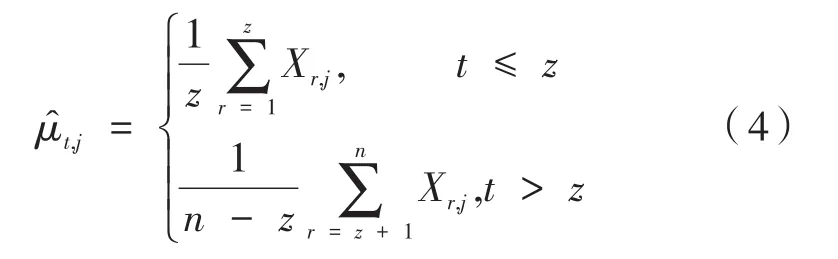
其中,Xr,j为矩阵X中第r行,第j列的元素;t∈{1,…,n} ;j∈ {1,…,p}。记前z行向量元素相同,后n-z行向量元素相同。

这里St,j为第j列中变点z前后分段数据之和,t∈{1,…,n},j∈{1,…,p} ,即:
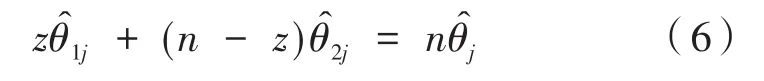
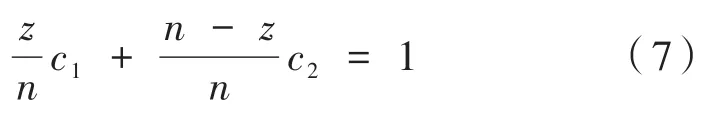
则有:

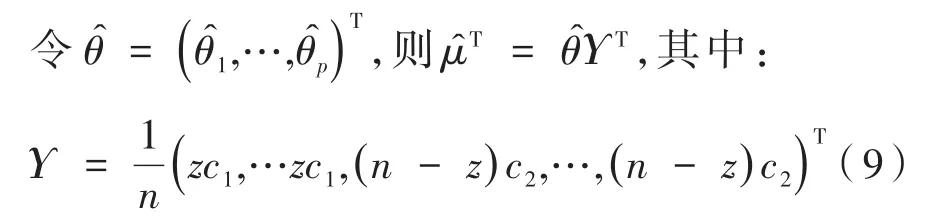
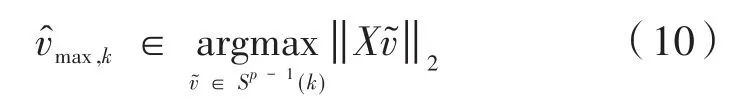
文献[10]中,计算矩阵XT的第一个左奇异向量是一个组合优化问题。公式(10)是一个计算复杂度很高的凸优化问题,解决这个问题的一种方法是使用优化问题中的凸松弛得到M̂来代替X,具体过程如下:
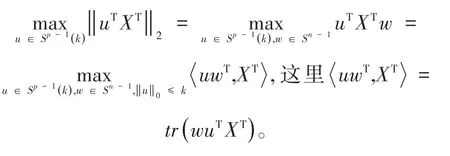
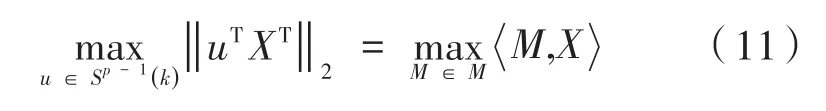
惩罚函数可以将有约束的目标函数转化为无约束的目标函数,即当得到的M不满足约束条件时,估计的̂可能会远离最优解。通过添加一个惩罚项 -λ‖M‖1,优化问题变为以下形式:
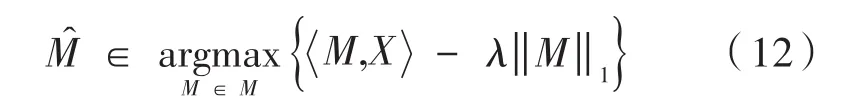
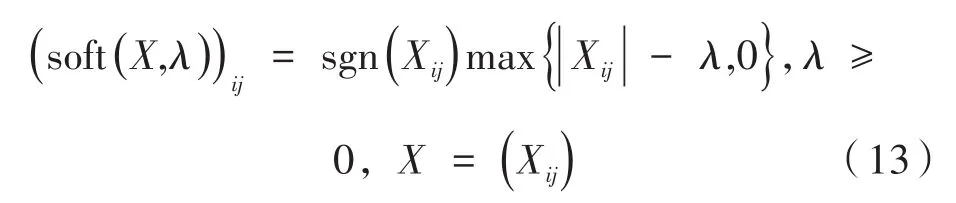
其中,λ为软阈值。则有:
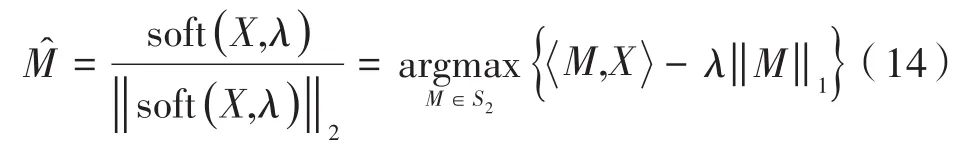
记是的第一个左奇异向量,即:
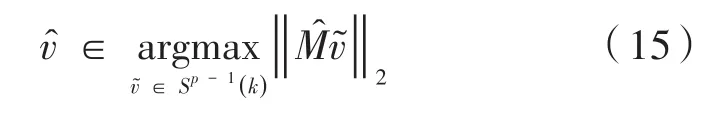
将高维数据X沿着最优方向投影,得到一维数据,记为Y。
如果数据存在变点,投影后的一维数据呈现出了分段常数的特征,适用于此种数据的几种经典的单变量多变点检验方法,包括2012年Killick[4]给 出 的 PELT 方 法 、2014 年 Fryzlewicz[6]提出的 WBS方法、2018年 Baranowski等人[7]给出的最窄超阈值方法(NOT)以及2020年Kovács等人[12]提出的SeedBS方法。PELT方法是通过找到变点可能的数量和位置的成本函数最小值来推断变点的最佳数量和位置,计算复杂度较高。WBS方法和NOT方法都是基于二元分割思想的改进算法,NOT方法中随机抽取间隔的想法与WBS方法类似,但NOT方法更关注数据中可能存在变点的最小间隔。WBS和NOT方法中用于搜索变点的间隔都是通过随机抽样构造的,在数据量较大的情况下,需要构造的随机间隔数量会很多,且会出现许多长度与原始序列相同或者重复出现的间隔,这增加了算法复杂度和运算时间,特别是高维稀疏变点数据中变点较少的情况下。2020 年 Kovács等人[12]提出的种子二元分割(SeedBS)是一种解决大规模数据变点检验问题的方法,该方法能够有效地降低计算复杂度,提高计算效率。因此,本文选择SeedBS算法来对投影后的一维数据进行多变点检验。
1.3 种子二元分割(SeedBS)
种子二元分割方法是通过构造一个具有确定性,且可以预先计算的搜索区间集来搜索变点。区间集的构造独立于潜在的变点数量,并能达到搜索间隔的总长度尽可能小的效果。
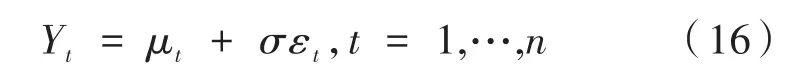
其中,μt是t时刻的信号;σ是恒定标准差;εt是正态噪声,记有υ个变点1≤z1<z2< ...<zυ,则μt可以被分为υ+1段,其中第i段中。
记a∈(1/2,1]为一个给定的衰减参数,对于任意的q:1≤q≤log1/a(n),将第q层定义为由nq个区间组成,初始长度为lq且进行确定性位移sq的集合Lq:

例如当a=1/2时,得到一个重叠的二元分隔区间。来自前一层的每个间隔都被分成左、右和重叠的中间间隔,每个间隔的大小都是前一层的一半。当间隔的长度在层上迅速衰减时,随着间隔长度变小,间隔的数量迅速增加,还保证了在同一层内的连续间隔之间有足够大的重叠。生成的间隔如图1所示[12]。

图1 a=1/2时生成搜索间隔的可视化图
用于种子二元分割的检验统计量是定义一段内分割点在s的CUSUM统计量:
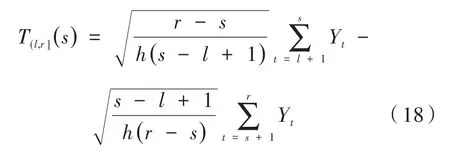
其中,0≤l<r≤n和h=r-l为整数,达到CUSUM统计量绝对值最大值的位置s记为最好的分割点。因此,计算m个种子间隔的检验统计量,得到一个候选变点集,记为,如果候选变点集合中对应间隔的检验统计量超过了阈值ζn,就认为得到一个最终的变点估计集合O(0,n],并将声明为一个变点:
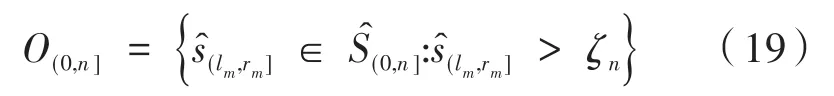
其中:

阈值ζn可以通过强化施瓦茨信息准则计算:
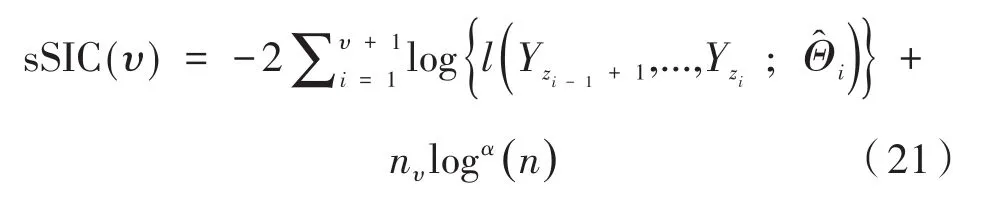
其中,α≥ 1;是模型(2)分段参数μ(i)的最大似然估计;nυ表示需要估计参数的总个数,包括变点位置。另外,当α=1时相当于施瓦茨信息准则。
在具有固定的方差σ2和分段常数均值的单变量高斯信号模型中,也可以通过贝叶斯信息准则(BIC)来计算阈值:
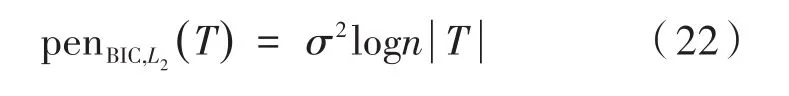
其中,σ2是方差;n为样本量;T={z1,…,zυ} ⊂ {1,…,n} ;|T|为集合T的基数。通过BIC准则计算出的阈值筛选出的变点个数要多于强化施瓦茨信息准则筛选出的变点个数。
1.4 SOP-SeedBS方法
本文结合了类似 Wang等人[10](2018)的投影思想和 Kovács等人[12](2020)提出的种子二元分割(SeedBS)方法,进行高维数据的稀疏变点检验,先将高维稀疏变点数据沿着最优的投影方向投影到一维,再利用SeedBS方法对一维数据进行多变点检验,SOP-SeedBS方法具体步骤如下:
输入:数据矩阵X=(X1,...,Xn)T∈Rn×p,软阈值λ,衰减参数足够大的变点上界K,max阈值ζn。
(1)对数据矩阵X进行分解并推导出最优投影方向。
(3)对进行SVD分解,得到第一个左奇异向量,计算投影数据
(4)根据衰减参数a构造包含m个种子区间的区间集。
(5)计算m个种子间隔的检验统计量,并根据阈值ζn确定变点位置:
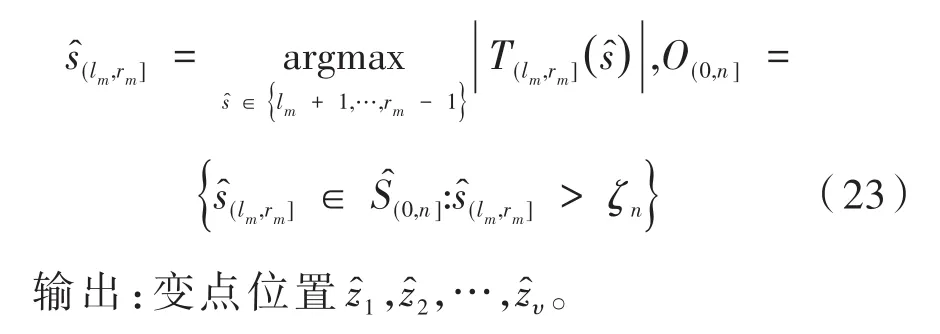
2 数值模拟
构造由模型1生成的具有均值变点的高维数据时,设置参数σ2=1,数据量n分别取200,500,1 000,2 000,维数p分别为200,500,1 200,将高维数据噪声表示为ε,分别取0.1,0.5,0.7,1,变点位置满足z/n={0 .25,0.5,0.75},定义ϑ(i)为第i个变点的均值跳跃大小,=(ϑ(1),ϑ(2),ϑ(3))=(0.4,0.8,1.2),ϑ(0)=0,,其中k控制着发生变化维度数量的稀疏程度,取值分别为10,40。根据文献[10]的建议,。根据文献[12]的建议,设置衰减参数a= 2。另外,下面三种情形分别考虑了均值结构中发生变化的维数坐标(p)上的重叠问题,高维数据中均值结构发生变化的三种不同重叠情形说明如下:
情形1(S1):在没有重叠的情况下,对于相应的变点,发生变化的k个维数坐标是来自完全不相交的坐标集;
情形3(S3):在完全重叠的情况下,则对于相应的变点,变化的维数发生在相同的k个坐标上。
本文先给出了SOP-SeedBS方法在情形3下,参数设置为σ2=1,n=2 000,p=200,k=40,ϑ̂=(ϑ(1),ϑ(2),ϑ(3))=(0.4,0.8,1.2),变点位置z/n={0.25,0.5,0.75}时,不同噪声下的变点估计结果可视化,用ε表示高维数据的噪声,不同ε取值对于投影后一维数据的变点检验结果如图2所示,图2的结果显示了当ε的取值越小时,噪声越小,分段特征越明显。另外,当均值跳跃越大,分段特征也越明显。后续的仿真实验中,噪声ε皆设置为1。

图2 不同 ε下的投影后一维数据的变点检验结果
表1给出了σ2=1时,SOP-SeedBS方法和Inspect方法的比较结果,两种方法在四组不同的参数设置M1、M2、M3、M4下,且每组参数设置都具有三种不同的情形,通过100次运行算法(两种方法通过相同参数设置下生成的高维数据进行比较)检测到的变点数量的频数和平均Hausdorff距离dH分别来度量估计变点的数量和估计变点位置的准确度。M1的参数设置为n=2 000,p=200,k=10,=(0.8,1.6,2.4);M2的参数设置为n=2 000,p=200,k=40,=(0.4,0.8,1.2);M3的参数设置为n=500,p=500,k=40,=(0.4,0.8,1.2);M4的参数设置为n=200,p=500,k=40,=(0.4,0.8,1.2)。表中Z1,Z2,Z3,Z4,Z5表示估计到的变点个数,取值分别为1,2,3,4,5。
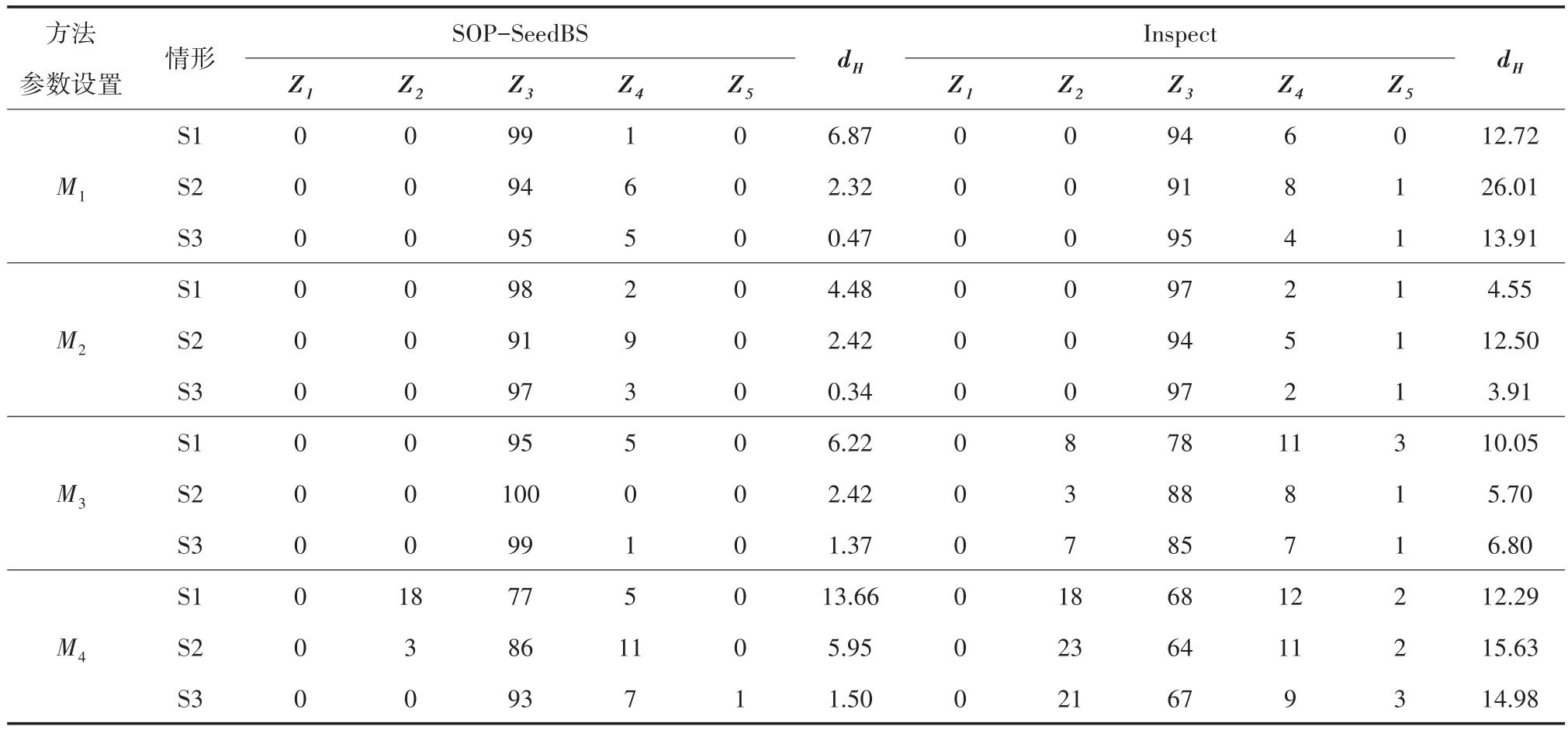
表1 两种方法在不同参数设置下进行100次模拟的估计变点频数和平均Hausdorff距离的比较
从表1可以看出,在σ2=1,n=2 000,p=200,k=10的参数设置下,SOP-SeedBS方法在三种不同均值变化重叠情况下的结果都优于Inspect方法,进行100次模拟的平均Hausdorff距离分别为 6.87,2.32,0.47,而 Inspect方法分别为12.72,26.01,13.91;第二组实验将第一组实验中的发生变化的维数k=10替换为k=40,第一个变点的均值跳跃大小由0.8变为0.4,SOPSeedBS方法在三种情形下进行100次模拟得到的平均Hausdorff距离分别为4.48,2.42,0.34。虽然两组实验在变点频数上同样具有良好的检验结果,但第二组结果与第一组相比,在均值跳跃变小的情况下,第二组结果中情形1和情形3的平均Hausdorff距离要比第一组更小,说明k的大小也会对实验结果产生影响。
从SOP-SeedBS方法的第三组和第四组实验结果可以看出,在其他参数固定的情况下,n越大,对比实验结果显示n较大时检验结果较好,说明由于样本量的增加,适当增加种子区间的个数有利于进行变点检验。本文还通过模拟实验发现,当其他参数固定时,维度p变大,对比实验的结果表现出检验效果相近,因此维度的增加对于变点检验效果影响不大。
图3给出了SOP-SeedBS方法与Inspect方法在其他参数不变的情况下,不同的n和p设置下算法平均运算时间的比较,可以看出SOP-SeedBS方法在算法运算速度上具有较大的优势。图3(a)给出了当p=200,n分别为 500、1 000、2 000时,两种方法100次模拟的平均运算时间;图3(b)给出了当p=500,n分别为 200、500、1 000时,两种方法进行100次模拟的平均运算时间。
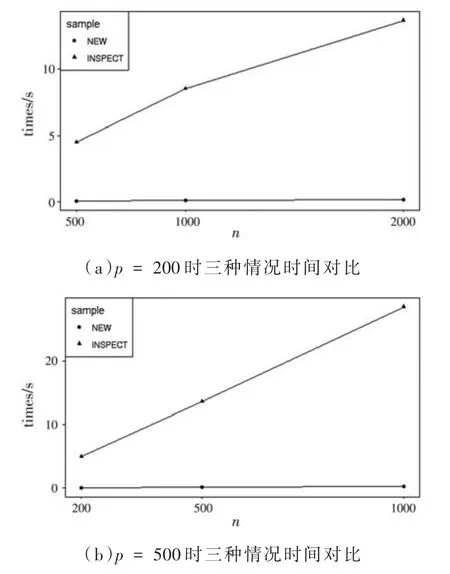
图3 SOP-SeedBS方法与Inspect方法计算时间比较
图3中的结果显示,当p=200,n=2 000时,Inspect方法进行100次模拟的平均运算时间达到了13.7 s,而SOP-SeedBS方法的平均运算时间仅为0.14 s,约是Inspect方法运算时间的1%。当p=500,n=500,Inspect方法进行 100次模拟的平均运算时间是13.6 s,而SOP-SeedBS方法的平均运算时间仅为0.15 s,约是Inspect方法运算时间的1%,由此能体现SOP-SeedBS方法在运算时间上优于Inspect方法。
为了研究变点间隔对实验结果准确性的影响,从前面的对比实验表1中发现,当均值变化为情形1时,SOP-SeedBS方法的效果不如情形2和情形3的情况,这也符合不同变点在不同稀疏维数坐标中发生变化时,信号强度会减弱的预期效果。因此,表2显示的是在情形1下的模拟结果,即发生变化的k个维数坐标是来自完全不相交的坐标集。表中Z1、Z2、Z3、Z4表示估计到的变点个数,取值分别为1,2,3,4。

表2 不同变点间隔在p=200,σ2=1时四组不同参数设置下100次模拟的结果
表2中有四组不同的参数设置B1,B2,B3,B4,其中B1的参数设置为zi+1-zi=20,表示相邻变点之间间隔20个数据,信号的均值跳跃大小为=(0.8,1.6,2.4);B2的参数设置为zi+1-zi=30,=(0.8,1.6,2.4);B3参数设置为zi+1-zi=40,=(0.8,1.6,2.4);B4的参数设置为zi+1-zi=50,=(0.8,1.6,2.4)。从表2的结果可以看出,通过模型1生成的四组不同参数设置下的变点数据,在σ2=1,p=200,n=2 000,k=40,变点间隔为20时,真实变点个数为3,三个变点的均值跳跃大小分别为 0.6、1.2、1.8,SOP-SeedBS方法在100次模拟中估计正确变点个数次数仅为 31 次,而在σ2=1、p=200、n=2 000、k=60时,100次模拟中估计正确变点个数次数仅有61次。由最后一组实验可以看出当变点之间的间隔达到50个数据点及以上时,SOP-SeedBS方法不仅能稳定地检测到正确的变点个数,在准确性上也能达到很好的效果。
3 实证分析
本节研究了R中ecp包的膀胱肿瘤微阵列数据集(Bladder Tumor Micro-Array Data),目的是检验样本目标区域染色体拷贝数的变化,常常用于医学中检验癌症的研究,染色体拷贝数变化反映了DNA的扩增和骤减。从医学的角度来说,扩增的片段可能存在致癌基因,骤减的片段可能存在抑癌基因。本文对数据集中43个个体(p)的基因组上的2 215个不同基因位点(n)的对数强度比测量值进行检验,图4绘制了前10个个体在前200个基因位点上的对数强度比散点图,并采用SOP-SeedBS方法估计变点位置(其中虚线表示检测到的变点位置),同时给出了文献[10]和文献[14]中Inspect方法和 Adapt-WBS方法的检验结果,来验证SOP-SeedBS方法的有效性。

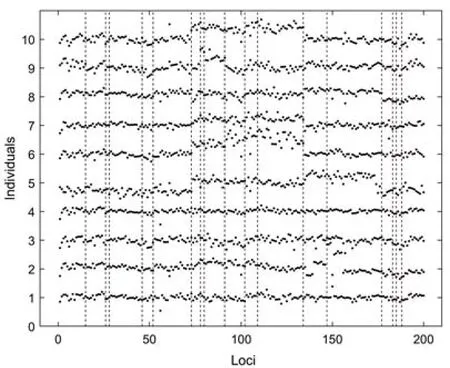
图4 前10个个体在前200个位点上的ACGH数据散点图
从图4中可以看出,SOP-SeedBS方法检测到的变点结果为:15,26,28,52(56),73,91,102,134,147(146),177(174),183(180),185(186),188(191),与文献[10]和文献[14]中检验到的变点相近,其他无法检测到的变点,例如位点30到40之间的数据出现的分段特征不明显,许多个体在位点110~130之间测量值分布较为分散,没有呈现出明显的分段特征,位点155附近的测量值分布非常分散。SOP-SeedBS算法的结果与Inspect的结果的相似度约为80%。
4 结论与展望
本文提出SOP-SeedBS方法结合了奇异值分解和投影的思想,通过分析高维稀疏变点数据的特点,对数据矩阵进行奇异值分解找到一个最优的投影方向,将存在稀疏变点的高维数据沿着最优的投影方向投影成一维数据,再利用SeedBS方法对一维数据进行多变点检验。通过仿真实验,分别用变点检验频数和平均Hausdorff距离评估了变点检验的准确度。本文提出的SOP-SeedBS方法在运算时间、算法准确度上都优于Inspect方法,特别是在时间上具有较大的优势。最后将SOP-SeedBS方法应用于ecp包中的膀胱肿瘤微阵列数据集中,检验结果与文献[14]中给出的Inspect方法的检验结果有约80%的相似度。
本文是先将高维数据投影到一维,再进行变点检验。进一步还可以研究能否在保持数据维度不变的情况下,通过某种方式,例如引入一种针对高维数据的检验统计量,将SeedBS方法直接用于高维数据的变点检验问题中。

