液氮冷刀共轭传热模型消融肿瘤的研究
公维芳,曹秒,王彬
(长春理工大学 生命科学技术学院,长春 130022)
恶性肿瘤是全球第二大死因,在未来的二十年中全世界癌症病例数可能会增加60%[1]。尽管外科手术是肿瘤治疗的首选方法,但是大部分病人在明确诊断时肿瘤进展已处于中晚期,能获得手术机会的病人约为20%~30%。近年来,临床上逐渐开始应用新兴的肿瘤疗法[2],低温冷冻手术作为一种微创物理疗法,具有创伤小、恢复快等优点[3],使得一些不耐受手术的多发性肿瘤转移的患者获得延长生存期甚至获得根治肿瘤的机会。
冷冻消融手术兼顾创伤小和治疗效果是非常困难的,因为监测冻结过程这一技术难题限制了冷冻消融手术在临床应用上的推广,因此模拟研究就显得格外重要。Kumar等人[4]通过双曲线和抛物线型两种模型模拟了肺癌手术数值仿真过程中的相变传热过程。舒春等人[5]采用浸入边界法来研究冷冻过程中血管的热效应,并将仿真结果与已发表的结果对比验证,结果吻合。CHAPAL S M等人[6]提出了瞬态三维两相制冷模型来评估前列腺手术最佳冷冻效果,通过数值计算研究了组织内特定点的温度分布。GOLKAR E[7]提出基于GPU的三维冰球快速建模方法预测冰球直径,仿真实验验证结果是误差仅在冰球直径的5.8。SHARMA等人[8]仿真过程中加入导热系数低的全氟乙烷以达到快速冻结的目的。本文采用液氮为一相,液氮蒸发气化为二相的双相流共轭传热模型对冷刀的物理行为进行建模,并在气泡填充法基础上进行了计算优化,此模型可用于分析冷刀插入深度、结构参数及放置位置对消融结果的影响。
1 求解生物传热方程
冷刀共轭传热模型为应用于微小圆管通道的流体模型,即流体流经一个空间位置固定的微团,因此其连续性方程可以写为如下形式:
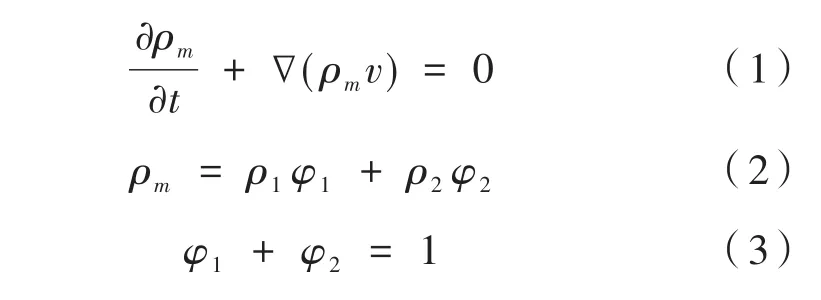
其中,ρm为液氮混合相密度;v为液氮平均流速;ρ1为液氮一相密度;φ1为一相体积分数;ρ2为二相密度;φ2为二相体积分数。
生物组织间的耦合传热可由Pennes生物传热方程描述[9]:
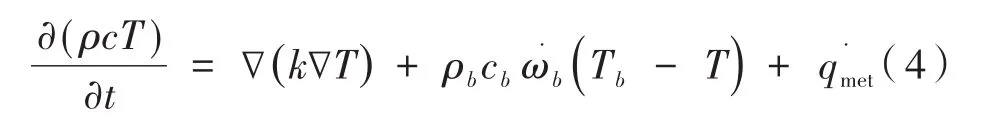
其中,T为组织温度;ρ为密度;cb为血液的比热;为血液灌注率;体积代谢热(肿瘤:,正常组织:);下标b表示血液。
在组织冻结过程中,相变往往发生在很小的时间范围(Tl,Ts)内,其中上转变温度Tl=1 ℃,下转变温度Ts=-8℃,引入比热和导热系数方程,作为肿瘤内部热源:
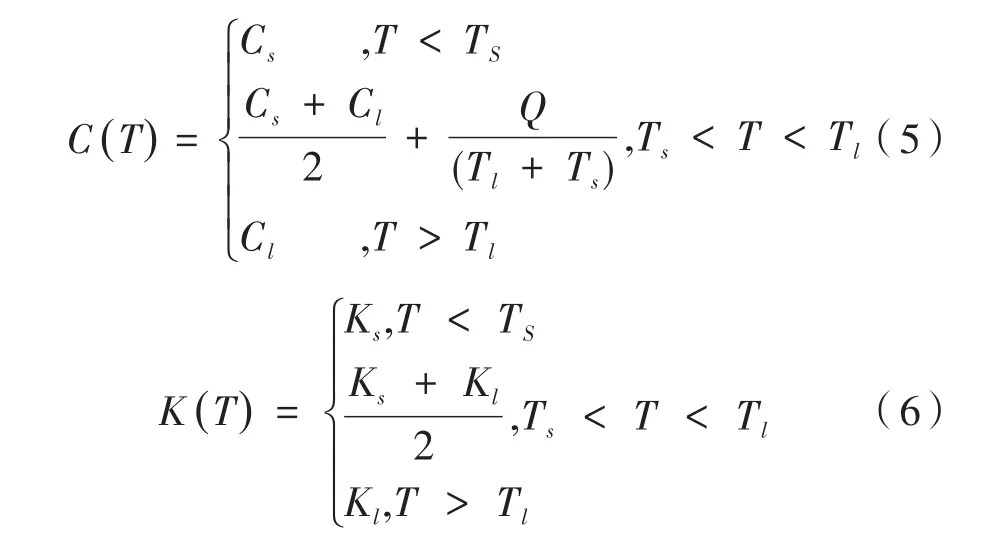
其中,Cs=1977J/(kg·℃)是冻结组织的比热;Cl=3688J/(kg·℃)是未冻结组织的比热;Ks=1W/(m·℃)是冻结组织的导热系数;Kl=0.42 W/(m·℃)是未冻结组织的导热系数,Q=250 MJ/Kg是组织潜热。
2 共轭传热模型建立及数值计算过程
液氮冷冻刀内部的流体流动和传热是不稳定的瞬态相变现象,从而使冷冻过程无法控制,无法实时精确监测冷冻效果,而数值计算和仿真研究可以在计算机上通过设定条件来模拟实验所需环境和实验过程,精确的物理模型可以帮助研究者通过冷刀和生物组织的相互作用来分析和监测冷冻消融手术过程中的温度分布和消融体积变化情况。
单个冷冻刀仅可完全摧毁径向长度小于2 cm的肿瘤,当肿瘤大于等于3 cm时就需要多个冷刀相互协助消融[10]。而三个直径为3 mm的冷刀可在相对较短的冷冻时间内杀死肿瘤细胞,并尽可能减少对健康细胞的损伤[11]。建立的模型如图1所示,包括圆柱形健康组织,球形肿瘤组织,以及由内外同心管组成的冷刀,冷刀采用不锈钢材质内外管底端距离5 mm,内管直径为可调节的,外管直径为3 mm,绝热段42 mm传热段8 mm,其中组织顶部暴露在空气中进行对流换热,模型周围设定为恒定体温37℃。为了研究温度随时间变化的趋势,取P2、P3、P4点分别距离冷刀5 mm、15 mm、10 mm,在仿真过程中记录测温点的温度变化,用来评估冷刀的制冷效果。
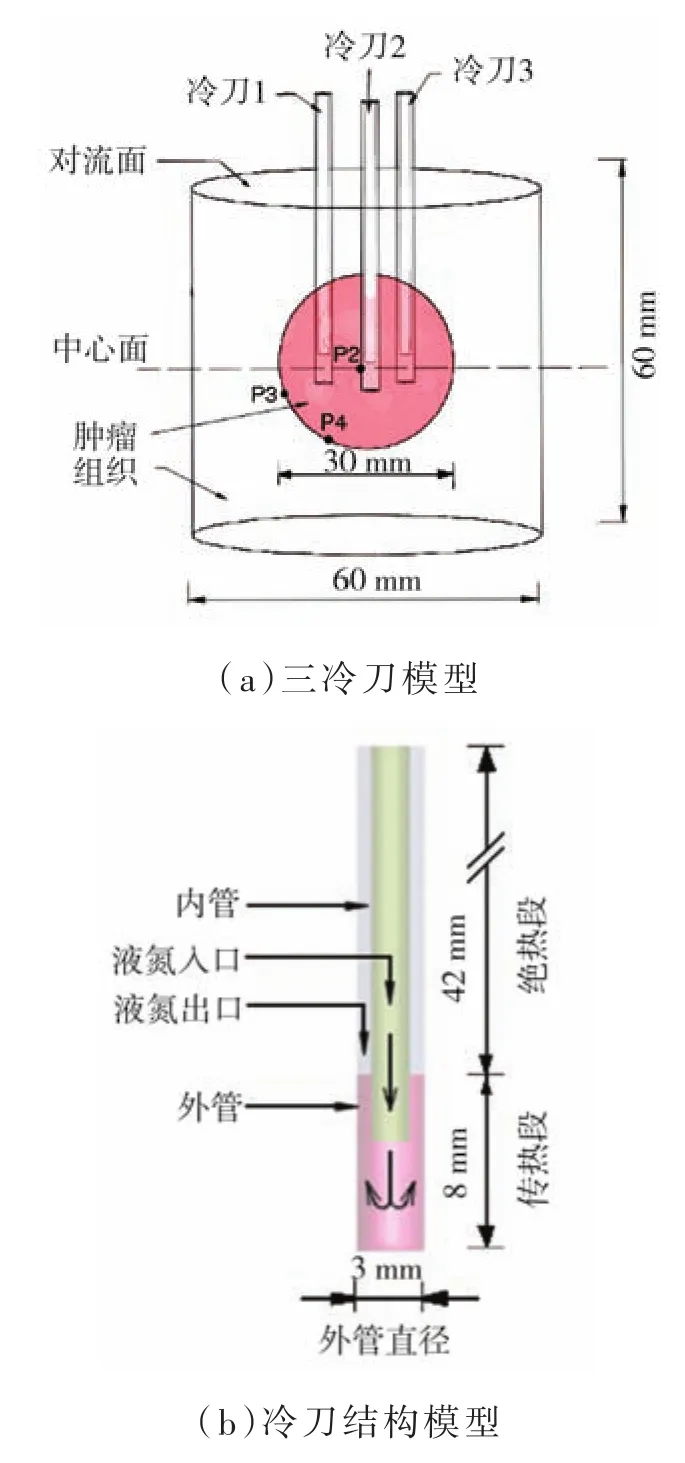
图1 肿瘤消融三维模型和冷刀结构模型
采用有限元离散软件Fluent对液氮冷刀模型进行数值仿真计算,采用GAMBIT对肿瘤冷刀模型网格划分[12],由于网格疏密对数值计算结果有一定的影响,计算结果的精确度随网格数量的增加而提高,与此同时会造成计算量增大、计算周期增长的问题。因此做以下两点处理:首先进行网格无关性验证,所谓网格无关性即在计算精度和计算开销间寻求合适的点,这个点所处的位置就达到了网格无关性的阈值;其次在需要着重研究的冷刀传热段采用较密的划分,肿瘤区域次之,健康组织采用较稀的网格数量。如表1所示,网格数量60 W和80 W消融体积差小于1%,结合计算效率,选取60 W网格对应数值来进行仿真计算。

表1 网格无关性验证
求解过程选择基于压力的瞬态求解模式,并应用Eulerian模型来计算双相流问题,选择能量方程作为控制方程,冷刀入口处雷诺数为20 000,K-epsilon Realizable黏度模型实现对液氮冷刀的数值求解。该模型的湍动能及耗散率运输方程为:
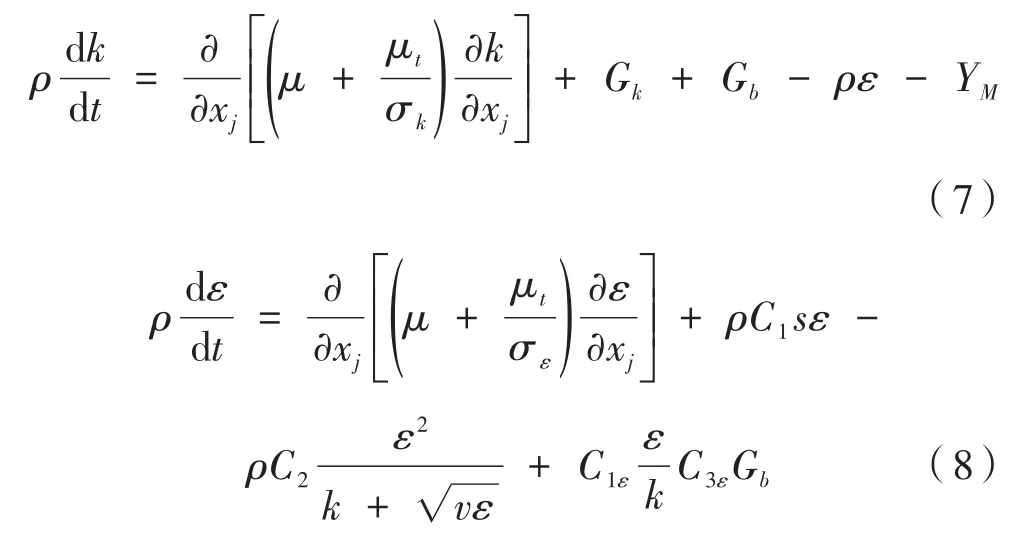
其中,Gk表示由于平均速度梯度引起的湍动能产生;Gb是浮力引起的湍动能产生;YM是可压缩湍流脉动膨胀对总的耗散率的影响;C2和C1ε是常数,分别为1.9和1.44;σk和σε分别是湍动能及其耗散率的湍流普朗特数,作为默认值常数分别为1.0和1.2。
通过将数值计算的预测结果与张鑫等人[13]公布的实验结果进行比较,验证了两相流共轭传热冷刀模型预测生物组织内部温度分布的有效性。
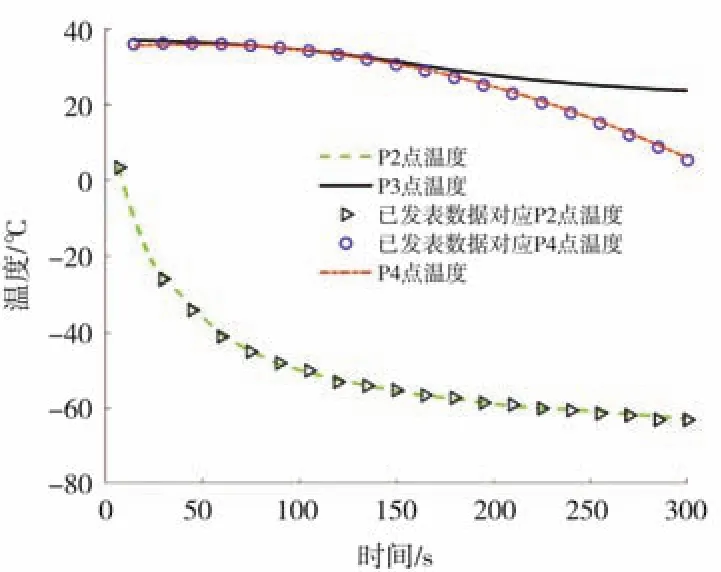
图2 测温点温度对比图
3 气泡填充法的优化
气泡填充法是一种基于计算机的规划方法,用于在指定区域内使一定数量的气泡受力不断运动直至均匀分布的物理方法[14]。该方法首先在给定区域内形成球形气泡,假设气泡间受到类似范德华力的作用,通过施加物理意义上的张弛找到紧密的力平衡的气泡排列。此外沿着目标区域的轮廓还放置了一组静止的气泡作为边界气泡。根据文献[15],简化的范德华力模型如下:
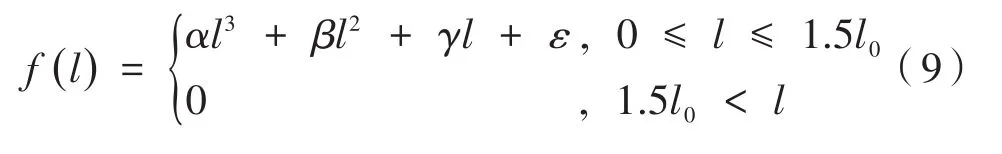
边界条件如下:
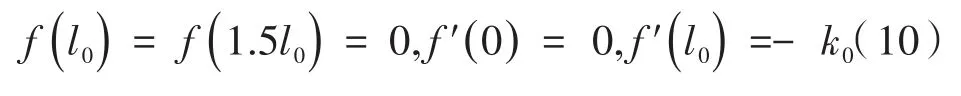
其中,l是两个相互作用的气泡间的实际距离;l0是相互作用的气泡间的稳定距离;k0是距离为l0时的线性常数;α、β、γ、ε是简化范德华力模型的系数。
在目前研究中,所有气泡的大小和形状在趋于平衡的过程中是保持不变的[16],气泡的尺寸是根据目标区域的大小、正在使用的低温探针数量来选择的。因此,气泡体积如下:
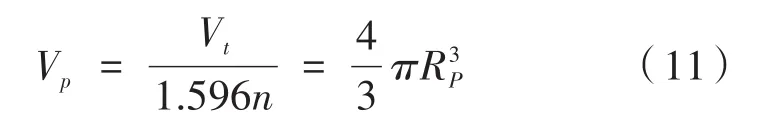
其中,Vp是气泡的体积大小;Vt是目标区域的体积大小;n为此次消融的气泡数量,即对应的冷刀数量;RP是气泡轴向半径;1.596为此模型通过反复实验得出,可用于所提出的肝部肿瘤模型。由于肝部肿瘤模型内无特殊热源,所以冷刀横向布局应为均匀分布,即θ=60°。若想达到最佳消融效果,既要得到最大的冰球覆盖面积又要保全健康组织,即令冷冻治疗范围超过肿瘤2 mm左右。已知肿瘤半径Rt,所以根据三角函数公式计算得到冷刀间距d:
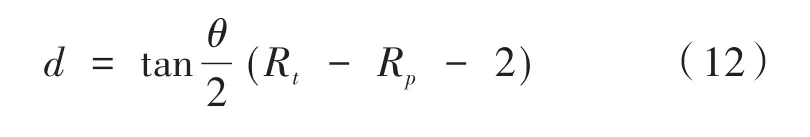
4 实验结果与分析
4.1 冷刀插入深度及长径比影响分析
冷冻手术的第一步就是要确定冷刀插入深度,由实验可得冷刀在冷冻过程中形成的消融体积是椭球形,其中单个冷刀消融的轴向和径向直径可达到9 mm和11.6 mm。随着消融时间的增加,冷冻范围逐渐逼近健康组织,所以确定插入深度可以有效减少健康组织的损伤。由图2可以直观看出,传热段8 mm的冷刀插入肿瘤10 mm在消融至300 s时,冷冻范围距健康组织过近会导致组织不可逆的损伤,与插入肿瘤12 mm和14 mm模型对比可知插入深度14 mm冷冻范围居肿瘤中心,为适宜的插入深度。
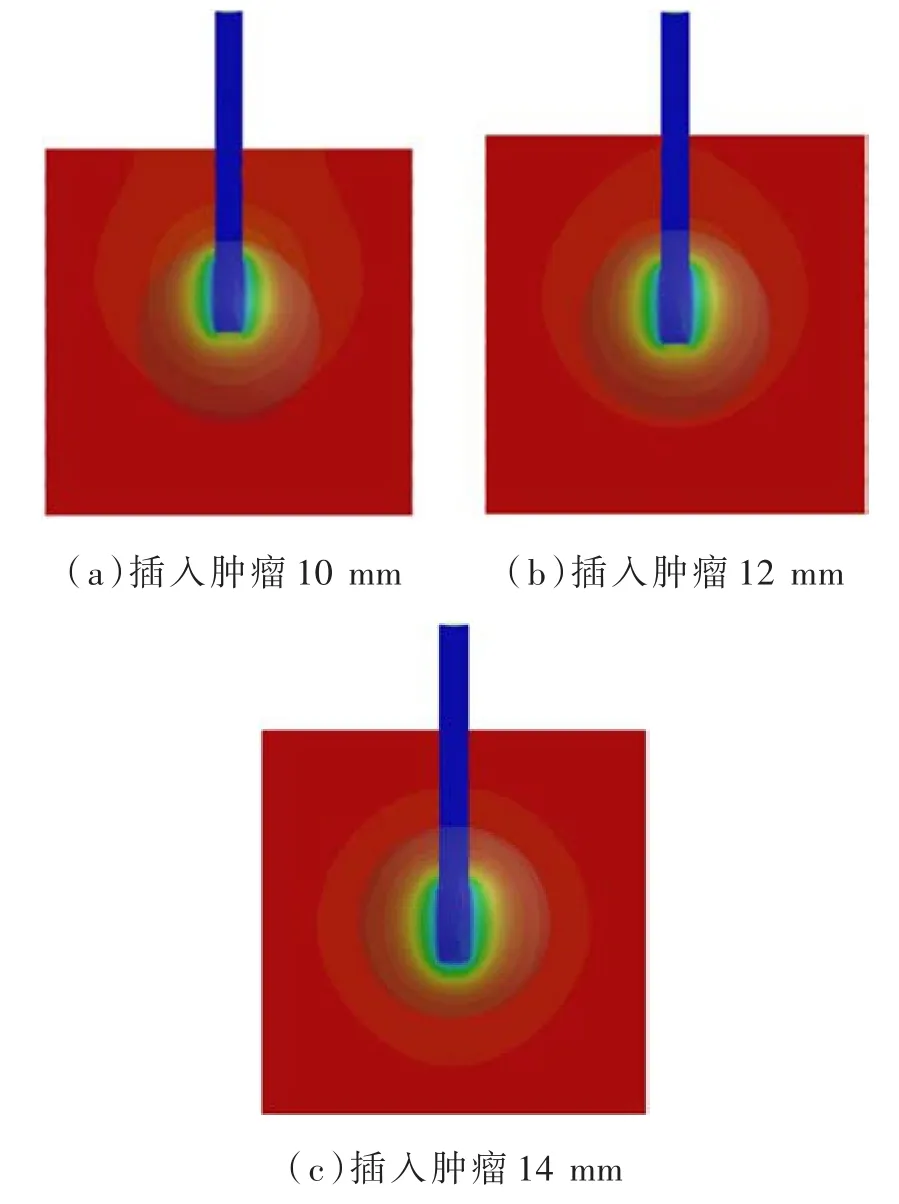
图3 冷刀插入深度温度分布图
冷刀内管是液氮流入的通道,管径的大小影响冷刀头处的液氮流速,而液氮流速的改变进一步影响组织间的换热过程和组织中产生的温度分布,因此做了以下三组模型进行对比分析。图3为直径不同的三组冷刀模型流速矢量图,由图可以看出内管直径越小形成的湍流窝越小,液氮流下撞击管壁造成冷刀震荡越强烈,比较后得出内管直径1.8 mm的冷刀模型速度矢量图形成的湍流较为规则。消融情况由图4验证可得,内管直径1.8 mm的冷刀模型消融体积最大,300 s时单冷刀消融体积达到0.681 5 cm3,而内管直径继续增加会对回流产生巨大阻碍,因此选用1.8 mm的内管直径做进一步的研究。

图4 不同内管直径的冷刀头液氮流速矢量图
4.2 冷刀布局对肝肿瘤的消融结果
由式(10)计算得出最佳冷刀间距为14 mm,图5是其在-22℃下消融体积随时间变化图。由图5知150 s时模型热耦合区域(中心区域)未见明显空隙,这是冷量叠加的效果,即在一定距离范围内,冷刀间存在协同作用。对间距为13 mm和15 mm的冷刀布局模型仿真计算做进一步验证,其消融体积及各测温点温度如图6所示,间距为14 mm的冷刀模型消融效果最佳。冷刀间距越小,中心热耦合区域温度越低,随冷刀间距增大,近冷刀端p3温度越低,而远冷刀端p4温度差异不大。实验表明随着治疗时间的增加,冷刀间距增大会加重对健康组织的损伤,而冷刀间距为14 mm模型的远冷刀端温度最低,在得到最大消融体积的同时满足对健康组织损伤较小的要求。
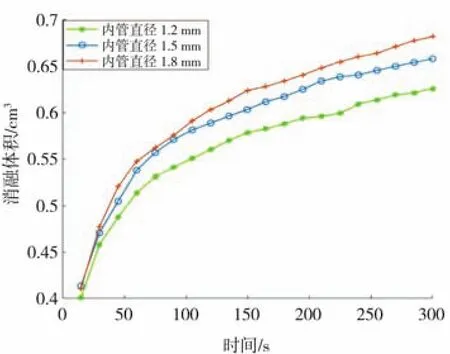
图5 不同内管直径模型300 s消融体积图
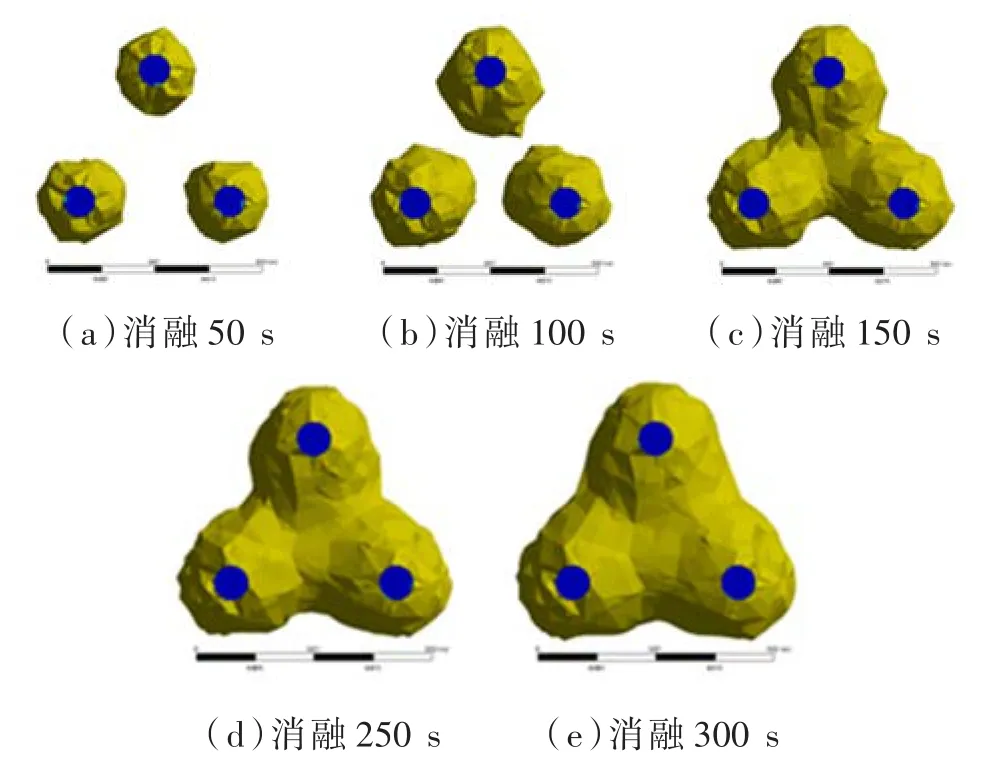
图6 冷刀间距为14 mm的模型-22℃等温线体积图

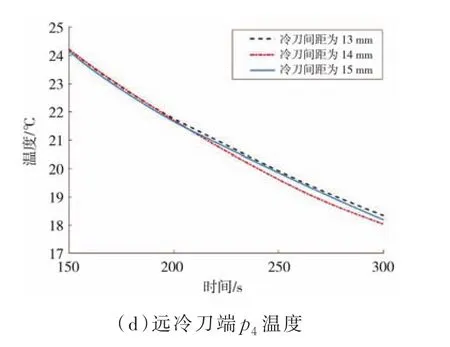
图7 二维模型消融体积及温度变化曲线
5 结论
基于有限元数值仿真方法建立了双相流共轭传热模型,并应用了改进的气泡填充法,分析了三个液氮冷刀应用于肝脏肿瘤的三组模型的消融结果并对其进行比较。随着消融时间的增加,可形成椭球形消融区域,为减少健康组织损伤并保证消融效果,计算并比较了不同的冷刀插入深度、内管直径和冷刀间距在目标区域及健康组织的温度分布情况。最终得出插入深度为14 mm,冷刀内管直径为1.8 mm,间距为14 mm时的多冷刀布局具有很好的消融效果。

