基于彗差和像点偏移的大口径望远镜次镜姿态校正

朱 熠，王建立，陈 涛，吴小霞，李宏壮

（中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033）

1 引 言

为了克服重力、环境温度和镜体加速度等因素对大口径主镜面形精度的影响，在望远镜系统运行中校正和维持主镜镜面的面形精度，保证后端成像系统的成像质量，3 m 级以上的大口径望远镜均基本采用主动光学技术［1-3］。主动光学由R.N. Wilson，F. Franza 和L. Noethe 于1987 年 提出，并应用于ESO New Technology Telescope（NTT）3.58 m 大口径望远镜的主镜支撑［4］。主动光学系统不仅要协同波前检测系统和力促动器，主动检测和校正主镜镜面面形，实现主镜主动支撑；还需要维持主镜和次镜的相对位置，保证后端成像质量。

针对同轴双反射镜系统，可通过焦点偏心、轴上彗差、轴外三叶像差等参数获得主次镜之间的光轴偏离量，进行光路装调修正［5-9］。该方法同样适用于主动光学系统的次镜姿态控制。当主镜位置闭环稳定控制后，通过上述参数的测量和解算，能够得到次镜当前的姿态误差量，从而进行反馈修正。本文针对大口径望远镜主动光学系统次镜的姿态控制需求，结合前述的同轴双镜系统光轴对准方法，建立了一种基于波前检测和像点偏移的次镜姿态校正方法，通过大口径望远镜主动光学系统的夏克-哈特曼波前传感器和用于对准的成像相机的采集数据，解算次镜姿态误差，并通过次镜六自由度平台进行补偿校正。

2 次镜姿态校正方法

图1 为大型望远镜典型主动光学系统原理图。本文提出了基于次镜的近轴曲率中心点和近轴无彗差点的次镜姿态校正方法。曲率中心点为次镜顶点处曲率半径对应的球心，当次镜以曲率中心点为球心，沿球面小幅值旋转时，不会改变焦平面焦点位置，即像点偏移量不变。次镜以无彗差点为球心，沿球面小幅值旋转时，不会改变轴上波前像差中的彗差分量。

图1 主动光学系统原理图Fig.1 Schematic diagram of active optics system

无彗差点的位置受次镜镜面种类的影响。卡塞格林式望远镜的无彗差点坐标计算公式为［10］：

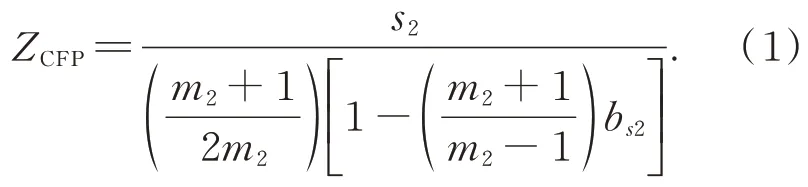
式中：s2为次镜与主镜主焦点之间的距离；m2为次镜的几何角放大率，m2=μ1/μ2；bs2为次镜非球面度，如图2 所示。

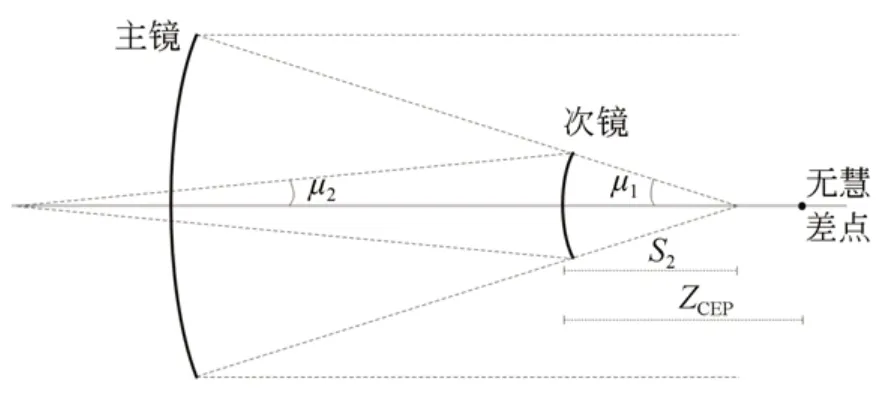
图2 主次镜系统无彗差点相关参数Fig.2 Parameters of coma free point of primary and secondary mirrors

当次镜镜面为非球面时，bs2≠0 时，次镜无彗差点与次镜曲率中心点不重合，可以通过无彗差点和曲率中心点实现次镜姿态校正。其基本流程为：首先检测次镜后端焦平面上像点的偏移量，并基于次镜无彗差点校正焦平面的像点位置，使像点位于视场中心；然后，采集次镜后端轴上的波前像差，提取其中的彗差分量，并基于次镜曲率中心点校正彗差，修正光路对准。

次镜姿态具有6 个自由度，按次镜光轴定义直角坐标系z轴，则6 自由度分别为x，y，z方向的平移和旋转。由于同轴系统次镜为旋转对称镜面，z轴旋转无影响，次镜姿态调整需求为次镜的x，y，z方向平移和x，y轴旋转的调整，如图3 所示。其中，z方向平移对应离焦，用于系统调焦；x，y方向平移和x，y轴旋转耦合为焦平面像点的偏移和轴上彗差，以曲率中心点和无彗差点为基准旋转次镜进行补偿校正。为此，针对次镜可能产生的姿态误差，除了系统离焦量，还需要提供4个自由度的姿态误差检测。次镜以一点为球心沿球面旋转，可分解为次镜以该点为圆心在两个垂直方向旋转，即等效为耦合x，y方向平移和x，y轴旋转的2 个自由度的姿态调整。因此，当次镜曲率中心点和无彗差点不重合时，曲率中心点与无彗差点分别提供2 个自由度的次镜姿态调整，能够校正次镜x，y方向的平移和x，y轴的旋转。

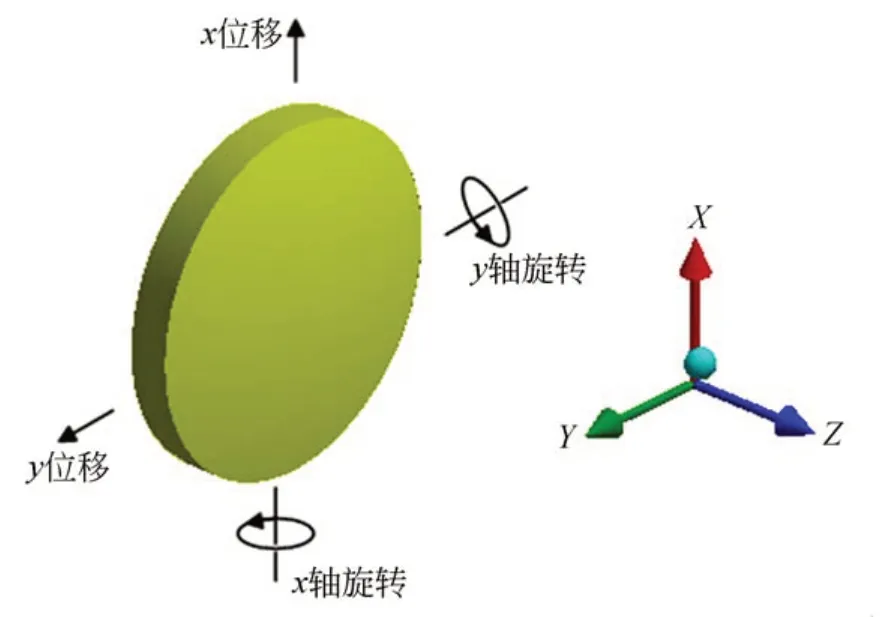
图3 次镜姿态的4 个自由度Fig.3 Four DOF of secondary mirror’s attitude

3 仿 真

本文通过Zemax 进行光学建模，并通过matlab 进行望远镜主次镜系统，以及基于设计参数的望远镜次镜等效无彗差点的仿真计算，以验证本文提出的次镜姿态校正方法的有效性。

在Zemax 仿真环境下建立望远镜的主次镜光路及后端成像焦面光路，并将焦平面定义为像面。正入射的平行光经过主次三镜反射后进入波前检测光路，并汇聚在焦平面。次镜姿态正确时，焦点位于光轴上，即像点位于像面中心，同时无彗差。当次镜处于错误姿态时，则会出现像点偏离像面中心，或者像点出现彗差。图4 为Zemax 仿真光路模型。

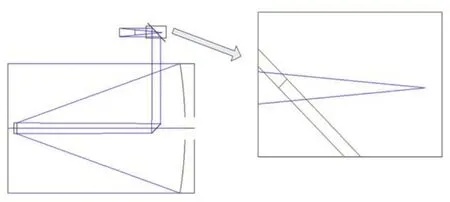
图4 Zemax 光路模型2D 图Fig.4 Two-dimensional diagram of Zemax optical model

通过4 m 望远镜主次镜仿真模型的仿真计算，验证采用曲率中心点校正彗差的能力。然后，在仿真模型上以标定拟合法计算次镜无彗差点的位置，确定无彗差点的有效性；同时，确认曲率中心点和无彗差点位置具有足够大的差异，能够实现有效的次镜姿态校正。

3.1 曲率中心点仿真

通过在仿真模型上对次镜进行平移和自转，实现次镜沿曲率中心点的近轴旋转，并由此仿真计算次镜沿曲率中心点引入的彗差变化。次镜沿某个圆心在x方向旋转α，在近轴等效于次镜在x方向的位移d及绕y轴的自转β，且：

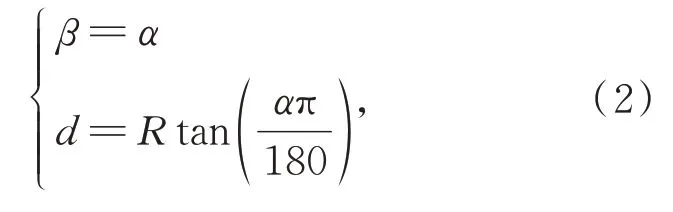
其中R为旋转半径，当R设置为曲率半径时即为沿曲率中心点旋转。由于次镜镜面旋转对称，因此单个方向的旋转仿真足够验证各个方向的特性。本文采用x方向旋转，即次镜x方向平移和y轴自转。

图5 为次镜以曲率中心点为圆心，x方向正向旋转的旋转角度与由此引入的轴上彗差（x向彗差）及拟合曲线，图6 为不同旋转角度对应的像点形状。在近轴范围内（＜0.4°），次镜绕曲率中心旋转角度与彗差量呈良好的线性关系，因此通过波前检测得到的轴上彗差，快速精确地计算出彗差校正对应的次镜姿态调整量。当旋转角度在0.1°时，引入的彗差量约为4.4 μm。主动光学系统进行次镜姿态校正时，待校正的彗差量级一般在±1λ（λ=0.633 μm），对应的次镜调整量为：平移14.6 mm，旋转0.014°。次镜调整机构的位移精度应在0.1 mm 以上，旋转精度在0.001°以上。

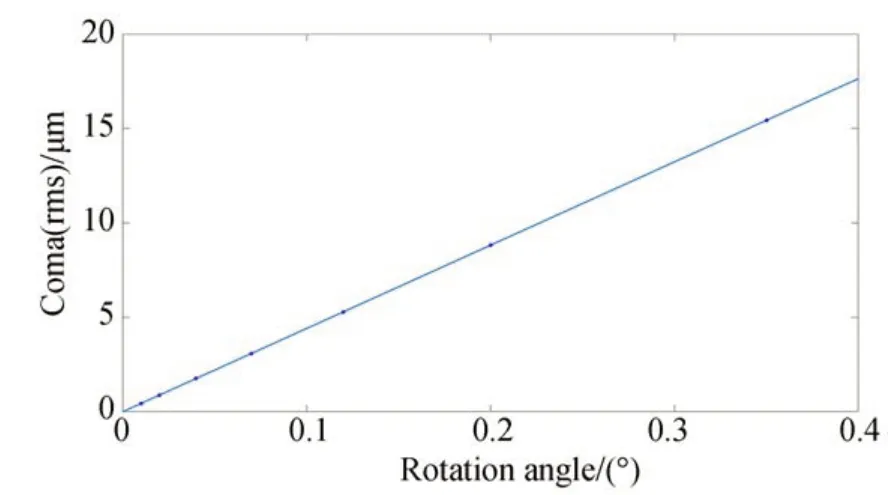
图5 次镜基于曲率中心旋转指定角度与彗差的关系Fig.5 Relationship between angle of rotation by center of curvature and coma

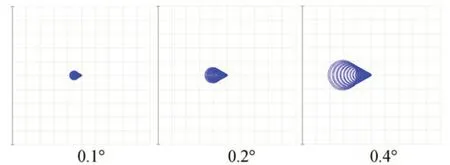
图6 次镜基于曲率中心旋转指定角度后的像点弥散Fig.6 Simulation of image points after rotation by center of curvature

3.2 无彗差点仿真

通过在仿真模型的次镜上施加平移和自转，进行无彗差点的仿真计算。式（1）的主次镜系统无彗差点计算为次镜旋转对应彗差和次镜平移对应彗差在近轴小幅值条件下为线性映射，由此得到一个等效无彗差点，沿该点做圆面运动不引入彗差。将次镜沿一个方向自转一个角度，由此产生轴上彗差；然后，通过对应方向的平移，补偿自转产生的彗差，并记录自转角度和平移距离，作为一组仿真标定数据。每组近轴标定数据能计算出一个无彗差点位置。不同幅值的多组近轴数据计算结果基本一致，说明存在稳定的无彗差点，可以通过无彗差点进行针对像点偏移的次镜姿态修正。

表1 为旋转0.01°～1.0°产生彗差后再通过平移抵消彗差的仿真结果。在近轴（0.5°以内），无彗差点位置基本稳定。对标定结果进行最小二乘线性拟合计算无彗差点半径，结果为-466.95 mm，即次镜无彗差点位于轴上次镜后端-466.95 mm。该点位置与曲率中心点位置（次镜后端-1 013.33 mm）具有明显差异，能有效地校正次镜姿态。

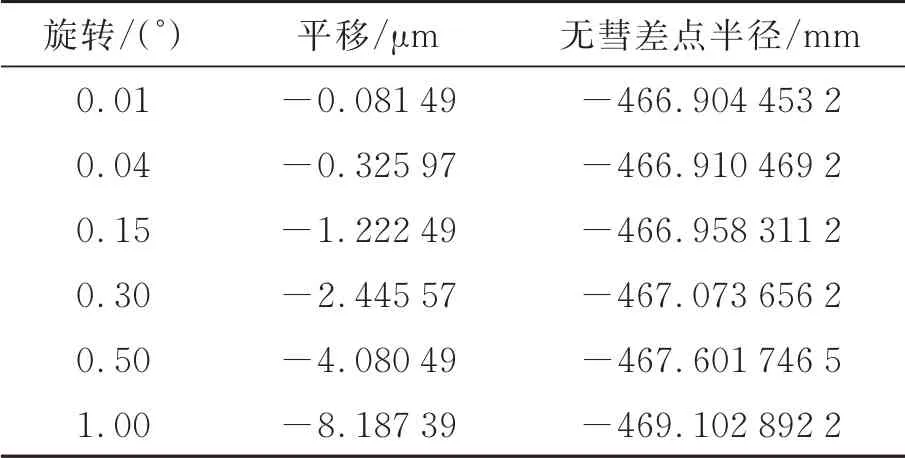
表1 无彗差点仿真标定结果Tab.1 Result of CFP calibration in Zemax

4 实 验

大口径光电成像望远镜全天区运行，且使用高分辨成像系统时，主要目标为低轨运动目标，观测过程中，可能存在大幅度的望远镜俯仰角变化。由于不同俯仰角的重力影响，由望远镜俯仰角变化引入的次镜姿态偏差较大，如果不进行补偿，会严重影响后端成像系统的工作性能。

4.1 次镜校正能力标定

采用天区位置稳定的北极星作为信标，并通过改变次镜六自由度平台位置调整次镜光路。首先，将像点调整至视场中心。望远镜继续指向北极星信标，将次镜沿无彗差点进行x轴旋转和y轴旋转，分别旋转0.031，0.063，0.113，0.188，0.281°，并记录对应的像点偏移量。图7 和图8为154″视 场 内 星 点 在x轴 旋 转0.031，0.113，0.281°和y轴旋转0.031，0.113，0.281°时的位置偏移，其偏移呈明显的线性比例，位移方向正交，且旋转后像点无彗尾形状特征，不引入额外的彗差。图9 为沿无彗差点旋转角度与产生的像点偏移量，以及曲线拟合。可以看出，检测标定数据呈明显的线性分布且两方向的变化速率一致，在近轴部分可以通过次镜无彗差点旋转实现快速精确的像点偏移校正。

图7 次镜基于无彗差点x 轴方向旋转指定角度后星点Fig.7 Star images with CFP x-axis rotation of secondary mirror

图8 次镜基于无彗差点y 轴方向旋转指定角度后星点Fig.8 Star images with CFP y-axis rotation of secondary mirror

图9 次镜x 轴方向旋转和y 轴方向旋转与像点偏移角度的拟合曲线Fig.9 Fitting lines of imaging point position and rotation of x-axis and y-axis

然后，沿曲率中心在x方向和y方向进行2°和4°的大幅值旋转，并引入1 mm 离焦，以观察波前变化影响。上述处理后的星点图如图10 所示，旋转后产生明显的彗差，且方向正交；尽管进行了大幅值旋转，引入了大幅值彗差，像点仍位于中心附近。因此，采用次镜曲率中心旋转，能有效校正次镜姿态误差引入的彗差。

图10 曲率中心旋转后的离焦星点图Fig.10 Unfocused star images with rotation of curvature center

4.2 次镜校正效果

图11 为次镜的校正效果。通过次镜校正，像点由偏移状态修正回视场中心；且像点由具有彗差特征的拖尾弥散斑，恢复为能量集中的圆形亮斑。在各个角度均进行次镜校正，保证像点处于视场中心，且像点无彗差特征，则可以保证望远镜在俯仰运动过程中次镜姿态保持正确。

图11 次镜校正前后的星点图及放大图Fig.11 Star images and scaled images with and without correction of secondary mirror

图12 为次镜无主动校正时的高分辨成像系统前端的精密跟踪对准系统在望远镜仰角变化时的像点图。在指向北极星（37°仰角）时，像点基本在十字靶标旁边，偏差为1.12″；指向11°低仰角时像点向左上偏移，偏差为7.12″；指向77°高仰角时，像点位于视场边界，偏差为12.85″。在高分辨成像系统工作时，需要精密跟踪系统控制快反镜调整光路，将像点维持在视场中心附近。当俯仰引入的像点偏移过大时，由快反镜修正引入的光轴指向偏差会影响高分辨成像系统的成像精度；更严重时，像点偏移量超出快反镜的动态范围，精密跟踪系统无法正常工作，导致高分辨成像系统无法成像。因此，需要采取次镜主动校正，以补偿仰角变化引入的像点偏移。

图12 无次镜校正时各角度精跟像点位置Fig.12 Imaging point positions at different elevations without correction of secondary mirror

图13 为加入次镜校正后，3 个俯仰角度下的精跟视场像点图。除了进行初始对准的指向北极星时的像点（37°）以外，在低俯仰角（24°）和高俯仰角（75°）时像点均在视场中心十字附近，最大偏差为1.80″。

图13 有次镜校正时各角度精跟像点位置Fig.13 Imaging point positions at different elevations with correction of secondary mirror

将上述有无次镜校正时的精跟像点偏移量进行整理，并绘制曲线，如图14 所示（彩图见期刊电子版）。其中，红色曲线为无次镜校正时不同仰角像点偏移采样数据以及拟合的曲线；蓝色曲线为有次镜校正时不同仰角像点偏移采样数据以及拟合的曲线。通过次镜校正，像点偏移幅度在2″以内，大幅减轻了精密跟踪系统闭环校正的负担，能够保证后端成像系统正常工作。

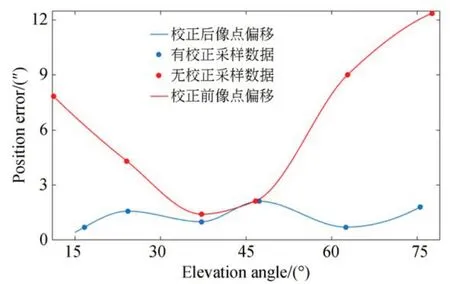
图14 有无次镜校正精跟视场像点偏心量Fig.14 Imaging point position error with and without correction of seconday mirror

5 结 论

本文基于大口径望远镜工作中俯仰角度变化下次镜姿态的调整需求，提出了一种基于次镜曲率中心和无彗差点的次镜姿态校正方法。通过Zemax 仿真验证了该方法的有效性，然后将该方法应用于大口径望远镜。实验结果表明：通过该方法校正次镜姿态，望远镜俯仰运动中次镜姿态引入的成像偏移由12.85″缩减至1.80″，有效降低了后端精密跟踪系统视场对准校正的负担，保证了高分辨成像系统的成像质量。

该方法将经典的无彗差点理论应用于大口径望远镜次镜姿态校正，简单易实现，效果显著，能够满足精密跟踪系统前端的光路粗对准需求，保证精密跟踪系统的正常运行。