大口径望远镜主次镜弯沉的精确测量

陈宝刚，王建立，张 岩

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009）

1 引 言

随着望远镜口径的不断增大，镜筒结构尺寸及质量越来越大，结构的有限刚度及重力场变化带来的主次镜空间位置变化也愈加明显，进而影响望远镜的成像质量及指向精度［1-4］。大口径自适应光学望远镜通常采用单独的粗跟踪望远镜进行图像闭环跟踪，跟踪过程中随着望远镜俯仰角不断变化，镜筒结构受重力影响而产生形变［5］，主次镜光轴与粗跟踪光轴之间不再保持装调时的平行状态。这种主次镜位置关系的变化不仅会影响主系统波像差，造成后面光学终端的成像质量下降；还会影响焦点的成像位置，引入指向误差，造成波前传感器的光瞳位置偏移，降低自适应光学系统的校正效果。所以，主次镜空间位置关系的高精度稳定是望远镜成像质量的重要保障。

传统方法是在望远镜前后镜筒设计不同刚度的桁架结构，匹配主镜室与次镜组件的重量，最终保证主次镜的相对位置尽量不变［6］。目前，通常是给次镜组件加装Hexapod 六自由度调整装置，根据望远镜俯仰角度变化采用实时查表补偿次镜的位置，补偿量可以通过有限元模型分析或者外场观星标定得出。然而，有限元分析对这种复杂模型简化边界条件，结果过于理想化，外场观星标定的方法综合影响星象像差和指向变化的所有因素，最终次镜补偿虽能取得一定效果，但达不到最优效果。因此，通过直接精确测量分离出主次镜弯沉误差，然后反馈给次镜Hexapod 调整机构补偿［7］，之后再通过外场恒星标定补偿其他因素引起的指向误差效果会更佳。

激光跟踪仪等坐标测量手段可以测量大尺寸零部件的几何位置误差，但对于大口径望远镜主次镜弯沉的检测需要多站或者转站完成，测量操作复杂，精度难以保证，而且效率低。

本文针对大口径望远镜系统的结构特点，提出了结合光学和图像处理的主次镜弯沉误差直接测量方法，该方法测量精度高，操作方便。

2 主次镜位姿影响因素分析

本文所述的大口径望远镜结构如图1 所示。其中，镜筒包括主镜室组件、次镜组件、环梁、桁架结构及四通等，总长度约为8 m，宽5.6 m，总质量接近30 t。四通是整个镜筒与跟踪架连接的枢纽，因此四通是一个刚度较好的大型结构件［8-9］。主镜室安装在四通一侧，主镜采用主动光学支撑机构，通过底支撑与侧支撑机构安装在主镜室内，主镜室安装多个轴向及径向测微仪，通过促动器实时调整，保证主镜相对于主镜室姿态固定不动。次镜组件通过桁架结构连接在四通的另一侧，次镜组件采用Hexapod平台调整次镜姿态，Hexapod 平台的相关参数见表1。

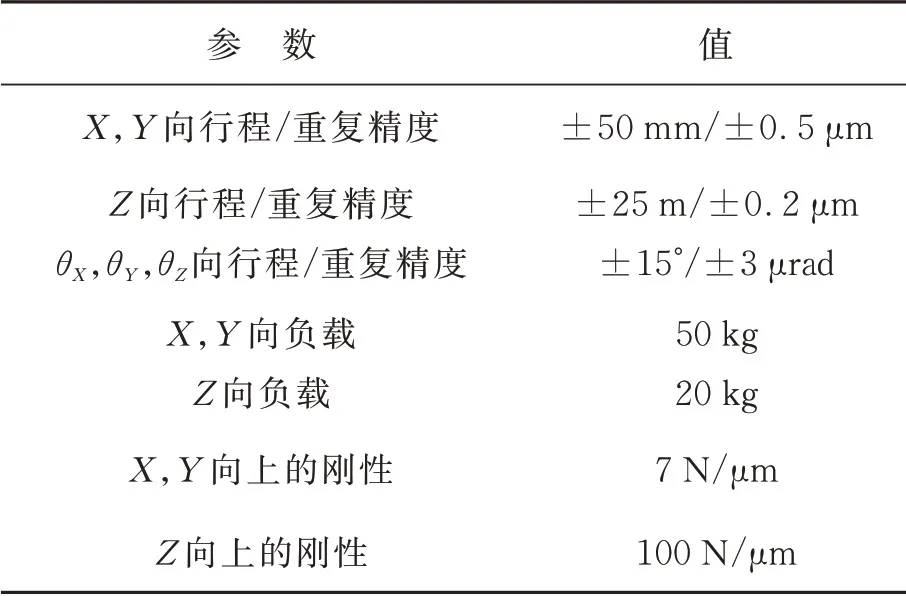
表1 Hexapod 的具体参数Tab.1 Specifications of Hexapod

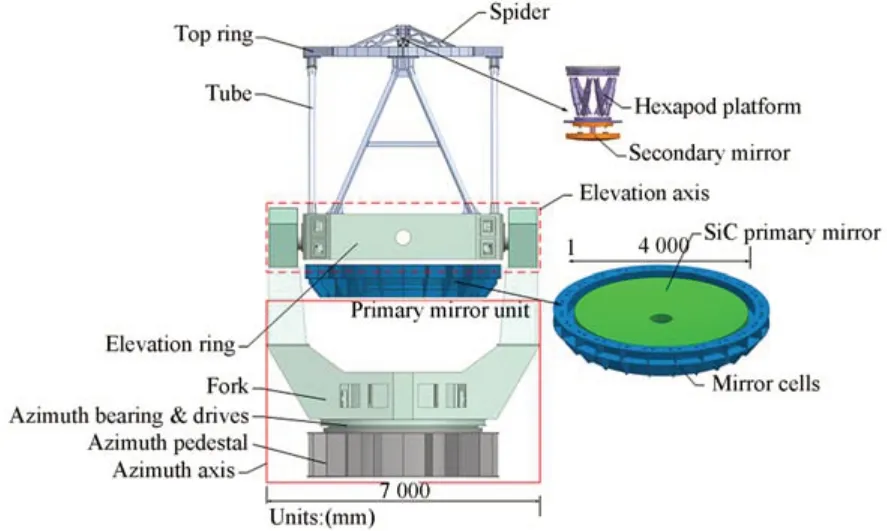
图1 大口径望远镜结构Fig. 1 Structure of large-aperture telescope

造成主次镜位姿变化的主要因素如下：（1）主镜室结构受重力变形引起主镜M1 在主镜室内串动；（2）次镜Hexapod 平台自身刚度导致的次镜弯沉；（3）桁架变形引起的次镜端偏移，整个次镜支撑结构及环梁质量达到了2 t，桁架的八根杆连接次镜环梁和四通，重力引起的桁架形变量是引起次镜环梁偏移的主要原因；（4）四通结构刚度各向不一致引起的变形，四通承载主次镜所有支撑结构的质量，相当于受动载荷的简支梁结构，镜筒垂直和水平状态四通的变形是不一样的；（5）温度变化导致所有结构件伸缩带来的主次镜位置变化。

望远镜主光学系统理论设计的最佳状态如下：（1）次镜相对主镜位置应固定不动，保证成像质量；（2）主镜与粗跟踪光轴固定不动，保证指向精度。但四通及主镜室都非绝对刚体，这种变形导致主镜光轴与粗跟踪光轴不再平行，只影响指向精度。以主镜为基准，次镜相对主镜有6 个运动自由度，其中绕光轴的旋转对于同轴光轴系统的影响可忽略，主次镜的间距主要引起离焦误差，可以根据像点来修正。其他4 个自由度包括二维径向偏移和二维角度偏转，统称为次镜的弯沉误差，如图2 所示。

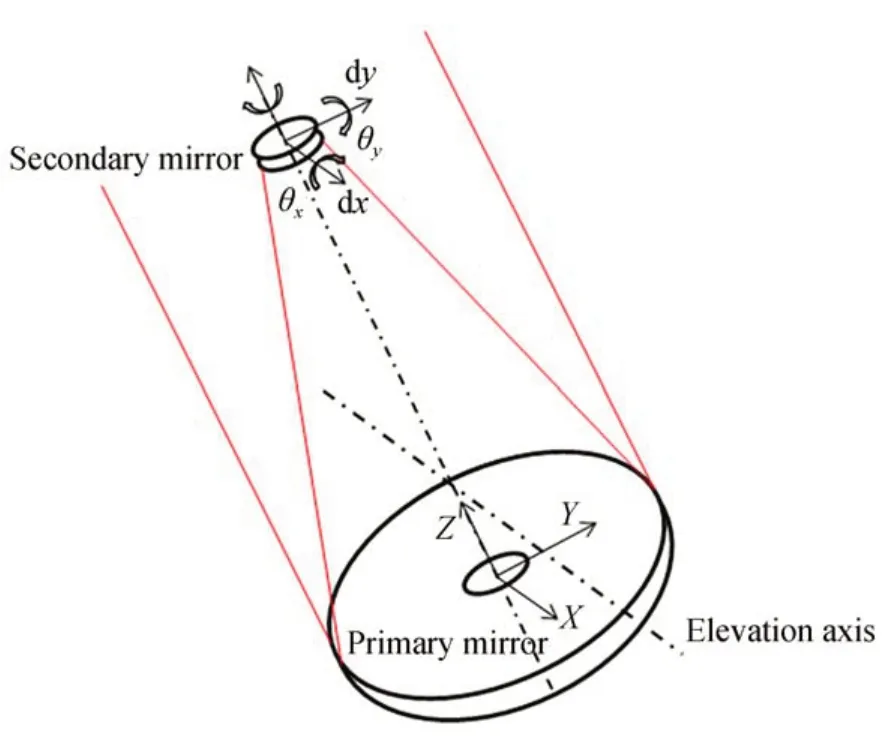
图2 主次镜弯沉误差示意图Fig.2 Schematic diagram of deflection error of primary and secondary mirrors

为了精确测量分离出主次镜之间的相对弯沉误差，并通过Hexapod 平台调整次镜进行修正，本文在保证光学像质的同时修正部分的光轴指向误差，再通过外场恒星标定法，利用卡式光学系统零彗差点理论去掉其他光轴的指向误差。

3 测量原理及方法

本文设计了次镜相对主镜的弯沉误差测量装置，如图3 所示。该装置包括内调焦光管、光管安装调整机构、平面反射镜和次镜端探测器。内调焦光管由固定透镜组、调焦透镜组、分光镜、光纤点光源及光管探测器组成［10］。光纤点光源连接在内调焦光管后端的焦点位置，光管探测器安装在内调焦光管的侧面经分光镜转折形成的分光焦点位置。

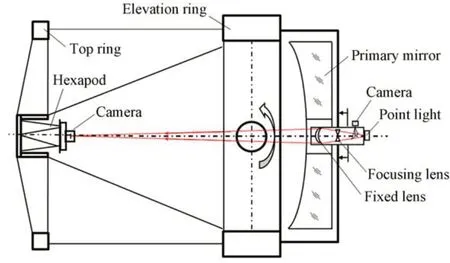
图3 主次镜径向偏移测量原理Fig.3 Measuring principle of radial offset of primary and secondary mirrors

内调焦光管是一种特制的专用光学测量装置，通过调节调焦透镜组沿光轴方向移动，可以把光纤点光源投射成像在300 mm 至无穷远位置。因此，利用内调焦光管可实现径向偏移和角度偏移两种测量模式。

3.1 径向偏移测量模式

测量次镜径向偏移时，以内调焦光管光轴为基准，利用光轴的直线性不随重力场变化的特性，光管投射光斑至次镜附近，通过次镜位置安装的探测器测量光斑脱靶量得到次镜的径向偏移误差。测量前安装内调焦光管于主镜中孔，安装次镜端探测器于次镜位置，调整内调焦光管与主镜光轴大致同轴，利用Heaxpod 调整次镜端探测器的位置，使它能够接收光纤点光源的像点，微调内调焦光管调焦透镜组的位置，使像点光斑最小。然后，把望远镜光轴水平位置作为测量起始状态，仔细调整内调焦光管及次镜端探测器位置，使光纤像点成像在次镜端探测器的合适位置，锁紧调整机构。记录次镜端探测器水平及垂直两个方向的脱靶量，然后望远镜俯仰轴带动主次镜镜筒旋转，记录在不同俯仰角θ下次镜端探测器水平及垂直两个方向的脱靶量dxθ，dyθ。

3.2 角度偏转测量模式

测量次镜角度偏转时，内调焦光管切换到自准值模式，相当于光学自准直仪，光管与主镜固定在一起，通过测量次镜位置的平面镜角度变化得到次镜相对主镜的角度偏转。

首先，移除次镜端探测器，安装固定好平面反射镜，调整内调焦光管调焦透镜组的位置，使内调焦光管发射平行光。然后，利用Hexapod 调整平面反射镜的角度，使平行光原路返回进入内调焦光管并在光管探测器上成像，再重复调整调焦透镜组的位置，使像点光斑最小，如图4 所示。

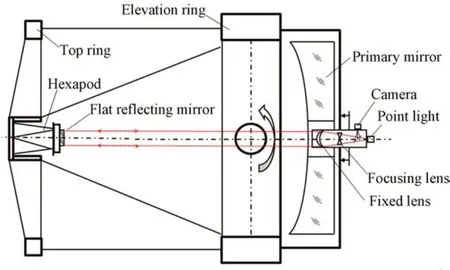
图4 主次镜角度偏转测量原理Fig.4 Measuring principle of angle deflection of primary and secondary mirrors

把望远镜的光轴水平位置作为测量起始状态，仔细调整内调焦光管及平面反射镜位置，使光纤像点自准直成像在光管探测器的合适位置，锁紧调整机构。记录光管探测器水平及垂直两个方向的脱靶量，然后望远镜俯仰轴带动主次镜镜筒旋转，记录在不同俯仰角θ下次镜端探测器水平及垂直两个方向的脱靶量mθ，nθ。

最后，根据光管探测器两个方向的脱靶量mθ，nθ计算出平面反射镜两个方向的角度偏转rxθ，ryθ，即：

其中f为内调焦光管发射平行光状态时的焦距。

4 实验与结果分析

对某望远镜主次镜弯沉进行测量，首先移除次镜组件，为了保证测量准确，Heaxpod 平台上安装次镜组件等重的配重板。主次镜间距5.5 m，光纤点光源激光器波长为632.8 nm，光纤芯径为单模4 μm，CCD 探测器像元尺寸为2.9 μm，靶面尺寸为1 920×1 080，内调焦光管口径为50 mm，发射平行光状态时光管焦距为300 mm。

4.1 径向偏移测量

在主镜中孔位置安装固定内调焦光管，次镜六自由度平台安装CCD 探测器，通过调焦把激光点光源投射到CCD 靶面成像清晰，如图5 所示。旋转俯仰轴，测量光点在CCD 上的变化量，俯仰角每5°测试一次数据，来回共两次，数据见表2。

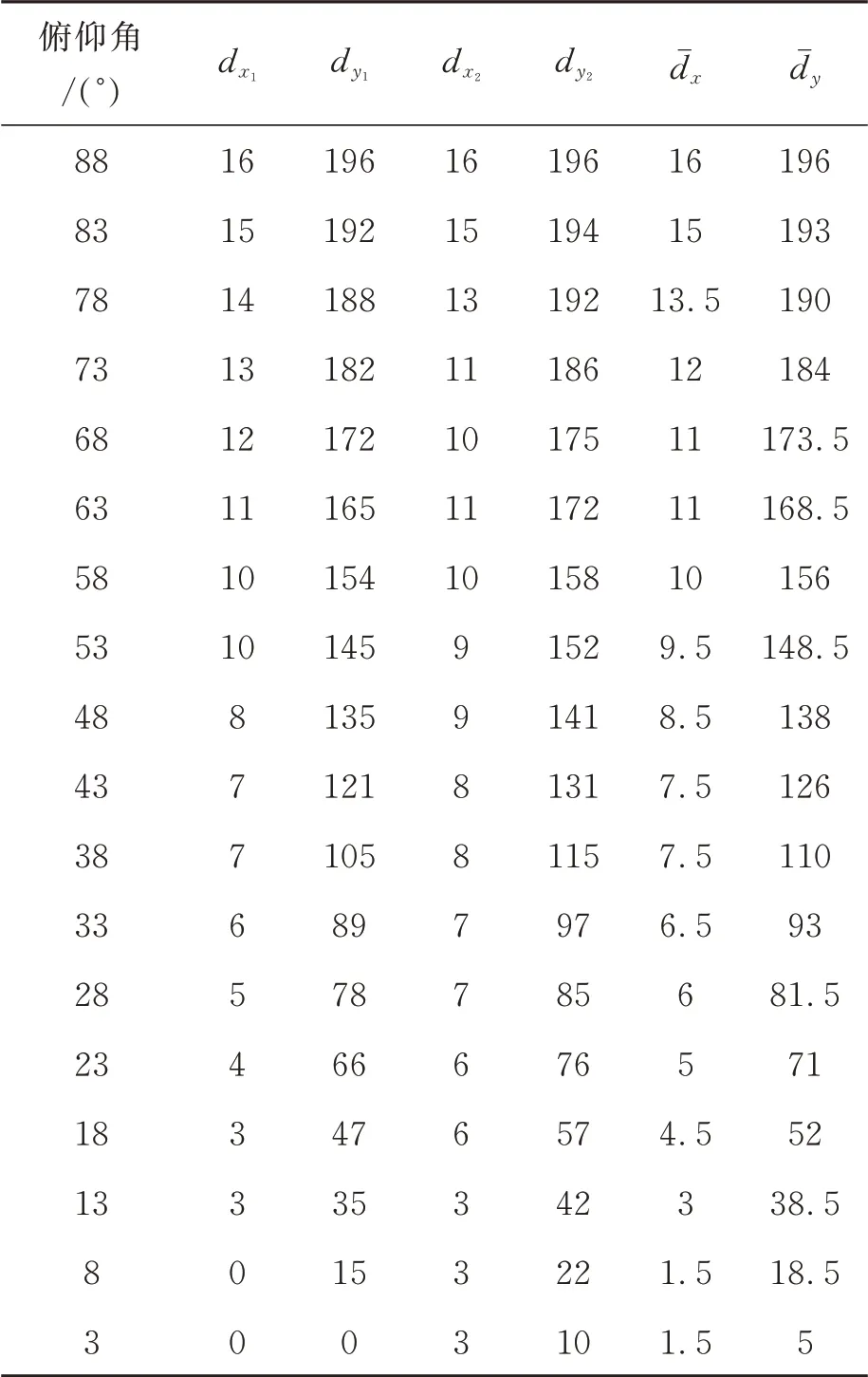
表2 位置偏移测试数据Tab.2 Position offset test data （μm）

图5 径向偏移测量Fig.5 Radial displacement measurement

4.2 角度偏转测量

移除次镜六自由度平台CCD 探测器，安装固定平面镜，调节内调焦光管，使其发射平行光。然后调整平面反射镜的角度，使平行光原路返回进入内调焦光管并在光管探测器上成像，再重复调整调焦透镜组的位置，使像点光斑最小。旋转俯仰轴，测量光点在光管探测器上的变化量，俯仰角每5°测试一次数据，来回共两次，数据见表3。

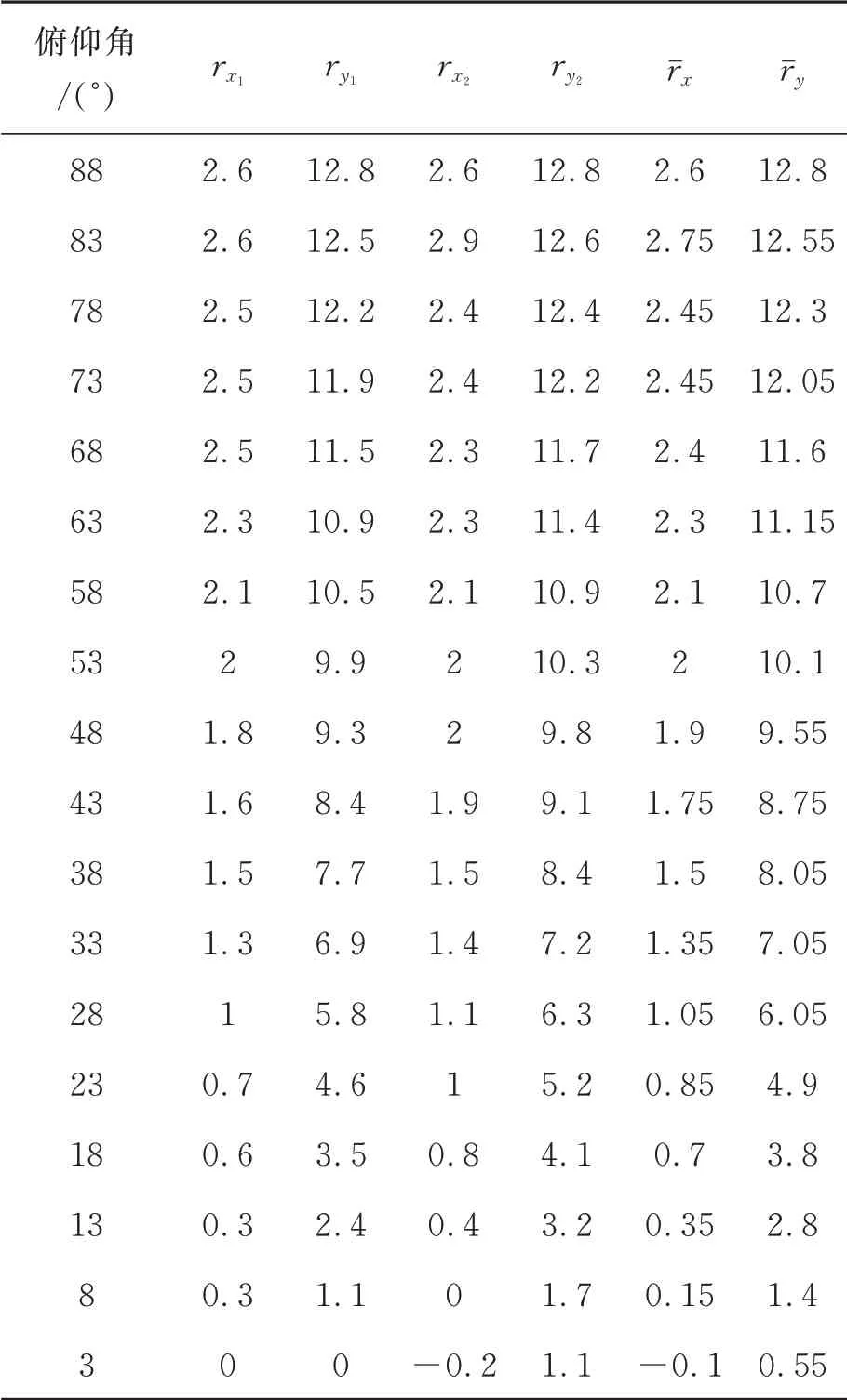
表3 角度偏转测试数据Tab.3 Angular deflection test data （″）

4.3 测量结果分析

从测量结果可以看出：水平方向弯沉误差较小，垂直方向弯沉误差变化大，如图6 所示。这符合实际情况，水平方向不受重力场影响，而且镜筒结构沿光轴方向对称，理论上水平方向的弯沉误差应该为零，但加工误差及装配应力导致结构刚度水平方向不能完全对称，尤其是桁架及Heaxpod 平台。

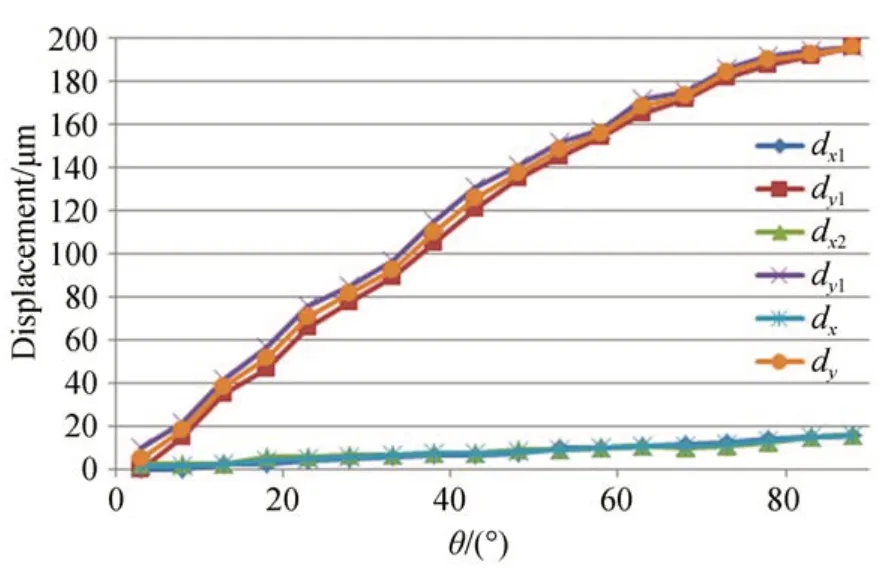
图6 主次镜位置偏移曲线Fig.6 Position offset curves of primary and secondary mirrors

径向偏移误差较大，最大为196 μm，而角度偏转误差较小，为12.8″，如图7 所示。

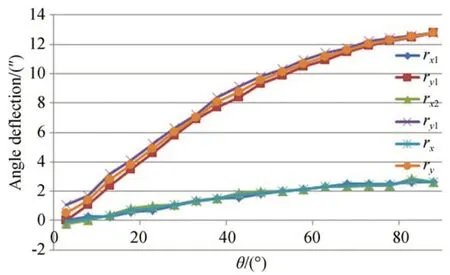
图7 主次镜角度偏转曲线Fig.7 Angle deflection curves of primary and secondary mirrors

5 有限元分析

对本文测量的某望远镜主次镜弯沉进行有限元分析，模型如图8 所示。根据实际受力情况，约束镜筒两侧轴头，对镜筒施加重力载荷，分析镜筒光轴从竖直到水平状态主次镜位置的相对变化，主次镜光学镜体可以看成刚体。结果表明，次镜相对主镜的径向偏移最大为0.17 mm，测量结果偏大26 μm，水平方向的径向偏移基本为零。次镜相对主镜的角度偏转最大为9.6″，测量结果偏大3.2″，水平方向的角度偏转也基本为零。分析结果比测量结果稍小，这是由于实际结构由于加工及装配应力的存在，受力变形并非理想状态，镜筒为轴对称结构，有限元分析不产生水平方向的形变。因此，实际测量结果更能真实反映主次镜的弯沉情况。

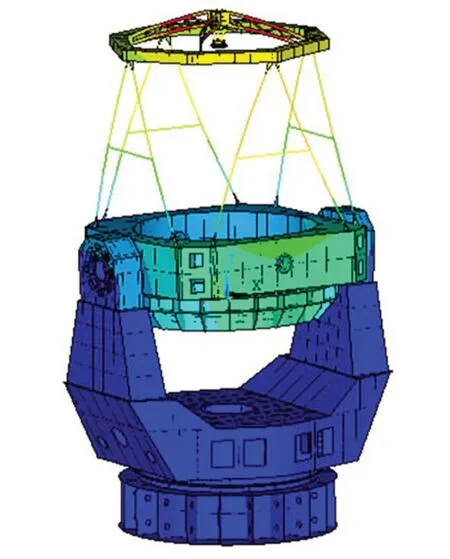
图8 大口径望远镜的有限元分析模型Fig.8 Finite element analysis model of large-aperture telescope

主次镜相对角度的偏转误差分析及实测结果都较小，这是由于桁架及Heaxpod 平台结构自身的特点，杆件闭环机构能够很好地补偿顶部的角度扭转。

6 测量不确定度分析

6.1 径向偏移测量不确定度

径向偏移测量的不确定度影响因素主要有：CCD 探测器像点质心提取精度引起的不确定度u1，内调焦光管光轴晃动引起的不确定度u2，内调焦光管及安装调整结构刚度引起的不确定度u3，以及温度及气流引起的不确定度u4。其中，u1可以统计分析，用实验标准误差来表征，故采用A类评定；u2，u3，u4不可以用统计学方法计算，根据经验估计取值，采用B 类评定方法［11］。

6.1.1 CCD 探测器像点质心提取精度引起的不确定度

微调光管使像点成像最好，CCD 探测器提取质心多次重复测量，记录测量数值，计算其标准差为0.004 mm，则u1=0.004 mm。

6.1.2 内调焦光管光轴晃动引起的不确定度

内调焦镜组机构设计锁定较好，光学设计分析调焦镜组晃动量影响光轴偏心最大为0.02 mm，取u2=0.02/3=0.006 mm。

6.1.3 内调焦光管及安装调整结构刚度引起的不确定度

结构刚度在变化重力场中引起的光管角度偏转对测量的影响最大，光管及安装调整结构设计过程中严格保证并通过有限元分析，角度偏转α最大控制在0.5″，光管距探测器d=5.5 m，故u3=αd/3=0.000 46 mm。

6.1.4 温度及气流引起的不确定度

整个测量过程小于5 min，在装调大厅测量环境条件下，保持整个系统不动，记录探测器测量值在5 min 内变化的最大值为0.009 mm，则u4=0.009/3=0.003 mm。

各项误差引起的不确定度分量相互独立，则相关系数为零，径向偏移测量的合成标准不确定度为：

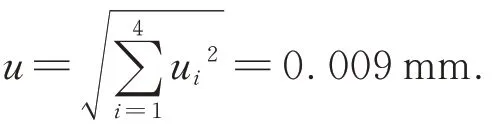
6.2 角度偏转测量不确定度

角度偏转测量的不确定度影响因素主要有：光管探测器像点质心提取精度引起的不确定度u1，内调焦光管调焦误差引起的不确定度u2，内调焦光管光轴晃动引起的不确定度u3，内调焦光管及安装调整结构刚度引起的不确定度u4，光管焦距测量不准确引起的不确定度u5，以及温度及气流引起的不确定度u6。其中，u1，u2可以统计分析，用实验标准误差来表征，故采用A 类评定；u3，u4，u5，u6不能用统计分析计算，根据经验估计取值，采用B 类评定方法。

6.2.1 光管探测器像点质心提取精度引起的不确定度

微调光管使像点成像最好，光管探测器提取质心多次重复测量，记录测量数值，计算其标准差为0.1″，则u1=0.1″。

6.2.2 内调焦光管调焦误差引起的不确定度

先固定位置，多次重新调节内调焦光管使像点重新聚焦，记录各次测量的数值，计算其标准差为0.2″，则u2=0.2″。

6.2.3 内调焦光管光轴晃动引起的不确定度

内调焦镜组机构设计锁定较好，光学设计分析调焦镜组晃动量影响角度测量误差最大为0.3″，取u3=0.3/3=0.1″。

6.2.4 内调焦光管及安装调整结构刚度引起的不确定度

结构刚度在变化重力场中引起的光管角度偏转对测量影响是直接的，光管及安装调整结构设计过程中严格保证并通过有限元分析，角度偏转最大控制在0.5″，故u4=0.5″。

6.2.5 光管焦距测量不准确引起的不确定度

内调焦光管经过高精度多齿分度台标定，测量范围内最大误差为1″，则u5=1/3=0.33″。

6.2.6 温度及气流引起不确定度

整个测量过程小于5 min，在装调大厅测量环境条件下，保持整个系统不动，记录探测器测量值在5 min 内变化的最大值为0.3″，则u6=0.3/3=0.1″。

各项误差引起的不确定度分量相互独立，则相关系数为零，测量径向偏移的合成标准不确定度为：

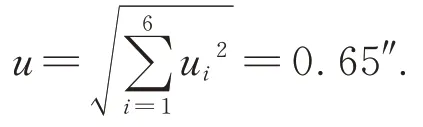
7 结 论

本文针对大口径望远镜主次镜弯沉测量的特点，提出一种利用内调焦光管结合平面镜和探测器的基于光学及图像处理的测量方法，分析了该方法的基本原理，并对一间距为5.5 m 的主次镜进行弯沉的精确测量，测得水平方向的径向偏移最大为196 μm，垂直方向的径向偏移最大为16 μm，水平方向的角度偏转最大为2.6″，垂直方向的角度偏转最大为12.8″。测量结果的重复性较好。最后对该方法的测量不确定度进行分析，测量径向偏移的合成标准不确定度为9 μm，测量角度偏转的合成标准不确定度为0.65″。该方法测量精度高，满足大口径望远镜光学系统的对准精度要求。