大口径望远镜中间体拓扑优化及形位公差检测

王志臣，陈 涛，曹玉岩，2，周 超

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049）

1 引 言

望远镜是人类认识太空、探索宇宙的重要工具，随着探索的不断深入，科学家希望看得越来越远，看得越来越清晰，望远镜的口径也越来越大。随着口径的增大，望远镜中间体的结构尺寸、质量和惯量随之增大，对中间体的设计和检测提出挑战。

中间体是望远镜光学系统的承载体，下方安装主镜组件，上方安装次镜组件，左右两侧连接俯仰轴承，实现俯仰0～90°的转动，其性能优劣直接影响望远镜光学系统的稳定和指向精度。中间体的性能主要体现在两方面，一是高刚度、低惯量，刚度直接影响主、次镜相对位置的稳定，质量和惯量则影响望远镜的伺服性能，尤其是大口径望远镜影响更为明显［1-3］。二是形位公差精度，望远镜俯仰轴承的同轴由中间体两侧轴孔的同轴度和轴孔端面平行度保证，俯仰轴为简支回转结构，两端轴承的回转轴应在同一直线上，否则将影响望远镜的指向和跟踪精度。

口径较小的望远镜，一般根据传统经验和参数优化即可完成中间体的设计，质量和惯量在可接受范围内，尚无严格要求，中间体的形位公差可利用三坐标测量仪检测。但随着大口径望远镜结构尺寸的增大，中间体的质量和惯量成倍增加，传统经验和参数优化设计已无法满足中间体高刚度、低惯量的设计需求，与此同时，中间体的尺寸已超出大多数三坐标测量仪的量程，三坐标测量仪难以对其形位公差进行测量。

拓扑优化方法随着有限元理论和优化准则法的发展而日益成熟，应用在结构设计初期，优化空间大，更容易得到形状合理、布局紧凑的轻量化构型。近些年，拓扑优化逐步应用在望远镜结构设计中，且取得了丰硕的成果，尤其是在主镜支撑方面［4-6］。Park 等采用拓扑优化方法完成了φ566 mm 反射镜的设计，轻量化率为78%［7］。刘书田等采用拓扑优化方法完成φ2 m 空间反射镜的优化和设计，轻量化率达到86%［8］。

大尺寸中间体形位公差的检测是加工过程中的一个难题，机床打表法依赖机床导轨的精度，且存在刀杆随伸长量增加逐渐弯沉的问题；测微准直望远镜法操作过程繁琐，引入的操作误差较大，检测精度不高。光学检测法不受尺寸和距离的限制，本文利用自准直仪测角实现中间体轴孔端面平行度误差的测量，利用激光跟踪仪空间点坐标的测量实现中间体轴孔同轴度误差的测量。

2 中间体结构设计

2.1 拓扑优化理论

拓扑优化是在给定设计空间寻找最优形状和材料布局的数学算法，应用于结构设计的初始阶段，可以依据承载要求和约束条件得出合理的结构布局，为结构优化和设计提供指导［9］。

常用的拓扑优化方法有变密度法、变厚度法和均匀化法。其中，变密度法是应用较为广泛的一种方法，具有变量少、计算效率高、容易实现等优点［10-11］。本文采用变密度法中较为成熟的固体各向同性材料惩罚模型（SIMP），模型中单元的相对密度连续可变（ρi∈[0，1]），材料属性与相对密度的关系为：

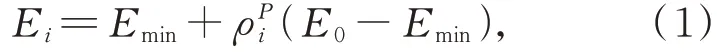
式中：Ei为第i个单元相对密度ρi对应的弹性模量，E0为相对密度为1 对应的弹性模量，Emin为单元相对密度为ρmin对应的弹性模量，p为惩罚因子。以应变能最小为优化目标，形变位移和质量为约束，优化目标函数可表示为：

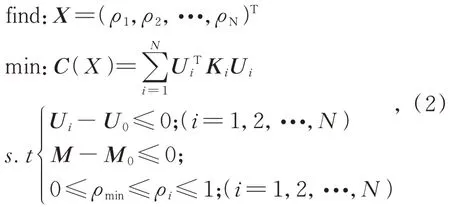
式中：单元相对密度X=（ρ1，ρ2，…，ρN）T为优化设计变量，总应变能C（x）最小为优化目标，Ki=K0为单元刚度矩阵，U0为约束的最大形变位移，M0为约束的最大质量。

优化准则法通过构造拉格朗日函数将有约束的优化问题转变为无约束的极值问题，具有迭代次数少、收敛速度快的优点，构造函数为：

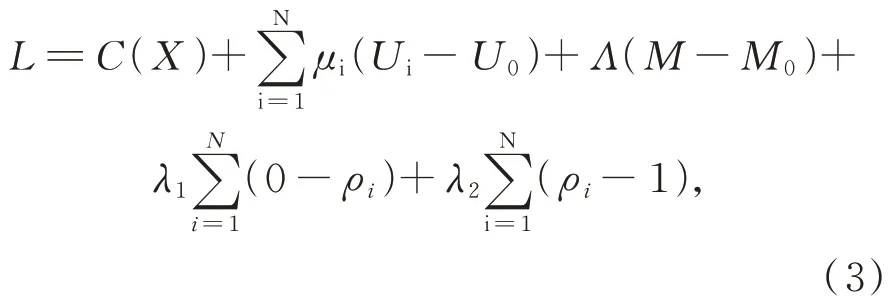
式中：μi（i=1，2，…，N），Λ，λ1，λ2分别为形变位移、质量和密度上下限约束的拉格朗日乘子。最优解必须满足Kuhn-Tucker 条件，才能进行灵敏度计算。

目标函数C（x）关于ρi的灵敏度为：

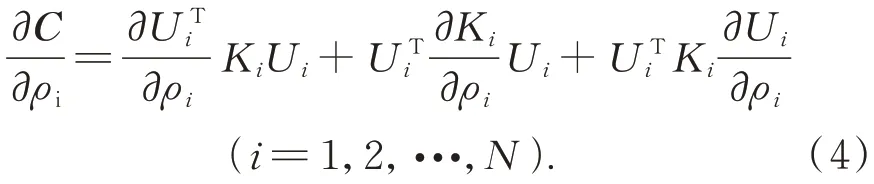
单元刚度Ki=ρP i K0对ρi求偏导：

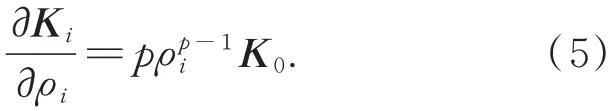
位移矩阵KU=P对ρi求偏导：

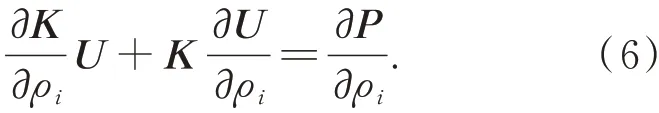
载荷P与单元相对密度ρi无关，由上式得形变位移关于ρi的灵敏度：

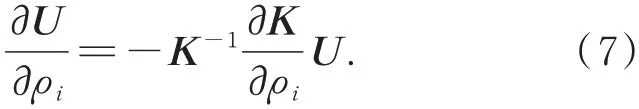
将式（5）和式（7）代入式（4）得应变能关于ρi的灵敏度：

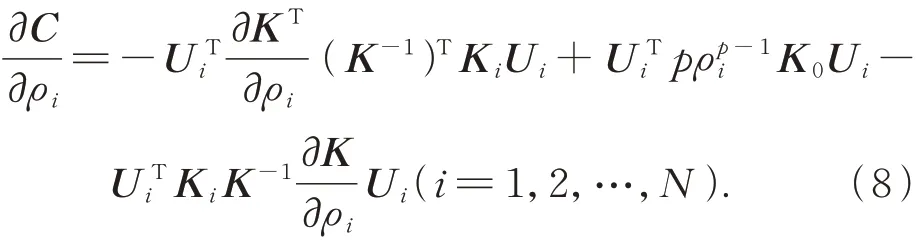
质量M=ρim0(i=1，2，…，N)关于ρi的灵敏度：

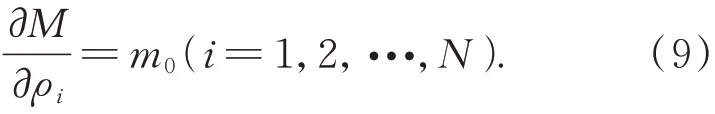
在完成目标函数和约束关于设计变量的灵敏度分析后，采用优化准则法更新设计变量至优化结束，中间体设计流程如图1 所示。

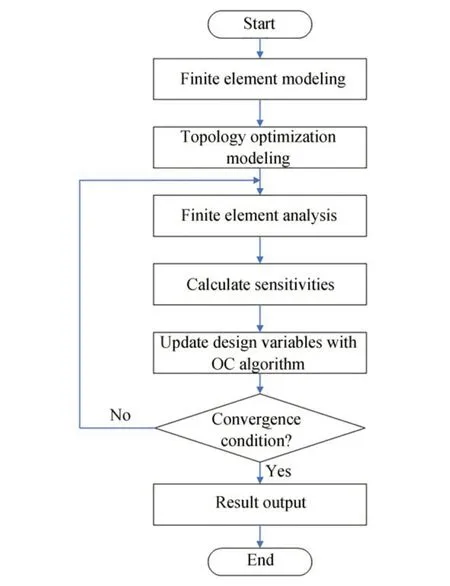
图1 中间体设计流程Fig.1 Design flowchart of center section

2.2 中间体拓扑优化

中间体边界载荷有主镜组件、次镜组件和自身重力载荷，中间体由左、右轴支撑。将主镜组件、次镜组件等效为集中力，建立有限元模型如图2 所示。

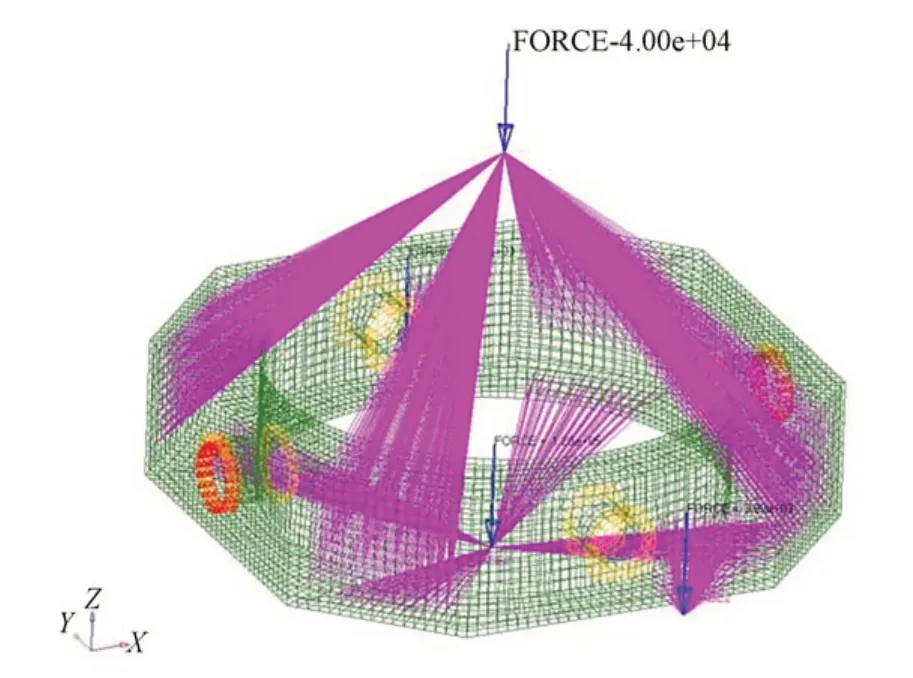
图2 中间体等效载荷的有限元模型Fig.2 Finite element model of center section with equivalent load

根据工况确定中间体的非优化区域和优化区域，根据上节拓扑优化数学模型，设定参数见表1。应用上述参数，拓扑优化迭代结果如图3所示。挖空区域表示目标函数关于该区域单元的灵敏度较小，保留区域颜色深浅表示材料密度不同，颜色越深表示目标函数关于该区域单元的灵敏度越大，应予保留。

表1 中间体拓扑优化模型参数Tab.1 Parameters of topology optimization for center section

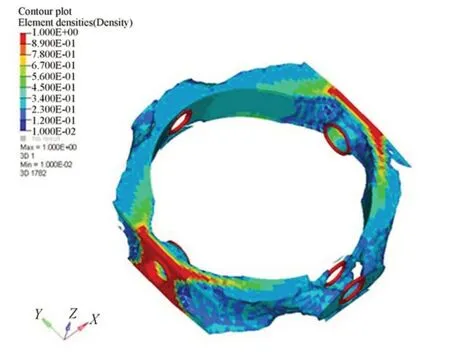
图3 中间体拓扑云图Fig.3 Topology optimization contour of center section

2.3 中间体结构再设计

根据拓扑优化结果，结合生产工艺对中间体的壁厚、筋的排布进行再设计，结构变形如图4 所示。相比于传统经验设计的中间体，质量由13 t减轻为10.2 t，减少21.5%，最大变形由0.21 mm减小为0.18 mm，静态刚度提高14.3%。

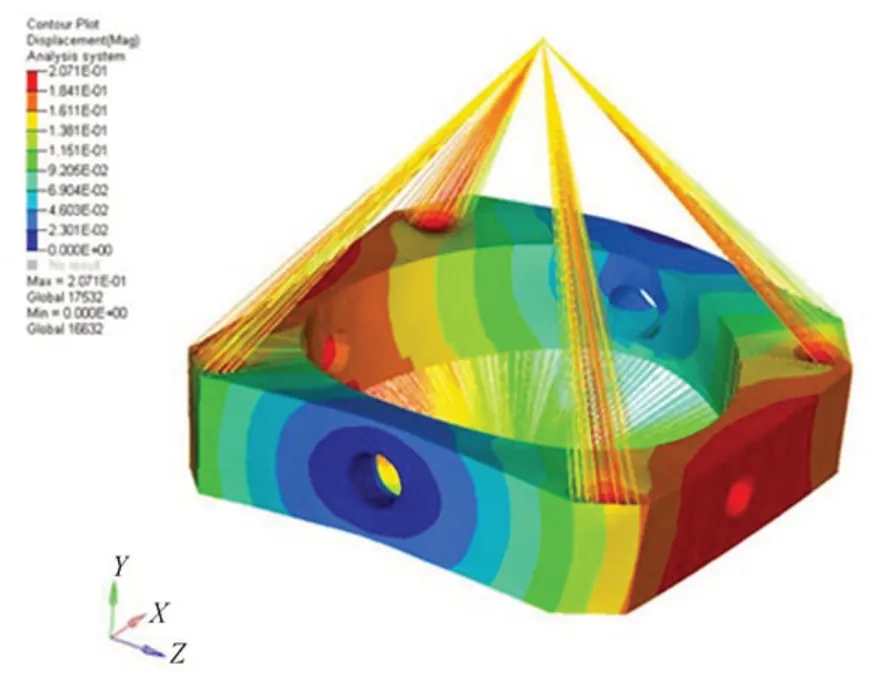
图4 中间体结构变形云图Fig.4 Deformation contour of center section

3 中间体形位公差检测

3.1 中间体的形位公差

望远镜俯仰轴为两侧简支结构，即左、右两侧为支撑轴承，要保证望远镜的指向准确，左、右两侧轴承的回转轴必须一致。中间体是左、右轴承的连接体，由中间体两侧轴孔定位左、右轴承的回转轴位置，中间体两侧轴孔端面的平行度误差决定左、右轴承回转轴的角度偏差，中间体两侧轴孔的同轴度误差决定左、右轴承回转轴的位置偏差。对于尺寸较小的中间体，可在三坐标测量仪上测量轴孔同轴度和轴孔端面平行度误差；对于大尺寸中间体，则很难找到适用的三坐标测量仪，而机床打表法和测微准直望远镜法容易引入操作误差，检测精度有限。

3.2 中间体平行度误差检测

自准直仪利用光的自准直原理实现角度测量，且与测量距离无关。如图5 所示，Z向沿轴线指向自准直仪，Y向竖直向上，X向由右手定则确定，将装有平面反射镜的工装沿Y向吸附在中间体右侧轴孔端面，自准直仪读数为θ1，工装上下调转180°，自准直仪读数为θ2，保持自准直仪位置不动，将工装沿Y向吸附在中间体左侧轴孔端面，自准直仪读数为θ3，工装上下调转180°，自准直仪读数为θ4。

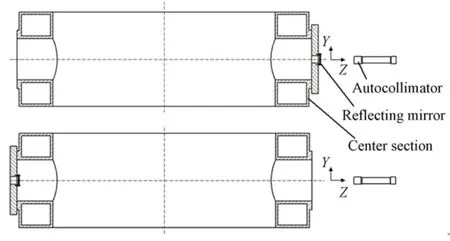
图5 平行度误差检测原理Fig.5 Detection principle of parallelism errors

图5 中，平行度误差测量时利用工装的不同吸附面，假设平面反射镜与工装吸附面存在Y向夹角偏差α，自准直仪与轴孔端面Y向垂直度误差θR，工装翻转180°可消除夹角偏差α，即：

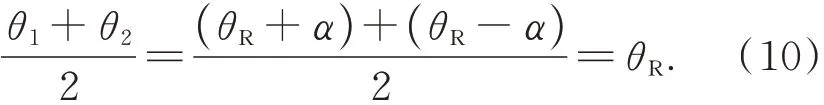
故工装两吸附面无平行度要求，且不会对测量结果产生影响，中间体轴孔端面Y向平行度误差为：

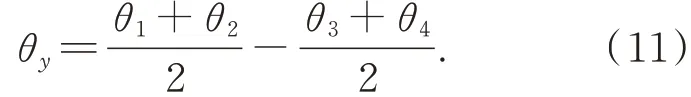
同理，将工装沿X向吸附，可得出中间体轴孔端面X向平行度误差θX。采用分辨力为0.1″的数显测微自准直仪完成中间体轴孔端面平行度误差检测，如图6 所示，两侧轴孔端面X向角度偏差为5.1″，Y向角度偏差为0.7″，由端面直径得出轴孔端面平行度误差为0.016 mm。

图6 中间体平行度误差检测Fig.6 Detection of parallelism error for center section

3.3 中间体同轴度误差检测

激光跟踪仪利用角反射器实现空间点坐标的测量，如图7 所示，在中间体轴孔端面建立测量坐标系，Z向沿轴线指向中间体，Y向竖直向上，X向由右手定则确定。使用两块千分表分别测量轴孔和端面的跳动，调整回转工装与中间体左侧轴孔同轴，靶球随工装转动，激光跟踪仪测量靶球转动过程中的多个位置（xi，yi，zi），令：

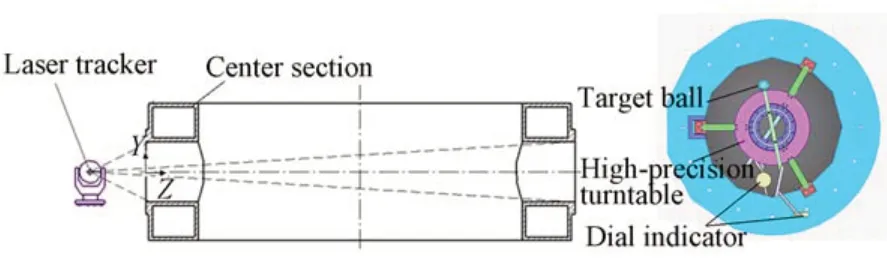
图7 同轴度误差检测原理Fig.7 Detection principle of coaxiality error

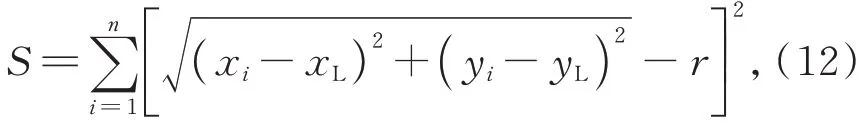
式中：（xL，yL）为左侧拟合圆心坐标，r为拟合圆心半径，n为采样点个数。由最小二乘法求得轴孔圆心在测量坐标系中的位置（xL，yL），同理拟合求解右侧轴孔圆心的位置（xR，yR），则中间体轴孔圆心位置误差为：

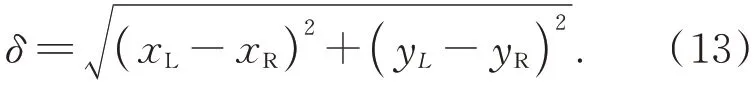
采用Leica AT402 完成中间体轴孔同轴度误差检测，如图8 所示，由式（13）得出两侧轴孔圆心位置偏差为0.03 mm。

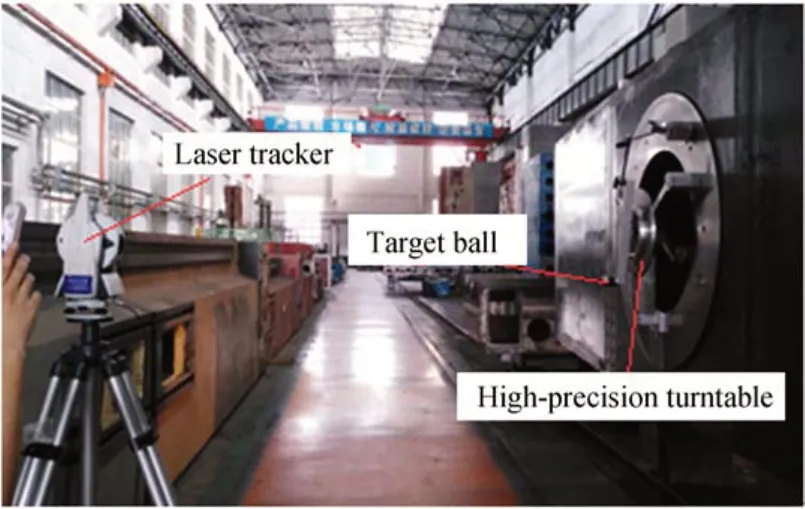
图8 中间体同轴度误差检测Fig.8 Detection of coaxiality error for center section

4 结 论

本文开展了基于拓扑优化的大口径望远镜中间体结构设计，以应变能最小为优化目标，形变位移和质量为约束，分析应变能的灵敏度，得出拓扑优化结果并以此为指导，结合实际应用完成中间体结构设计，其质量为10.2 t，最大变形为0.18 mm，相比于传统经验设计的中间体，质量减轻21.5%，静态刚度提高14.3%。然后，提出基于自准直仪和激光跟踪仪检测中间体形位公差的光学检测法，并完成中间体的检测，中间体轴孔端面平行度误差为0.016 mm，轴孔圆心位置偏差为0.03 mm，解决了加工过程中大尺寸中间体的检测难题。