地基大口径望远镜动态目标跟踪中压电式快速反射镜迟滞效应的补偿

刘永凯，吕福睿，高世杰，邓永停，吴 昊

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049）

1 引 言

随着探测能力、空间分辨率等的提高，地基大口径望远镜对伺服系统跟踪性能的要求越来越高。系统结构多为复合轴跟踪结构，以动态范围广的主轴作为粗跟踪系统，以响应速度快的子轴作为精跟踪系统。而精跟踪控制系统的带宽越高，复合轴系统的动态目标跟踪能力越强，稳定性越高。研究结果证明，为充分发挥复合轴系统的优势，精跟踪系统的闭环带宽应是粗跟踪系统闭环带宽的6～10 倍［1］。因此，精跟踪系统带宽对于地基大口径望远镜的动态目标跟踪性能至关重要。

压电促动器（Piezoelectric Actuator ，PEA）具有尺寸小、质量轻、出力大、噪声低等优点，而且具备纳米级的分辨率、超高的重复定位精度和优异的动态特性，因此在精密制造、生物医疗、半导体产业、航空航天、自动化与机器人技术、消费电子和精密光学等领域得到了广泛应用［2］。压电式快速反射镜以PEA 为驱动元件，具有响应速度快、指向精度高、谐振特性好、抗电磁干扰能力强等优点，广泛应用在自适应光学［3］、激光通信［4］、光束准直［5］和三维显微镜［6］等系统中，以实现光束的高精度指向与精密跟踪。然而，PEA 材料的固有特性决定了压电式快速反射镜必然会存在迟滞非线性效应［7-10］，这不仅会导致系统控制精度的降低，还会在闭环跟踪的过程中导致系统有效带宽的下降，严重影响光电系统的动态目标跟踪能力。因此，对压电式快速反射镜的迟滞效应进行补偿控制，是提高精跟踪系统带宽，实现高性能动态目标跟踪的关键。

目前，描述PEA 迟滞的模型主要包括：Preisach 模 型［11］、Prandtl-Ishlinskii（P-I）模 型［12］、Krasonselskii-Pokrovskii（K-P）模 型［13］、分 数 阶 模型［14］和Bouc-Wen 模型［15］等。上述模型均为静态模型，随着PEA 控制信号变化频率的提升，模型精度下降，因此人们针对PEA 动作频率与迟滞效应的关系开展研究，提出了基于Hammerstein结构的率相关迟滞模型［16］。

在压电式快速反射镜控制方面，常见的控制方法主要有前馈控制、反馈控制和前馈-反馈复合控制等。袁刚［17］采用基于Bouc-Wen 模型的前馈控制法，使压电式快速反射镜的镜面偏转角度与输入控制电压的线性度提高到2.3%，迟滞误差减小到±0.5%，该控制方式属于开环控制，并未研究闭环系统的跟踪带宽。王昱棠［18］采用双PID 闭环的反馈控制方法，在频率为30 Hz 的跟踪信号下跟踪残差相比于单环控制降低46%，由于该方法通过内部闭环来改善迟滞非线性，降低了系统的响应速度和带宽。王玉坤［19］提 出 采 用Smith 预 估 算 法 补 偿PID 的 闭 环控制方式，系统误差抑制带宽较传统PID 控制提高26%，但该方式将迟滞非线性扰动作线性处理，没有进行补偿，因此系统的动态性能还可进一步提高。

根据研究现状可知，针对率相关迟滞前馈补偿法对闭环跟踪系统带宽影响的研究相对较少。然而，在基于地基大口径望远镜的复合轴光学目标动态跟踪系统中，以压电式快速反射镜为执行机构的精跟踪系统主要抑制的是中高频段的扰动，其系统带宽对于整个系统的目标跟踪性能至关重要。针对上述问题，本文从提高系统动态目标跟踪性能的角度出发，基于应用广泛、模型可靠的P-I 模型结合动态线性ARX 模型建立了压电式快速反射镜的率相关动态迟滞模型，并结合反馈控制算法进行复合控制，以提高基于压电式快速反射镜的精跟踪系统误差抑制带宽，进而提高复合轴系统的动态目标跟踪能力。

2 迟滞效应原理

2.1 迟滞效应

迟滞现象广泛存在于以PEA 为驱动的机构中，由于逆压电效应，PEA 升压曲线和降压曲线之间存在回差，最终表现为输入和输出之间存在严重的非线性效应。对于压电式快速反射镜，迟滞效应表现为输入的控制电压信号与镜面偏转角度之间的非线性、多值性和非单一路径的特点。除此之外，PEA 的迟滞特性还与控制信号的频率与幅值有关，呈现为率相关性。

图1 为基于某型号压电式快速反射镜测量的迟滞曲线。图1（a）展示了输入信号幅值一定，不同频率下的迟滞曲线。图1（b）展示了输入信号频率一定，不同幅值下的迟滞曲线。由测试结果可知：输入幅值相同频率变化的电压信号后，输出的迟滞曲线在高频率电压驱动下变宽，输出位移范围减小，并且产生顺时针旋转；输入频率相同幅值变化的电压信号后，输出的迟滞曲线在高幅值电压驱动下变宽，输出位移范围增大，并出现非单调响应现象。

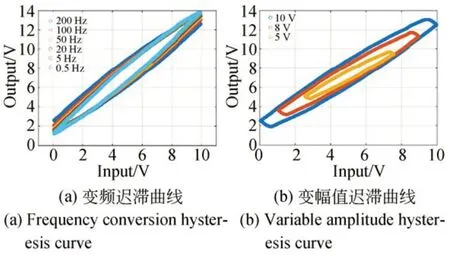
图1 不同输入电压频率和幅值下的迟滞曲线Fig.1 Hysteresis curves at different input voltages and frequencies

2.2 基于Play 算子的P-I 模型

P-I 模型属于唯象模型，是依靠系统的输入输出关系进行建模，核心方法是基于迟滞单元（例如Play、Stop 算子）的加权叠加。本文基于Play 算子建立模拟迟滞特性的P-I 模型。Play 算子的输入信号x和输出信号y之间的关系如图2所示。

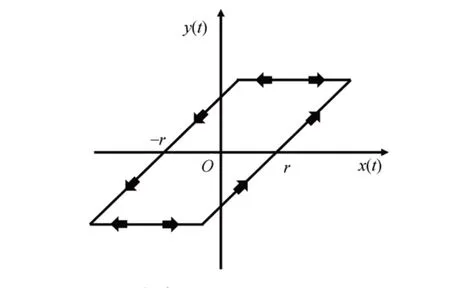
图2 Play 算子Fig.2 Play operator

Play 算子的数学表达式为：

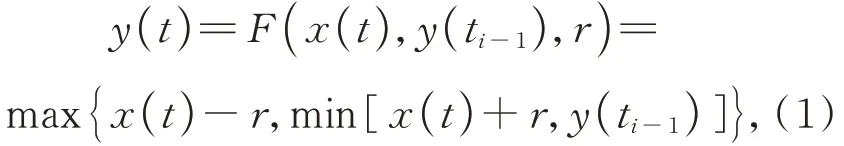
式 中：t∈[t0，tm]，t0≤t0≤…ti-1≤t≤ti≤…≤tm-1≤tm；x(t)为分段单调输入信号。

初始条件为：

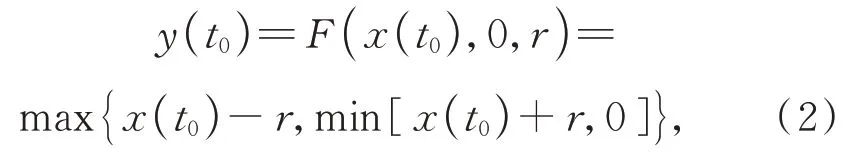
其中r为Play 算子阈值。

将多个阈值不同的Play 算子线性加权叠加，得到具有迟滞特性的模型，输出公式为：

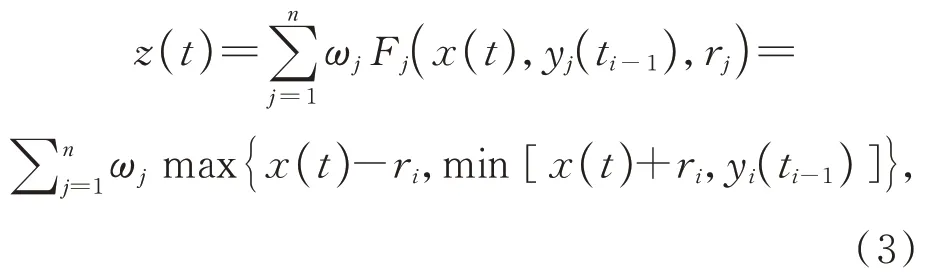
式中：ωj和rj为Play 算子的权重和阈值，满足0=r1＜…＜rn＜+∞；n为play 算 子 加 权 叠 加 的数量。

基于式（1）～式（3）建立迟滞模型并进行仿真分析，如图3 所示。输入随机的正弦信号，输入信号经P-I 模型后输入-输出之间呈现迟滞非线性关系。从图3 可以看出，P-I 模型描述的迟滞曲线受到输入幅值变化的影响，即输入幅值越大，产生的迟滞曲线越宽，该现象与实验测试出的PEA 迟滞特性相符，因此通过合适的方法调整P-I 模型中的权重系数和阈值系数，可以描述实际的PEA 迟滞曲线，以便对迟滞带来的非线性误差进行补偿和抑制。

图3 P-I 模型模拟迟滞特性Fig.3 P-I model simulates hysteresis characteristics

该模型属于静态非线性模型，而实际PEA的迟滞特性是率相关的，迟滞特性不仅受信号幅值的影响，也受信号频率的影响。对于目标变化速率快的动态光学目标跟踪系统，压电式快速反射镜的控制信号频率也快速变化，因此，有必要在此基础上建立一个与输入信号频率相关的动态迟滞模型。

2.3 基于P-I 的率相关模型

为了建立压电式快速反射镜的率相关模型，本文采用Hammerstein 结构将静态非线性P-I 模型与动态线性ARX 模型串联，其结构如图4 所示。图中，u表示输入信号，x表示输入信号经过P-I 模型后的中间信号，y为输出信号。

图4 率相关P-I 模型结构Fig.4 Structure of rate-dependent P-I model

ARX 模型的表达式为：

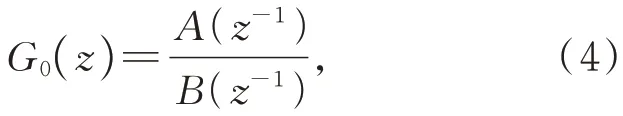
其 中：B(z-1)=b0+b1z-1+b2z-2+…+bnb z-nb，A(z-1)=a0+a1z-1+a2z-2+…+ana z-na。

图5 为基于P-I 的率相关模型在输入相同幅值，不同频率信号下的输出迟滞曲线。该曲线与实际PEA 在不同输入频率信号下的迟滞曲线相同，由此可见，基于P-I 的率相关模型与实际PEA的迟滞特性相符合。

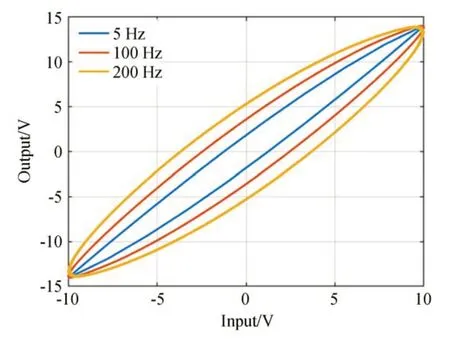
图5 不同输入频率下的率相关P-I 模型输出Fig.5 Rate-dependent P-I model output at different input frequencies

3 迟滞效应补偿

3.1 基于逆模型的前馈控制补偿

为了减小PEA 迟滞非线性的影响，前馈控制是有效的方法之一。本文采用的方法是对上一节建立的迟滞非线性模型求取逆模型，将逆模型作为前馈控制器与压电式快速反射镜串联，补偿PEA 迟滞特性带来的非线性误差，其结构如图6 所示。图中，u表示输入信号，x表示输入信号经过前馈控制器后的中间信号，y为输出信号。

图6 逆模型前馈补偿控制框图Fig.6 Block diagram of inverse model feedforward compensation control

迟滞模型与其逆模型的关系如图7 所示，迟滞逆模型也属于非线性模型，并在坐标系中与迟滞模型关于45°线对称。因此，输入信号经过逆模型计算后再提供给压电式快速反射镜，整个系统的输入信号与输出信号呈线性关系。

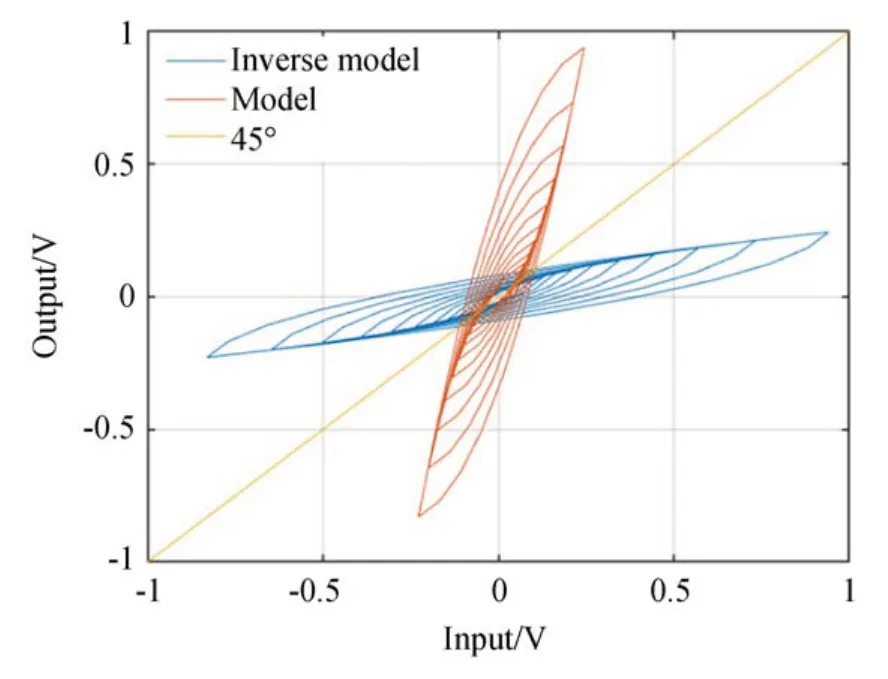
图7 迟滞模型和逆模型示意图Fig.7 Hysteresis model and inverse model

针对动态目标跟踪系统的高频输入信号，本文建立了静态非线性P-I 模型与动态线性ARX模型串联的率相关模型。首先对静态非线性P-I模型取逆，其逆模型可以表示为：

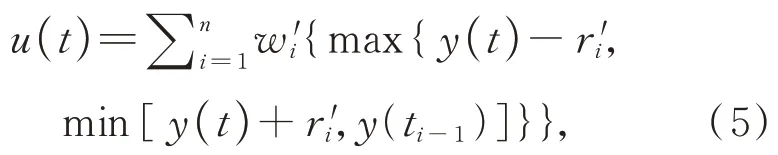
式中：

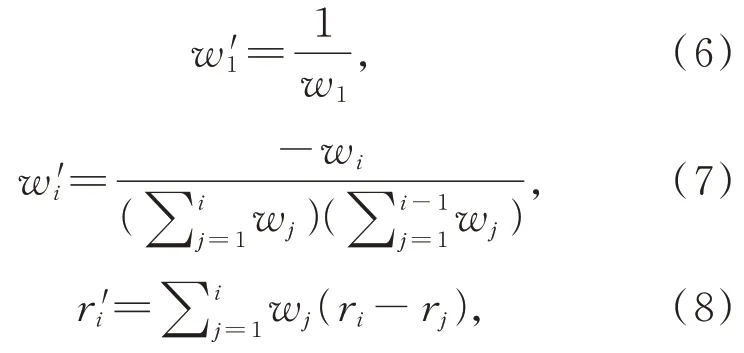
其中w'i和r'i为P-I 逆模型的权重系数和阈值系数。

然后，建立动态线性部分G0(z)的逆模型W0(z)，表示为：

将上述两逆模型串联后得到系统的前馈控制器，前馈控制属于开环控制，其抗干扰能力和稳定性较差。为提高实际工程应用的可靠性，针对存在外界扰动的动态目标跟踪系统，应采用前馈控制与反馈结合的复合控制方式。

3.2 前馈-反馈复合控制补偿

前馈-反馈复合控制结构如图8 所示。图中，u表示控制系统的输入信号，y表示输出信号。前馈控制器为率相关迟滞模型的逆模型，反馈控制器采用PID 控制，其表达式为：

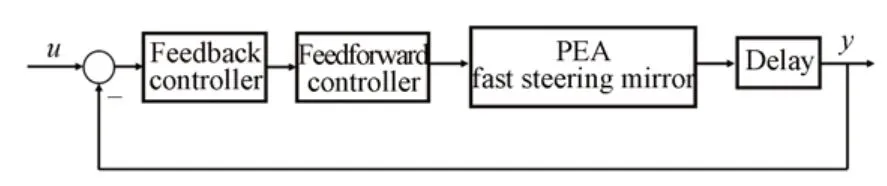
图8 前馈-反馈复合控制框图Fig.8 Block diagram of feedforward-feedback composite control

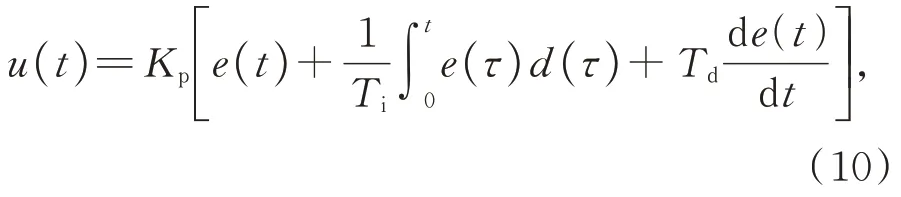
其中：e(t)为参考输入与实际输出的误差；Kp为比例系数；Td为微分时间常数；Ti为积分时间常数。

这种前馈-反馈复合控制结合了前馈控制对迟滞非线性的补偿和反馈控制抗干扰性高、稳定性好的优点，适用于存在外界干扰，且跟踪信号频率较快的动态目标跟踪系统。

3.3 动态目标跟踪性能仿真

基于精跟踪控制系统结构，搭建动态目标跟踪仿真系统，利用基于P-I 的率相关模型表示压电式快速反射镜，用其逆模型作为前馈控制器，PID 作为反馈控制器。

为了探究迟滞补偿对闭环控制系统性能的影响，本文进行了3 种不同控制策略的对比仿真，3 种PID 控制器的参数调节判断条件一致，具体参数如下：

（1）PID 闭环负反馈控制：PID 控制器参数为Kp=0.25，Ti=463.2，Td=0.00026；

（2）基于P-I 模型的前馈补偿结合PID 负反馈的复合控制：PID 控制器参数为Kp=0.27，Ti=501.3，Td=0.000 51；

（3）基于P-I 的率相关动态模型的前馈补偿结合PID 负反馈的复合控制：PID 控制器参数为Kp=0.33，Ti=551.7，Td=0.000 48；

为研究不同控制方式的动态目标跟踪效果，并验证基于率相关动态模型的前馈-反馈复合控制法对动态目标跟踪系统的带宽优化作用，在仿真分析中，通过引入频率从1～500 Hz 递增，幅值指数衰减的正弦信号来模拟跟踪目标的高速变频、变幅运动，分别分析了以上3 种控制方式的误差抑制能力，结果如图9～图10 所示。

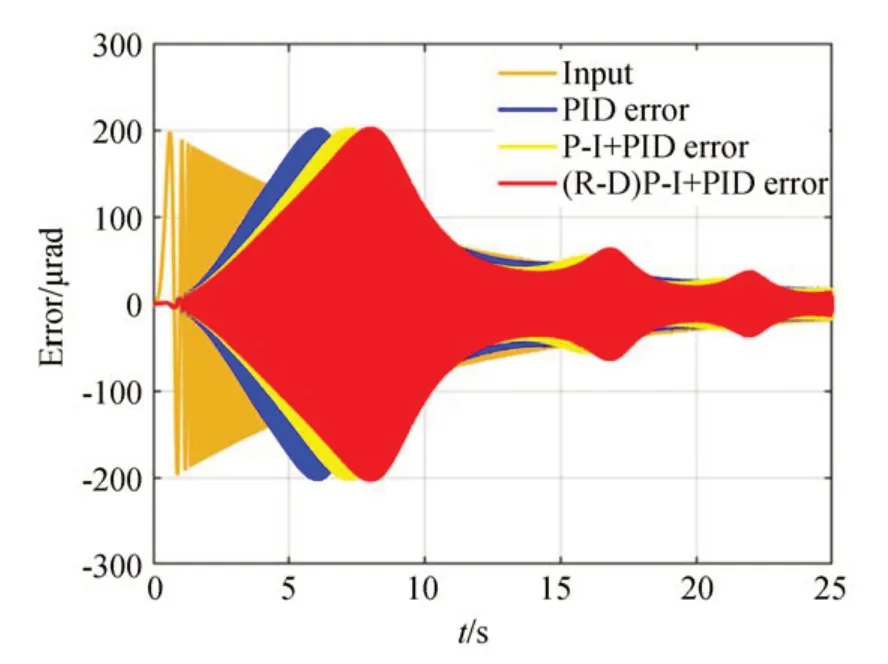
图9 三种控制方式的时域控制效果对比Fig.9 Comparison of time domain control effects of three control modes

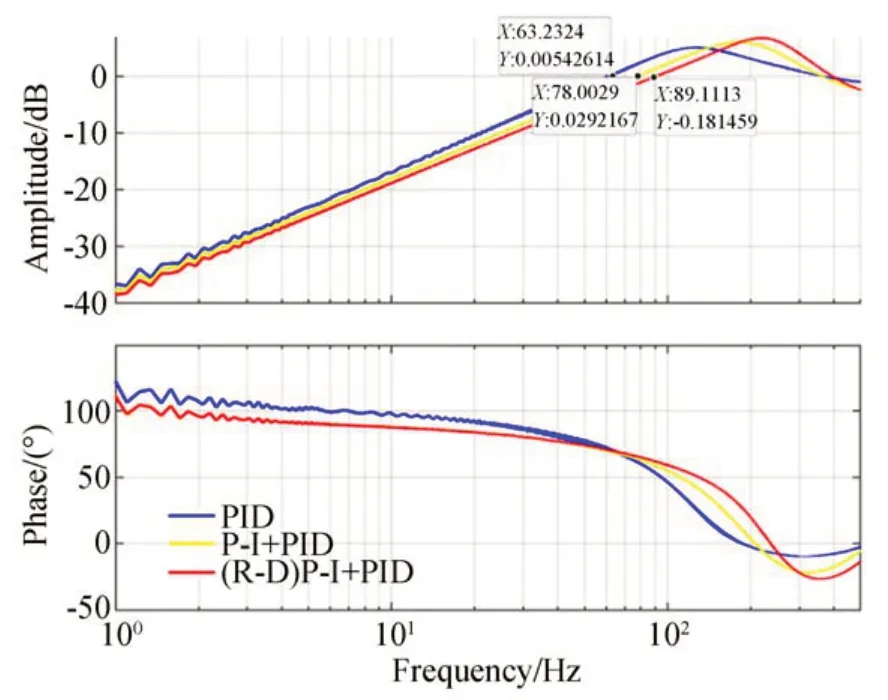
图10 三种控制方式的频域控制效果对比Fig.10 Comparison of frequency domain control effect of three control modes

由仿真结果可知，采用单一PID 负反馈控制系统误差抑制带宽可以达到63 Hz，加入基于P-I 的前馈补偿可以使误差抑制带宽达到78 Hz，在此基础上采用基于P-I 的率相关前馈补偿，可以使系统误差抑制带宽提升到89 Hz。仿真结果表明，前馈补偿可以有效提高压电式快速反射镜跟踪控制系统的性能。对于控制信号幅度、频率快速变化的动态目标跟踪系统，基于率相关的前馈补偿法对系统带宽提高的效果更明显。

4 实验与结果

4.1 实验平台

快速反射镜控制系统实验平台如图11 所示。以嵌入式数字信号处理器作为主控单元，高速相机作为快速反射镜输出偏转量的测量单元，利用快速反射镜1 和快速反射镜2 模拟跟踪目标在方位和俯仰方向的高速运动，以压电式快速反射镜为控制对象进行目标跟踪。

图11 快速反射镜控制系统实验平台Fig.11 Experiment platform of fast steering mirror control system

4.2 迟滞模型辨识与测试

由实验结果可知，压电式快速反射镜在输入电压信号频率较低时（一般在5 Hz 以下），输出的迟滞曲线几乎没有任何变化，近似为静态迟滞系统。因此，本文在低频段辨识压电式快速反射镜模型中的静态非线性部分。采用10 个play 算子来拟合迟滞曲线，权重系数w和阈值系数r的拟合结果如下：

图12 为输入信号为5 Hz 时，P-I模型输出的迟滞曲线与压电式快速反射镜实测的迟滞曲线。可以看到，模型拟合的曲线与实验测量的曲线基本重合，证明静态非线性部分的建模结果良好。

图12 5 Hz 下模型与实测迟滞曲线Fig.12 Model and measured hysteresis curves at 5 Hz

然后，采用宽频谱范围的正弦信号分别激励静态非线性模型和压电式快速反射镜，输出结果分别作为输入和输出数据。将输入输出数据通过系统辨识的方法得到ARX 模型中的参数，从而得到压电式快速反射镜模型中的动态线性部分。辨识结果如下：

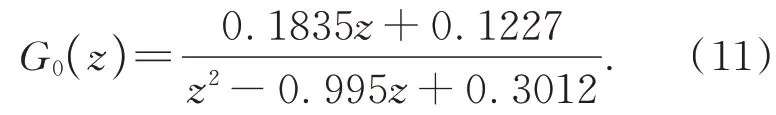
图13 为输入信号为中高频时，基于P-I 的率相关模型输出的迟滞曲线与压电式快速反射镜实测的迟滞曲线。两条曲线一致性好。因此，本文建立的基于P-I 的率相关模型无论在低频段还是高频段都能模拟实际压电式快速反射镜的迟滞非线性曲线。在该参数下求取其逆模型，完成前馈控制器设计。

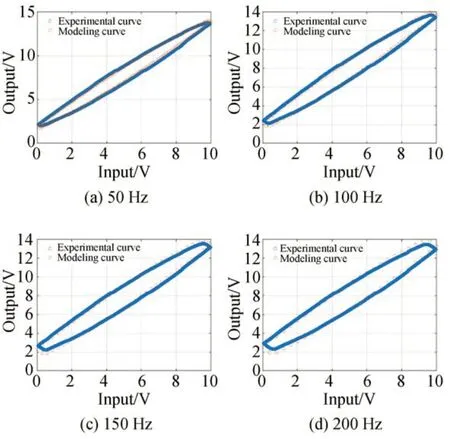
图13 高频段模型与实测迟滞曲线Fig.13 High band model and measured hysteresis curves

4.3 迟滞补偿下的动态目标跟踪

基于本文搭建的动态目标跟踪实验系统，对迟滞前馈补偿效果进行了实验验证。实验中，分别记录了开环、无前馈补偿的闭环PID 控制、基于P-I 模型的静态前馈补偿的闭环PID 控制以及基于P-I 率相关模型的闭环PID 控制条件下的探测器脱靶量，并对其进行了功率谱密度（power spectral density，PSD）分析，结果如图14 所示。

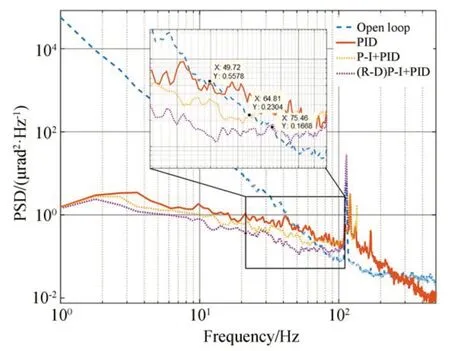
图14 动态目标跟踪实验结果Fig.14 Dynamic target tracking experimental results

由实验结果可知，单一采用PID 负反馈控制时，系统误差功率普密度在49 Hz 之前有抑制效果，在49 Hz 后对误差有放大，起不到抑制效果，因此，该控制方式的误差抑制带宽为49 Hz。通过加入基于P-I 模型的静态迟滞前馈补偿，系统误差抑制带宽从49 Hz 提升到65 Hz，在将迟滞补偿模型更换为率相关动态模型后，系统误差抑制带宽提升到了75 Hz。受实验条件、信号延迟等因素的干扰，实验测试的系统误差抑制带宽与仿真结果相比有所降低，但迟滞补偿带来的系统带宽提升现象与仿真结果一致。实验结果表明，有效抑制压电式快速反射镜的迟滞非线性扰动，可以提高跟踪系统的带宽。

5 结 论

本文根据动态目标跟踪系统带宽需求高、控制信号变化速率快的要求，提出了基于P-I 率相关模型的前馈-反馈复合控制方法。基于P-I 模型模拟迟滞非线性的原理，建立了P-I 模型与ARX 模型串联的率相关迟滞模型。然后，基于实测压电式快速反射镜的数据辨识出了率相关模型的参数，并根据其逆模型设计了补偿迟滞的前馈控制器。最后，搭建了动态目标跟踪实验平台，验证了率相关迟滞模型与压电式快速反射镜实测迟滞曲线的拟合效果，并检验了迟滞补偿方法对动态目标跟踪系统的优化作用。实验结果显示：对于200 Hz 以内的典型信号频率，率相关迟滞模型均能与实测数据较好的拟合；采用基于