具有双接种的病毒变异传染病模型稳定性分析
高文哲,雒志学
(兰州交通大学 数理学院, 兰州 730070)
0 引言
长期以来,传染病都是危害人类健康的最大敌人,人们在努力战胜它的过程中,已取得了显著的成果[1-5]。然而随着疾病的发展,病毒在传播过程中可能会发生变异,从而导致疾病失控。梁桂珍等[6]、渠亚娇等[7]和李冬梅等[8]研究了具有病毒变异的传染病模型,讨论了疾病流行的阈值和系统各个平衡点的稳定性;Cai等[9-10]对具有接种的病毒变异传染病模型进行了稳定性分析,但只考虑了接种个体对其中某一阶段的病毒完全有效的情况;Baba等[11-12]考虑了对2种病毒分别有阻碍作用的双接种传染病问题,却并未考虑感染这2种病毒的患者之间会发生转换的情况。因此在病毒变异传染病问题的研究基础上,考虑对易感人群进行2种疫苗接种的情况,提出一类具有双接种的病毒变异传染病模型。
1 模型建立
本节考虑疫苗接种对预防传染病发生的重要作用,引入一类具有双接种的病毒变异传染病模型。假设第一种疫苗接种者对变异前病毒完全免疫而对变异后病毒有部分抵抗作用,第二种疫苗接种者对变异后病毒完全免疫而对变异前病毒有部分抵抗作用,2类感染者都具有传染性,且病毒变异前该疾病不足以致命,而病毒变异后该疾病足以致命。基于以上假设,建立如下模型:
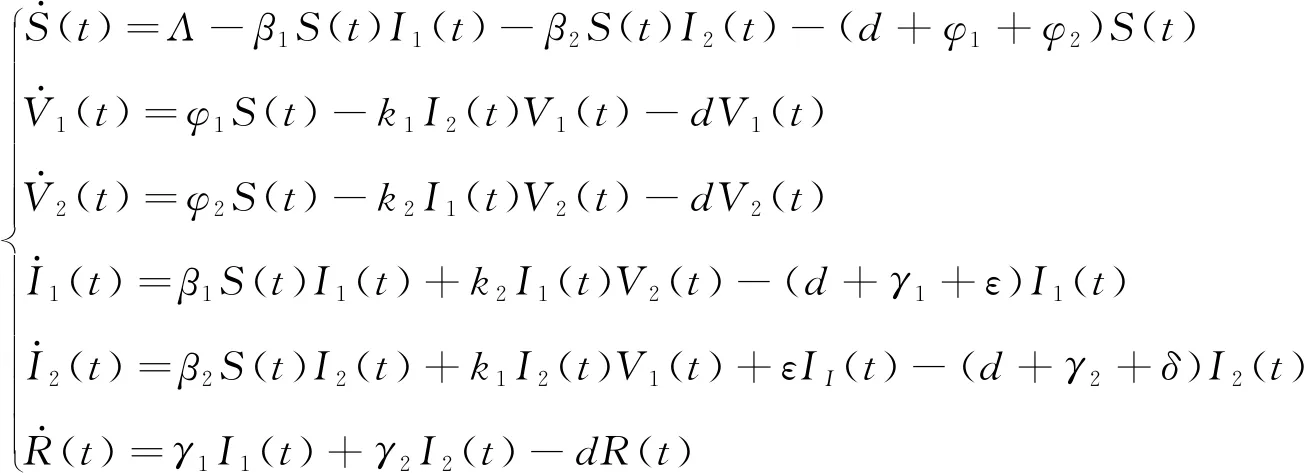
(1)
式中:S(t),V1(t),V2(t),I1(t),I2(t),R(t)分别表示t时刻易感染者,第一种疫苗接种者,第二种疫苗接种者,病毒变异前感染者,病毒变异后感染者和恢复者的数量;Λ表示种群的输入率;β1,β2分别表示病毒变异前后感染者对易感人群的传染系数;d表示种群的自然死亡率;φ1,φ2表示第一种疫苗与第二种疫苗的接种率;k2表示病毒变异前感染者对第二种疫苗接种者的传染率;k1表示病毒变异后感染者对第一种疫苗接种者的传染率;γ1和γ2分别表示病毒变异前后感染者的恢复率;ε表示病毒变异前感染者转换为病毒变异后感染者的速率;δ表示病毒变异后感染者的因病死亡率。根据模型的生物意义,假设所有参数均为正数。
令N(t)=S(t)+V1(t)+V2(t)+I1(t)+I2(t)+R(t),由系统(1)可得
由常微分方程的比较原理知
所以

(2)
因系统(1)的前5个方程中不含变量R,所以只需要考虑如下系统:
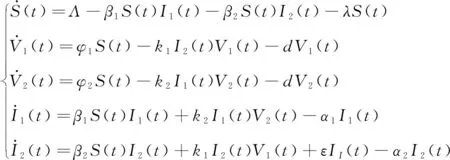
(3)
式中:λ=d+φ1+φ2,α1=d+γ1+ε,α2=d+γ2+δ,记S=S(t),V1=V1(t),V2=V2(t),I1=I1(t),I2=I2(t)。

2 基本再生数与平衡点的存在性
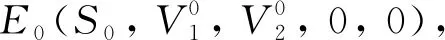
F和V在E0处的Jacobi矩阵为:
因此
则定义基本再生数表达式:
R0=ρ(FV-1)=max{R1,R2}

以下将对系统(3)各平衡点的存在性进行讨论。

证明系统(3)的平衡点满足如下方程:

(4)

当I1=0,I2≠0时,由方程组(4)的前3个式子可得

(5)
式中:
a1=α2k1β2,a2=α2dβ2+α2λk1-β2k1Λ,a3=α2dλ-k1φ1Λ-β2dΛ
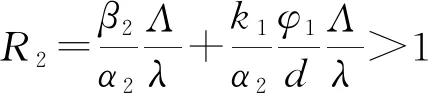

当I1I2≠0时,由方程组(4)的前3个式子可得
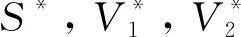

式中:a1=α1β1k2,b1=α1β2k2,d1=α1β1d+α1k2λ-β2k2Λ,f1=α1β2d,g1=α1λd-β1Λd-k2φ2Λ,a2=-α2β2k1,b2=β1εk1-α2β1k1,c2=β1εk1,d2=β1dε,e2=β2Λk1-α2β2d-α2λk1,f2=ελk1+β2dε-α2β1d,g2=εdλ,h=β2Λd+k1φ1Λ-α2dλ。

3 局部稳定性分析
下面通过Jacobi矩阵与Hurwitz判别法证明无病平衡点和边界平衡点的局部渐近稳定性,系统(3)在任意点E(S,V1,V2,I1,I2)处的Jacobi矩阵为:
(6)
式中:M=-β1I1-β2I2-λ,N=β1S+k2V2-α1,Q=β2S+k1V1-α2。

证明由式(6)知,系统(3)在点E0处的Jacobi矩阵为:
特征方程为:
显然
故当R1<1且R2<1时,特征根均为负实数,即当R0=max{R1,R2}<1时,无病平衡点E0局部渐近稳定。
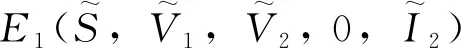
证明系统(3)在点E1处的特征方程为:
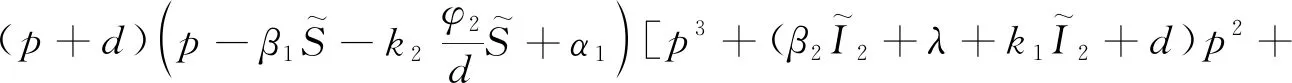
(7)
显然
特征根p3,p4,p5由如下多项式所确定:
p3+a1p2+a2p+a3=0
式中:
显然
式中:
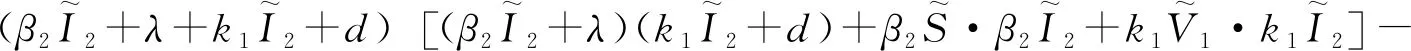

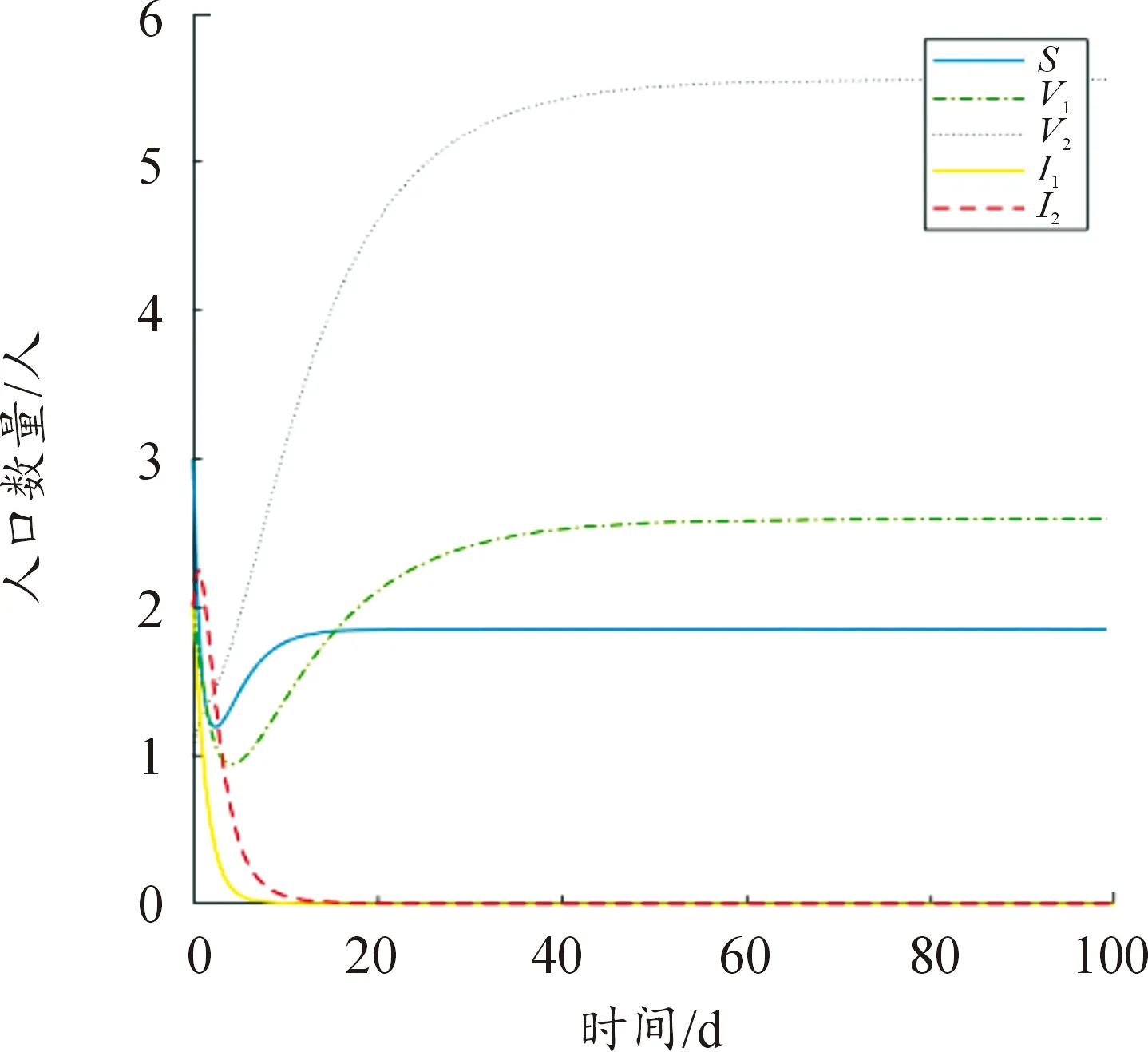
利用Hurwitz判别法可知当R1<1 本节将通过构造Lyapunov函数并借助LaSalle不变集原理对系统(3)的2个平衡点E0和E1的全局渐近稳定性进行分析。 证明由于R0=max{R1,R2}<1意味着R1<1,所以由方程组(3)的4个等式知 (8) 当t→∞时,I1(t)→0。 故在I1(t)=0的平面上,构造如下Lyapunov函数: 沿着系统(3)的轨迹对函数V(t)进行求导: 由算数平均数与几何平均数知 当R2<1时, 式中: 对函数V(t)沿着系统(3)的轨迹求导: 由算数平均数与几何平均数知 由于边界平衡点E1满足方程组(4),经计算可知 下面将给出2个数值模拟。 取系统(3)中的参数Λ=1,d=0.1,β1=0.15,β2=0.18,γ1=0.48,γ2=0.45,φ1=0.14,φ2=0.3,ε=0.54,δ=0.4,k1=0.16,k2=0.14,S(0)=3,V1(0)=2,V2(0)=1,I1(0)=2,I2(0)=2。经计算R1=0.942 5,R2=0.787 5,由定理4知无病平衡E0是全局渐近稳定的,其数值模拟如图1所示。 图1 无病平衡点E0的全局渐近稳定性 取系统(3)中的参数Λ=1,d=0.1,β1=0.15,β2=0.22,γ1=0.35,γ2=0.25,φ1=0.5,φ2=0.4,ε=0.54,δ=0.2,k1=0.24,k2=0.15,S(0)=3,V1(0)=2,V2(0)=1,I1(0)=2,I2(0)=2。经计算R1=0.757 6,R2=2.581 8,由定理5知边界平衡点E1是全局渐近稳定的,其数值模拟如图2所示。4 全局稳定性分析




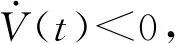
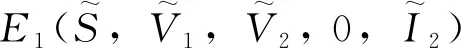
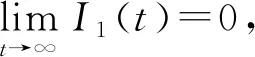

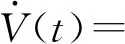
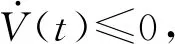
5 数值模拟
6 结论


